4.5: Resolva sistemas de equações com três variáveis
- Page ID
- 183201
Ao final desta seção, você poderá:
- Determine se um triplo ordenado é uma solução de um sistema de três equações lineares com três variáveis
- Resolva um sistema de equações lineares com três variáveis
- Resolva aplicações usando sistemas de equações lineares com três variáveis
Antes de começar, faça este teste de prontidão.
- Avalie\(5x−2y+3z\) quando\(x=−2, y=−4,\) e\(z=3.\)
se você perdeu esse problema, revise [link]. - Classifique as equações como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução. \( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
Se você perdeu esse problema, revise [link]. - Classifique as equações como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução. \(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right. \)
Se você perdeu esse problema, revise [link].
Determine se um triplo ordenado é uma solução de um sistema de três equações lineares com três variáveis
Nesta seção, estenderemos nosso trabalho de resolução de um sistema de equações lineares. Até agora, trabalhamos com sistemas de equações com duas equações e duas variáveis. Agora vamos trabalhar com sistemas de três equações com três variáveis. Mas primeiro vamos revisar o que já sabemos sobre a solução de equações e sistemas envolvendo até duas variáveis.
Aprendemos anteriormente que o gráfico de uma equação linear,\(ax+by=c\), é uma linha. Cada ponto na linha, um par ordenado\((x,y)\), é uma solução para a equação. Para um sistema de duas equações com duas variáveis, representamos graficamente duas linhas. Então, podemos ver que todos os pontos que são soluções para cada equação formam uma linha. E, ao descobrir o que as linhas têm em comum, encontraremos a solução para o sistema.
A maioria das equações lineares em uma variável tem uma solução, mas vimos que algumas equações, chamadas contradições, não têm soluções e para outras equações, chamadas identidades, todos os números são soluções
Sabemos que quando resolvemos um sistema de duas equações lineares representadas por um gráfico de duas retas no mesmo plano, há três casos possíveis, conforme mostrado.
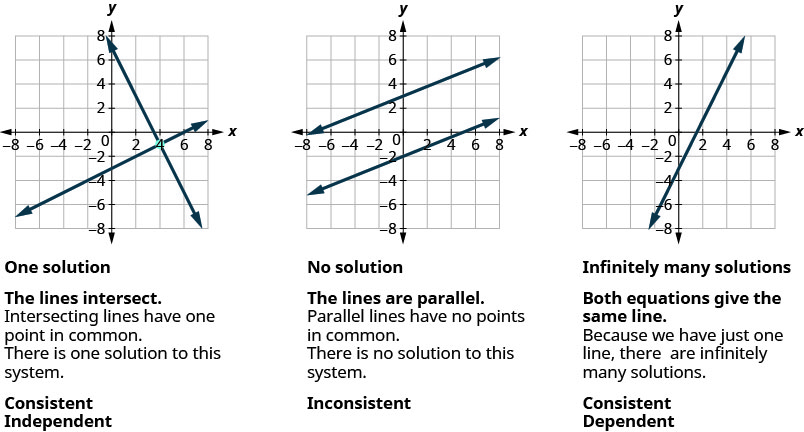
Da mesma forma, para uma equação linear com três variáveis ax+by+cz=d, ax+by+cz=d, cada solução da equação é uma tripla ordenada (x, y, z) (x, y, z) que torna a equação verdadeira.
Uma equação linear com três variáveis, onde a, b, c e d são números reais e a, b e c não são todos 0, tem a forma
\[ ax+by+cz=d\nonumber \]
Cada solução para a equação é uma tripla ordenada, o\((x,y,z)\) que torna a equação verdadeira.
Todos os pontos que são soluções para uma equação formam um plano no espaço tridimensional. E, ao descobrir o que os aviões têm em comum, encontraremos a solução para o sistema.
Quando resolvemos um sistema de três equações lineares representadas por um gráfico de três planos no espaço, há três casos possíveis.

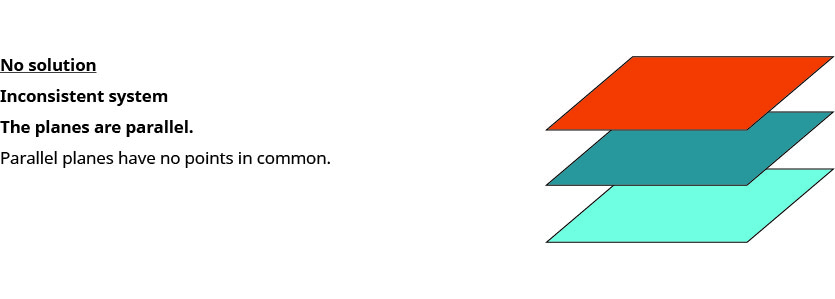






Para resolver um sistema de três equações lineares, queremos encontrar os valores das variáveis que são soluções para todas as três equações. Em outras palavras, estamos procurando o triplo ordenado\((x,y,z)\) que torna todas as três equações verdadeiras. Essas são chamadas de soluções do sistema de três equações lineares com três variáveis.
As soluções de um sistema de equações são os valores das variáveis que tornam todas as equações verdadeiras. Uma solução é representada por um triplo ordenado\((x,y,z)\).
Para determinar se um triplo ordenado é uma solução para um sistema de três equações, substituímos os valores das variáveis em cada equação. Se o triplo ordenado tornar todas as três equações verdadeiras, é uma solução para o sistema.
Determine se o triplo solicitado é uma solução para o sistema:\( \left\{ \begin{array} {l} x−y+z=2 \\ 2x−y−z=−6 \\ 2x+2y+z=−3 \end{array} \right. \)
ⓐ\((−2,−1,3)\) ⓑ\((−4,−3,4)\)
- Responda
-
ⓐ
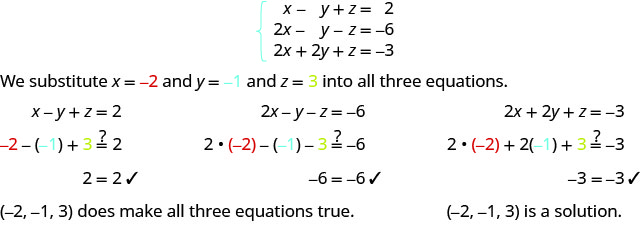
ⓑ
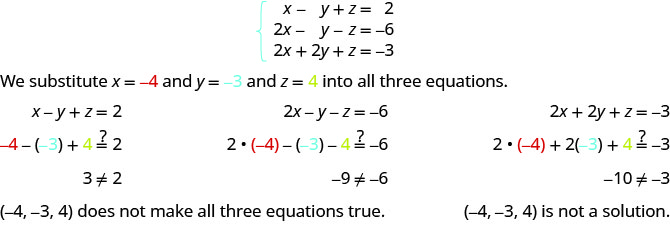
Determine se o triplo solicitado é uma solução para o sistema:\( \left\{ \begin{array} {l} 3x+y+z=2 \\ x+2y+z=−3 \\ 3x+y+2z=4 \end{array} \right. \)
ⓐ\((1,−3,2)\) ⓑ\((4,−1,−5)\)
- Responda
-
ⓐ sim ⓑ não
Determine se o triplo solicitado é uma solução para o sistema:\( \left\{ \begin{array} {l} x−3y+z=−5 \\ −3x−y−z=1 \\ 2x−2y+3z=1 \end{array} \right. \)
ⓐ\((2,−2,3)\) ⓑ\((−2,2,3)\)
- Responda
-
ⓐ não ⓑ sim
Resolva um sistema de equações lineares com três variáveis
Para resolver um sistema de equações lineares com três variáveis, usamos basicamente as mesmas técnicas que usamos com sistemas que tinham duas variáveis. Começamos com dois pares de equações e em cada par eliminamos a mesma variável. Isso nos dará um sistema de equações com apenas duas variáveis e então saberemos como resolver esse sistema!
Em seguida, usamos os valores das duas variáveis que acabamos de encontrar para voltar à equação original e encontrar a terceira variável. Escrevemos nossa resposta como um triplo ordenado e, em seguida, verificamos nossos resultados.
Resolva o sistema por eliminação:\( \left\{ \begin{array} {l} x−2y+z=3 \\ 2x+y+z=4 \\ 3x+4y+3z=−1 \end{array} \right. \)
- Responda
-






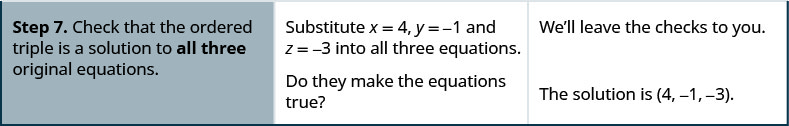
Resolva o sistema por eliminação:\( \left\{ \begin{array} {l} 3x+y−z=2 \\ 2x−3y−2z=1 \\ 4x−y−3z=0 \end{array} \right.\)
- Responda
-
\((2,−1,3)\)
Resolva o sistema por eliminação:\( \left\{ \begin{array} {l} 4x+y+z=−1 \\ −2x−2y+z=2 \\ 2x+3y−z=1 \end{array} \right. \)
- Responda
-
\((−2,3,4)\)
As etapas estão resumidas aqui.
- Escreva as equações na forma padrão
- Se algum coeficiente for fracionário, limpe-o.
- Elimine a mesma variável de duas equações.
- Decida qual variável você eliminará.
- Trabalhe com um par de equações para eliminar a variável escolhida.
- Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
- Adicione as equações resultantes da Etapa 2 para eliminar uma variável
- Repita a Etapa 2 usando duas outras equações e elimine a mesma variável da Etapa 2.
- As duas novas equações formam um sistema de duas equações com duas variáveis. Resolva esse sistema.
- Use os valores das duas variáveis encontradas na Etapa 4 para encontrar a terceira variável.
- Escreva a solução como uma tripla ordenada.
- Verifique se o triplo ordenado é uma solução para todas as três equações originais.
Resolver:\( \left\{ \begin{array} {l} 3x−4z=0 \\ 3y+2z=−3 \\ 2x+3y=−5 \end{array} \right. \)
- Responda
-
\[ \left\{ \begin{array} {ll} 3x−4z=0 &(1) \\ 3y+2z=−3 &(2) \\ 2x+3y=−5 &(3) \end{array} \right. \nonumber \]
Podemos eliminar\(z\) das equações (1) e (2) multiplicando a equação (2) por 2 e depois adicionando as equações resultantes.
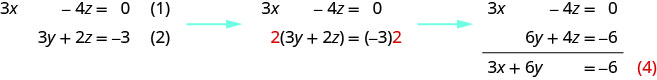
Observe que as equações (3) e (4) têm as variáveis\(x\)\(y\) e. Resolveremos esse novo sistema para\(x\)\(y\) e.
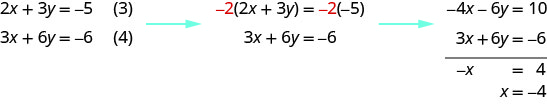
Para resolver y, substituímos\(x=−4\) na equação (3).
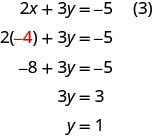
Agora temos\(x=−4\)\(y=1\) e. Precisamos resolver para z. Podemos substituir\(x=−4\) na equação (1) para encontrar z.
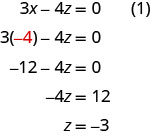
Escrevemos a solução como um triplo ordenado. \((−4,1,−3)\)
Verificamos se a solução torna as três equações verdadeiras.
\(\begin{array} {lll} {3x-4z=0 \space (1)} &{3y+2z=−3 \space (2)} &{2x+3y=−5 \space (3)} \\ {3(−4)−4(−3)\overset{?}{=} 0} &{3(1)+2(−3)\overset{?}{=} −3} &{2(−4)+3(1)\overset{?}{=} −5} \\ {0=0 \checkmark} &{−3=−3 \checkmark} &{−5=−5 \checkmark} \\ {} &{} &{\text{The solution is }(−4,1,−3)} \end{array}\)
Resolver:\( \left\{ \begin{array} {l} 3x−4z=−1 \\ 2y+3z=2 \\ 2x+3y=6 \end{array} \right. \)
- Responda
-
\((−3,4,−2)\)
Resolver:\( \left\{ \begin{array} {l} 4x−3z=−5 \\ 3y+2z=7 \\ 3x+4y=6 \end{array} \right. \)
- Responda
-
\((−2,3,−1)\)
Quando resolvemos um sistema e acabamos sem variáveis e com uma declaração falsa, sabemos que não há soluções e que o sistema é inconsistente. O próximo exemplo mostra um sistema de equações que é inconsistente.
Resolva o sistema de equações:\( \left\{ \begin{array} {l} x+2y−3z=−1 \\ x−3y+z=1 \\ 2x−y−2z=2 \end{array} \right. \)
- Responda
-
\[\left\{ \begin{array} {ll} x+2y−3z=−1 &(1) \\ x−3y+z=1 &(2) \\ 2x−y−2z=2 &(3) \end{array} \right.\nonumber \]
Use as equações (1) e (2) para eliminar z.
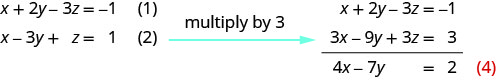
Use (2) e (3) para eliminar\(z\) novamente.
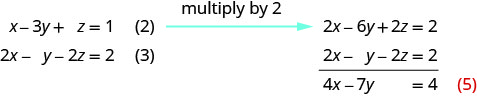
Use (4) e (5) para eliminar uma variável.

Não há solução.
Ficamos com uma declaração falsa e isso nos diz que o sistema é inconsistente e não tem solução.
Resolva o sistema de equações:\( \left\{ \begin{array} {l} x+2y+6z=5 \\ −x+y−2z=3 \\ x−4y−2z=1 \end{array} \right. \)
- Responda
-
sem solução
Resolva o sistema de equações:\( \left\{ \begin{array} {l} 2x−2y+3z=6 \\ 4x−3y+2z=0 \\ −2x+3y−7z=1 \end{array} \right. \)
- Responda
-
sem solução
Quando resolvemos um sistema e acabamos sem variáveis além de uma afirmação verdadeira, sabemos que existem infinitas soluções. O sistema é consistente com as equações dependentes. Nossa solução mostrará como duas das variáveis dependem da terceira.
Resolva o sistema de equações:\( \left\{ \begin{array} {l} x+2y−z=1 \\ 2x+7y+4z=11 \\ x+3y+z=4 \end{array} \right. \)
- Responda
-
\[\left\{ \begin{array} {ll} x+2y−z=1 &(1) \\ 2x+7y+4z=11 &(2) \\ x+3y+z=4 &(3) \end{array} \right.\nonumber \]
Use as equações (1) e (3) para eliminar x.

Use as equações (1) e (2) para eliminar x novamente.
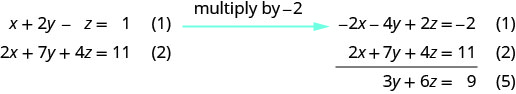
Use as equações (4) e (5) para eliminar\(y\).
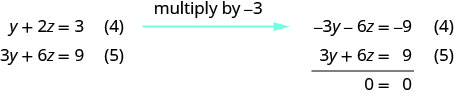
Existem infinitas soluções. Resolva a equação (4) para y. Represente a solução mostrando como x e y dependem de z.
\( \begin{aligned} y+2z &= 3 \\ y &= −2z+3 \end{aligned} \)Use a equação (1) para resolver x. \( x+2y−z=1\) Substituto\(y=−2z+3\). \( \begin{aligned} x+2(−2z+3)−z &= 1 \\ x−4z+6−z &= 1 \\ x−5z+6 &= 1 \\ x &= 5z−5 \end{aligned} \) A afirmação verdadeira nos\(0=0\) diz que esse é um sistema dependente que tem infinitas soluções. As soluções são da forma (x, y, z) (x, y, z) onde\(x=5z−5;\space y=−2z+3\) e z é qualquer número real.
Resolva o sistema por equações:\( \left\{ \begin{array} {l} x+y−z=0 \\ 2x+4y−2z=6 \\ 3x+6y−3z=9 \end{array} \right. \)
- Responda
-
infinitamente muitas soluções\((x,3,z)\) onde\(x=z−3;\space y=3;\space z\) está qualquer número real
Resolva o sistema por equações:\( \left\{ \begin{array} {l} x−y−z=1 \\ −x+2y−3z=−4 \\ 3x−2y−7z=0 \end{array} \right. \)
- Responda
-
infinitamente muitas soluções\((x,y,z)\) onde\(x=5z−2;\space y=4z−3;\space z\) está qualquer número real
Resolva aplicações usando sistemas de equações lineares com três variáveis
As aplicações que são modeladas por um sistema de equações podem ser resolvidas usando as mesmas técnicas que usamos para resolver os sistemas. Muitos dos aplicativos são apenas extensões para três variáveis dos tipos que resolvemos anteriormente.
O departamento de teatro da faculdade comunitária vendeu três tipos de ingressos para sua última produção teatral. Os ingressos para adultos foram vendidos por $15, os ingressos para estudantes por $10 e os ingressos para crianças por $8. O departamento de teatro ficou entusiasmado por ter vendido 250 ingressos e arrecadado $2.825 em uma noite. O número de ingressos para estudantes vendidos é o dobro do número de ingressos para adultos vendidos. Quantos de cada tipo o departamento vendeu?
- Responda
-
Usaremos um gráfico para organizar as informações. 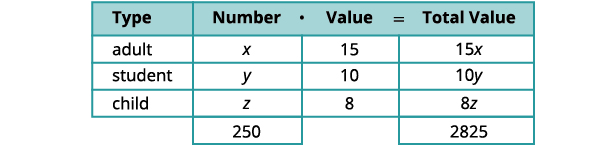
O número de estudantes é o dobro do número de adultos. Reescreva a equação na forma padrão. \(\begin{aligned} y &= 2x \\ 2x−y &= 0 \end{aligned} \) 
Use as equações (1) e (2) para eliminar z. 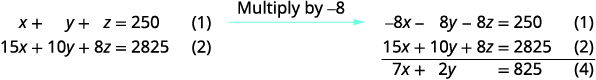
Use (3) e (4) para eliminar\(y\). 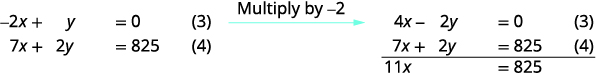
Resolva para x. \(x=75 \)ingressos para adultos Use a equação (3) para encontrar y. \(−2x+y=0\) Substituto\(x=75\). \(\begin{aligned} −2(75)+y &= 0 \\ −150+y &= 0 \\ y &= 150\text{ student tickets}\end{aligned} \) Use a equação (1) para encontrar z. \(x+y+z=250\) Substitua os valores
\(x=75, \space y=150.\)
\(\begin{aligned} 75+150+z &= 250 \\ 225+z &= 250 \\ z &= 25\text{ child tickets} \end{aligned} \)Escreva a solução. O departamento de teatro vendeu 75 ingressos para adultos,
150 ingressos para estudantes e 25 ingressos para crianças.
O departamento de artes plásticas da faculdade comunitária vendeu três tipos de ingressos para sua última apresentação de dança. Os ingressos para adultos foram vendidos por $20, os ingressos para estudantes por $12 e os ingressos para crianças por $10.O departamento de artes plásticas ficou entusiasmado por ter vendido 350 ingressos e arrecadado $4.650 em uma noite. O número de ingressos infantis vendidos é o mesmo que o número de ingressos para adultos vendidos. Quantos de cada tipo o departamento vendeu?
- Responda
-
O departamento de artes plásticas vendeu 75 ingressos para adultos, 200 ingressos para estudantes e 75 ingressos para crianças.
O time de futebol da faculdade comunitária vendeu três tipos de ingressos para seu último jogo. Os ingressos para adultos foram vendidos por $10, os ingressos para estudantes por $8 e os ingressos para crianças por $5. O time de futebol ficou entusiasmado por ter vendido 600 ingressos e arrecadado $4.900 para um jogo. O número de ingressos para adultos é o dobro do número de ingressos infantis. Quantos de cada tipo o time de futebol vendeu?
- Responda
-
O time de futebol vendeu 200 ingressos para adultos, 300 ingressos para estudantes e 100 ingressos para crianças.
Acesse esse recurso on-line para obter instruções e práticas adicionais sobre como resolver um sistema linear em três variáveis sem soluções ou soluções infinitas.
- Resolvendo um sistema linear em três variáveis com soluções inexistentes ou infinitas
- 3 Aplicação variável
Conceitos-chave
- Equação linear em três variáveis: Uma equação linear com três variáveis, onde a, b, c e d são números reais e a, b e c não são todas 0, tem a forma
\[ax+by+cz=d\nonumber \]
Cada solução para a equação é uma tripla ordenada, o\((x,y,z)\) que torna a equação verdadeira. - Como resolver um sistema de equações lineares com três variáveis.
- Escreva as equações na forma padrão
Se algum coeficiente for fracionário, limpe-o. - Elimine a mesma variável de duas equações.
Decida qual variável você eliminará.
Trabalhe com um par de equações para eliminar a variável escolhida.
Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
Adicione as equações resultantes da Etapa 2 para eliminar uma variável - Repita a Etapa 2 usando duas outras equações e elimine a mesma variável da Etapa 2.
- As duas novas equações formam um sistema de duas equações com duas variáveis. Resolva esse sistema.
- Use os valores das duas variáveis encontradas na Etapa 4 para encontrar a terceira variável.
- Escreva a solução como uma tripla ordenada.
- Verifique se o triplo ordenado é uma solução para todas as três equações originais.
- Escreva as equações na forma padrão
Glossário
- soluções de um sistema de equações lineares com três variáveis
- As soluções de um sistema de equações são os valores das variáveis que tornam todas as equações verdadeiras; uma solução é representada por um triplo ordenado (x, y, z).


