Skip to main content
Global

4.4E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183186

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Resolver aplicações de mistura

    Nos exercícios a seguir, traduza para um sistema de equações e resolva.

    1. Os ingressos para um show da Broadway custam $35 para adultos e $15 para crianças. O total de receitas de 1650 ingressos em uma apresentação foi de $47.150. Quantos ingressos para adultos e quantos ingressos para crianças foram vendidos?

    2. Os ingressos para o show do Cirque du Soleil custam $70 para adultos e $50 para crianças. Uma apresentação noturna teve um total de 300 ingressos vendidos e as receitas totalizaram $17.200. Quantos ingressos para adultos e quantos ingressos para crianças foram vendidos?

    Responda

    110 ingressos para adultos, 190 ingressos para crianças

    3. Os ingressos para um trem da Amtrak custam $10 para crianças e $22 para adultos. Josie pagou $1200 por um total de 72 ingressos. Quantos ingressos para crianças e quantos ingressos para adultos Josie comprou?

    4. Os ingressos para um jogo de beisebol do Minnesota Twins custam $69 para assentos no nível principal e $39 para assentos no nível do terraço. Um grupo de dezesseis amigos foi ao jogo e gastou um total de $804 para comprar os ingressos. Quantos ingressos para o Main Level e quantos ingressos para o Terrace Level eles compraram?

    Responda

    6 assentos bons, 10 assentos baratos

    5. Os ingressos para um recital de dança custam $15 para adultos e $7 dólares para crianças. A companhia de dança vendeu 253 ingressos e as receitas totais foram de $2771. Quantos ingressos para adultos e quantos ingressos para crianças foram vendidos?

    6. Os ingressos para a feira comunitária custam $12 para adultos e $5 dólares para crianças. No primeiro dia da feira, 312 ingressos foram vendidos por um total de $2204. Quantos ingressos para adultos e quantos ingressos para crianças foram vendidos?

    Responda

    92 ingressos para adultos, 220 ingressos para crianças

    7. Brandon tem uma xícara de moedas e moedas de dez centavos com um valor total de\($3.80\). O número de trimestres é quatro a menos que o dobro do número de trimestres. Quantos quartos e quantos centavos Brandon tem?

    8. Sherri economiza moedas e moedas de dez centavos em uma bolsa de moedas para sua filha. O valor total das moedas na bolsa é\($0.95\). O número de níquel é dois a menos de cinco vezes o número de moedas de dez centavos. Quantos centavos e quantas moedas de dez centavos estão na bolsa de moedas?

    Responda

    13 níqueis, 3 moedas de dez centavos

    9. Peter está guardando seus trocos há vários dias. Quando ele contou seus quartos e moedas, ele descobriu que eles tinham um valor total\($13.10\). O número de trimestres foi quinze a mais do que três vezes o número de moedas de dez centavos. Quantos quartos e quantos centavos Peter tinha?

    10. Lucinda tinha um bolso cheio de moedas de dez centavos e moedas com um valor de\($6.20\). O número de moedas de dez centavos é dezoito a mais do que três vezes o número de trimestres. Quantos centavos e quantos quartos Lucinda tem?

    Responda

    42 centavos, 8 quartos

    11. Um caixa tem 30 notas, todas de $10 ou $20. O valor total do dinheiro é de $460. Quantos de cada tipo de fatura o caixa tem?

    12. Um caixa tem 54 notas, todas de $10 ou $20. O valor total do dinheiro é de $910. Quantos de cada tipo de fatura o caixa tem?

    Responda

    17 notas de $10, 37 notas de $20

    13. Marissa quer misturar doces vendidos\($1.80\) por quilo com doces custando\($1.20\) por quilo para obter uma mistura que custa\($1.40\) por quilo para fazer. Ela quer fazer 90 libras da mistura de doces. Quantos quilos de cada tipo de doce ela deve usar?

    14. Quantas libras de nozes vendidas por $6 por libra e passas vendidas por $3 por libra Kurt deve combinar para obter 120 libras de mix de trilha que lhe custou $5 por libra?

    Responda

    80 libras de nozes e 40 libras de passas

    15. Hannah tem que ganhar vinte e cinco galões de ponche para uma festa. O ponche é feito de refrigerante e suco de frutas. O custo do refrigerante é\($1.79\) por galão e o custo da bebida de frutas é\($2.49\) por galão. O orçamento de Hannah exige que o ponche custe\($2.21\) por galão. Quantos galões de refrigerante e quantos galões de suco de fruta ela precisa?

    16. Joseph gostaria de fazer doze libras de uma mistura de café a um custo de $6 por libra. Ele mistura chicória moída a $5 a libra com a Jamaican Blue Mountain a $9 por libra. Quanto de cada tipo de café ele deve usar?

    Responda

    9 libras de café de chicória, 3 libras de café jamaicano Blue Mountain

    17. Julia e seu marido são donos de uma cafeteria. Eles experimentaram misturar um café colombiano City Roast que custava $7,80 por libra com café colombiano torrado francês que custava $8,10 por libra para fazer uma mistura de vinte libras. Sua mistura deve custar-lhes $7,92 por libra. Quanto de cada tipo de café eles devem comprar?

    18. Melody, de 12 anos, quer vender sacos de doces mistos em sua barraca de limonada. Ela misturará M&M's que custam $4,89 por sacola e Reese's Pieces que custam $3,79 por sacola para obter um total de vinte e cinco sacos de doces mistos. Melody quer que os sacos de doces mistos lhe custem $4,23 por saco para fazer. Quantas sacolas de M&M e quantas sacolas de Reese's Pieces ela deve usar?

    Responda

    10 sacos de M&M's, 15 sacos de Reese's Pieces

    19. Jotham precisa de 70 litros de uma solução de 50% de uma solução alcoólica. Ele tem uma solução de 30% e 80% disponível. Quantos litros das soluções de 30% e quantos litros das soluções de 80% ele deve misturar para fazer a solução de 50%?

    20. Joy está preparando 15 litros de uma solução salina de 25%. Ela só tem 40% e 10% de solução em seu laboratório. Quantos litros dos 40% e quantos litros dos 10% ela deve misturar para fazer a solução de 25%?

    Responda

    \(7.5\)litros de cada solução

    21. Um cientista precisa de 65 litros de uma solução com 15% de álcool. Ela tem uma solução disponível de 25% e 12%. Quantos litros das soluções de 25% e quantos litros das soluções de 12% ela deve misturar para fazer a solução de 15%?

    22. Um cientista precisa de 120 mililitros de uma solução ácida de 20% para um experimento. O laboratório tem disponível uma solução de 25% e 10%. Quantos litros das soluções de 25% e quantos litros de 10% o cientista deve misturar para fazer a solução de 20%?

    Responda

    80 litros da solução de 25% e 40 litros da solução de 10%

    23. Uma solução anticongelante de 40% deve ser misturada com uma solução anticongelante de 70% para obter 240 litros de uma solução de 50%. Quantos litros das soluções de 40% e quantos litros das soluções de 70% serão usados?

    24. Uma solução anticongelante de 90% deve ser misturada com uma solução anticongelante de 75% para obter 360 litros de uma solução de 85%. Quantos litros das soluções de 90% e quantos litros das soluções de 75% serão usados?

    Responda

    240 litros da solução de 90% e 120 litros da solução de 75%

    Resolver aplicativos de interesse

    Nos exercícios a seguir, traduza para um sistema de equações e resolva.

    25. Hattie tinha $3000 para investir e quer ganhar 10,6% de juros ao ano. Ela colocará parte do dinheiro em uma conta que ganha 12% ao ano e o restante em uma conta que ganha 10% ao ano. Quanto dinheiro ela deve colocar em cada conta?

    26. Carol investiu $2560 em duas contas. Uma conta pagou 8% de juros e a outra pagou 6% de juros. Ela ganhou 7,25% de juros sobre o investimento total. Quanto dinheiro ela colocou em cada conta?

    Responda

    $1600 a 8%, 960 a 6%

    27. Sam investiu $48.000, alguns com juros de 6% e o restante com 10%. Quanto ele investiu em cada taxa se recebesse $4000 em juros em um ano?

    28. Arnold investiu $64.000, alguns com 5,5% de juros e o restante com 9%. Quanto ele investiu em cada taxa se recebesse $4.500 em juros em um ano?

    Responda

    $28.000 a 9%, $36.000 a 5,5%

    29. Depois de quatro anos na faculdade, Josie deve $65.800 em empréstimos estudantis. A taxa de juros dos empréstimos federais é de 4,5% e a taxa dos empréstimos bancários privados é de 2%. O total de juros que ela deve por um ano foi\($2878.50\). Qual é o valor de cada empréstimo?

    30. Mark quer investir $10.000 para pagar o casamento de sua filha no próximo ano. Ele investirá parte do dinheiro em um CD de curto prazo que paga 12% de juros e o restante em uma conta poupança do mercado monetário que paga 5% de juros. Quanto ele deve investir em cada taxa se quiser ganhar $1095 em juros em um ano?

    Responda

    CD de $8500, conta poupança de $1500

    31. Um fundo fiduciário no valor de $25.000 é investido em dois portfólios diferentes. Este ano, espera-se que uma carteira ganhe 5,25% de juros e a outra ganhe 4%. Os planos são de que os juros totais sobre o fundo sejam de $1150 em um ano. Quanto dinheiro deve ser investido em cada taxa?

    32. Uma empresa tem dois empréstimos totalizando $85.000. Um empréstimo tem uma taxa de 6% e o outro tem uma taxa de 4,5%. Este ano, a empresa espera pagar $4.650 em juros sobre os dois empréstimos. Quanto custa cada empréstimo?

    Responda

    $55.000 em empréstimo a 6% e $30.000 em empréstimo a 4,5%

    Resolva aplicações de funções de custo e receita

    33. O fabricante de uma bebida energética gasta $1,20 para fazer cada bebida e a vende por $2. O fabricante também tem custos fixos mensais de $8.000.

    ⓐ Encontre a função de custo C quando x bebidas energéticas são fabricadas.

    ⓑ Encontre a função de receita R quando x bebidas forem vendidas.

    ⓒ Mostre o ponto de equilíbrio representando graficamente as funções Receita e Custo na mesma grade.

    ⓓ Encontre o ponto de equilíbrio. Interprete o que significa o ponto de equilíbrio.

    34. O fabricante de uma garrafa de água gasta $5 para construir cada garrafa e as vende por $10. O fabricante também tem custos fixos mensais de $6500. ⓐ Encontre a função de custo C quando x garrafas são fabricadas. ⓑ Encontre a função de receita R quando x garrafas forem vendidas. ⓒ Mostre o ponto de equilíbrio representando graficamente as funções Receita e Custo no mesma grade. ⓓ Encontre o ponto de equilíbrio. Interprete o que significa o ponto de equilíbrio.

    Responda

    ⓐ\(C(x)=5x+6500\)

    ⓑ\(R(x)=10x\)

    ⓒ

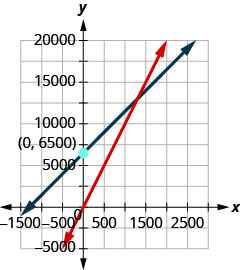
    A figura mostra um gráfico com duas linhas que se cruzam. Um deles passa pela origem. O outro cruza o eixo y no ponto 6560.

    ⓓ 1.500; quando 1.500 garrafas de água são vendidas, o custo e a receita equivalem a $15.000

    exercícios de escrita

    35. Pegue um punhado de dois tipos de moedas e escreva um problema semelhante ao Exemplo relacionando o número total de moedas e seu valor total. Configure um sistema de equações para descrever sua situação e depois resolvê-la.

    36. No exemplo, usamos a eliminação para resolver o sistema de equações
    \(\left\{ \begin{array} {l} s+b=40,000 \\ 0.08s+0.03b=0.071(40,000). \end{array} \right. \)

    Você poderia ter usado a substituição ou a eliminação para resolver esse sistema? Por quê?

    Responda

    As respostas podem variar.

    Verificação automática

    ⓐ Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

    Essa tabela tem 4 colunas, 2 linhas e uma linha de cabeçalho. A linha do cabeçalho rotula cada coluna que eu posso, com confiança, com alguma ajuda e não, eu não entendo. A primeira coluna tem as seguintes declarações: resolver aplicações de mistura, resolver aplicações de interesse. As colunas restantes estão em branco.

    ⓑ O que essa lista de verificação diz sobre o seu domínio desta seção? Quais etapas você tomará para melhorar?