4.4: Resolva aplicações de mistura com sistemas de equações

Last updated
Save as PDF

Page ID: 183169

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Resolver aplicações de mistura
Resolver pedidos de interesse
Resolva aplicações de funções de custo e receita

Antes de começar, faça este teste de prontidão.

Multiplique:$4.025(1,562)$.
Se você perdeu esse problema, revise [link].
Escreva 8,2% como decimal.
Se você perdeu esse problema, revise [link].
A conta do jantar de Earl chegou a $32,50 e ele queria deixar uma gorjeta de 18%. Quanto deve custar a gorjeta?
Se você perdeu esse problema, revise [link].

Resolver aplicações de mistura

A aplicação da mistura envolve a combinação de duas ou mais quantidades. Quando resolvemos aplicativos de mistura com moedas e bilhetes mais cedo, começamos criando uma tabela para que pudéssemos organizar as informações. Para um exemplo de moeda com níquel e moedas de dez centavos, a tabela ficou assim:

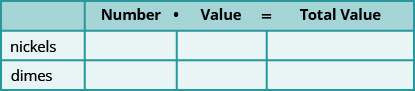
$Essa tabela tem 4 colunas e duas linhas. A primeira coluna rotula cada linha em níquel e moeda de dez centavos. O cabeçalho rotula o número de vezes que o valor da coluna é igual ao valor total.$

Usar uma variável significava que tínhamos que relacionar o número de níquel e o número de moedas de dez centavos. Tivemos que decidir se deixaríamos n ser o número de moedas e depois escrever o número de moedas de dez centavos em termos de n, ou se seríamos d o número de moedas de dez centavos e escreveríamos o número de moedas em termos de d.

Agora que sabemos como resolver sistemas de equações com duas variáveis, vamos deixar n ser o número de níquel e d ser o número de moedas de dez centavos. Escreveremos uma equação com base na coluna de valor total, como fizemos antes, e a outra equação virá da coluna numérica.

No primeiro exemplo, resolveremos um problema de ingressos em que os preços dos ingressos estão em dólares inteiros, então não precisaremos usar decimais ainda.

Exemplo$\PageIndex{1}$

Traduza para um sistema de equações e resolva:

Um centro de ciências vendeu 1.363 ingressos em um fim de semana agitado. Os recibos totalizaram $12.146. Quantos ingressos para adultos de $12 e quantos ingressos para crianças de $7 foram vendidos?

Resposta

Etapa 1. Leia o problema.	Criaremos uma tabela para organizar as informações.
Etapa 2. Identifique o que estamos procurando.	Estamos procurando o número de ingressos para adultos e o número de ingressos infantis vendidos.
Etapa 3. Diga o que estamos procurando.	Deixe$a= \text{the number of adult tickets.}$ $c= \text{the number of child tickets}$
Uma tabela nos ajudará a organizar os dados. Temos dois tipos de ingressos, adultos e crianças.	Escreva em a e c para o número de ingressos.
Escreva o número total de ingressos vendidos na parte inferior da coluna Número.	Ao todo, 1.363 foram vendidos.
Escreva o valor de cada tipo de ingresso na coluna Valor.	O valor de cada ingresso adulto é de $12. O valor de cada ingresso infantil é de $7.
O número vezes o valor fornece o valor total, então o valor total dos ingressos para adultos é$a·12=12a$, e o valor total dos ingressos infantis é$c·7=7c$.	Preencha a coluna Valor total.
Ao todo, o valor total dos ingressos foi de $12.146.	$.$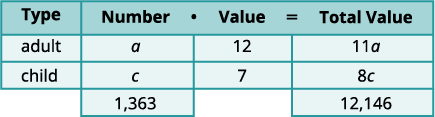
Etapa 4. Traduza em um sistema de equações.
A coluna Número e a coluna Valor total nos fornecem o sistema de equações.	$.$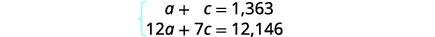
Usaremos o método de eliminação para resolver esse sistema. Multiplique a primeira equação por$−7$.	$.$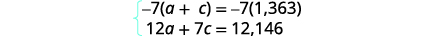
Simplifique e adicione, em seguida, resolva por um.	$.$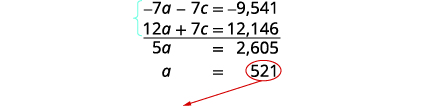
Substitua$a=521$ na primeira equação e resolva por c.	$.$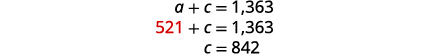
Etapa 6. Verifique a resposta no problema. 521 adultos a $12 por ingresso ganha $6.252 842 criança a $7 por ingresso ganha $58.994 O total de recibos é de $12.146$\checkmark$
Etapa 7. Responda à pergunta.	O centro de ciências vendeu 521 ingressos para adultos e 842 ingressos para crianças.

Exemplo$\PageIndex{2}$

Traduza para um sistema de equações e resolva:

A bilheteria do zoológico vendeu 553 ingressos por dia. Os recibos totalizaram $3.936. Quantos ingressos para adultos de $9 e quantos ingressos infantis de $6 foram vendidos?

Resposta: 206 adultos, 347 crianças

Exemplo$\PageIndex{3}$

Traduza para um sistema de equações e resolva:

A bilheteria de um cinema vendeu 147 ingressos para o show noturno, e as receitas totalizaram $1.302. Quantos ingressos para adultos de $11 e quantos ingressos para crianças de $8 foram vendidos?

Resposta: 42 adultos, 105 crianças

No próximo exemplo, resolveremos um problema com moedas. Agora que sabemos como trabalhar com sistemas de duas variáveis, será fácil nomear as variáveis na coluna “número”.

Exemplo$\PageIndex{4}$

Traduza para um sistema de equações e resolva:

Juan tem um bolso cheio de moedas e moedas de dez centavos. O valor total das moedas é de $8,10. O número de moedas de dez centavos é 9 a menos que o dobro do número de níquel. Quantos centavos e quantos centavos Juan tem?

Resposta

Etapa 1. Leia o problema. Criaremos uma tabela para organizar as informações.
Etapa 2. Identifique o que estamos procurando.	Estamos procurando o número de níquel e o número de moedas de dez centavos.
Etapa 3. Diga o que estamos procurando.	Deixe$n= \text{the number of nickels.}$ $d= \text{the number of dimes}$
Uma tabela nos ajudará a organizar os dados. Temos dois tipos de moedas, níquel e moedas de dez centavos.	Escreva n e d para o número de cada tipo de moeda.
Preencha a coluna Valor com o valor de cada tipo de moeda.	O valor de cada níquel é de $0,05. O valor de cada centavo é de $0,10.
O número vezes o valor fornece o valor total, então, o valor total dos níquel é $n(0.05)=0.05n$ e o valor total das moedas de dez centavos é $d(0.10)=0.10d$. No total, o valor total das moedas é de $8,10.	$.$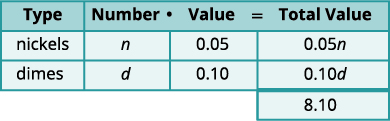
Etapa 4. Traduza em um sistema de equações.
A coluna Valor total fornece uma equação.	$.$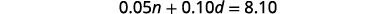
Também sabemos que o número de moedas de dez centavos é 9 a menos que o dobro do número de níquel.
Traduza para obter a segunda equação.	$.$
Agora temos o sistema para resolver.	$.$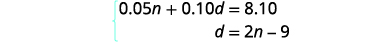
Etapa 5. Resolva o sistema de equações Usaremos o método de substituição.
Substitua$d=2n−9$ na primeira equação.	$.$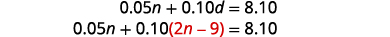
Simplifique e resolva para n.	$.$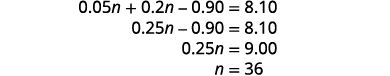
Para encontrar o número de moedas de dez centavos, $n=36$ substitua pela segunda equação.	$.$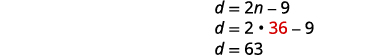
Etapa 6. Verifique a resposta no problema: 63 centavos a$$0.10=$6.30$ 36 níqueis no$$0.05=$1.80$ Total$=$8.10\checkmark$
Etapa 7. Responda à pergunta.	Juan tem 36 centavos e 63 centavos.

Exemplo$\PageIndex{5}$

Traduza para um sistema de equações e resolva:

Matilda tem um punhado de moedas e moedas de dez centavos, com um valor total de $8,55. O número de trimestres é 3 a mais do que o dobro do número de moedas de dez centavos. Quantas moedas de dez centavos e quantas moedas ela tem?

Resposta: 13 moedas de dez centavos e 29 quartos

Exemplo$\PageIndex{6}$

Traduza para um sistema de equações e resolva:

A Priam tem uma coleção de níquel e quartos, com um valor total de $7,30. O número de níquel é seis menos do que três vezes o número de trimestres. Quantos centavos e quantos quartos ele tem?

Resposta: 19 quartos e 51 níquel

Algumas aplicações de misturas envolvem a combinação de alimentos ou bebidas. Exemplos de situações podem incluir a combinação de passas e nozes para fazer uma mistura de trilhas ou usar dois tipos de grãos de café para fazer uma mistura.

Exemplo$\PageIndex{7}$

Traduza para um sistema de equações e resolva:

Carson quer fazer 20 quilos de mix de trilha usando nozes e gotas de chocolate. Seu orçamento exige que o mix de trilhas lhe custe $7,60. por libra. As nozes custam $9,00 por libra e as gotas de chocolate custam $2,00 por libra. Quantos quilos de nozes e quantos quilos de chocolate ele deve usar?

Resposta

Etapa 1. Leia o problema. Criaremos uma tabela para organizar as informações.
Etapa 2. Identifique o que estamos procurando.	Estamos procurando o número de quilos de nozes e o número de quilos de gotas de chocolate.
Etapa 3. Diga o que estamos procurando.	Deixe$n= \text{the number of pound of nuts.}$ $c= \text{the number of pounds of chips}$
Carson misturará nozes e gotas de chocolate para obter uma mistura de trilha. Escreva em n e c para o número de quilos de nozes e gotas de chocolate.	$.$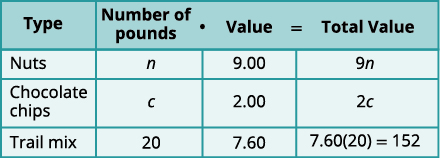
Haverá 20 libras de mistura de trilhas. Coloque o preço por libra de cada item na coluna Valor. Preencha a última coluna usando $\text{Number}•\text{Value}=\text{Total Value}$
Etapa 4. Traduza em um sistema de equações. Obtemos as equações das colunas Número e Valor Total.	$.$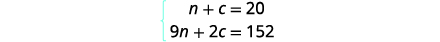
Etapa 5. Resolva o sistema de equações Usaremos a eliminação para resolver o sistema. Multiplique a primeira equação por$−2$ para eliminar c.	$.$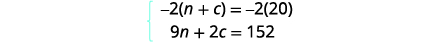
Simplifique e acrescente. Resolva para n.	$.$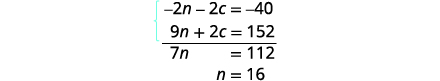
Para encontrar o número de quilos de gotas de chocolate, substitua$n=16$ na primeira equação e resolva por c.	$.$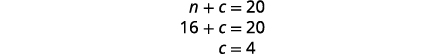
Etapa 6. Verifique a resposta no problema. $\begin{array} {lll} 16+4 &= &20\checkmark \\ 9·16+2·4 &= &152\checkmark \end{array}$
Etapa 7. Responda à pergunta.	Carson deve misturar 16 libras de nozes com 4 libras de gotas de chocolate para criar a mistura de trilhas.

Exemplo$\PageIndex{8}$

Traduza para um sistema de equações e resolva:

Greta quer fazer 5 quilos de uma mistura de nozes usando amendoim e castanha de caju. Seu orçamento exige que a mistura lhe custe $6 por libra. Os amendoins custam $4 por libra e os cajus custam $9 por libra. Quantos quilos de amendoim e quantos quilos de caju ela deve usar?

Resposta: 3 libras de amendoim e 2 libras de caju

Exemplo$\PageIndex{9}$

Traduza para um sistema de equações e resolva:

Sammy tem a maioria dos ingredientes necessários para fazer um grande lote de pimenta. Os únicos itens que lhe faltam são feijão e carne moída. Ele precisa de um total de 20 libras combinadas de feijão e carne moída e tem um orçamento de $3 por libra. O preço do feijão é de $1 por libra e o preço da carne moída é de $5 por libra. Quantos quilos de feijão e quantos quilos de carne moída ele deve comprar?

Resposta: 10 libras de feijão, 10 libras de carne moída

Outra aplicação de problemas de mistura está relacionada a suprimentos de limpeza concentrados, outros produtos químicos e bebidas mistas. A concentração é dada como uma porcentagem. Por exemplo, um limpador doméstico com 20% de concentração significa que 20% da quantidade total é limpador e o restante é água. Para fazer 35 onças de uma concentração de 20%, você mistura 7 onças (20% de 35) do limpador com 28 onças de água.

Para esses tipos de problemas de mistura, usaremos “porcentagem” em vez de “valor” para uma das colunas em nossa tabela.

Exemplo$\PageIndex{10}$

Traduza para um sistema de equações e resolva:

Sasheena é assistente de laboratório em sua faculdade comunitária. Ela precisa fazer 200 mililitros de uma solução de 40% de ácido sulfúrico para um experimento de laboratório. O laboratório tem apenas 25% e 50% de soluções no depósito. Quanto ela deve misturar das soluções de 25% e 50% para fazer a solução de 40%?

Resposta

Etapa 1. Leia o problema. Uma figura pode nos ajudar a visualizar a situação e, em seguida, criaremos uma tabela para organizar as informações.	Sasheena deve misturar parte da$25%$ solução e parte da$50%$ solução para obter$200\space ml$ a$40%$ solução.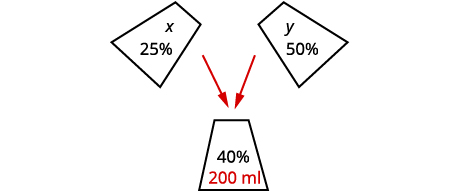
	$.$
Etapa 2. Identifique o que estamos procurando.	Estamos procurando a quantidade de cada solução que ela precisa.
Etapa 3. Diga o que estamos procurando.	Deixe$x= \text{number of }ml\text{ of }25% \text{ solution.}$ $y= \text{number of }ml\text{ of }50%\text{ solution$
Uma tabela nos ajudará a organizar os dados. Ela misturará x$ml$ de$25%$ com y$ml$ de$50%$ para obter$200 \space ml$ a$40%$ solução. Escrevemos as porcentagens como decimais no gráfico. Multiplicamos o número de unidades vezes a concentração para obter a quantidade total de ácido sulfúrico em cada solução.	$.$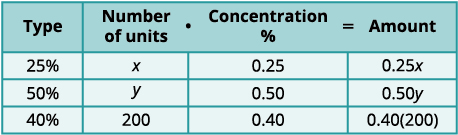
Etapa 4. Traduza em um sistema de equações. Obtemos as equações da coluna Número e da coluna Quantidade. Agora temos o sistema.	$.$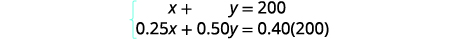
Etapa 5. Resolva o sistema de equações Resolveremos o sistema por eliminação. Multiplique a primeira equação por$−0.5$ para eliminar y.	$.$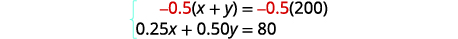
Simplifique e adicione para resolver x.	$.$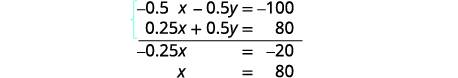
Para resolver y, substitua$x=80$ na primeira equação.	$.$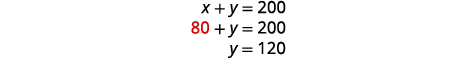
Etapa 6. Verifique a resposta no problema. $\begin{array} {lll} 80+120 &= &200\checkmark \\ 0.25(80)+0.50(120) &= &200\checkmark \\ {} &{} &\text{Yes!} \end{array} $
Etapa 7. Responda à pergunta.	Sasheena deve misturar$80 \space ml$ a$25%$ solução com $120 \space ml$ a$50%$ solução para obter$200\space ml$ a $40%$ solução.

Exemplo$\PageIndex{11}$

Traduza para um sistema de equações e resolva:

LeBron precisa de 150 mililitros de uma solução de 30% de ácido sulfúrico para um experimento de laboratório, mas só tem acesso a uma solução de 25% e 50%. Quanto da solução de 25% e quanto da solução de 50% ele deve misturar para fazer a solução de 30%?

Resposta: 120 ml de solução a 25% e 30 ml de solução a 50%

Exemplo$\PageIndex{12}$

Traduza para um sistema de equações e resolva:

A Anatole precisa produzir 250 mililitros de uma solução de 25% de ácido clorídrico para um experimento de laboratório. O laboratório tem apenas uma solução de 10% e uma solução de 40% no depósito. Quanto das soluções de 10% e de 40% ele deve misturar para fazer a solução de 25%?

Resposta: 125 ml de solução a 10% e 125 ml de solução a 40%

Resolver aplicativos de interesse

A fórmula para modelar pedidos de juros simples é$I=Prt$. Os juros, I, são o produto do principal, P, a taxa, r, e o tempo, t. Em nosso trabalho aqui, calcularemos os juros ganhos em um ano, então serão 1.

Modificamos os títulos das colunas na tabela de mistura para mostrar a fórmula de interesse, como você verá no próximo exemplo.

Traduza para um sistema de equações e resolva:

Adnan tem $40.000 para investir e espera ganhar$7.1%$ juros por ano. Ele colocará parte do dinheiro em um fundo de ações que ganha 8% ao ano e o restante em títulos que rendem 3% ao ano. Quanto dinheiro ele deve investir em cada fundo?

Resposta

Etapa 1. Leia o problema.	Um gráfico nos ajudará a organizar as informações.
Etapa 2. Identifique o que estamos procurando.	Estamos procurando o valor para investir em cada fundo.
Etapa 3. Diga o que estamos procurando.	Deixe$s= \text{the amount invested in stocks.}$ $b= \text{the amount invested in stocks}$
Escreva a taxa de juros como decimal para cada fundo. Multiplique: Principal · Taxa · Tempo	$.$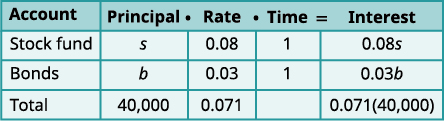
Etapa 4. Traduza em um sistema de equações. Obtemos nosso sistema de equações da coluna Principal e da coluna Interesse.	$.$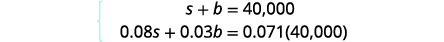
Etapa 5. Resolva o sistema de equações por eliminação. Multiplique a equação superior por$−0.03$.	$.$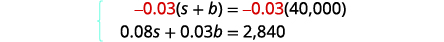
Simplifique e adicione para resolver para s.	$.$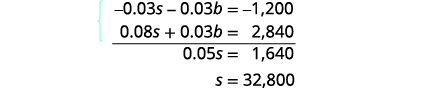
Para encontrar b, substitua s = 32.800 na primeira equação.	$.$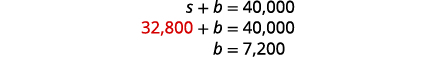
Etapa 6. Verifique a resposta no problema.	Deixamos o cheque para você.
Etapa 7. Responda à pergunta.	Adnan deve investir $32.800 em ações e $7.200 em títulos.

Você notou que a coluna Principal representa o valor total de dinheiro investido, enquanto a coluna Juros representa apenas os juros ganhos? Da mesma forma, a primeira equação em nosso sistema,$s+b=40,000$, represents the total amount of money invested and the second equation, $0.08s+0.03b=0.071(40,000)$, represents the interest earned.

Exemplo$\PageIndex{14}$

Traduza para um sistema de equações e resolva:

Leon tinha $50.000 para investir e espera ganhar$6.2%$ juros por ano. Ele colocará parte do dinheiro em um fundo de ações que ganha 7% ao ano e o restante em uma conta poupança que ganha 2% ao ano. Quanto dinheiro ele deve investir em cada fundo?

Resposta: $42.000 no fundo de ações e $8000 na conta poupança

Exemplo$\PageIndex{15}$

Traduza para um sistema de equações e resolva:

Julius investiu $7000 em dois investimentos em ações. Uma ação pagou 11% de juros e a outra ação pagou 13% de juros. Ele ganhou$12.5%$ juros sobre o investimento total. Quanto dinheiro ele investiu em cada ação?

Resposta: $1750 a 11% e $5250 a 13%

O próximo exemplo exige que encontremos o principal, considerando a quantidade de juros auferidos.

Exemplo$\PageIndex{16}$

Traduza para um sistema de equações e resolva:

Rosie deve $21.540 em seus dois empréstimos estudantis. A taxa de juros do empréstimo bancário dela é$10.5%$ e a taxa de juros do empréstimo federal é$5.9%$. O valor total dos juros que ela pagou no ano passado foi$$1,669.68$. Qual era o principal de cada empréstimo?

Resposta

Etapa 1. Leia o problema.	Um gráfico nos ajudará a organizar as informações.
Etapa 2. Identifique o que estamos procurando.	Estamos procurando o principal de cada empréstimo.
Etapa 3. Diga o que estamos procurando.	Deixe$b= \text{the principal for the bank loan.}$ $f= \text{the principal on the federal loan}$
O total de empréstimos é de $21.540.
Registre as taxas de juros como decimais no gráfico. Multiplique usando a fórmula I = Prt para obter os juros.	$.$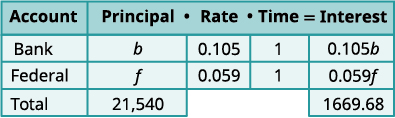
Etapa 4. Traduza em um sistema de equações. O sistema de equações vem da coluna Principal e da coluna Interesse.	$.$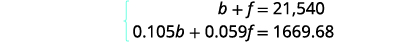
Etapa 5. Resolva o sistema de equações Usaremos a substituição para resolver. Resolva a primeira equação para b.	$.$
	$.$
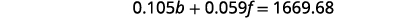
Substitua b = − f + 21,540 na segunda equação.	$.$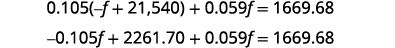
Simplifique e resolva para f.	$.$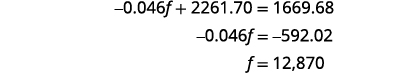
Para encontrar b, substitua f = 12.870 na primeira equação.	$.$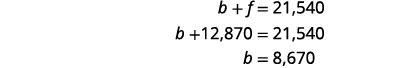
Etapa 6. Verifique a resposta no problema.	Deixamos o cheque para você.
Etapa 7. Responda à pergunta.	O principal do empréstimo federal foi de $12.870 e o principal do empréstimo bancário foi de $8.670.

Exemplo$\PageIndex{17}$

Traduza para um sistema de equações e resolva:

Laura deve $18.000 em seus empréstimos estudantis. A taxa de juros do empréstimo bancário é de 2,5% e a taxa de juros do empréstimo federal é de 6,9%. O valor total de juros que ela pagou no ano passado foi de $1.066. Qual era o principal de cada empréstimo?

Resposta: Banco $4.000; Federal $14.000

Exemplo$\PageIndex{18}$

Traduza para um sistema de equações e resolva:

A Jill's Sandwich Shoppe deve $65.200 em dois empréstimos comerciais, um com juros de 4,5% e outro com juros de 7,2%. O valor total dos juros devidos no ano passado foi de $3.582. Qual era o principal de cada empréstimo?

Resposta: $41.200 a 4,5%, $24.000 a 7,2%

Resolva aplicações de funções de custo e receita

Suponha que uma empresa produza e venda x unidades de um produto. O custo para a empresa é o custo total de produção de x unidades. Esse é o custo de fabricação de cada unidade vezes x, o número de unidades fabricadas, mais os custos fixos.

A receita é o dinheiro que a empresa gera como resultado da venda de x unidades. Esse é o preço de venda de cada unidade vezes o número de unidades vendidas.

Quando os custos são iguais à receita, dizemos que a empresa atingiu o ponto de equilíbrio.

FUNÇÕES DE CUSTO E RECEITA

A função de custo é o custo de fabricação de cada unidade vezes x, o número de unidades fabricadas, mais os custos fixos.

\[C(x)=(\text{cost per unit})·x+\text{fixed costs}\nonumber \]

A função de receita é o preço de venda de cada unidade vezes x, o número de unidades vendidas.

\[R(x)=(\text{selling price per unit})·x\nonumber \]

O ponto de equilíbrio é quando a receita é igual aos custos.

\[C(x)=R(x)\nonumber\]

Exemplo$\PageIndex{19}$

O fabricante de um banco de musculação gasta $105 para construir cada banco e os vende por $245. O fabricante também tem custos fixos mensais de $7.000.

ⓐ Encontre a função de custo C quando x bancos são fabricados.

ⓑ Encontre a função de receita R quando x bancos forem vendidos.

ⓓ Encontre o ponto de equilíbrio. Interprete o que significa o ponto de equilíbrio.

Resposta

ⓐ O fabricante tem $7.000 em custos fixos, independentemente da quantidade de bancos de musculação que produza. Além dos custos fixos, o fabricante também gasta $105 para produzir cada bancada. Suponha que x bancos sejam vendidos.

$\begin{array} {ll} {\text{Write the general Cost function formula.}} &{C(x)=(\text{cost per unit})·x+\text{fixed costs}} \\ {\text{Substitute in the cost values.}} &{C(x)=105x+7000} \\ \end{array}$

ⓑ O fabricante vende cada banco de musculação por $245. Obtemos a receita total multiplicando a receita por unidade pelo número de unidades vendidas.

$\begin{array} {ll} {\text{Write the general Revenue function.}} &{C(x)=(\text{selling price per unit})·x} \\ {\text{Substitute in the revenue per unit.}} &{R(x)=245x} \\ \end{array}$

\[\left\{ \begin{array} {l} C(x)=105x+7000 \\ R(x)=245x \end{array} \right. \quad \text{or} \quad \left\{ \begin{array} {l} y=105x+7000 \\ y=245x \end{array} \right. \nonumber \]

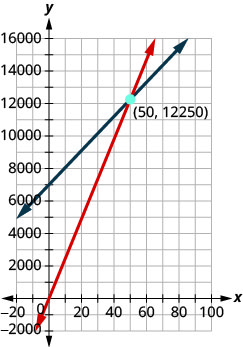
$A figura mostra um gráfico com duas linhas que se cruzam. Um deles passa pela origem.$

ⓓ Para encontrar o valor real, lembramos que o ponto de equilíbrio ocorre quando os custos são iguais à receita.

$\begin{array} {ll} {\text{Write the break-even formula.}} &{\begin{array} {l} {C(x)=R(x)} \\ {105x+7000=245x} \end{array}} \\ {\text{Solve.}} &{\begin{array} {l} {7000=140x} \\ {50=x} \end{array}} \\ \end{array}$

Quando 50 bancos são vendidos, os custos são iguais à receita.

$C de x é 105x mais 7000. C de 50 é 105 vezes 50 mais 7000, o que é igual a 12250. R de x é 245x. R de 50 é 245 vezes 50, o que é 12250.$

Quando 50 bancos são vendidos, a receita e os custos são de $12.250. Observe que isso corresponde ao par pedido$(50,12250)$.

Exemplo$\PageIndex{20}$

O fabricante de um banco de musculação gasta $15 para construir cada banco e os vende por $32. O fabricante também tem custos fixos mensais de $25.500.

ⓐ Encontre a função de custo C quando x bancos são fabricados.

ⓑ Encontre a função de receita R quando x bancos forem vendidos.

ⓓ Encontre o ponto de equilíbrio. Interprete o que significa o ponto de equilíbrio.

Resposta

ⓐ$C(x)=15x+25,500$

ⓑ$R(x)=32x$

ⓒ

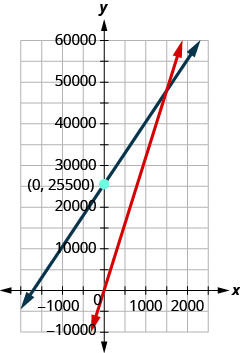
$A figura mostra um gráfico com duas linhas que se cruzam. Um deles passa pela origem. O outro cruza o eixo y no ponto 25.687.$

ⓓ 1.5001.500; quando 1.500 bancos forem vendidos, o custo e a receita serão de 48.000

Exemplo$\PageIndex{21}$

O fabricante de um banco de musculação gasta $120 para construir cada banco e os vende por $170. O fabricante também tem custos fixos mensais de $150.000.

ⓐ Encontre a função de custo C quando x bancos são fabricados.

ⓑ Encontre a função de receita R quando x bancos forem vendidos.

ⓓ Encontre o ponto de equilíbrio. Interprete o que significa o ponto de equilíbrio.

Resposta

ⓐ$C(x)=120x+150,000$

ⓑ$R(x)=170x$

ⓒ

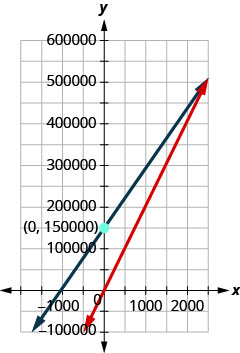
$A figura mostra um gráfico com duas linhas que se cruzam. Um deles passa pela origem.$

ⓓ$3,000$; quando 3.000 bancos são vendidos, a receita e os custos são de $510.000

Acesse este recurso on-line para obter instruções e práticas adicionais com interesses e misturas.

Interesse e misturas

Conceitos chave

Função de custo: A função de custo é o custo de fabricação de cada unidade vezes x, o número de unidades fabricadas, mais os custos fixos.
$C(x)=(\text{cost per unit})·x+\text{fixed costs}$
Receita: A função de receita é o preço de venda de cada unidade vezes x, o número de unidades vendidas.
$R(x)=(\text{selling price per unit})·x$
Ponto de equilíbrio: O ponto de equilíbrio é quando a receita é igual aos custos.
$C(x)=R(x)$

Glossário

função de custo: A função de custo é o custo de fabricação de cada unidade vezes xx, o número de unidades fabricadas, mais os custos fixos; C (x) = (custo por unidade) x + custos fixos.

receita: A receita é o preço de venda de cada unidade vezes x, o número de unidades vendidas; R (x) = (preço de venda por unidade) x.

ponto de equilíbrio: O ponto em que a receita é igual aos custos é o ponto de equilíbrio; C (x) =R (x).

Exemplo\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\)

Exemplo\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\)

Exemplo\(\PageIndex{6}\)

Exemplo\(\PageIndex{7}\)

Exemplo\(\PageIndex{8}\)

Exemplo\(\PageIndex{9}\)

Exemplo\(\PageIndex{10}\)

Exemplo\(\PageIndex{11}\)

Exemplo\(\PageIndex{12}\)

Exemplo\(\PageIndex{14}\)

Exemplo\(\PageIndex{15}\)

Exemplo\(\PageIndex{16}\)

Exemplo\(\PageIndex{17}\)

Exemplo\(\PageIndex{18}\)

FUNÇÕES DE CUSTO E RECEITA

Exemplo\(\PageIndex{19}\)

Exemplo\(\PageIndex{20}\)

Exemplo\(\PageIndex{21}\)

Etapa 1. Leia o problema. Uma figura pode nos ajudar a visualizar a situação e, em seguida, criaremos uma tabela para organizar as informações.	Sasheena deve misturar parte da\(25%\) solução e parte da\(50%\) solução para obter\(200\space ml\) a\(40%\) solução.
	$.$
Etapa 2. Identifique o que estamos procurando.	Estamos procurando a quantidade de cada solução que ela precisa.
Etapa 3. Diga o que estamos procurando.	Deixe\(x= \text{number of }ml\text{ of }25% \text{ solution.}\) \(y= \text{number of }ml\text{ of }50%\text{ solution\)
Uma tabela nos ajudará a organizar os dados. Ela misturará x\(ml\) de\(25%\) com y\(ml\) de\(50%\) para obter\(200 \space ml\) a\(40%\) solução. Escrevemos as porcentagens como decimais no gráfico. Multiplicamos o número de unidades vezes a concentração para obter a quantidade total de ácido sulfúrico em cada solução.	$.$
Etapa 4. Traduza em um sistema de equações. Obtemos as equações da coluna Número e da coluna Quantidade. Agora temos o sistema.	$.$
Etapa 5. Resolva o sistema de equações Resolveremos o sistema por eliminação. Multiplique a primeira equação por\(−0.5\) para eliminar y.	$.$
Simplifique e adicione para resolver x.	$.$
Para resolver y, substitua\(x=80\) na primeira equação.	$.$
Etapa 6. Verifique a resposta no problema. \(\begin{array} {lll} 80+120 &= &200\checkmark \\ 0.25(80)+0.50(120) &= &200\checkmark \\ {} &{} &\text{Yes!} \end{array} \)
Etapa 7. Responda à pergunta.	Sasheena deve misturar\(80 \space ml\) a\(25%\) solução com \(120 \space ml\) a\(50%\) solução para obter\(200\space ml\) a \(40%\) solução.