Loading [MathJax]/extensions/TeX/boldsymbol.js
Skip to main content
Library homepage
 
Global

3.7: Gráficos de funções

  1. CCBY
  2. Last updated
    Nov 1, 2022
  3. Page ID
    183128
  4. Save as PDF

Objetivos de

Ao final desta seção, você poderá:

  • Use o teste de linha vertical
  • Identifique gráficos de funções básicas
  • Leia informações de um gráfico de uma função

Antes de começar, faça este teste de prontidão.

  1. Avalie: ⓐ2^3 ⓑ3^2.
    Se você perdeu esse problema, revise [link].
  2. Avalie: ⓐ|7| ⓑ|−3|.
    Se você perdeu esse problema, revise [link].
  3. Avalie: ⓐ\sqrt{4} ⓑ\sqrt{16}.
    Se você perdeu esse problema, revise [link].

Use o teste de linha vertical

Na última seção, aprendemos como determinar se uma relação é uma função. As relações que analisamos foram expressas como um conjunto de pares ordenados, um mapeamento ou uma equação. Agora veremos como saber se um gráfico é o de uma função.

Um par ordenado(x,y) é uma solução de uma equação linear, se a equação for uma afirmação verdadeira quando os valores x e y do par ordenado forem substituídos na equação.

O gráfico de uma equação linear é uma linha reta onde cada ponto na linha é uma solução da equação e cada solução dessa equação é um ponto nessa linha.

Na Figura, podemos ver que, no gráfico da equaçãoy=2x−3, para cada valor x há apenas um valor y, conforme mostrado na tabela anexa.

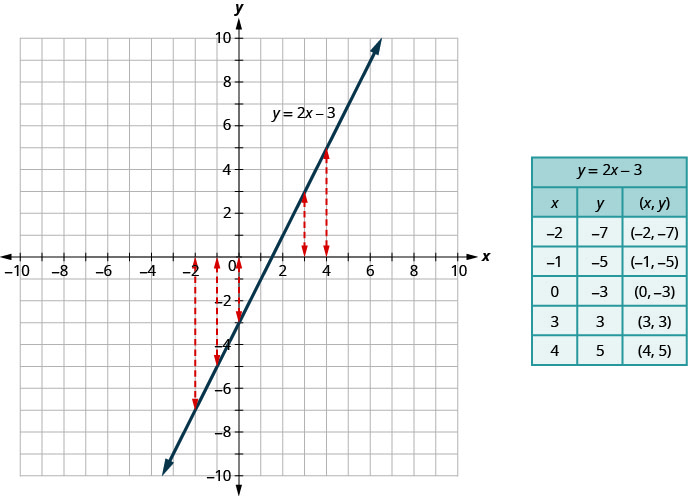
avião. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, menos 3), (1, menos 1) e (2, 1). A linha é rotulada como y igual a 2 x menos 3. Há várias setas verticais que relacionam valores no eixo x com pontos na linha. A primeira seta relaciona x igual a menos 2 no eixo x ao ponto (menos 2, menos 7) na linha. A segunda seta relaciona x igual a menos 1 no eixo x ao ponto (menos 1, menos 5) na linha. A próxima seta relaciona x igual a 0 no eixo x ao ponto (0, menos 3) na linha. A próxima seta relaciona x igual a 3 no eixo x ao ponto (3, 3) na linha. A última seta relaciona x igual a 4 no eixo x ao ponto (4, 5) na linha. A tabela tem 7 linhas e 3 colunas. A primeira linha é uma linha de título com o rótulo y igual a 2 x menos 3. A segunda linha é uma linha de cabeçalho com os cabeçalhos x, y e (x, y). A terceira linha tem as coordenadas menos 2, menos 7 e (menos 2, menos 7). A quarta linha tem as coordenadas menos 1, menos 5 e (menos 1, menos 5). A quinta linha tem as coordenadas 0, menos 3 e (0, menos 3). A sexta linha tem as coordenadas 3, 3 e (3, 3). A sétima linha tem as coordenadas 4, 5 e (4, 5).
Figura\PageIndex{1}

Uma relação é uma função se cada elemento do domínio tiver exatamente um valor no intervalo. Portanto, a relação definida pela equaçãoy=2x−3 é uma função.

Se olharmos para o gráfico, cada linha tracejada vertical só cruza a linha em um ponto. Isso faz sentido, pois em uma função, para cada valor x, há apenas um valor y.

Se a linha vertical atingir o gráfico duas vezes, o valor x seria mapeado para dois valores y e, portanto, o gráfico não representaria uma função.

Isso nos leva ao teste da linha vertical. Um conjunto de pontos em um sistema de coordenadas retangulares é o gráfico de uma função se cada linha vertical cruzar o gráfico em no máximo um ponto. Se alguma linha vertical cruzar o gráfico em mais de um ponto, o gráfico não representa uma função.

TESTE DE LINHA VERTICAL

Um conjunto de pontos em um sistema de coordenadas retangulares é o gráfico de uma função se cada linha vertical cruzar o gráfico em no máximo um ponto.

Se alguma linha vertical cruzar o gráfico em mais de um ponto, o gráfico não representa uma função.

Exemplo\PageIndex{1}

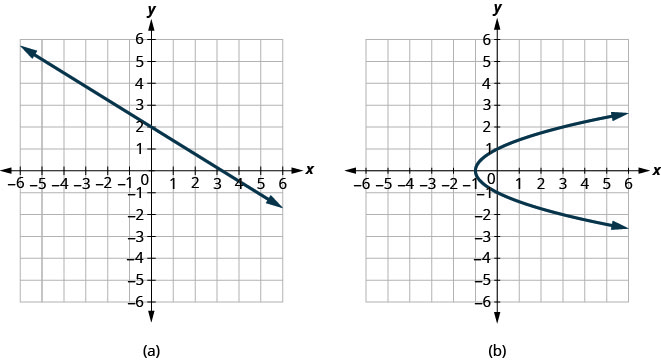
Determine se cada gráfico é o gráfico de uma função.

A figura tem dois gráficos. No gráfico a, há uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, 2), (3, 0) e (6, menos 2). No gráfico b, há uma parábola que se abre à direita representada graficamente no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. A parábola passa pelos pontos (menos 1, 0), (0, 1), (0, menos 1), (3, 2) e (3, menos 2).

Responda

ⓐ Como qualquer linha vertical cruza o gráfico em no máximo um ponto, o gráfico é o gráfico de uma função.

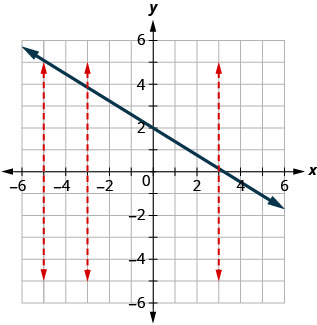
A figura tem uma linha reta representada graficamente no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, 2), (3, 0) e (6, menos 2). Três linhas retas verticais tracejadas são desenhadas em x igual a menos 5, x é igual a menos 3 e x é igual a 3. Cada linha cruza a linha inclinada em exatamente um ponto.

ⓑ Uma das linhas verticais mostradas no gráfico a cruza em dois pontos. Esse gráfico não representa uma função.

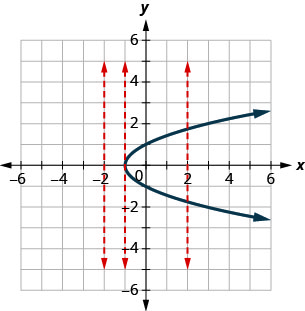
A figura tem uma abertura de parábola à direita representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 6 a 6. A parábola passa pelos pontos (menos 1, 0), (0, 1), (0, menos 1), (3, 2) e (3, menos 2). Três linhas retas verticais tracejadas são desenhadas em x igual a menos 2, x é igual a menos 1 e x é igual a 2. A linha vertical x — menos 2 não cruza a parábola. A linha vertical x é igual a menos 1 cruza a parábola em exatamente um ponto. A linha vertical x é igual a 3 cruza a parábola em dois pontos separados.

Exemplo\PageIndex{2}

Determine se cada gráfico é o gráfico de uma função.

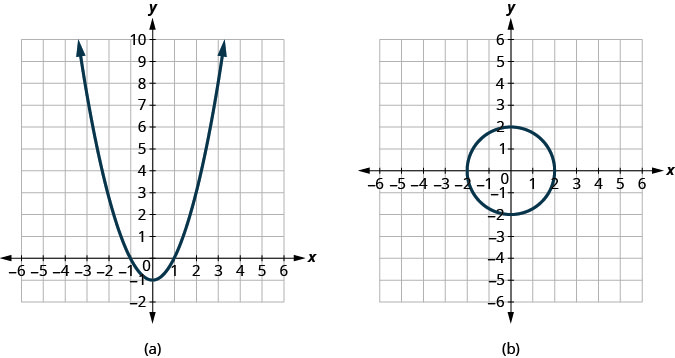
A figura tem dois gráficos. No gráfico a, há uma parábola que se abre representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. A parábola passa pelos pontos (0, menos 1), (menos 1, 0), (1, 0), (menos 2, 3) e (2, 3). No gráfico b, há um círculo representado graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. O círculo passa pelos pontos (menos 2, 0), (2, 0), (0, menos 2) e (0, 2).

Responda

ⓐ sim ⓑ não

Exemplo\PageIndex{3}

Determine se cada gráfico é o gráfico de uma função.

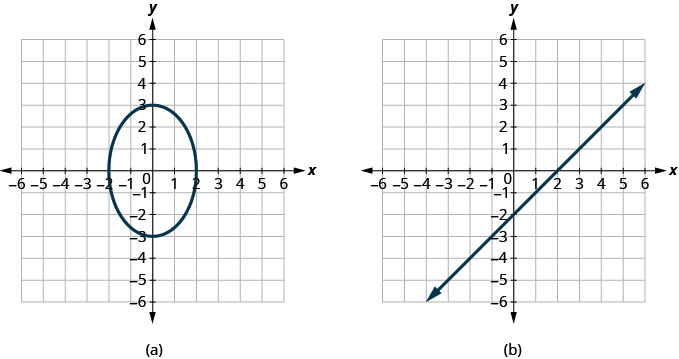
A figura tem dois gráficos. No gráfico a, há uma elipse representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A elipse passa pelos pontos (0, menos 3), (menos 2, 0), (2, 0) e (0, 3). No gráfico b, há uma linha reta representada graficamente no plano de coordenadas x y. O eixo x vai de menos 12 a 12. O eixo y vai de menos 12 a 12. A linha passa pelos pontos (0, menos 2), (2, 0) e (4, 2).

Responda

ⓐ não ⓑ sim

Identifique gráficos de funções básicas

Usamos a equaçãoy=2x−3 e seu gráfico à medida que desenvolvemos o teste da linha vertical. Dissemos que a relação definida pela equaçãoy=2x−3 é uma função.

Podemos escrever isso como na notação de função comof(x)=2x−3. Ainda significa a mesma coisa. O gráfico da função é o gráfico de todos os pares ordenados(x,y) ondey=f(x). Assim, podemos escrever os pares ordenados como(x,f(x)). Parece diferente, mas o gráfico será o mesmo.

Compare o gráfico mostradoy=2x−3 anteriormente na Figura com o gráficof(x)=2x−3 mostrado na Figura. Nada mudou, exceto a notação.

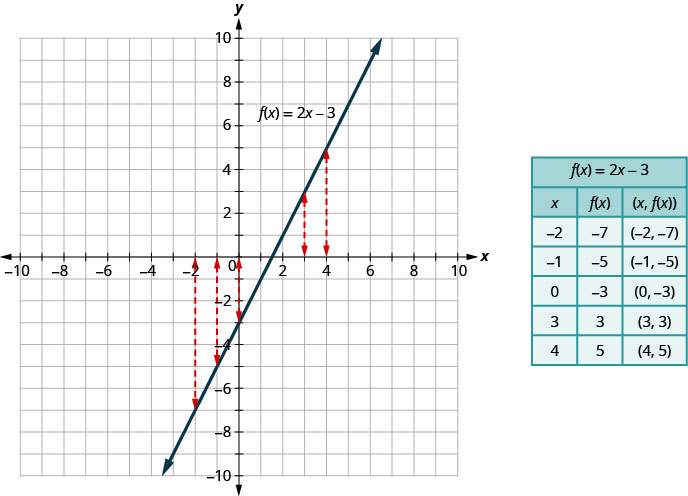
Essa figura tem um gráfico ao lado de uma tabela. O gráfico tem uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, menos 3), (1, menos 1) e (2, 1). A linha é rotulada como f de x igual a 2 x menos 3. Há várias setas verticais que relacionam valores no eixo x com pontos na linha. A primeira seta relaciona x igual a menos 2 no eixo x ao ponto (menos 2, menos 7) na linha. A segunda seta relaciona x igual a menos 1 no eixo x ao ponto (menos 1, menos 5) na linha. A próxima seta relaciona x igual a 0 no eixo x ao ponto (0, menos 3) na linha. A próxima seta relaciona x igual a 3 no eixo x ao ponto (3, 3) na linha. A última seta relaciona x igual a 4 no eixo x ao ponto (4, 5) na linha. A tabela tem 7 linhas e 3 colunas. A primeira linha é uma linha de título com o rótulo f de x igual a 2 x menos 3. A segunda linha é uma linha de cabeçalho com os cabeçalhos x, f de x e (x, f de x). A terceira linha tem as coordenadas menos 2, menos 7 e (menos 2, menos 7). A quarta linha tem as coordenadas menos 1, menos 5 e (menos 1, menos 5). A quinta linha tem as coordenadas 0, menos 3 e (0, menos 3). A sexta linha tem as coordenadas 3, 3 e (3, 3). A sétima linha tem as coordenadas 4, 5 e (4, 5).
Figura\PageIndex{2}
GRÁFICO DE UMA FUNÇÃO

O gráfico de uma função é o gráfico de todos os seus pares ordenados, (x, y) (x, y) ou usando a notação da função, (x, f (x)) (x, f (x)) onde y=f (x) .y=f (x).

\begin{array} {ll} {f} &{\text{name of function}} \\ {x} &{\text{x-coordinate of the ordered pair}} \\ {f(x)} &{\text{y-coordinate of the ordered pair}} \\ \nonumber \end{array}

À medida que avançamos em nosso estudo, é útil estar familiarizado com os gráficos de várias funções básicas e ser capaz de identificá-las.

Por meio de nossos trabalhos anteriores, estamos familiarizados com os gráficos de equações lineares. O processo que usamos para decidir sey=2x−3 é uma função se aplicaria a todas as equações lineares. Todas as equações lineares não verticais são funções. As linhas verticais não são funções, pois o valor x tem infinitos valores y.

Escrevemos equações lineares em várias formas, mas será muito útil para nós aqui usar a forma de interceptação de inclinação da equação linear. A forma de interceptação de inclinação de uma equação linear éy=mx+b. Na notação de função, essa função linear se tornaf(x)=mx+b onde m é a inclinação da linha e b é o intercepto y.

O domínio é o conjunto de todos os números reais e o intervalo também é o conjunto de todos os números reais.

FUNÇÃO LINEAR

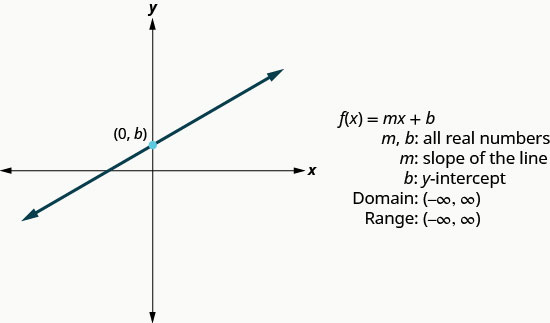
Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. A linha passa pelo ponto (0, b). Ao lado do gráfico estão os seguintes: “f de x é igual a x mais b”, “m, b: todos os números reais”, “m: inclinação da linha”, “b: intercepto y”, “Domínio: (infinito negativo, infinito)” e “Alcance: (infinito negativo, infinito)”.

Usaremos as técnicas gráficas que usamos anteriormente para representar graficamente as funções básicas.

Exemplo\PageIndex{4}

Gráfico:f(x)=−2x−4.

Responda
  f(x)=−2x−4
Nós reconhecemos isso como uma função linear.  
Encontre a inclinação e a interceptação y. m=−2
b=−4
Gráfico usando o intercepto de inclinação. .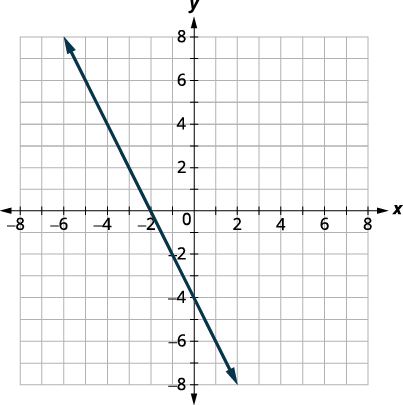
Exemplo\PageIndex{5}

Gráfico:f(x)=−3x−1

Responda

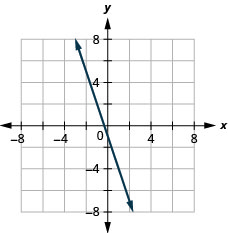
A figura tem o gráfico de uma função linear no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. A linha passa pelos pontos (1, menos 4), (0, menos 1) e (menos 1, 2).

Exemplo\PageIndex{6}

Gráfico:f(x)=−4x−5

Responda

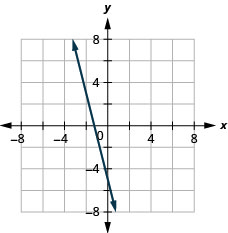
A figura tem o gráfico de uma função linear no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. A linha passa pelos pontos (menos 2, 3), (0, menos 5) e (menos 1, menos 1).

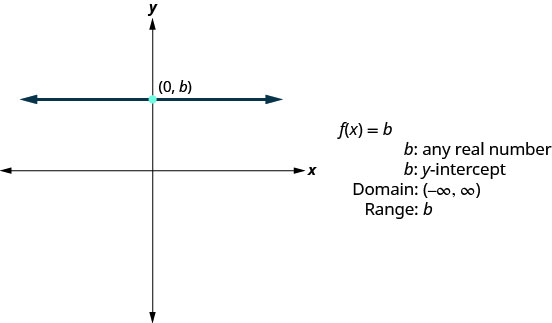
A próxima função cujo gráfico examinaremos é chamada de função constante e sua equação é da formaf(x)=b, onde b é qualquer número real. Se substituirmos of(x) por y, obteremosy=b. Nós reconhecemos isso como a linha horizontal cujo intercepto y é b. O gráfico da funçãof(x)=b também é a linha horizontal cujo intercepto y é b.

Observe que para qualquer número real que colocarmos na função, o valor da função será b. Isso nos diz que o intervalo tem apenas um valor, b.

FUNÇÃO CONSTANTE

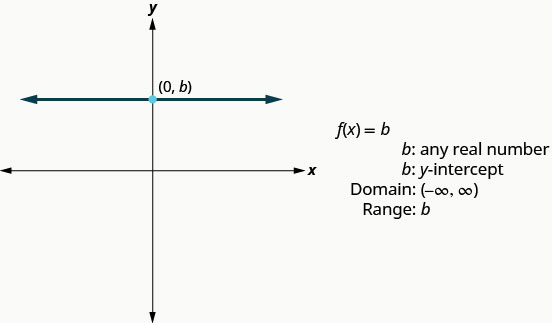
Esta figura tem um gráfico de uma linha reta horizontal no plano de coordenadas x y. A linha passa pelo ponto (0, b). Ao lado do gráfico estão os seguintes: “f de x é igual a sb”, “b: qualquer número real”, “b: intercepto y”, “Domínio: (infinito negativo, infinito)” e “Alcance: b”.

Exemplo\PageIndex{7}

Gráfico:f(x)=4.

Responda
  f(x)=4
Nós reconhecemos isso como uma função constante.  
O gráfico será uma linha horizontal de passagem(0,4). .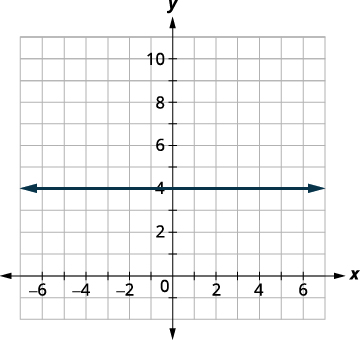
Exemplo\PageIndex{8}

Gráfico:f(x)=−2.

Responda

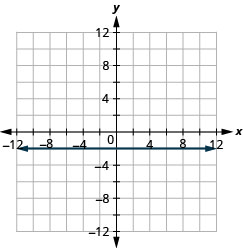
A figura tem o gráfico de uma função constante no plano da coordenada x y. O eixo x vai de menos 12 a 12. O eixo y vai de menos 12 a 12. A linha passa pelos pontos (0, menos 2), (1, menos 2) e (2, menos 2).

Exemplo\PageIndex{9}

Gráfico:f(x)=3.

Responda

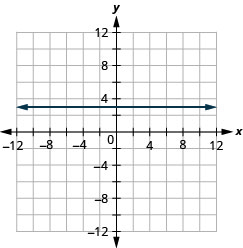
A figura tem o gráfico de uma função constante no plano da coordenada x y. O eixo x vai de menos 12 a 12. O eixo y vai de menos 12 a 12. A linha passa pelos pontos (0, 3), (1, 3) e (2, 3).

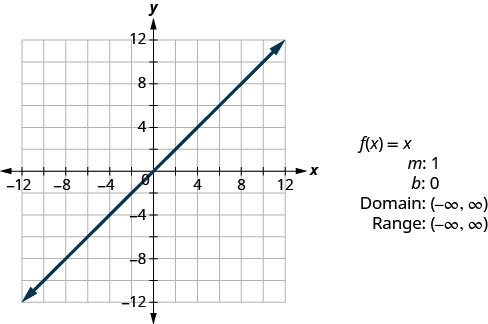
A função de identidadef(x)=x é um caso especial da função linear. Se escrevermos em forma de função linearf(x)=1x+0, vemos que a inclinação é 1 e o intercepto y é 0.

FUNÇÃO DE IDENTIDADE

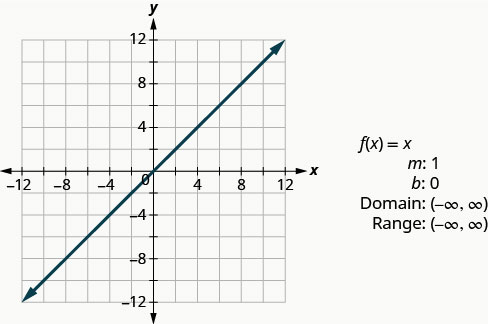
Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. A linha passa pelos pontos (0, 0), (1, 1) e (2, 2). Ao lado do gráfico estão os seguintes: “f de x é igual a x”, “m: 1”, “b: 0”, “Domínio: (infinito negativo, infinito)” e “Alcance: (infinito negativo, infinito)”.

A próxima função que examinaremos não é uma função linear. Portanto, o gráfico não será uma linha. O único método que temos para representar graficamente essa função é a plotagem de pontos. Como essa é uma função desconhecida, nos certificamos de escolher vários valores positivos e negativos, bem como 0 para nossos valores x.

Gráfico:f(x)=x^2.

Responda

Nós escolhemos valores x. Nós os substituímos e, em seguida, criamos um gráfico conforme mostrado.

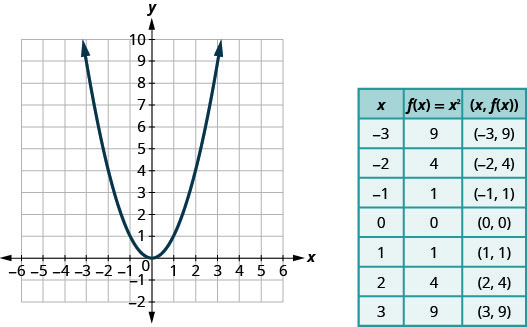
Essa figura tem um gráfico ao lado de uma tabela. No gráfico, há uma parábola que se abre representada graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 2 a 6. A parábola passa pelos pontos (menos 3, 9), (menos 2, 4), (menos 1, 1), (0, 0), (1, 1), (2, 4) e (3, 9). A tabela tem 8 linhas e 3 colunas. A primeira linha é uma linha de cabeçalho com os cabeçalhos x, f de x iguais a x ao quadrado e (x, f de x). A segunda linha tem as coordenadas menos 3, 9 e (menos 3, 9). A terceira linha tem as coordenadas menos 2, 4 e (menos 2, 4). A quarta linha tem as coordenadas menos 1, 1 e (menos 1, 1). A quinta linha tem as coordenadas 0, 0 e (0, 0). A sexta linha tem as coordenadas 1, 1 e (1, 1). A sétima linha tem as coordenadas 2, 4 e (2, 4). A sétima linha tem as coordenadas 3, 9 e (3, 9).

Exemplo\PageIndex{11}

Gráfico:f(x)=x^2.

Responda

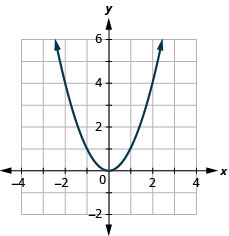
Essa figura tem um gráfico ao lado de uma tabela. No gráfico, há uma parábola que se abre representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 4 a 8. A parábola passa pelos pontos (menos 2, 4), (menos 1, 1), (0, 0), (1, 1) e (2, 4).

Exemplo\PageIndex{12}

f(x)=−x^2

Responda

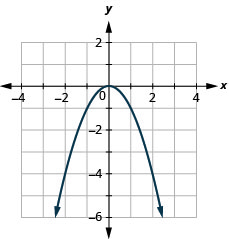
Essa figura tem um gráfico ao lado de uma tabela. No gráfico, há uma parábola que se abre representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 4 a 8. A parábola passa pelos pontos (menos 2, menos 4), (menos 1, menos 1), (0, 0), (1, menos 1) e (2, menos 4).

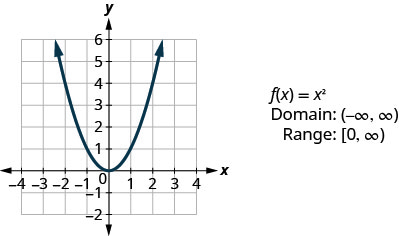
Observando o resultado em Exemplo, podemos resumir as características da função quadrada. Chamamos esse gráfico de parábola. Ao considerarmos o domínio, observe que qualquer número real pode ser usado como um valor x. O domínio é todo em números reais.

O intervalo não é todo em números reais. Observe que o gráfico consiste em valores de y nunca abaixo de zero. Isso faz sentido, pois o quadrado de qualquer número não pode ser negativo. Portanto, o intervalo da função quadrada é composto por todos números reais não negativos.

FUNÇÃO QUADRADA

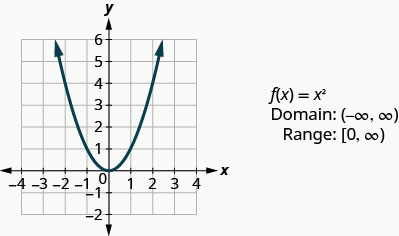
Esta figura tem um gráfico de uma parábola se abrindo representado graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 2 a 6. A parábola passa pelos pontos (menos 2, 4), (menos 1, 1), (0, 0), (1, 1) e (2, 4). Ao lado do gráfico estão os seguintes: “f de x é igual a x ao quadrado”, “Domínio: (infinito negativo, infinito)” e “Alcance: [0, infinito)”.

A próxima função que examinaremos também não é uma função linear, então o gráfico não será uma linha. Novamente, usaremos a plotagem de pontos e nos certificaremos de escolher vários valores positivos e negativos, bem como 0 para nossos valores x.

Gráfico:f(x)=x^3.

Responda

Nós escolhemos valores x. Nós os substituímos e, em seguida, criamos um gráfico.

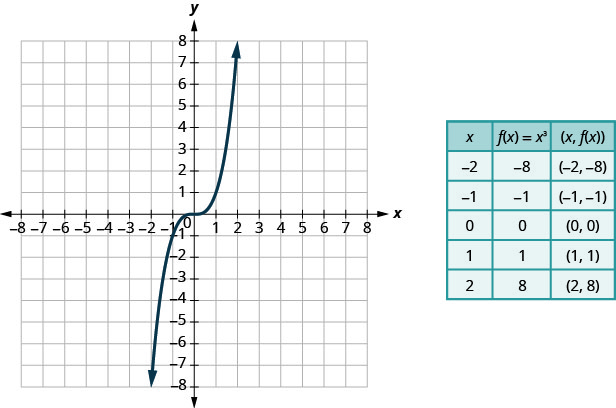
Esta figura tem uma linha curva representada graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 4 a 4. A linha curva passa pelos pontos (menos 2, menos 8), (menos 1, menos 1), (0, 0), (1, 1) e (2, 8). Ao lado do gráfico está uma tabela. A tabela tem 6 linhas e 3 colunas. A primeira linha é uma linha de cabeçalho com os cabeçalhos x, f de x iguais a x ao cubo e (x, f de x). A segunda linha tem as coordenadas menos 2, menos 8 e (menos 2, menos 8). A terceira linha tem as coordenadas menos 1, menos 1 e (menos 1, menos 1). A quarta linha tem as coordenadas 0, 0 e (0, 0). A quinta linha tem as coordenadas 1, 1 e (1, 1). A sexta linha tem as coordenadas 2, 8 e (2, 8).

Exemplo\PageIndex{14}

Gráfico:f(x)=x^3.

Responda

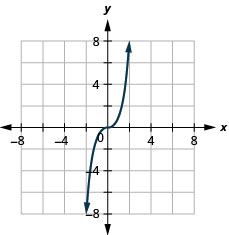
Esta figura tem uma linha curva representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha curva passa pelos pontos (menos 2, menos 8), (menos 1, menos 1), (0, 0), (1, 1) e (2, 8).

Exemplo\PageIndex{15}

Gráfico:f(x)=−x^3.

Responda

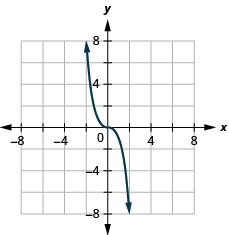
Esta figura tem uma linha curva representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha curva passa pelos pontos (menos 2, 8), (menos 1, 1), (0, 0), (1, menos 1) e (2, menos 8).

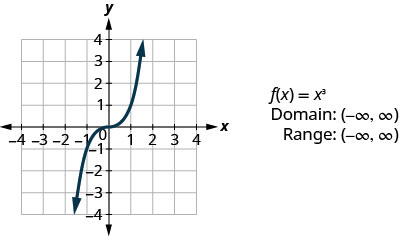
Analisando o resultado em Exemplo, podemos resumir as características da função de cubo. Ao considerarmos o domínio, observe que qualquer número real pode ser usado como um valor x. O domínio é todo em números reais.

O intervalo é todo em números reais. Isso faz sentido, pois o cubo de qualquer número diferente de zero pode ser positivo ou negativo. Portanto, o alcance da função de cubo é todo em números reais.

FUNÇÃO DE CUBO

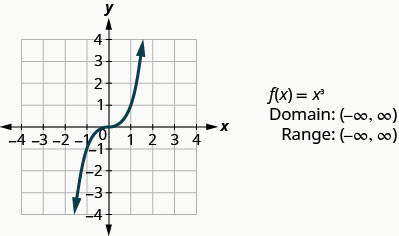
Esta figura tem uma linha curva representada graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 4 a 4. A linha curva passa pelos pontos (menos 2, menos 8), (menos 1, menos 1), (0, 0), (1, 1) e (2, 8).). Ao lado do gráfico estão os seguintes: “f de x é igual a x ao cubo”, “Domínio: (infinito negativo, infinito)” e “Alcance: (infinito negativo, infinito)”.

A próxima função que examinaremos não faz o quadrado nem o cubo dos valores de entrada, mas usa a raiz quadrada desses valores.

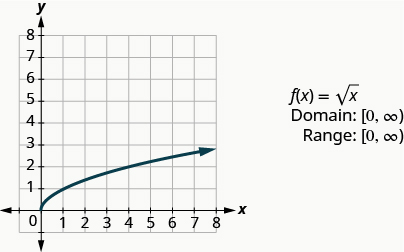
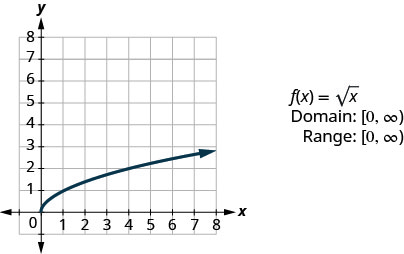
Vamos representar graficamente a funçãof(x)=\sqrt{x} e, em seguida, resumir as características da função. Lembre-se de que só podemos obter a raiz quadrada de números reais não negativos, então nosso domínio será os números reais não negativos.

Exemplo\PageIndex{16}

f(x)=\sqrt{x}

Responda

Nós escolhemos valores x. Como usaremos a raiz quadrada, escolhemos números que são quadrados perfeitos, para facilitar nosso trabalho. Nós os substituímos e, em seguida, criamos um gráfico.

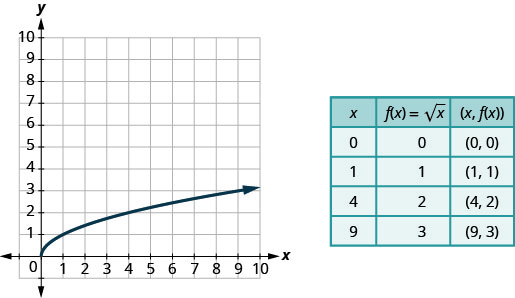
Esta figura tem uma meia linha curva representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 8. O eixo y vai de 0 a 8. A meia-linha curva começa no ponto (0, 0) e depois sobe e vai para a direita. A meia linha curva passa pelos pontos (1, 1) e (4, 2). Ao lado do gráfico está uma tabela. A tabela tem 5 linhas e 3 colunas. A primeira linha é uma linha de cabeçalho com os cabeçalhos x, f de x é igual à raiz quadrada de x e (x, f de x). A segunda linha tem as coordenadas 0, 0 e (0, 0). A terceira linha tem as coordenadas 1, 1 e (1, 1). A quarta linha tem as coordenadas 4, 2 e (4, 2). A quinta linha tem as coordenadas 9, 3 e (9, 3).

Exemplo\PageIndex{17}

Gráfico:f(x)=x.

Responda

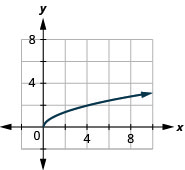
Esta figura tem uma meia linha curva representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 10. O eixo y vai de 0 a 10. A meia-linha curva começa no ponto (0, 0) e depois sobe e vai para a direita. A meia linha curva passa pelos pontos (1, 1), (4, 2) e (9, 3).

Exemplo\PageIndex{18}

Gráfico:f(x)=−\sqrt{x}.

Responda

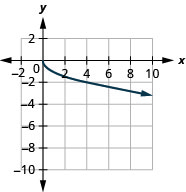
Esta figura tem uma meia linha curva representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 10. O eixo y vai de menos 10 a 0. A meia-linha curva começa no ponto (0, 0) e depois desce e para a direita. A meia linha curva passa pelos pontos (1, menos 1), (4, menos 2) e (9, menos 3).

FUNÇÃO DE RAIZ QUADRADA

Esta figura tem uma meia linha curva representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 8. O eixo y vai de 0 a 8. A meia-linha curva começa no ponto (0, 0) e depois sobe e vai para a direita. A meia linha curva passa pelos pontos (1, 1) e (4, 2). Ao lado do gráfico estão os seguintes: “f de x é igual à raiz quadrada de x”, “Domínio: [0, infinito)” e “Intervalo: [0, infinito)”.

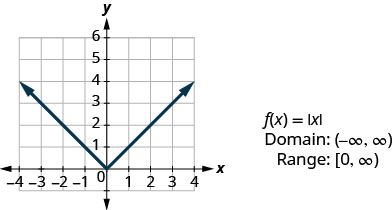
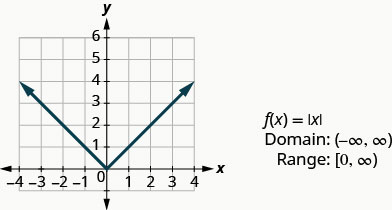
Nossa última função básica é a função de valor absoluto,f(x)=|x|. Lembre-se de que o valor absoluto de um número é sua distância de zero. Como nunca medimos a distância como um número negativo, nunca obteremos um número negativo na faixa.

Gráfico:f(x)=|x|.

Responda

Nós escolhemos valores x. Nós os substituímos e, em seguida, criamos um gráfico.

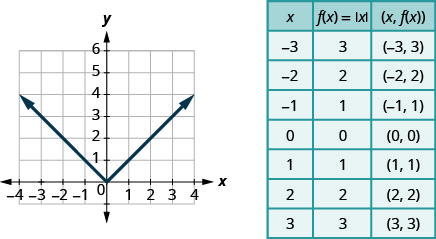
Esta figura tem uma linha em forma de v representada graficamente no plano de coordenadas x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 1 a 6. A linha em forma de v passa pelos pontos (menos 3, 3), (menos 2, 2), (menos 1, 1), (0, 0), (1, 1), (2, 2) e (3, 3). Ao lado do gráfico está uma tabela. A tabela tem 8 linhas e 3 colunas. A primeira linha é uma linha de cabeçalho com os cabeçalhos x, f de x é igual ao valor absoluto de x e (x, f de x). A segunda linha tem as coordenadas menos 3, 3 e (menos 3, 3). A terceira linha tem as coordenadas menos 2, 2 e (menos 2, 2). A quarta linha tem as coordenadas menos 1, 1 e (menos 1, 1). A quinta linha tem as coordenadas 0, 0 e (0, 0). A sexta linha tem as coordenadas 1, 1 e (1, 1). A sétima linha tem as coordenadas 2, 2 e (2, 2). A oitava linha tem as coordenadas 3, 3 e (3, 3).

Exemplo\PageIndex{20}

Gráfico:f(x)=|x|.

Responda

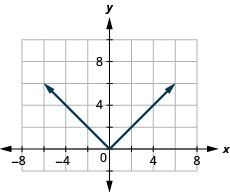
Esta figura tem uma linha em forma de v representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. A linha em forma de v passa pelos pontos (menos 3, 3), (menos 2, 2), (menos 1, 1), (0, 0), (1, 1), (2, 2) e (3, 3).

Exemplo\PageIndex{21}

Gráfico:f(x)=−|x|.

Responda

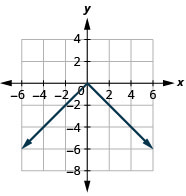
Esta figura tem uma linha em forma de v representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 8 a 4. A linha em forma de v passa pelos pontos (menos 3, menos 3), (menos 2, menos 2), (menos 1, menos 1), (0, 0), (1, menos 1), (2, menos 2) e (3, menos 3).

FUNÇÃO DE VALOR ABSOLUTO

Esta figura tem uma linha em forma de v representada graficamente no plano de coordenadas x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 1 a 6. A linha em forma de v passa pelos pontos (menos 3, 3), (menos 2, 2), (menos 1, 1), (0, 0), (1, 1), (2, 2) e (3, 3). O ponto (0, 0) em que a linha muda de inclinação é chamado de vértice. Ao lado do gráfico estão os seguintes: “f de x é igual ao valor absoluto de x”, “Domínio: (infinito negativo, infinito)” e “Alcance: [0, infinito)”.

Leia informações de um gráfico de uma função

Nas ciências e nos negócios, os dados geralmente são coletados e depois representados graficamente. O gráfico é analisado, as informações são obtidas do gráfico e, em seguida, muitas vezes as previsões são feitas a partir dos dados.

Começaremos lendo o domínio e o alcance de uma função em seu gráfico.

Lembre-se de que o domínio é o conjunto de todos os valores x nos pares ordenados na função. Para encontrar o domínio, examinamos o gráfico e encontramos todos os valores de x que têm um valor correspondente no gráfico. Siga o valor x para cima ou para baixo verticalmente. Se você clicar no gráfico da função, x estará no domínio.

Lembre-se de que o intervalo é o conjunto de todos os valores y nos pares ordenados na função. Para encontrar o intervalo, examinamos o gráfico e encontramos todos os valores de y que têm um valor correspondente no gráfico. Siga o valor y para a esquerda ou para a direita na horizontal. Se você acertar o gráfico da função, y estará no intervalo.

Exemplo\PageIndex{22}

Use o gráfico da função para encontrar seu domínio e alcance. Escreva o domínio e o intervalo em notação de intervalo.

Esta figura tem um segmento de linha curva representado graficamente no plano de coordenadas x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 4 a 4. O segmento de linha curva passa pelos pontos (menos 3, menos 1), (1,5, 3) e (3, 1). O intervalo [menos 3, 3] está marcado no eixo horizontal. O intervalo [menos 1, 3] está marcado no eixo vertical.

Responda

Para encontrar o domínio, examinamos o gráfico e encontramos todos os valores de x que correspondem a um ponto no gráfico. O domínio é destacado em vermelho no gráfico. O domínio é[−3,3].

Para encontrar o intervalo, examinamos o gráfico e encontramos todos os valores de y que correspondem a um ponto no gráfico. O intervalo é destacado em azul no gráfico. O alcance é[−1,3].

Exemplo\PageIndex{23}

Use o gráfico da função para encontrar seu domínio e alcance. Escreva o domínio e o intervalo em notação de intervalo.

Esta figura tem um segmento de linha curva representado graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. O segmento de linha curva passa pelos pontos (menos 5, menos 4), (0, menos 3) e (1, 2). O intervalo [menos 5, 1] está marcado no eixo horizontal. O intervalo [menos 4, 2] está marcado no eixo vertical.

Responda

O domínio é[−5,1]. O alcance é[−4,2].

Exemplo\PageIndex{24}

Use o gráfico da função para encontrar seu domínio e alcance. Escreva o domínio e o intervalo em notação de intervalo.

Esta figura tem um segmento de linha curva representado graficamente no plano de coordenadas x y. O eixo x vai de menos 4 a 5. O eixo y vai de menos 6 a 4. O segmento de linha curva passa pelos pontos (menos 2, 1), (0, 3) e (4, menos 5). O intervalo [menos 2, 4] está marcado no eixo horizontal. O intervalo [menos 5, 3] está marcado no eixo vertical.

Responda

O domínio é[−2,4]. O alcance é[−5,3].

Agora vamos ler as informações do gráfico que você poderá ver em futuras aulas de matemática.

Exemplo\PageIndex{25}

Use o gráfico da função para encontrar os valores indicados.

Esta figura tem uma linha curva ondulada representada graficamente no plano de coordenadas x y. O eixo x vai de menos 2 vezes pi a 2 vezes pi. O eixo y vai de menos 4 a 4. O segmento de linha curva passa pelos pontos (menos 2 vezes pi, 0), (menos 3 dividido por 2 vezes pi, 1), (pi negativo, 0), (menos 1 dividido por 2 vezes pi, negativo 1), (0, 0), (1 dividido por 2 vezes pi, 1), (pi, 0), (3 dividido por 2 vezes pi, menos 1) e (2 vezes pi, 0). Os pontos (menos 3 dividido por 2 vezes pi, 1) e (1 dividido por 2 vezes pi, 1) são os pontos mais altos no gráfico. Os pontos (menos 1 dividido por 2 vezes pi, menos 1) e (3 dividido por 2 vezes pi, menos 1) são os pontos mais baixos do gráfico. O padrão se estende infinitamente para a esquerda e para a direita.

ⓐ Encontre:f(0).
ⓑ Encontre:f(32\pi).
ⓒ Encontre:f(−12\pi).
ⓓ Encontre os valores para x quandof(x)=0.
ⓔ Encontre as interceptações x.
ⓕ Encontre as interceptações y.
ⓖ Encontre o domínio. Escreva-o em notação de intervalo.
ⓗ Encontre o alcance. Escreva-o em notação de intervalo.

Responda

ⓐ Quandox=0, a função cruza o eixo y em 0. Então,f(0)=0.
ⓑ Quandox=32\pi, o valor y da função é−1. Então,f(32\pi)=−1.
ⓒ Quandox=−12\pi, o valor y da função é−1. Então,f(−12\pi)=−1.
ⓓ A função é 0 nos pontos,(−2\pi,0), (−\pi,0), (0,0),(\pi,0),(2\pi,0). Os valores de x quandof(x)=0 são−2\pi,−\pi,0,\pi,2\pi.
ⓔ As interceptações x ocorrem quandoy=0. Portanto, as interceptações x ocorrem quandof(x)=0. Os interceptos x são(−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0).
ⓕ As interceptações y ocorrem quando x=0,x=0. Portanto, as interceptações y ocorrem emf(0). O intercepto y é(0,0).
ⓖ Essa função tem um valor quando x é de−2\pi para2\pi. Portanto, o domínio na notação de intervalo é[−2\pi,2\pi].
ⓗ Os valores desta função, ou valores de y, vão de 1−1 a 1. Portanto, o intervalo, em notação de intervalo, é[−1,1].

Exemplo\PageIndex{26}

Use o gráfico da função para encontrar os valores indicados.

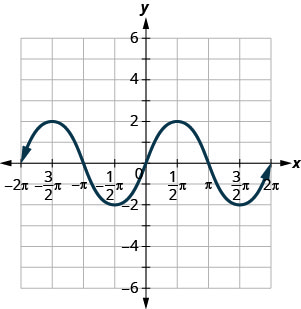
Esta figura tem uma linha curva ondulada representada graficamente no plano de coordenadas x y. O eixo x vai de menos 2 vezes pi a 2 vezes pi. O eixo y vai de menos 6 a 6. O segmento de linha curva passa pelos pontos (menos 2 vezes pi, 0), (menos 3 dividido por 2 vezes pi, 2), (pi negativo, 0), (menos 1 dividido por 2 vezes pi, negativo 2), (0, 0), (1 dividido por 2 vezes pi, 2), (pi, 0), (3 dividido por 2 vezes pi, menos 2) e (2 vezes pi, 0). Os pontos (menos 3 dividido por 2 vezes pi, 2) e (1 dividido por 2 vezes pi, 2) são os pontos mais altos no gráfico. Os pontos (menos 1 dividido por 2 vezes pi, menos 2) e (3 dividido por 2 vezes pi, menos 2) são os pontos mais baixos do gráfico. A linha se estende infinitamente para a esquerda e para a direita.

ⓐ Encontre: f (0) .f (0).
ⓑ Encontre: f (12\ pi) .f (12\ pi).
ⓒ Encontre: f (−32\ pi) .f (−32\ pi).
ⓓ Encontre os valores para x quando f (x) =0.f (x) =0.
ⓔ Encontre as interceptações x.
ⓕ Encontre as interceptações y.
ⓖ Encontre o domínio. Escreva-o em notação de intervalo.
ⓗ Encontre o alcance. Escreva-o em notação de intervalo.

Responda

ⓐf(0)=0 ⓑf=(\pi2)=2 ⓒf=(−3\pi2)=2 ⓓf(x)=0 parax=−2\pi,−\pi,0,\pi,2\pi ⓔ(−2\pi,0),(−\pi,0),(0,0),(\pi,0),(2\pi,0) ⓕ (0,0) (0,0) ⓖ[−2\pi,2\pi] ⓗ[−2,2]

Exemplo\PageIndex{27}

Use o gráfico da função para encontrar os valores indicados.

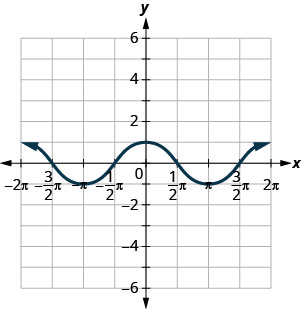
Esta figura tem uma linha curva ondulada representada graficamente no plano de coordenadas x y. O eixo x vai de menos 2 vezes pi a 2 vezes pi. O eixo y vai de menos 6 a 6. O segmento de linha curva passa pelos pontos (menos 2 vezes pi, 1), (menos 3 dividido por 2 vezes pi, 0), (pi negativo, menos 1), (menos 1 dividido por 2 vezes pi, 0), (0, 1), (1 dividido por 2 vezes pi, 0), (pi, menos 1), (3 dividido por 2 vezes pi, 0) e (2 vezes pi, 1). Os pontos (menos 2 vezes pi, 1), (0, 1) e (2 vezes pi, 1) são os pontos mais altos no gráfico. Os pontos (pi negativo, menos 1) e (pi, menos 1) são os pontos mais baixos do gráfico. O padrão se estende infinitamente para a esquerda e para a direita.

ⓐ Encontre:f(0).
ⓑ Encontre:f(\pi).
ⓒ Encontre:f(−\pi).
ⓓ Encontre os valores para x quandof(x)=0.
ⓔ Encontre as interceptações x.
ⓕ Encontre as interceptações y.
ⓖ Encontre o domínio. Escreva-o em notação de intervalo.
ⓗ Encontre o alcance. Escreva-o em notação de intervalo.

Responda

ⓐf(0)=1 ⓑf(\pi)=−1 ⓒf(−\pi)=−1 ⓓf(x)=0 parax=−3\pi2,−\pi2,\pi2,3\pi2 ⓔ(−2pi,0),(−pi,0),(0,0),(pi,0),(2pi,0) ⓕ(0,1) ⓖ[−2pi,2pi] ⓗ[−1,1]

Acesse esse recurso on-line para obter instruções e práticas adicionais com gráficos de funções.

Conceitos-chave

  • Teste de linha vertical
    • Um conjunto de pontos em um sistema de coordenadas retangulares é o gráfico de uma função se cada linha vertical cruzar o gráfico em no máximo um ponto.
    • Se alguma linha vertical cruzar o gráfico em mais de um ponto, o gráfico não representa uma função.
  • Gráfico de uma função
    • O gráfico de uma função é o gráfico de todos os seus pares ordenados, (x, y) (x, y) ou usando a notação da função, (x, f (x)) (x, f (x)) onde y=f (x) .y=f (x).

      fxf (x) nome da função-coordenada x da coordenada par ordenada do par ordenado fnome da funçãoxx-coordenada do par ordenado coordenada y do par ordenado

  • Função linear
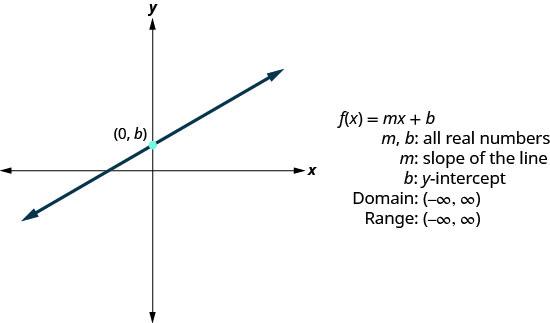
    Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. A linha passa pelo ponto (0, b). Ao lado do gráfico estão os seguintes: “f de x é igual a x mais b”, “m, b: todos os números reais”, “m: inclinação da linha”, “b: intercepto y”, “Domínio: (infinito negativo, infinito)” e “Alcance: (infinito negativo, infinito)”.
  • Função constante
    Esta figura tem um gráfico de uma linha reta horizontal no plano de coordenadas x y. A linha passa pelo ponto (0, b). Ao lado do gráfico estão os seguintes: “f de x é igual a sb”, “b: qualquer número real”, “b: intercepto y”, “Domínio: (infinito negativo, infinito)” e “Alcance: b”.
  • Função de identidade
    Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. A linha passa pelos pontos (0, 0), (1, 1) e (2, 2). Ao lado do gráfico estão os seguintes: “f de x é igual a x”, “m: 1”, “b: 0”, “Domínio: (infinito negativo, infinito)” e “Alcance: (infinito negativo, infinito)”.
  • Função quadrada
    Esta figura tem um gráfico de uma parábola se abrindo representado graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 2 a 6. A parábola passa pelos pontos (menos 2, 4), (menos 1, 1), (0, 0), (1, 1) e (2, 4). Ao lado do gráfico estão os seguintes: “f de x é igual a x ao quadrado”, “Domínio: (infinito negativo, infinito)” e “Alcance: [0, infinito)”.
  • Função Cube
    Esta figura tem uma linha curva representada graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 4 a 4. A linha curva passa pelos pontos (menos 2, menos 8), (menos 1, menos 1), (0, 0), (1, 1) e (2, 8).). Ao lado do gráfico estão os seguintes: “f de x é igual a x ao cubo”, “Domínio: (infinito negativo, infinito)” e “Alcance: (infinito negativo, infinito)”.
  • Função de raiz quadrada
    Esta figura tem uma meia linha curva representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 8. O eixo y vai de 0 a 8. A meia-linha curva começa no ponto (0, 0) e depois sobe e vai para a direita. A meia linha curva passa pelos pontos (1, 1) e (4, 2). Ao lado do gráfico estão os seguintes: “f de x é igual à raiz quadrada de x”, “Domínio: [0, infinito)” e “Intervalo: [0, infinito)”.
  • Função de valor absoluto
    Esta figura tem uma linha em forma de v representada graficamente no plano de coordenadas x y. O eixo x vai de menos 4 a 4. O eixo y vai de menos 1 a 6. A linha em forma de v passa pelos pontos (menos 3, 3), (menos 2, 2), (menos 1, 1), (0, 0), (1, 1), (2, 2) e (3, 3). O ponto (0, 0) em que a linha muda de inclinação é chamado de vértice. Ao lado do gráfico estão os seguintes: “f de x é igual ao valor absoluto de x”, “Domínio: (infinito negativo, infinito)” e “Alcance: [0, infinito)”.