1.5: Decimais
- Page ID
- 183398
Ao final desta seção, você poderá:
- Números decimais arredondados
- Adicione e subtraia números decimais
- Multiplique e divida decimais
- Converta números decimais, frações e porcentagens
- Simplifique expressões com raízes quadradas
- Identifique números inteiros, números racionais, números irracionais e números reais
- Localize frações e decimais na reta numérica
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Álgebra Elementar, Fundamentos.
Decimais arredondados
Os decimais são outra forma de escrever frações cujos denominadores são potências de dez.
\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]
Assim como em números inteiros, cada dígito de um decimal corresponde ao valor posicional com base nas potências de dez. A figura mostra os nomes dos valores posicionais à esquerda e à direita do ponto decimal.
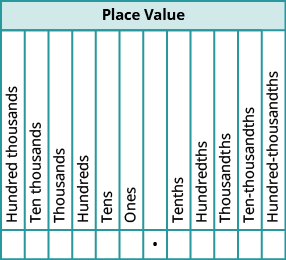
Quando trabalhamos com decimais, geralmente é necessário arredondar o número para o valor posicional necessário mais próximo. Resumimos as etapas para arredondar um decimal aqui.
- Localize o valor posicional fornecido e marque-o com uma seta.
- Sublinhe o dígito à direita do valor posicional.
- O dígito sublinhado é maior ou igual a 5?
- Sim: adicione 1 ao dígito no valor posicional fornecido.
- Não: não altere o dígito no valor posicional fornecido
- Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado.
Arredonde\(18.379\) para o número inteiro ⓐ centésimo ⓑ décimo ⓒ mais próximo.
- Resposta
-
Rodada\(18.379.\)
ⓐ até o centésimo mais próximo
Localize a posição dos centésimos com uma seta. 
Sublinhe o dígito à direita do valor posicional fornecido. 
Como 9 é maior ou igual a 5, adicione 1 ao 7. 
Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado. 
Observe que os dígitos excluídos NÃO foram substituídos por zeros. 
ⓑ até o décimo mais próximo
Localize o décimo lugar com uma flecha. 
Sublinhe o dígito à direita do valor posicional fornecido. 
Como 7 é maior ou igual a 5, adicione 1 ao 3. 
Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado. 
Observe que os dígitos excluídos NÃO foram substituídos por zeros. 
ⓒ para o número inteiro mais próximo
Localize o único lugar com uma flecha. 
Sublinhe o dígito à direita do valor posicional fornecido. 
Como 3 não é maior ou igual a 5, não adicione 1 ao 8. 
Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado. 

Arredonde\(6.582\) para o número inteiro ⓐ centésimo ⓑ décimo ⓒ mais próximo.
- Resposta
-
ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)
Arredonde\(15.2175\) para o mais próximo ⓐ milésimo ⓑ centésimo ⓒ décimo.
- Resposta
-
ⓐ\(15.218\) ⓑ\(15.22\)
ⓒ\(15.2\)
Adicionar e subtrair números decimais
Para somar ou subtrair decimais, alinhamos os pontos decimais. Ao alinhar os pontos decimais dessa forma, podemos somar ou subtrair os valores posicionais correspondentes. Em seguida, adicionamos ou subtraímos os números como se fossem números inteiros e colocamos o ponto decimal na soma.
- Determine o sinal da soma ou diferença.
- Escreva os números para que os pontos decimais se alinhem verticalmente.
- Use zeros como espaços reservados, conforme necessário.
- Adicione ou subtraia os números como se fossem números inteiros. Em seguida, coloque o ponto
decimal na resposta abaixo dos pontos decimais nos números fornecidos. - Escreva a soma ou a diferença com o sinal apropriado.
Adicione ou subtraia: ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)
- Resposta
-
ⓐ
\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)
ⓑ
\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)
Adicione ou subtraia: ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\).
- Resposta
-
ⓐ\(−16.49\) ⓑ\(−0.42\)
Adicione ou subtraia: ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\).
- Resposta
-
ⓐ\(−23.593\) ⓑ\(−12.58\)
Multiplique e divida números decimais
Quando multiplicamos decimais assinados, primeiro determinamos o sinal do produto e depois multiplicamos como se os números fossem positivos. Multiplicamos os números temporariamente ignorando o ponto decimal e depois contamos o número de pontos decimais nos fatores e essa soma nos informa o número de casas decimais no produto. Por fim, escrevemos o produto com o sinal apropriado.
- Determine o sinal do produto.
- Escreva em formato vertical, alinhando os números à direita. Multiplique os números como se fossem números inteiros, ignorando temporariamente os pontos decimais.
- Coloque o ponto decimal. O número de casas decimais no produto é a soma
do número de casas decimais nos fatores. - Escreva o produto com o sinal apropriado.
Multiplique:\((−3.9)(4.075)\).
- Resposta
-
\((−3.9)(4.075)\) Os sinais são diferentes. O produto
será negativo.O produto será negativo. Escreva em formato vertical, alinhando os
números à direita.
Multiplique. 
Adicione o número de casas decimais
nos fatores (1 + 3). Coloque o ponto decimal a 4 casas da direita.

Os sinais são diferentes, então o produto é negativo. \((−3.9)(4.075)=−15.8925\)
Multiplique:\(−4.5(6.107)\).
- Resposta
-
\(−27.4815\)
Multiplique:\(−10.79(8.12)\).
- Resposta
-
\(−87.6148\)
Freqüentemente, especialmente nas ciências, você multiplicará decimais por potências de 10 (10, 100, 1000, etc.). Se você multiplicar alguns produtos no papel, poderá notar um padrão relacionando o número de zeros na potência de 10 ao número de casas decimais. Movemos o ponto decimal para a direita para obter o produto.
- Mova o ponto decimal para a direita com o mesmo número de casas que o
número de zeros na potência de 10. - Adicione zeros no final do número conforme necessário.
Multiplique: 5,63 por ⓐ 10 ⓑ 100 ⓒ 1000.
- Resposta
-
Ao observar o número de zeros no múltiplo de dez, vemos o número de casas que precisamos mover o decimal para a direita.
ⓐ
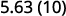
Há 1 zero em 10, então mova o ponto decimal 1 casa para a direita. 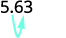
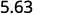
ⓑ
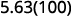
Há 2 zeros em 100, então mova o ponto decimal 2 casas para a direita. 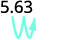

ⓒ
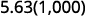
Há 3 zeros em 1.000, então mova a casa decimal 3 para a direita. 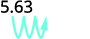
Um zero deve ser adicionado ao final. 
Multiplique 2,58 por ⓐ 10 ⓑ 100 ⓒ 1000.
- Resposta
-
ⓐ 25,8 ⓑ 258 ⓒ 2.580
Multiplique 14,2 por ⓐ 10 ⓑ 100 ⓒ 1000.
- Resposta
-
ⓐ 142 ⓑ 1.420 ⓒ 14.200
Assim como na multiplicação, a divisão de decimais assinados é muito parecida com a divisão de números inteiros. Só precisamos descobrir onde o ponto decimal deve ser colocado e o sinal do quociente. Ao dividir decimais assinados, primeiro determine o sinal do quociente e depois divida como se os números fossem positivos. Finalmente, escreva o quociente com o sinal apropriado.
Nós revisamos a notação e o vocabulário para divisão:

Escreveremos as etapas a serem seguidas ao dividir os decimais para facilitar a referência.
- Determine o sinal do quociente.
- Transforme o divisor em um número inteiro “movendo” o ponto decimal totalmente para a direita. “Mova” o ponto decimal no dividendo pelo mesmo número de casas, adicionando zeros conforme necessário.
- Divida. Coloque o ponto decimal no quociente acima do ponto decimal no dividendo.
- Escreva o quociente com o sinal apropriado.
Divida:\(−25.65÷(−0.06)\).
- Resposta
-
Lembre-se de que você pode “mover” os decimais no divisor e no dividendo por causa da Propriedade de Frações Equivalentes.
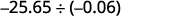
Os sinais são os mesmos. O quociente é positivo. Transforme o divisor em um número inteiro “movendo” o ponto decimal totalmente para a direita. “Mova” o ponto decimal no dividendo pelo mesmo número de casas. 
Divida. Coloque o ponto decimal no quociente acima do ponto decimal no dividendo. 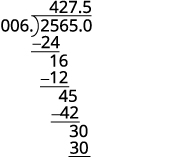
Escreva o quociente com o sinal apropriado. 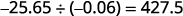
Divida:\(−23.492÷(−0.04)\).
- Resposta
-
\(587.3\)
Divida:\(−4.11÷(−0.12)\).
- Resposta
-
\(34.25\)
Converta números decimais, frações e porcentagens
Em nosso trabalho, muitas vezes é necessário mudar a forma de um número. Talvez tenhamos que transformar frações em decimais ou decimais em porcentagem.
Convertemos decimais em frações identificando o valor posicional do último dígito (mais à direita). No decimal 0,03. o 3 está na casa dos centésimos, então 100 é o denominador da fração equivalente a 0,03.
\[0.03=\dfrac{3}{100}\]
As etapas a serem seguidas para converter um decimal em uma fração estão resumidas na caixa de procedimento.
- Para converter um decimal em uma fração adequada, determine o valor posicional do dígito final.
- Escreva a fração.
- numerador—os “números” à direita do ponto decimal
- denominador — o valor posicional correspondente ao dígito final
- Para converter uma fração em decimal, divida o numerador da fração pelo denominador da fração.
Escreva: ⓐ\(0.374\) como uma fração ⓑ\(−\frac{5}{8}\) como decimal.
- Resposta
-
ⓐ
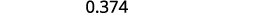
Determine o valor posicional do dígito final. 
Escreva a fração para 0,374: O numerador é 374. O denominador é 1.000. 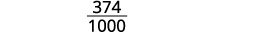
Simplifique a fração. 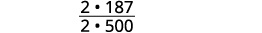
Divida os fatores comuns. 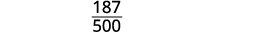
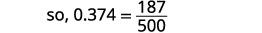
ⓑ Como uma barra fracionária significa divisão, começamos escrevendo a fração\(\frac{5}{8}\) como\(8\sqrt{5}\). Agora divida.
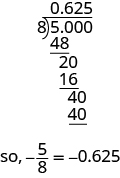
Escreva: ⓐ\(0.234\) como uma fração ⓑ\(−\frac{7}{8}\) como decimal.
- Resposta
-
ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)
Escreva: ⓐ\(0.024\) como uma fração ⓑ\(−\frac{3}{8}\) como decimal.
- Resposta
-
ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)
Uma porcentagem é uma proporção cujo denominador é 100. Porcentagem significa por cem. Usamos o símbolo de porcentagem,%, para mostrar a porcentagem. Como uma porcentagem é uma proporção, ela pode ser facilmente expressa como uma fração. Porcentagem significa por 100, então o denominador da fração é 100. Em seguida, alteramos a fração para um decimal dividindo o numerador pelo denominador. Depois de fazer isso várias vezes, você pode ver o padrão.
Para converter um número percentual em um número decimal, movemos o ponto decimal duas casas para a esquerda.
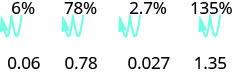
Para converter um decimal em um percentual, lembre-se de que porcentagem significa por cem. Se mudarmos o decimal para uma fração cujo denominador é 100, é fácil alterar essa fração para um percentual. Depois de muitas conversões, você pode reconhecer o padrão.
Para converter um decimal em porcentagem, movemos o ponto decimal duas casas para a direita e adicionamos o sinal de porcentagem.
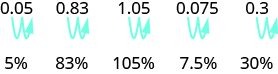
- Para converter uma porcentagem em decimal, mova o ponto decimal duas casas para a esquerda depois de remover o sinal de porcentagem.
- Para converter um decimal em porcentagem, mova o ponto decimal duas casas para a direita e adicione o sinal de porcentagem.
Converta cada um:
ⓐ porcentagem em decimal: 62%, 135% e 13,7%.
ⓑ decimal em um percentual: 0,51, 1,25 e 0,093.
- Resposta
-
ⓐ
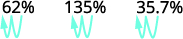
Mova o ponto decimal duas casas para a esquerda. 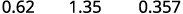
ⓑ
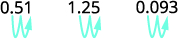
Mova o ponto decimal duas casas para a direita. 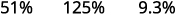
Converta cada um:
ⓐ porcentagem em decimal: 9%, 87% e 3,9%.
ⓑ decimal em um percentual: 0,17, 1,75 e 0,0825.
- Resposta
-
ⓐ 0,09, 0,87, 0,039 ⓑ 17%, 175%, 8,25%
Converta cada um:
ⓐ porcentagem em decimal: 3%, 91% e 8,3%.
ⓑ decimal em um percentual: 0,41, 2,25 e 0,0925.
- Resposta
-
ⓐ 0,03, 0,91, 0,083 ⓑ 41%, 225%, 9,25%
Simplifique expressões com raízes quadradas
Lembre-se de que quando um número\(n\) é multiplicado por si mesmo, nós o escrevemos\(n^2\) e lemos “\(n\)ao quadrado”. O resultado é chamado de quadrado de um número n. Por exemplo,\(\frac{8}{2}\) é lido como “8 ao quadrado” e 64 é chamado de quadrado de 8. Da mesma forma, 121 é o quadrado de 11 porque\(11^2\) é 121. Será útil aprender a reconhecer os números quadrados perfeitos.
Se\(n^2=m\), então m é o quadrado de n.
E quanto aos quadrados dos números negativos? Sabemos que quando os sinais de dois números são iguais, o produto deles é positivo. Portanto, o quadrado de qualquer número negativo também é positivo.
\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]
Porque\(10^2=100\), dizemos que 100 é o quadrado de 10. Também dizemos que 10 é uma raiz quadrada de 100. Um número cujo quadrado é m é chamado de raiz quadrada de um número m.
Se\(n^2=m\), então n é uma raiz quadrada de m.
Observe\((−10)^2=100\) também que −10 também é uma raiz quadrada de 100. Portanto, tanto 10 quanto −10 são raízes quadradas de 100. Então, todo número positivo tem duas raízes quadradas — uma positiva e uma negativa. O sinal radical,\(\sqrt{m}\), indica a raiz quadrada positiva. A raiz quadrada positiva é chamada de raiz quadrada principal. Quando usamos o sinal radical, isso sempre significa que queremos a raiz quadrada principal.
\(\sqrt{m}\)é lido como “a raiz quadrada de mm”.
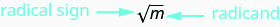
E se\(m=n^2\), então\(\sqrt{m}=n\), para\(n≥0\).
A raiz quadrada de m\(\sqrt{m}\),, é o número positivo cujo quadrado é m.
Sabemos que todo número positivo tem duas raízes quadradas e o sinal radical indica o positivo. Nós escrevemos\(\sqrt{100}=10\). Se quisermos encontrar a raiz quadrada negativa de um número, colocamos um negativo na frente do sinal radical. Por exemplo,\(−\sqrt{100}=−10\). Lemos\(−\sqrt{100}\) como “o oposto da raiz quadrada principal de 10”.
Simplifique: ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\).
- Resposta
-
ⓐ
\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)ⓑ
\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)
ⓒ
\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)
Simplifique: ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)
- Resposta
-
ⓐ 6 ⓑ 13 ⓒ −15
Simplifique: ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)
- Resposta
-
ⓐ 4 ⓑ 14 ⓒ −10
Identifique números inteiros, números racionais, números irracionais e números reais
Já descrevemos números como números de contagem s, números inteiros s e números inteiros. Qual é a diferença entre esses tipos de números? A diferença pode ser confundida com a subtração. Que tal perguntar como distinguimos esses tipos de números?
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]
Que tipo de números obteríamos se começássemos com todos os inteiros e depois incluíssemos todas as frações? Os números que teríamos formam o conjunto de números racionais. Um número racional é um número que pode ser escrito como uma proporção de dois inteiros.
Em geral, qualquer decimal que termine após um número de dígitos (como 7,3 ou −1,2684) é um número racional. Podemos usar o valor posicional do último dígito como denominador ao escrever o decimal como uma fração. O decimal para\(\frac{1}{3}\) é o número\(0.\overline{3}\). A barra acima do 3 indica que o número 3 se repete infinitamente. Continuamente tem um significado importante no cálculo. Os números abaixo da barra são chamados de bloco de repetição e se repetem continuamente.
Como todos os números inteiros podem ser escritos como uma fração cujo denominador é 1, os inteiros (e também a contagem e os números inteiros) são números racionais.
Todo número racional pode ser escrito como uma proporção de números inteiros\(\frac{p}{q}\), onde p e q são números inteiros e\(q≠0\), e como um decimal que para ou se repete.
Um número racional é um número da forma\(\frac{p}{q}\), onde p e q são números inteiros\(q≠0\) e.
Sua forma decimal para ou se repete.
Existem números decimais que não param nem se repetem? Sim! O número π (a letra grega pi, pronunciada “torta”), que é muito importante na descrição de círculos, tem uma forma decimal que não para nem se repete. Usamos três pontos (...) para indicar que o decimal não para nem se repete.
\[π=3.141592654...\]
A raiz quadrada de um número que não é um quadrado perfeito é um decimal que não para nem se repete.
Um número cuja forma decimal não para ou se repete não pode ser escrito como uma fração de números inteiros. Chamamos isso de número irracional.
Um número irracional é um número que não pode ser escrito como a proporção de dois inteiros.
Sua forma decimal não para e não se repete.
Vamos resumir um método que podemos usar para determinar se um número é racional ou irracional.
Se a forma decimal de um número
- repete ou pára, o número é um número racional.
- não se repete e não para, o número é um número irracional.
Vimos que todos os números contados são números inteiros, todos os números inteiros são números inteiros e todos os números inteiros são números racionais. Os números irracionais são números cuja forma decimal não para e não se repete. Quando juntamos os números racionais e os números irracionais, obtemos o conjunto dos números reais s.
Um número real é um número racional ou irracional.
Posteriormente neste curso, apresentaremos números além dos números reais. A figura ilustra como os conjuntos de números que usamos até agora se encaixam.
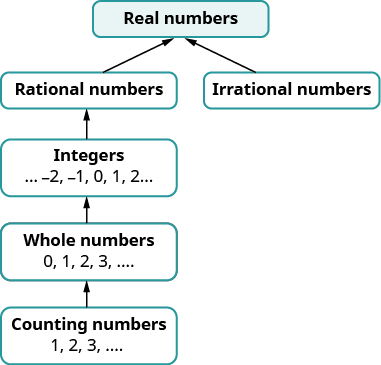
O termo “números reais” parece estranho para você? Existem números que não sejam “reais” e, em caso afirmativo, quais poderiam ser? Podemos simplificar\(−\sqrt{25}\)? Existe um número cujo quadrado é\(−25\)?
\[()^2=−25?\]
Nenhum dos números com os quais lidamos até agora tem um quadrado que seja\(−25\). Por quê? Qualquer número positivo ao quadrado é positivo. Qualquer número negativo ao quadrado é positivo. Então, dizemos que não há um número real igual\(\sqrt{−25}\) a. A raiz quadrada de um número negativo não é um número real.
Dados os números\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\), liste os ⓐ números inteiros ⓑ inteiros ⓒ números racionais ⓓ números irracionais ⓔ números reais.
- Resposta
-
ⓐ Lembre-se de que os números inteiros são\(0,1,2,3,…,\), então 8 é o único número inteiro fornecido.
ⓑ Os números inteiros são os números inteiros e seus opostos (o que inclui 0). Portanto, o número inteiro 8 é um número inteiro e −7 é o oposto de um número inteiro, então também é um número inteiro. Além disso, observe que 64 é o quadrado de 8 então\(−\sqrt{64}=−8\). Então, os números inteiros são\(−7,8,\)\(−\sqrt{64}\) e.
ⓒ Como todos os números inteiros são racionais, então\(−7,8,\) e\(−\sqrt{64}\) são racionais. Os números racionais também incluem frações e decimais que se repetem ou param, portanto\(\frac{14}{5}\) e\(5.9\) são racionais. Portanto, a lista de números racionais é\(−7,\frac{14}{5},8,5.9,\)\(−\sqrt{64}\) e.
ⓓ Lembre-se de que 5 não é um quadrado perfeito, então\(\sqrt{5}\) é irracional.
ⓔ Todos os números listados são números reais.
Dados os números,\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\) liste os ⓐ números inteiros ⓑ inteiros ⓒ números racionais
ⓓ números irracionais ⓔ números reais.
- Resposta
-
ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)
ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
Os números fornecidos\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\) listam os ⓐ números inteiros ⓑ inteiros ⓒ números racionais ⓓ números irracionais ⓔ números reais.
- Resposta
-
ⓐ\(6,\sqrt{121}\)
ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)
ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
ⓓ\(2.041975...\)
ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
Localize frações e decimais na reta numérica
Agora queremos incluir frações e decimais na reta numérica. Vamos começar com frações e localizar\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\) e\(\frac{8}{3}\) na reta numérica.
Começaremos com os números inteiros 3 e −5 porque eles são os mais fáceis de traçar. Veja a Figura.
As frações corretas listadas são\(\frac{1}{5}\) e\(−\frac{4}{5}.\) sabemos que a fração adequada\(\frac{1}{5}\) tem valor menor que um e, portanto, estaria localizada entre 0 e 1. O denominador é 5, então dividimos a unidade de 0 a 1 em 5 partes iguais\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). Nós planejamos\(\frac{1}{5}\).
Da mesma forma,\(−\frac{4}{5}\) está entre 0 e −1. Depois de dividir a unidade em 5 partes iguais, traçamos\(−\frac{4}{5}\).
Finalmente, veja as frações impróprias\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). Localizar esses pontos pode ser mais fácil se você alterar cada um deles para um número misto.
\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]
A figura mostra a reta numérica com todos os pontos traçados.

Localize e rotule o seguinte em uma linha numérica:\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\)\(\frac{7}{3}\) e.
- Resposta
-
Localize e plote os números inteiros,\(4,−3.\)
Localize\(\frac{3}{4}\) primeiro a fração adequada. A fração\(\frac{3}{4}\) está entre 0 e 1. Divida a distância entre 0 e 1 em quatro partes iguais e, em seguida, traçamos\(\frac{3}{4}\). Trama semelhante\(−\frac{1}{4}\).
Agora localize as frações impróprias\(\frac{6}{5},−\frac{5}{2},\)\(\frac{7}{3}\) e. É mais fácil plotá-los se os convertermos em números mistos e depois plotá-los conforme descrito acima:\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

Localize e rotule o seguinte em uma linha numérica:\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).
- Resposta
-
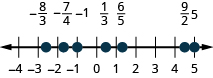
Localize e rotule o seguinte em uma linha numérica:\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).
- Resposta
-
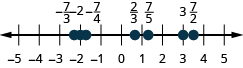
Como decimais são formas de frações, localizar decimais na reta numérica é semelhante à localização de frações na reta numérica.
Localize na reta numérica: ⓐ 0,4 ⓑ −0,74.
- Resposta
-
ⓐ O número decimal 0,4 é equivalente a\(\frac{4}{10}\) uma fração própria, então 0,4 está localizado entre 0 e 1. Em uma reta numérica, divida o intervalo entre 0 e 1 em 10 partes iguais. Agora identifique as peças 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9, 1,0. Escrevemos 0 como 0,0 e 1 como 1,0, para que os números estejam consistentemente em décimos. Finalmente, marque 0,4 na linha numérica.

ⓑ O decimal\(−0.74\) é equivalente a\(−\frac{74}{100}\), então está localizado entre 0 e .−1. Em uma reta numérica, marque e rotule os centésimos no intervalo entre 0 e −1.

Localize na linha numérica: ⓐ\(0.6\) ⓑ\(−0.25.\)
- Resposta
-
ⓐ

ⓑ
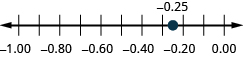
Localize na reta numérica: ⓐ 0,90,9 ⓑ −0,75.−0,75.
- Resposta
-
ⓐ

ⓑ
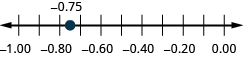
Acesse esse recurso on-line para obter instruções adicionais e praticar com decimais.
- Fundamentos da aritmética: divisão de números decimais
Conceitos-chave
- Como arredondar decimais.
- Localize o valor posicional fornecido e marque-o com uma seta.
- Sublinhe o dígito à direita do valor posicional.
- O dígito sublinhado é maior ou igual a 5?
- Sim: adicione 1 ao dígito no valor posicional fornecido.
- Não: não altere o dígito no valor posicional fornecido
- Reescreva o número, excluindo todos os dígitos à direita do dígito arredondado.
- Como adicionar ou subtrair números decimais.
- Determine o sinal da soma ou diferença.
- Escreva os números para que os pontos decimais se alinhem verticalmente.
- Use zeros como espaços reservados, conforme necessário.
- Adicione ou subtraia os números como se fossem números inteiros. Em seguida, coloque o ponto decimal na resposta abaixo dos pontos decimais nos números fornecidos.
- Escreva a soma ou a diferença com o sinal apropriado
- Como multiplicar números decimais.
- Determine o sinal do produto.
- Escreva em formato vertical, alinhando os números à direita. Multiplique os números como se fossem números inteiros, ignorando temporariamente os pontos decimais.
- Coloque o ponto decimal. O número de casas decimais no produto é a soma do número de casas decimais nos fatores.
- Escreva o produto com o sinal apropriado.
- Como multiplicar um decimal por uma potência de dez.
- Mova o ponto decimal para a direita com o mesmo número de casas que o número de zeros na potência de 10.
- Adicione zeros no final do número conforme necessário.
- Como dividir números decimais.
- Determine o sinal do quociente.
- Transforme o divisor em um número inteiro “movendo” o ponto decimal totalmente para a direita. “Mova” o ponto decimal no dividendo pelo mesmo número de casas, adicionando zeros conforme necessário.
- Divida. Coloque o ponto decimal no quociente acima do ponto decimal no dividendo.
- Escreva o quociente com o sinal apropriado.
- Como converter um decimal em uma fração própria e uma fração em um decimal.
- Para converter um decimal em uma fração adequada, determine o valor posicional do dígito final.
- Escreva a fração.
- numerador—os “números” à direita do ponto decimal
- denominador — o valor posicional correspondente ao dígito final
- Para converter uma fração em decimal, divida o numerador da fração pelo denominador da fração.
- Como converter um percentual em decimal e um decimal em porcentagem.
- Para converter uma porcentagem em decimal, mova o ponto decimal duas casas para a esquerda depois de remover o sinal de porcentagem.
- Para converter um decimal em porcentagem, mova o ponto decimal duas casas para a direita e adicione o sinal de porcentagem.
- A notação de raiz quadrada\(\sqrt{m}\) é lida como “a raiz quadrada de m”. E se\(m=n^2\), então\(\sqrt{m}=n\), para\(n≥0\). A raiz quadrada de m\(\sqrt{m}\),, é o número positivo cujo quadrado é m.
- Racional ou irracional Se a forma decimal de um número
- repete ou pára, o número é um número racional.
- não se repete e não para, o número é um número irracional.
- Números reais
.jpg)
Figura 4.
Glossário
- número irracional
- Um número irracional é um número que não pode ser escrito como a proporção de dois inteiros. Sua forma decimal não para e não se repete.
- por cento
- Uma porcentagem é uma proporção cujo denominador é 100.
- raiz quadrada principal
- A raiz quadrada positiva é chamada de raiz quadrada principal.
- número racional
- Um número racional é um número da forma\(\frac{p}{q}\), onde p e q são números inteiros\(q≠0\) e. Sua forma decimal para ou se repete.
- número real
- Um número real é um número que é racional ou irracional.
- quadrado de um número
- Se\(n^2=m\), então m é o quadrado de n.
- raiz quadrada de um número
- Se\(n^2=m\), então n é uma raiz quadrada de m.


