Skip to main content
Global

1.4E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183341

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Simplifique as frações

    Nos exercícios a seguir, simplifique.

    1. \(−\dfrac{108}{63}\)

    Responda

    \(−\dfrac{12}{7}\)

    2. \(−\dfrac{104}{48}\)

    3. \(\dfrac{120}{252}\)

    Responda

    \(\dfrac{10}{21}\)

    4. \(\dfrac{182}{294}\)

    5. \(\dfrac{14x^2}{21y}\)

    Responda

    \(\dfrac{2x^2}{3y}\)

    6. \(\dfrac{24a}{32b^2}\)

    7. \(−\dfrac{210a^2}{110b^2}\)

    Responda

    \(−\dfrac{21a^2}{11b^2}\)

    8. \(−\dfrac{30x^2}{105y^2}\)

    Multiplique e divida frações

    Nos exercícios a seguir, execute a operação indicada.

    9. \(−\dfrac{3}{4}\left(−\dfrac{4}{9}\right)\)

    Responda

    \(\dfrac{1}{3}\)

    10. \(−\dfrac{3}{8}⋅\dfrac{4}{15}\)

    11. \(\left(−\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)\)

    Responda

    \(−\dfrac{21}{50}\)

    12. \(\left(−\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)\)

    13. \(\left(−\dfrac{63}{84}\right)\left(−\dfrac{44}{90}\right)\)

    Responda

    \(\dfrac{11}{30}\)

    14. \(\left(−\dfrac{33}{60}\right)\left(−\dfrac{40}{88}\right)\)

    15. \(\dfrac{3}{7}⋅21n\)

    Responda

    \(9n\)

    16. \(\dfrac{5}{6}⋅30m\)

    17. \(\dfrac{3}{4}÷\dfrac{x}{11}\)

    Responda

    \(\dfrac{33}{4x}\)

    18. \(\dfrac{2}{5}÷\dfrac{y}{9}\)

    19. \(\dfrac{5}{18}÷\left(−\dfrac{15}{24}\right)\)

    Responda

    \(−\dfrac{4}{9}\)

    20. \(\dfrac{7}{18}÷\left(−\dfrac{14}{27}\right)\)

    21. \(\dfrac{8u}{15}÷\dfrac{12v}{25}\)

    Responda

    \(\dfrac{10u}{9v}\)

    22. \(\dfrac{12r}{25}÷\dfrac{18s}{35}\)

    23. \(\dfrac{3}{4}÷(−12)\)

    Responda

    \(−\dfrac{1}{16}\)

    24. \(−15÷\left(−\dfrac{5}{3}\right)\)

    Nos exercícios a seguir, simplifique.

    25. \(−\dfrac{\dfrac{8}{21} }{\dfrac{12}{35}}\)

    Responda

    \(−\dfrac{10}{9}\)

    26. \(− \dfrac{\dfrac{9}{16} }{\dfrac{33}{40}}\)

    27. \(−\dfrac{\dfrac{4}{5}}{2}\)

    Responda

    \(−\dfrac{2}{5}\)

    28. \(\dfrac{\dfrac{5}{3}}{10}\)

    29. \(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)

    Responda

    \(\dfrac{2m}{3n}\)

    30. \(\dfrac{−\dfrac{3}{8}}{−\dfrac{y}{12}}\)

    Adicionar e subtrair frações

    Nos exercícios a seguir, adicione ou subtraia.

    31. \(\dfrac{7}{12}+\dfrac{5}{8}\)

    Responda

    \(\dfrac{29}{24}\)

    32. \(\dfrac{5}{12}+\dfrac{3}{8}\)

    33. \(\dfrac{7}{12}−\dfrac{9}{16}\)

    Responda

    \(\dfrac{1}{48}\)

    34. \(\dfrac{7}{16}−\dfrac{5}{12}\)

    35. \(−\dfrac{13}{30}+\dfrac{25}{42}\)

    Responda

    \(\dfrac{17}{105}\)

    36. \(−\dfrac{23}{30}+\dfrac{5}{48}\)

    37. \(−\dfrac{39}{56}−\dfrac{22}{35}\)

    Responda

    \(−\dfrac{53}{40}\)

    38. \(−\dfrac{33}{49}−\dfrac{18}{35}\)

    39. \(−\dfrac{2}{3}−\left(−\dfrac{3}{4}\right)\)

    Responda

    \(\dfrac{1}{12}\)

    40. \(−\dfrac{3}{4}−\left(−\dfrac{4}{5}\right)\)

    41. \(\dfrac{x}{3}+\dfrac{1}{4}\)

    Responda

    \(\dfrac{4x+3}{12}\)

    42. \(\dfrac{x}{5}−\dfrac{1}{4}\)

    43. ⓐ\(\dfrac{2}{3}+\dfrac{1}{6}\)

    ⓑ\(\dfrac{2}{3}÷\dfrac{1}{6}\)

    Responda

    ⓐ\(\dfrac{5}{6}\) ⓑ\(4\)

    44. ⓐ\(−\dfrac{2}{5}−\dfrac{1}{8}\)

    ⓑ\(−\dfrac{2}{5}·\dfrac{1}{8}\)

    45. ⓐ\(\dfrac{5n}{6}÷\dfrac{8}{15}\)

    ⓑ\(\dfrac{5n}{6}−\dfrac{8}{15}\)

    Responda

    ⓐ\(\dfrac{25n}{16}\) ⓑ\(\dfrac{25n−16}{30}\)

    46. ⓐ\(\dfrac{3a}{8}÷\dfrac{7}{12}\)

    ⓑ\(\dfrac{3a}{8}−\dfrac{7}{12}\)

    47. ⓐ\(−\dfrac{4x}{9}−\dfrac{5}{6}\)

    ⓑ\(−\dfrac{4k}{9}⋅\dfrac{5}{6}\)

    Responda

    ⓐ\(\dfrac{−8x−15}{18}\) ⓑ\(−\dfrac{10k}{27}\)

    48. ⓐ\(−\dfrac{3y}{8}−\dfrac{4}{3}\)

    ⓑ\(−\dfrac{3y}{8}⋅\dfrac{4}{3}\)

    49. ⓐ\(−\dfrac{5a}{3}+\left(−\dfrac{10}{6}\right)\)

    ⓑ\(−\dfrac{5a}{3}÷\left(−\dfrac{10}{6}\right)\)

    Responda

    ⓐ\(\dfrac{−5(a+1)}{3}\) ⓑ\(a\)

    50. ⓐ\(\dfrac{2b}{5}+\dfrac{8}{15}\)

    ⓑ\(\dfrac{2b}{5}÷\dfrac{8}{15}\)

    Use a ordem das operações para simplificar as frações

    Nos exercícios a seguir, simplifique.

    51. \(\dfrac{5⋅6−3⋅4}{4⋅5−2⋅3}\)

    Responda

    \(\dfrac{9}{7}\)

    52. \(\dfrac{8⋅9−7⋅6}{5⋅6−9⋅2}\)

    53. \(\dfrac{5^2−3^2}{3−5}\)

    Responda

    \(−8\)

    54. \(\dfrac{6^2−4^2}{4−6}\)

    55. \(\dfrac{7⋅4−2(8−5)}{9⋅3−3⋅5}\)

    Responda

    \(\dfrac{11}{6}\)

    56. \(\dfrac{9⋅7−3(12−8)}{8⋅7−6⋅6}\)

    57. \(\dfrac{9(8−2)−3(15−7)}{6(7−1)−3(17−9)}\)

    Responda

    \(\dfrac{5}{2}\)

    58. \(\dfrac{8(9−2)−4(14−9)}{7(8−3)−3(16−9)}\)

    59. \(\dfrac{2^3+4^2}{\left(\dfrac{2}{3}\right)^2}\)

    Resposta

    \(54\)

    60. \(\dfrac{3^3−3^2}{\left(\dfrac{3}{4}\right)^2}\)

    61. \(\dfrac{\left(\dfrac{3}{5}\right)^2}{\left(\dfrac{3}{7}\right)^2}\)

    Resposta

    \(\dfrac{49}{25}\)

    62. \(\dfrac{\left(\dfrac{3}{4}\right)^2}{\left(\dfrac{5}{8}\right)^2}\)

    63. \(\dfrac{2}{\dfrac{1}{3}+\dfrac{1}{5}}\)

    Resposta

    \(\dfrac{15}{4}\)

    64. \(\dfrac{5}{\dfrac{1}{4}+\dfrac{1}{3}}\)

    65. \(\dfrac{\dfrac{7}{8}−\dfrac{2}{3}}{\dfrac{1}{2}+\dfrac{3}{8}}\)

    Resposta

    \(\dfrac{5}{21}\)

    66. \(\dfrac{\dfrac{3}{4}−\dfrac{3}{5}}{\dfrac{1}{4}+\dfrac{2}{5}}\)

    Prática m

    Nos exercícios a seguir, simplifique.

    67. \(−\dfrac{3}{8}÷\left(−\dfrac{3}{10}\right)\)

    Resposta

    \(\dfrac{5}{4}\)

    68. \(−\dfrac{3}{12}÷\left(−\dfrac{5}{9}\right)\)

    69. \(−\dfrac{3}{8}+\dfrac{5}{12}\)

    Resposta

    \(\dfrac{1}{24}\)

    70. \(−\dfrac{1}{8}+\dfrac{7}{12}\)

    71. \(−\dfrac{7}{15}−\dfrac{y}{4}\)

    Resposta

    \(\dfrac{−28−15y}{60}\)

    72. \(−\dfrac{3}{8}−\dfrac{x}{11}\)

    73. \(\dfrac{11}{12a}⋅\dfrac{9a}{16}\)

    Resposta

    \(\dfrac{33}{64}\)

    74. \(\dfrac{10y}{13}⋅\dfrac{8}{15y}\)

    75. \(\dfrac{1}{2}+\dfrac{2}{3}⋅\dfrac{5}{12}\)

    Resposta

    \(\dfrac{7}{9}\)

    76. \(\dfrac{1}{3}+\dfrac{2}{5}⋅\dfrac{3}{4}\)

    77. \(1−\dfrac{3}{5}÷\dfrac{1}{10}\)

    Resposta

    \(−5\)

    78. \(1−\dfrac{5}{6}÷\dfrac{1}{12}\)

    79. \(\dfrac{3}{8}−\dfrac{1}{6}+\dfrac{3}{4}\)

    Resposta

    \(\dfrac{23}{24}\)

    80. \(\dfrac{2}{5}+\dfrac{5}{8}−\dfrac{3}{4}\)

    81. \(12\left(\dfrac{9}{20}−\dfrac{4}{15}\right)\)

    Resposta

    \(\dfrac{11}{5}\)

    82. \(8\left(\dfrac{15}{16}−\dfrac{5}{6}\right)\)

    83. \(\dfrac{\dfrac{5}{8}+\dfrac{1}{6}}{\dfrac{19}{24}}\)

    Resposta

    \(1\)

    84. \(\dfrac{\dfrac{1}{6}+\dfrac{3}{10}}{\dfrac{14}{30}}\)

    ​​​​​​​

    85. \(\left(\dfrac{5}{9}+\dfrac{1}{6}\right)÷\left(\dfrac{2}{3}−\dfrac{1}{2}\right)\)

    Resposta

    \(\dfrac{13}{3}\)

    86. \(\left(\dfrac{3}{4}+\dfrac{1}{6}\right)÷\left(\dfrac{5}{8}−\dfrac{1}{3}\right)\)

    Avalie expressões variáveis com frações

    Nos exercícios a seguir, avalie.

    87. \(\dfrac{7}{10}−w\)quando ⓐ\(w=\dfrac{1}{2}\) ⓑ\(w=−\dfrac{1}{2}\)

    Resposta

    ⓐ\(\dfrac{1}{5}\) ⓑ\(\dfrac{6}{5}\)

    88. \(512−w\)quando ⓐ\(w=\dfrac{1}{4}\) ⓑ\(w=−\dfrac{1}{4}\)

    ​​​​​​​​​​​​​​

    89. \(2x^2y^3\)quando\(x=−\dfrac{2}{3}\) e\(y=−\dfrac{1}{2}\)

    Resposta

    \(−\dfrac{1}{9}\)

    90. \(8u^2v^3\)quando\(u=−\dfrac{3}{4}\) e\(v=−\dfrac{1}{2}\)

    ​​​​​​​​​​​​​​

    91. \(\dfrac{a+b}{a−b}\)quando\(a=−3\) e\(b=8\)

    Resposta

    \(−\dfrac{5}{11}\)

    92. \(\dfrac{r−s}{r+s}\)quando\(r=10\) e\(s=−5\)

    exercícios de escrita

    93. Por que você precisa de um denominador comum para somar ou subtrair frações? Explique.

    Resposta

    As respostas podem variar.

    94. Como você encontra o LCD de 2 frações?

    95. Explique como você encontra o recíproco de uma fração.

    Resposta

    As respostas podem variar.

    96. Explique como você encontra o inverso de um número negativo.

    Verificação automática

    ⓐ Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

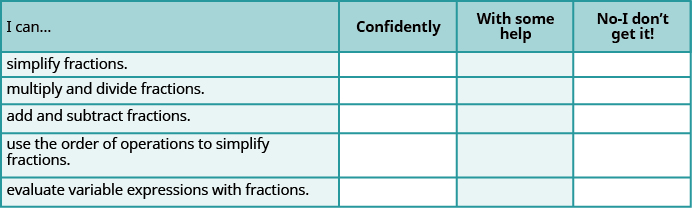
    Essa tabela tem 4 colunas, 5 linhas e uma linha de cabeçalho. A linha do cabeçalho rotula cada coluna que eu posso, com confiança, com alguma ajuda e não, eu não entendo. A primeira coluna tem as seguintes afirmações: simplificar frações, multiplicar e dividir frações, adicionar e subtrair frações, usar a ordem das operações para simplificar frações, avaliar expressões variáveis com frações. As colunas restantes estão em branco.

    ⓑ O que essa lista de verificação diz sobre seu domínio desta seção? Quais etapas você tomará para melhorar?