1.4: Frações
- Page ID
- 183325
Ao final desta seção, você poderá:
- Simplifique frações
- Multiplique e divida frações
- Adicionar e subtrair frações
- Use a ordem das operações para simplificar as frações
- Avalie expressões variáveis com frações
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Álgebra Elementar, Fundamentos.
Simplifique as frações
Uma fração é uma forma de representar partes de um todo. A fração\(\frac{2}{3}\) representa duas das três partes iguais (Figura\(\PageIndex{1}\)). Na fração\(\frac{2}{3}\), o 2 é chamado de numerador e o 3 é chamado de denominador. A linha é chamada de barra de fração.
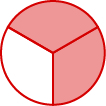
Figura\(\PageIndex{1}\): No círculo,\(\frac{2}{3}\) o círculo está sombreado — 2 das 3 partes iguais.
Uma fração é escrita\(\dfrac{a}{b}\), onde\(b\neq 0\) e
\(a\)é o numerador e\(b\) é o denominador.
Uma fração representa partes de um todo. O denominador\(b\) é o número de partes iguais em que o todo foi dividido e o numerador\(a\) indica quantas partes estão incluídas.
Frações que têm o mesmo valor são frações equivalentes. As frações equivalentes
A propriedade nos permite encontrar frações equivalentes e também simplificar frações.
Se\(a\)\(b\), e\(c\) são números em que\(b\neq 0,c\neq 0\),
em seguida,\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) e\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
Uma fração é considerada simplificada se não houver fatores comuns, além de 1, em seu numerador e denominador.
Por exemplo,
\(\dfrac{2}{3}\)é simplificado porque não há fatores comuns de\(2\)\(3\) e.
\(\dfrac{10}{15}\)não é simplificado porque\(5\) é um fator comum de\(10\)\(15\) e.
Simplificamos ou reduzimos uma fração removendo os fatores comuns do numerador e do denominador. Uma fração não é simplificada até que todos os fatores comuns tenham sido removidos. Se uma expressão tiver frações, ela não será completamente simplificada até que as frações sejam simplificadas.
Às vezes, pode não ser fácil encontrar fatores comuns do numerador e do denominador. Quando isso acontece, uma boa ideia é fatorar o numerador e o denominador em números primos. Em seguida, divida os fatores comuns usando a propriedade de frações equivalentes.
Simplifique\(\dfrac{−315}{770}\).
- Resposta
-



Simplifique\(−\dfrac{69}{120}\).
- Resposta
-
\(−\dfrac{23}{40}\)
Simplifique\(−\dfrac{120}{192}\).
- Resposta
-
\(−\dfrac{5}{8}\)
Agora resumimos as etapas que você deve seguir para simplificar as frações.
- Reescreva o numerador e o denominador para mostrar os fatores comuns.
Se necessário, primeiro fatore o numerador e o denominador em números primos. - Simplifique o uso da propriedade de frações equivalentes dividindo os fatores comuns.
- Multiplique todos os fatores restantes.
Multiplique e divida frações
Muitas pessoas acham mais fácil multiplicar e dividir frações do que somar e subtrair frações.
Para multiplicar frações, multiplicamos os numeradores e multiplicamos os denominadores.
Se\(a\),\(b\)\(c\), e\(d\) são números onde\(b≠0\), e\(d≠0\), então
\[\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}\]
Para multiplicar frações, multiplique os numeradores e multiplique os denominadores.
Ao multiplicar frações, as propriedades dos números positivos e negativos ainda se aplicam, é claro. É uma boa ideia determinar o sinal do produto como primeira etapa. No exemplo, multiplicaremos o negativo e o positivo, então o produto será negativo.
Ao multiplicar uma fração por um número inteiro, pode ser útil escrever o inteiro como uma fração. Qualquer número inteiro, a, pode ser escrito como\(\dfrac{a}{1}\). Então, por exemplo,\(3=\dfrac{3}{1}\).
Multiplique:\(−\dfrac{12}{5}(−20x).\)
- Resposta
-
O primeiro passo é encontrar o sinal do produto. Como os sinais são os mesmos, o produto é positivo.
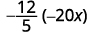
Determine o sinal do produto. Os sinais são os mesmos, então o produto é positivo.
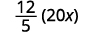
Escreva 20 x como uma fração. 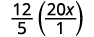
Multiplique. 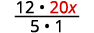
Reescreva 20 para mostrar o fator comum 5 e divida-o.
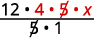
Simplifique. 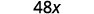
Multiplique:\(\dfrac{1}{13}(−9a)\).
- Resposta
-
\(−33a\)
Multiplique:\(\dfrac{13}{7}(−14b)\).
- Resposta
-
\(−26b\)
Agora que sabemos como multiplicar frações, estamos quase prontos para dividir. Antes de podermos fazer isso, precisamos de um pouco de vocabulário. O inverso de uma fração é encontrado invertendo a fração, colocando o numerador no denominador e o denominador no numerador. O recíproco de\(\frac{2}{3}\) é\(\frac{3}{2}\). Como 4 é escrito na forma fracionária como\(\frac{4}{1}\), o inverso de 4 é\(\frac{1}{4}\).
Para dividir frações, multiplicamos a primeira fração pelo inverso da segunda.
Se\(a\),\(b\)\(c\), e\(d\) são números onde\(b≠0\)\(c≠0\), e\(d≠0\), então
\[\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}⋅\frac{d}{c}\]
Para dividir frações, multiplicamos a primeira fração pelo inverso da segunda.
Precisamos dizer\(b≠0\), e\(c≠0\)\(d≠0\), para ter certeza de que não dividimos por zero!
Encontre o quociente:\(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)
- Resposta
-
\(−\dfrac{7}{18}÷(−\dfrac{14}{27})\) Para dividir, multiplique a primeira fração pelo inverso da segunda.
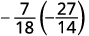
Determine o sinal do produto e multiplique.
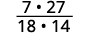
Reescreva mostrando fatores comuns. 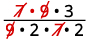
Remova os fatores comuns. 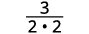
Simplifique. 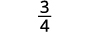
Divida:\(−\dfrac{7}{27}÷(−\dfrac{35}{36})\).
- Responda
-
\(\dfrac{4}{15}\)
Divida:\(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)
- Responda
-
\(\dfrac{2}{3}\)
Os numeradores ou denominadores de algumas frações contêm as próprias frações. Uma fração na qual o numerador ou o denominador é uma fração é chamada de fração complexa.
Uma fração complexa é uma fração na qual o numerador ou o denominador contém uma fração.
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]
Para simplificar uma fração complexa, lembre-se de que a barra de fração significa divisão. Por exemplo, a fração complexa\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) significa\(\dfrac{3}{4}÷\frac{5}{8}.\)
Simplifique:\(\dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}}\).
- Responda
-
\(\begin{array}{lc} \text{} & \dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}} \\[6pt] \text{Rewrite as division.} & \dfrac{x}{2}÷\dfrac{xy}{6} \\[6pt] \text{Multiply the first fraction by the reciprocal of the second.} & \dfrac{x}{2}·\dfrac{6}{xy} \\[6pt] \text{Multiply.} & \dfrac{x·6}{2·xy} \\[6pt] \text{Look for common factors.} & \dfrac{ \cancel{x}·3·\cancel{2}}{\cancel{2}·\cancel{x}·y} \\[6pt] \text{Divide common factors and simplify.} & \dfrac{3}{y} \end{array}\)
Simplifique:\(\dfrac{\dfrac{a}{8}}{ \dfrac{ab}{6}}\).
- Responda
-
\(\dfrac{3}{4b}\)
Simplifique:\(\dfrac{\dfrac{p}{2}}{ \dfrac{pq}{8}}\).
- Responda
-
\(\dfrac{4}{q}\)
Adicionar e subtrair frações
Quando multiplicamos frações, apenas multiplicamos os numeradores e multiplicamos os denominadores diretamente. Para somar ou subtrair frações, elas devem ter um denominador comum.
Se\(a\)\(b\), e\(c\) são números onde\(c≠0\), então
\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]
Para adicionar ou subtrair frações, adicione ou subtraia os numeradores e coloque o resultado sobre o denominador comum.
O denominador menos comum (LCD) de duas frações é o menor número que pode ser usado como denominador comum das frações. O LCD das duas frações é o mínimo múltiplo comum (LCM) de seus denominadores.
O menor denominador comum (LCD) de duas frações é o mínimo múltiplo comum (LCM) de seus denominadores.
Depois de encontrarmos o denominador menos comum de duas frações, convertemos as frações em frações equivalentes com o LCD. Juntar essas etapas nos permite somar e subtrair frações porque seus denominadores serão os mesmos!
Adicionar:\(\dfrac{7}{12}+\dfrac{5}{18}\).
- Responda
-



Adicionar:\(\dfrac{7}{12}+\dfrac{11}{15}\).
- Responda
-
\(\dfrac{79}{60}\)
Adicionar:\(\dfrac{13}{15}+\dfrac{17}{20}\).
- Responda
-
\(\dfrac{103}{60}\)
- Eles têm um denominador comum?
- Sim, vá para a etapa 2.
- Não — reescreva cada fração com o LCD (denominador menos comum).
- Encontre o LCD.
- Altere cada fração em uma fração equivalente com o LCD como seu denominador.
- Adicione ou subtraia as frações.
- Simplifique, se possível.
Agora temos todas as quatro operações para frações. A tabela resume as operações de frações.
| Multiplicação de frações | Divisão de frações |
|---|---|
| \(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\) | \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\) |
| Multiplique os numeradores e multiplique os denominadores | Multiplique a primeira fração pelo inverso da segunda. |
| Adição de frações | Subtração de frações |
| \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) | \(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\) |
| Adicione os numeradores e coloque a soma sobre o denominador comum. | Subtraia os numeradores e coloque a diferença sobre o denominador comum. |
|
Para multiplicar ou dividir frações, NÃO é necessário um LCD. Para adicionar ou subtrair frações, é necessário um LCD. |
|
Ao iniciar um exercício, sempre identifique a operação e, em seguida, lembre-se dos métodos necessários para essa operação.
Simplifique: ⓐ\(\dfrac{5x}{6}−\dfrac{3}{10}\) ⓑ\(\dfrac{5x}{6}·\dfrac{3}{10}\).
- Responda
-
Primeiro pergunte: “O que é a operação?” Identificar a operação determinará se precisamos ou não de um denominador comum. Lembre-se de que precisamos de um denominador comum para somar ou subtrair, mas não para multiplicar ou dividir.
ⓐ
\ (\ begin {array} {lc}\ text {O que é a operação? A operação é subtração.}\\ [6pt]\ text {As frações têm um denominador comum? Não.} &\ dfrac {5x} {6} −\ dfrac {3} {10}\\ [6pt]\ text {Encontre o LCD de} 6\ text {e} 10 &\ text {O LCD é 30.}\\ [6pt] {\ begin {align*} 6 & =2·3\\\ [6pt]
\;\;\ underline {\;\;\;\;\; 10\;\;\;\;} &\ sublinhado {=2·5\;\;\;\;}\;\ [6pt]
\ texto {LCD} & =2·3·5\\ [6 pt]
\ text {LCD} & =30\ end {align*}}\\ [6pt]\\\\
\ text {Reescreva cada fração como uma fração equivalente com o LCD.} &\ dfrac {5x·5} {6·5} −\ dfrac {3·3} {10·3}\\ [6pt]
\ text {} &\ dfrac {25x} {30} −\ dfrac {9} {30}\\ [6pt]
\ text {Subtraia os numeradores e coloque a diferença}\\ [6pt]
\ text {sobre o comum denominadores.} &\ dfrac {25x−9} {30}\\ [6pt]\\\
\ text {Simplifique, se possível.Não há fatores comuns.}\\ [6pt]
\ text {A fração é simplificada.} \ end {matriz}\)ⓑ
\(\begin{array}{lc} \text{What is the operation? Multiplication.} & \dfrac{25x}{6}·\dfrac{3}{10} \\ \text{To multiply fractions,multiply the numerators} \\ \text{and multiply the denominators.} & \dfrac{25x·3}{6·10} \\ \text{Rewrite, showing common factors.} \\ \text{Remove common factors.} & \dfrac{\cancel{5} x · \cancel{3}}{2·\cancel{3}·2·\cancel{5}} \\ \text{Simplify.} & \dfrac{x}{4} \end{array}\)
Observe que precisávamos de um LCD para adicionar\(\dfrac{25x}{6}−\dfrac{3}{10}\), mas não para multiplicar\(\dfrac{25x}{6}⋅\dfrac{3}{10}\).
Simplifique: ⓐ\(\dfrac{3a}{4}−\dfrac{8}{9}\) ⓑ\(\dfrac{3a}{4}·\dfrac{8}{9}\).
- Responda
-
ⓐ\(\dfrac{27a−32}{36}\) ⓑ\(\dfrac{2a}{3}\)
Simplifique: ⓐ\(\dfrac{4k}{5}−\dfrac{1}{6}\) ⓑ\(\dfrac{4k}{5}⋅\dfrac{1}{6}\).
- Responda
-
ⓐ\(\dfrac{24k−5}{30}\) ⓑ\(\dfrac{2k}{15}\)
Use a ordem das operações para simplificar as frações
A barra de fração em uma fração atua como símbolo de agrupamento. A ordem das operações então nos diz para simplificar o numerador e depois o denominador. Em seguida, dividimos.
- Simplifique a expressão no numerador. Simplifique a expressão no denominador.
- Simplifique a fração.
Para onde vai o sinal negativo em uma fração? Normalmente, o sinal negativo está na frente da fração, mas às vezes você verá uma fração com um numerador negativo ou às vezes com um denominador negativo. Lembre-se de que frações representam divisão. Quando o numerador e o denominador têm sinais diferentes, o quociente é negativo.
\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]
\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]
Para quaisquer números positivos\(a\) e\(b\),
\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]
Simplifique:\(\dfrac{4(−3)+6(−2)}{−3(2)−2}\).
- Responda
-
A barra de fração age como um símbolo de agrupamento. Portanto, simplifique completamente o numerador e o denominador separadamente.
\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)
Simplifique:\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\).
- Responda
-
4
Simplifique:\(\dfrac{7(−1)+9(−3)}{−5(3)−2}\).
- Responda
-
2
Agora, veremos frações complexas em que o numerador ou denominador contém uma expressão que pode ser simplificada. Portanto, primeiro devemos simplificar completamente o numerador e o denominador separadamente usando a ordem das operações. Em seguida, dividimos o numerador pelo denominador, pois a barra de fração significa divisão.
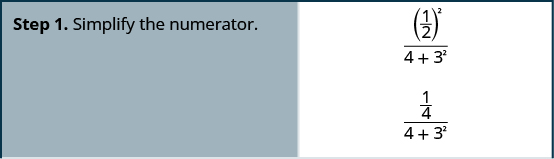
Simplifique:\(\dfrac{\left(\frac{1}{2}\right)^2}{4+3^2}\).
- Responda
-


Simplifique:\(\dfrac{\left(\frac{1}{3}\right)^2}{2^3+2}\).
- Responda
-
\(\frac{1}{90}\)
Simplifique:\(\dfrac{1+4^2}{\left(\frac{1}{4}\right)^2}\).
- Responda
-
272
- Simplifique o numerador.
- Simplifique o denominador.
- Divida o numerador pelo denominador. Simplifique, se possível.
Simplifique:\(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\).
- Responda
-
Pode ser útil colocar parênteses ao redor do numerador e do denominador.
\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)
Simplifique:\( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\).
- Responda
-
2
Simplifique:\(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\).
- Responda
-
\(\frac{2}{7}\)
Avalie expressões variáveis com frações
Já avaliamos expressões antes, mas agora podemos avaliar expressões com frações. Lembre-se de que, para avaliar uma expressão, substituímos o valor da variável na expressão e depois simplificamos.
Avalie\(2x^2y\) quando\(x=\frac{1}{4}\)\(y=−\frac{2}{3}\) e.
- Responda
-
Substitua os valores na expressão.
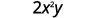
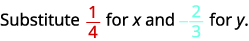
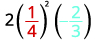
Simplifique primeiro os expoentes. 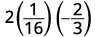
Multiplique; divida os fatores comuns. Observe que escrevemos 16 como 2⋅2⋅42·2·4 para facilitar a remoção de fatores comuns. 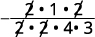
Simplifique. 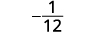
Avalie\(3ab^2\) quando\(a=−\frac{2}{3}\)\(b=−\frac{1}{2}\) e.
- Responda
-
\(−\dfrac{1}{2}\)
Avalie\(4c^3d\) quando\(c=−\frac{1}{2}\)\(d=−\frac{4}{3}\) e.
- Responda
-
\(\dfrac{2}{3}\)
Acesse este recurso on-line para obter instruções e práticas adicionais com frações.
- Adicionando frações com denominadores diferentes
Conceitos chave
- Se\(a\)\(b\), e\(c\) são números onde\(b≠0,c≠0\), então
\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)e\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
- Como simplificar uma fração.
- Reescreva o numerador e o denominador para mostrar os fatores comuns.
Se necessário, primeiro fatore o numerador e o denominador em números primos. - Simplifique o uso da propriedade de frações equivalentes dividindo os fatores comuns.
- Multiplique todos os fatores restantes.
- Reescreva o numerador e o denominador para mostrar os fatores comuns.
- Se\(a\),\(b\)\(c\), e\(d\) são números onde\(b≠0\), e\(d≠0\), então
\(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)
Para multiplicar frações, multiplique os numeradores e multiplique os denominadores.
- Se\(a\),\(b\)\(c\), e\(d\) são números onde\(b≠0\)\(c≠0\), e\(d≠0\), então
\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
Para dividir frações, multiplicamos a primeira fração pelo inverso da segunda.
- Se\(a\)\(b\), e\(c\) são números onde\(c≠0\), então
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
Para adicionar ou subtrair frações, adicione ou subtraia os numeradores e coloque o resultado sobre o denominador comum.
- Como adicionar ou subtrair frações.
- Eles têm um denominador comum?
- Sim, vá para a etapa 2.
- Não — reescreva cada fração com o LCD (denominador menos comum).
- Encontre o LCD.
- Altere cada fração em uma fração equivalente com o LCD como seu denominador.
- Adicione ou subtraia as frações.
- Simplifique, se possível.
- Eles têm um denominador comum?
- Como simplificar uma expressão com uma barra fracionária.
- Simplifique a expressão no numerador. Simplifique a expressão no denominador.
- Simplifique a fração.
- Para quaisquer números positivos\(a\) e\(b\),
\(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)
- Como simplificar frações complexas.
- Simplifique o numerador.
- Simplifique o denominador.
- Divida o numerador pelo denominador. Simplifique, se possível.
Glossário
- fração complexa
- Uma fração na qual o numerador ou o denominador é uma fração é chamada de fração complexa.
- denominador
- Em uma fração, escrita\(\dfrac{a}{b}\), onde\(b≠0\), o denominador\(b\) é o número de partes iguais em que o todo foi dividido.
- frações equivalentes
- Frações equivalentes são frações que têm o mesmo valor.
- fração
- Uma fração é escrita\(\dfrac{a}{b}\), onde\(b≠0\), e a é o numerador e\(b\) é o denominador. Uma fração representa partes de um todo.
- denominador menos comum
- O menor denominador comum (LCD) de duas frações é o mínimo múltiplo comum (LCM) de seus denominadores.
- numerador
- Em uma fração, escrita\(\dfrac{a}{b}\), onde\(b≠0\), o numerador a indica quantas partes estão incluídas.
- recíproca
- O inverso de uma fração é encontrado invertendo a fração, colocando o numerador no denominador e o denominador no numerador.


