15.6 : Oscillations amorties

Last updated
Save as PDF

Page ID: 191652

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Décrire le mouvement d'un mouvement harmonique amorti
Écrivez les équations du mouvement pour les oscillations harmoniques amorties
Décrire le mouvement d'un mouvement harmonique amorti, entraîné ou forcé
Écrivez les équations du mouvement pour un mouvement harmonique forcé et amorti

Dans le monde réel, les oscillations suivent rarement le vrai SHM. Une sorte de friction agit généralement pour amortir le mouvement afin qu'il disparaisse, ou qu'il nécessite plus de force pour continuer. Dans cette section, nous examinons quelques exemples de mouvement harmonique amorti et voyons comment modifier les équations du mouvement pour décrire ce cas plus général.

Une corde de guitare cesse d'osciller quelques secondes après avoir été pincée. Pour continuer à vous balancer sur une balançoire de terrain de jeu, vous devez continuer à pousser (Figure\(\PageIndex{1}\)). Bien que nous puissions souvent réduire ou minimiser les forces de friction et autres forces non conservatrices, les mouvements complètement non amortis sont rares. En fait, nous pouvons même vouloir amortir les oscillations, comme avec les amortisseurs de voiture.

Une photo d'une personne sur une balançoire — Figure\(\PageIndex{1}\) : Pour neutraliser les forces d'amortissement, vous devez continuer à pomper une balançoire. (crédit : Bob Mical)

La figure\(\PageIndex{2}\) montre une masse m attachée à un ressort avec une constante de force k. La masse est élevée jusqu'à une position A ₀, l'amplitude initiale, puis relâchée. La masse oscille autour de la position d'équilibre dans un fluide visqueux, mais l'amplitude diminue à chaque oscillation. Pour un système dont l'amortissement est faible, la période et la fréquence sont constantes et sont presque les mêmes que pour le SHM, mais l'amplitude diminue progressivement comme indiqué. Cela se produit parce que la force d'amortissement non conservatrice élimine l'énergie du système, généralement sous forme d'énergie thermique.

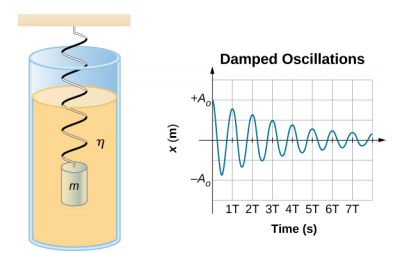
Une masse m est suspendue à un ressort vertical et immergée dans un fluide de viscosité eta. Un graphique de l'oscillation amortie montre le déplacement x en mètres sur l'axe vertical en fonction du temps en secondes sur l'axe horizontal. La plage de x va de moins A sous zéro à plus A sous zéro. L'échelle de temps va de zéro à 7 T, avec des tics par incréments de T. Le déplacement est plus A inférieur à zéro au temps zéro et oscille entre des maxima positifs et des minima négatifs, chaque cycle complet prenant le même temps T mais l'amplitude des oscillations diminuant avec le temps. — Figure\(\PageIndex{2}\) : Pour une masse sur un ressort oscillant dans un fluide visqueux, la période reste constante, mais les amplitudes des oscillations diminuent en raison de l'amortissement provoqué par le fluide.

Considérez les forces qui agissent sur la masse. Notez que la seule contribution du poids est de modifier la position d'équilibre, comme indiqué précédemment dans le chapitre. Par conséquent, la force nette est égale à la force du ressort et à la force d'amortissement (\(F_D\)). Si l'amplitude de la vitesse est faible, c'est-à-dire que la masse oscille lentement, la force d'amortissement est proportionnelle à la vitesse et agit à l'encontre du sens du mouvement (\(F_D = −b\)). La force nette sur la masse est donc

\[ma = -bv - kx \ldotp\]

En écrivant cela comme une équation différentielle en x, nous obtenons

\[m \frac{d^{2} x}{dt^{2}} + b \frac{dx}{dt} + kx = 0 \ldotp \label{15.23}\]

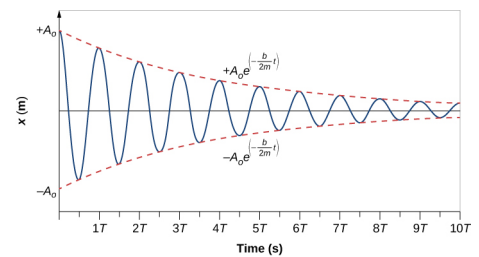
Pour déterminer la solution à cette équation, considérez le graphique de la position en fonction du temps illustré à la figure\(\PageIndex{3}\). La courbe ressemble à une courbe en cosinus oscillant dans l'enveloppe d'une fonction exponentielle\(A_0e^{−\alpha t}\) où\(\alpha = \frac{b}{2m}\). La solution est

\[x(t) = A_{0} e^{- \frac{b}{2m} t} \cos (\omega t + \phi) \ldotp \label{15.24}\]

Il s'agit d'un exercice visant à prouver que c'est effectivement la solution. Pour prouver que c'est la bonne solution, prenez les dérivées première et seconde par rapport au temps et remplacez-les dans l'équation 15.23. On constate que l'équation 15.24 est la solution si

\[\omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp\]

Rappelons que la fréquence angulaire d'une masse soumise à une SHM est égale à la racine carrée de la constante de force divisée par la masse. C'est ce que l'on appelle souvent la fréquence angulaire naturelle, qui est représentée par

\[\omega_{0} = \sqrt{\frac{k}{m}} \ldotp \label{15.25}\]

La fréquence angulaire du mouvement harmonique amorti devient

\[\omega = \sqrt{\omega_{0}^{2} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp \label{15.26}\]

La figure montre un graphique du déplacement, x en mètres, le long de l'axe vertical, en fonction du temps en secondes le long de l'axe horizontal. Le déplacement varie de moins A sous zéro à plus A sous zéro et le temps est compris entre 0 et 10 T. Le déplacement, représenté par une courbe bleue, oscille entre des maxima positifs et des minima négatifs, formant une onde dont l'amplitude diminue progressivement à mesure que l'on s'éloigne de t=0. Le temps, T, entre les crêtes adjacentes reste le même partout. L'enveloppe, la courbe lisse qui relie les crêtes et une autre courbe lisse qui relie les creux des oscillations, est représentée par deux lignes rouges pointillées. La courbe supérieure reliant les crêtes est étiquetée comme plus A sous zéro fois e à la quantité moins b t sur 2 m. La courbe inférieure reliant les creux est étiquetée comme moins A sous zéro fois e à la quantité moins b t sur 2 m. — Figure\(\PageIndex{3}\) : Position en fonction du temps de la masse oscillant sur un ressort dans un fluide visqueux. Notez que la courbe semble être une fonction cosinusoïdale à l'intérieur d'une enveloppe exponentielle.

Rappelons que lorsque nous avons commencé cette description du mouvement harmonique amorti, nous avons indiqué que l'amortissement devait être faible. Deux questions me viennent à l'esprit. Pourquoi l'amortissement doit-il être faible ? Et à quel point est petit ? Si vous augmentez progressivement le niveau d'amortissement d'un système, la période et la fréquence commencent à être affectées, car l'amortissement s'oppose et ralentit donc le mouvement de va-et-vient. (La force nette est plus faible dans les deux sens.) Si l'amortissement est très important, le système n'oscille même pas ; il se déplace lentement vers l'équilibre. La fréquence angulaire est égale à

\[\omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}} \ldotp\]

Lorsque b augmente,\(\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}\) devient plus petit et finit par atteindre zéro lorsque b =\(\sqrt{4mk}\). Si b devient plus grand,\(\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}\) devient un nombre négatif et\(\sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}}\) est un nombre complexe.

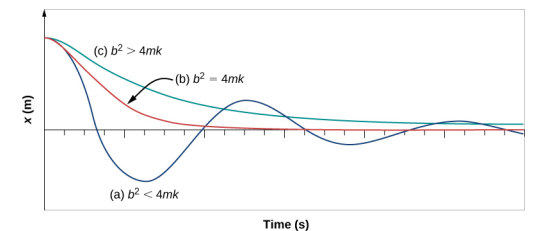
Position, x en mètres sur l'axe vertical, par rapport au temps en secondes sur l'axe horizontal, avec différents degrés d'amortissement. Aucune échelle n'est donnée pour l'un ou l'autre axe. Les trois courbes commencent à la même position positive au temps zéro. La courbe bleue a, marquée par b au carré, est inférieure à 4 m k, subit un peu plus de deux oscillations et quart d'amplitude décroissante et de période constante. La courbe rouge b, repérée par b au carré est égale à 4 m k, décroît à t=0 moins rapidement que la courbe bleue, mais n'oscille pas. La courbe rouge s'approche de x=0 de façon asymptotique et est presque nulle à moins d'une oscillation de la courbe bleue. La courbe verte c, marquée par b au carré, est supérieure à 4 m k, diminue à t=0 moins rapidement que la courbe rouge et n'oscille pas. La courbe verte se rapproche de x=0 de façon asymptotique, mais elle se situe toujours nettement au-dessus de zéro à la fin du graphique, après plus de deux oscillations de la courbe bleue. — Figure\(\PageIndex{4}\) : La position en fonction du temps pour trois systèmes composés d'une masse et d'un ressort dans un fluide visqueux. (a) Si l'amortissement est faible (b <\(\sqrt{4mk}\)), la masse oscille et perd lentement de l'amplitude à mesure que l'énergie est dissipée par la ou les forces non conservatrices. Le cas limite est (b) où l'amortissement est (b =\(\sqrt{4mk}\)). (c) Si l'amortissement est très important (b >\(\sqrt{4mk}\)), la masse n'oscille pas lorsqu'elle est déplacée, mais tente de revenir à la position d'équilibre.

La figure\(\PageIndex{4}\) montre le déplacement d'un oscillateur harmonique pour différents niveaux d'amortissement.

Lorsque la constante d'amortissement est faible, b <\(\sqrt{4mk}\), le système oscille tandis que l'amplitude du mouvement diminue de façon exponentielle. Ce système est dit sous-amorti, comme dans la courbe (a). De nombreux systèmes sont sous-amortis et oscillent alors que l'amplitude diminue de façon exponentielle, comme la masse oscillant sur un ressort. L'amortissement peut être assez faible, mais la masse finit par s'immobiliser.
Si la constante d'amortissement est égale à\(b = \sqrt{4mk}\), le système est considéré comme étant soumis à un amortissement critique, comme dans la courbe (\(b\)). Les amortisseurs d'une voiture sont un exemple de système à amortissement critique. Il est avantageux que les oscillations diminuent le plus rapidement possible. Ici, le système n'oscille pas, mais s'approche de manière asymptotique de la condition d'équilibre le plus rapidement possible.
La courbe (c) de la figure\(\PageIndex{4}\) représente un système suramorti où\(b > \sqrt{4mk}\). Un système suramorti atteindra l'équilibre sur une plus longue période.

Un amortissement critique est souvent souhaité, car un tel système revient rapidement à l'équilibre et le reste également. De plus, une force constante appliquée à un système à amortissement critique déplace le système vers une nouvelle position d'équilibre dans les plus brefs délais sans dépasser ou osciller autour de la nouvelle position.

Exercice\(\PageIndex{1}\)

Pourquoi les oscillateurs harmoniques totalement non amortis sont-ils si rares ?