15.5 : Pendules

Last updated
Save as PDF

Page ID: 191620

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Indiquez les forces qui agissent sur un simple pendule
Déterminer la fréquence angulaire, la fréquence et la période d'un pendule simple en termes de longueur du pendule et d'accélération due à la gravité
Définir la période d'un pendule physique
Définir la période d'un pendule de torsion

Les pendules sont d'usage courant. Les horloges Grandfather utilisent un pendule pour indiquer l'heure et un pendule peut être utilisé pour mesurer l'accélération due à la gravité. Pour les petits déplacements, un pendule est un simple oscillateur harmonique.

Le pendule simple

Un pendule simple est défini comme ayant une masse ponctuelle, également appelée bob du pendule, qui est suspendue à une chaîne de longueur L avec une masse négligeable (Figure$\PageIndex{1}$). Ici, les seules forces qui agissent sur le bob sont la force de gravité (c'est-à-dire le poids du bob) et la tension exercée par la corde. La masse de la corde est supposée être négligeable par rapport à la masse du bob.

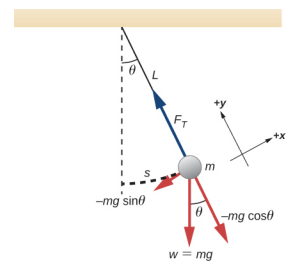
Sur la figure, une barre horizontale est représentée. Une chaîne de longueur L s'étend depuis la barre selon un angle thêta dans le sens antihoraire par rapport à la verticale. La direction verticale est indiquée par une ligne pointillée s'étendant vers le bas à partir de l'endroit où la ficelle est attachée à la barre. Un fil circulaire de masse m est fixé à l'extrémité inférieure de la corde. L'arc allant de la masse à la verticale est indiqué par une autre ligne pointillée et a une longueur s. Une flèche rouge indiquant le temps T de l'oscillation de la foule est indiquée le long de la ligne de corde vers la barre. Un système de coordonnées est affiché près du bob, la direction y positive étant alignée avec la chaîne et pointant vers le point de pivot et la direction x positive pointant tangente à l'arc et s'éloignant de la position d'équilibre. Une flèche bleue allant du bob vers le pivot, le long de la chaîne, est étiquetée F sub T. Une flèche rouge partant du bob pointant vers le bas est étiquetée w = m g. Une flèche rouge pointant tangente à l'arc et vers l'équilibre, dans la direction moins x, est étiquetée moins m g sinus thêta. Une flèche rouge faisant un angle thêta dans le sens antihoraire par rapport à w est étiquetée moins m g cosinus thêta. — Figure$\PageIndex{1}$ : Un pendule simple possède un bob de petit diamètre et une ficelle de très faible masse mais suffisamment solide pour ne pas s'étirer de façon appréciable. Le déplacement linéaire par rapport à l'équilibre est s, la longueur de l'arc. Les forces sur le bob sont également affichées, qui se traduisent par une force nette de −mgsin$\theta$ vers la position d'équilibre, c'est-à-dire une force de rappel.

Tenez compte du couple sur le pendule. La force fournissant le couple de rappel est la composante du poids du balancier qui agit le long de la longueur de l'arc. Le couple est la longueur de la corde L multipliée par la composante de la force nette qui est perpendiculaire au rayon de l'arc. Le signe moins indique que le couple agit dans la direction opposée au déplacement angulaire :

\[\begin{split} \tau & = -L (mg \sin \theta); \\ I \alpha & = -L (mg \sin \theta); \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ mL^{2} \frac{d^{2} \theta}{dt^{2}} & = -L (mg \sin \theta); \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{g}{L} \sin \theta \ldotp \end{split}\]

La solution à cette équation différentielle implique un calcul avancé et dépasse le cadre de ce texte. Mais notez que pour les petits angles (inférieurs à 15°), sin$\theta$ et$\theta$ différent de moins de 1 %, nous pouvons donc utiliser l'approximation du petit angle sin$\theta$ ≈$\theta$. L'angle$\theta$ décrit la position du pendule. L'utilisation de l'approximation des petits angles donne une solution approximative pour les petits angles,

\[\frac{d^{2} \theta}{dt^{2}} = - \frac{g}{L} \theta \ldotp \label{15.17}\]

Comme cette équation a la même forme que l'équation de SHM, la solution est facile à trouver. La fréquence angulaire est

\[\omega = \sqrt{\frac{g}{L}} \label{15.18}\]

et la période est

\[T = 2 \pi \sqrt{\frac{L}{g}} \ldotp \label{15.19}\]

La période d'un pendule simple dépend de sa longueur et de l'accélération due à la gravité. La période est totalement indépendante d'autres facteurs, tels que la masse et le déplacement maximal. Comme pour les oscillateurs harmoniques simples, la période T d'un pendule est presque indépendante de l'amplitude, surtout si elle$\theta$ est inférieure à environ 15°. Même les horloges pendulaires simples peuvent être ajustées avec précision et rester précises.

Notez la dépendance de T par rapport à g. Si la longueur d'un pendule est connue avec précision, elle peut effectivement être utilisée pour mesurer l'accélération due à la gravité, comme dans l'exemple suivant.

Exemple$\PageIndex{1}$: Measuring Acceleration due to Gravity by the Period of a Pendulum

Quelle est l'accélération due à la gravité dans une région où un simple pendule d'une longueur de 75 000 cm a une période de 1,7357 s ?

Stratégie

On nous demande de trouver g en fonction de la période T et de la longueur L d'un pendule. On peut résoudre T = 2$\pi$ L g pour g, en supposant seulement que l'angle de déflexion est inférieur à 15°.

Solution

Carré T = 2$\pi \sqrt{\frac{L}{g}}$ et résolvez pour g : $$g = 4 \ pi^ {2} \ frac {L} {T^ {2}} ldotp$$
Substituez des valeurs connues dans la nouvelle équation : $$g = 4 \ pi^ {2} \ frac {0,75000 \ ; m} {(1,7357 \ ; s) ^ {2}} \ ldotp$$
Calculez pour trouver g : $$g = 9,8281 \ ; m/s^ {2} \ ldotp$$

L'importance

Cette méthode de détermination de g peut être très précise, c'est pourquoi la longueur et la période sont données à cinq chiffres dans cet exemple. Pour que la précision de l'approximation sin$\theta$ ≈$\theta$ soit meilleure que la précision de la longueur et de la période du pendule, l'angle de déplacement maximal doit être maintenu en dessous d'environ 0,5°.

Exercice$\PageIndex{1}$

Un ingénieur construit deux pendules simples. Les deux sont suspendus à de petits fils fixés au plafond d'une pièce. Chaque pendule plane à 2 cm au-dessus du sol. Le pendule 1 a un bob d'une masse de 10 kg. Le pendule 2 a un bob d'une masse de 100 kg. Décrivez en quoi le mouvement des pendules sera différent si les bobs sont tous deux déplacés de 12°.

Pendule physique

Tout objet peut osciller comme un pendule. Prenons l'exemple d'une tasse à café accrochée à un crochet dans le garde-manger. Si le mug est renversé, il oscille d'avant en arrière comme un pendule jusqu'à ce que les oscillations s'éteignent. Nous avons décrit un pendule simple comme une masse ponctuelle et une corde. Un pendule physique est un objet dont les oscillations sont similaires à celles du pendule simple, mais ne peuvent pas être modélisés comme une masse ponctuelle sur une corde, et la distribution des masses doit être incluse dans l'équation du mouvement.

En ce qui concerne le pendule simple, la force de rappel du pendule physique est la force de gravité. Avec le pendule simple, la force de gravité agit sur le centre du balancier. Dans le cas du pendule physique, la force de gravité agit sur le centre de gravité (CM) d'un objet. L'objet oscille autour d'un point O. Prenons l'exemple d'un objet de forme générique, comme illustré à la figure$\PageIndex{2}$.

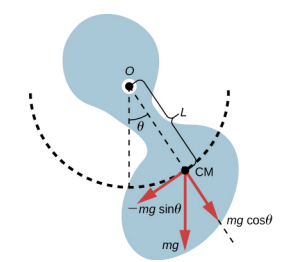
Dessin d'un pendule physique. Sur la figure, le pendule est un objet de forme irrégulière. Le centre de gravité, C M, se trouve à une distance L du point de pivot, O. Le centre de masse trace un arc de cercle centré sur O. La ligne allant de O à L forme un angle thêta dans le sens antihoraire par rapport à la verticale. Trois forces sont représentées par des flèches rouges au centre de gravité. La force m g pointe vers le bas. Ses composantes sont moins m g sinusoïdal thêta qui pointe tangent à l'arc tracé par le centre de masse, et m g cosinus thêta qui pointe radialement vers l'extérieur. — Figure$\PageIndex{2}$ : Un pendule physique est un objet qui oscille comme un pendule, mais qui ne peut pas être modélisé comme une masse ponctuelle sur une corde. La force de gravité agit sur le centre de gravité (CM) et fournit la force de rappel qui fait osciller l'objet. Le signe moins sur la composante du poids qui fournit la force de rappel est présent parce que la force agit dans la direction opposée à l'angle croissant$\theta$.

Lorsqu'un pendule physique est suspendu à un point mais qu'il est libre de tourner, il tourne en raison du couple appliqué au CM, produit par la composante du poids de l'objet qui agit de manière tangente au mouvement du CM. Si l'on considère que le sens antihoraire est positif, la composante de la force gravitationnelle qui agit tangentiellement au mouvement est −mg sin$\theta$. Le signe moins est le résultat de la force de rappel agissant dans la direction opposée à l'angle croissant. Rappelez-vous que le couple est égal à$\vec{\tau} = \vec{r} \times \vec{F}$. L'amplitude du couple est égale à la longueur du bras radial multipliée par la composante tangentielle de la force appliquée, |$\tau$ | = RFSin$\theta$. Ici, la longueur L du bras radial est la distance entre le point de rotation et le CM. Pour analyser le mouvement, commencez par le couple net. Comme pour le pendule simple, ne considérez que de petits angles pour que sin$\theta$ ≈$\theta$. Rappelons, d'après Rotation à axe fixe lors de la rotation, que le couple net est égal au moment d'inertie I =$\int$ r ² dm fois l'accélération angulaire$\alpha$, où \ (\ alpha = \ frac {d^ {2} \ theta} {dt^ {2}} :

\[I \alpha = \tau_{net} = L (-mg) \sin \theta \ldotp\]

Utilisation de l'approximation du petit angle et réorganisation :

\[\begin{split} I \alpha & = -L (mg) \theta; \\ I \frac{d^{2} \theta}{dt^{2}} & = -L (mg) \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \left(\dfrac{mgL}{I}\right) \theta \ldotp \end{split}\]

Encore une fois, l'équation indique que la dérivée temporelle seconde de la position (dans ce cas, l'angle) est égale à moins une constante$\left(− \dfrac{mgL}{I}\right)$ multipliée par la position. La solution est

\[\theta (t) = \Theta \cos (\omega t + \phi),\]

où$\Theta$ est le déplacement angulaire maximal. La fréquence angulaire est

\[\omega = \sqrt{\frac{mgL}{I}} \ldotp \label{15.20}\]

La période est donc

\[T = 2 \pi \sqrt{\frac{I}{mgL}} \ldotp \label{15.21}\]

Notez que pour un pendule simple, le moment d'inertie est I =$\int$ r ² dm = mL ² et la période se réduit à T = 2$\pi \sqrt{\frac{L}{g}}$.

Exemple$\PageIndex{2}$: Reducing the Swaying of a Skyscraper

Dans des conditions extrêmes, les gratte-ciel peuvent osciller jusqu'à deux mètres avec une fréquence allant jusqu'à 20,00 Hz en raison de vents violents ou d'une activité sismique. Plusieurs entreprises ont développé des pendules physiques qui sont placés au sommet des gratte-ciel. Lorsque le gratte-ciel se balance vers la droite, le pendule oscille vers la gauche, réduisant ainsi le balancement. En supposant que les oscillations ont une fréquence de 0,50 Hz, concevez un pendule composé d'un long faisceau, de densité constante, d'une masse de 100 tonnes métriques et d'un point de pivot à une extrémité du faisceau. Quelle doit être la longueur du faisceau ?

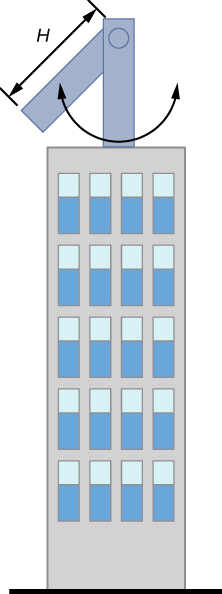
La figure représente un grand bâtiment avec une colonne sur son toit et une longue tige de longueur H qui pivote sur un point de pivot situé près du sommet de la colonne.

Stratégie

On nous demande de déterminer la longueur du pendule physique avec une masse connue. Il faut d'abord déterminer le moment d'inertie du faisceau. Nous pouvons ensuite utiliser l'équation de la période d'un pendule physique pour déterminer la longueur.

Solution

Détermine le moment d'inertie du CM.
Utilisez le théorème de l'axe parallèle pour déterminer le moment d'inertie autour du point de rotation : $$I = I_ {CM} + \ frac {L^ {2}} {4} M = \ frac {1} {12} ML^ {2} + \ frac {1} {4} ML^ {2} = \ frac {1} {3} ML^ {2} \ ldotp$$
La période d'un pendule physique a une période de T = 2$\pi \sqrt{\frac{I}{mgL}}$. Utilisez le moment d'inertie pour obtenir la longueur L : $$ \ begin {split} T & = 2 \ pi \ sqrt {\ frac {I} {mgL}} = 2 \ pi \ sqrt {\ frac {\ frac {1} {3} ML^ {2}} {mGL}} = 2 \ pi \ sqrt {\ frac {L} {3g}} ; \ L & = 3g \ left (\ dfrac {T} {2 \ pi} \ right) ^ {2} = 3 (9,8 \ ; m/s^ {2}) \ left (\ dfrac {2 \ ; s} {2 \ pi} \ right) ^ {2} = 2,98 \ ; m \ ldotp \ end { divisé} $$
Cette longueur L va du centre de gravité à l'axe de rotation, qui est la moitié de la longueur du pendule. La longueur H du pendule est donc : $$ H = 2L = 5,96 \ : m $$

L'importance

Il existe de nombreuses façons de réduire les oscillations, notamment en modifiant la forme des gratte-ciel, en utilisant plusieurs pendules physiques et en utilisant des amortisseurs à masse réglée.

Pendule de torsion

Un pendule de torsion est constitué d'un corps rigide suspendu par un fil léger ou un ressort (Figure$\PageIndex{3}$). Lorsque le corps est tordu d'un petit angle maximum ($\Theta$) et qu'il est libéré du repos, le corps oscille entre ($\theta$= +$\Theta$) et ($\theta$= −$\Theta$). Le couple de rappel est fourni par le cisaillement du fil ou du fil.

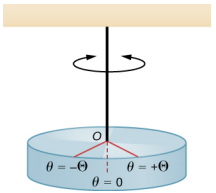
Le couple de rappel peut être modélisé comme étant proportionnel à l'angle :

\[\tau = - \kappa \theta \ldotp\]

La variable kappa ($\kappa$) est connue sous le nom de constante de torsion du fil ou de la corde. Le signe moins indique que le couple de rappel agit dans la direction opposée à l'augmentation du déplacement angulaire. Le couple net est égal au moment d'inertie multiplié par l'accélération angulaire :

\[\begin{split} I \frac{d^{2} \theta}{dt^{2}} & = - \kappa \theta; \\ \frac{d^{2} \theta}{dt^{2}} & = - \frac{\kappa}{I} \theta \ldotp \end{split}\]

Cette équation indique que la dérivée temporelle seconde de la position (dans ce cas, l'angle) est égale à une constante négative multipliée par la position. Cela ressemble beaucoup à l'équation du mouvement pour le SHM$\frac{d^{2} x}{dt^{2}}$ = −$\frac{k}{m}$ x, où la période a été trouvée comme étant T = 2$\pi \sqrt{\frac{m}{k}}$. Par conséquent, la période du pendule de torsion peut être déterminée en utilisant

\[T = 2 \pi \sqrt{\frac{I}{\kappa}} \ldotp \label{15.22}\]

Les unités de la constante de torsion sont [$\kappa$] = N • m = (kg • m/s ²) m = kg • m ² /s ² et les unités du moment d'inertie sont [I] = kg • m ², ce qui indique que l'unité de la période est la seconde.

Exemple$\PageIndex{3}$: Measuring the Torsion Constant of a String

Une tige a une longueur de l = 0,30 m et une masse de 4,00 kg. Une ficelle est fixée au CM de la tige et le système est suspendu au plafond (Figure$\PageIndex{4}$). La tige est déplacée de 10° par rapport à la position d'équilibre et libérée du repos. La tige oscille pendant 0,5 s. Quelle est la constante de torsion$\kappa$ ?

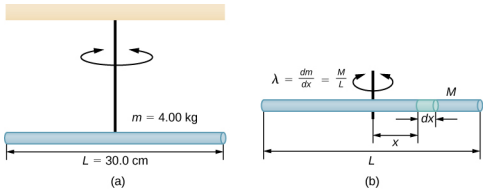
La figure a montre une tige horizontale, d'une longueur de 30,0 centimètres et d'un poids de 4,00 kilogrammes, suspendue par une ficelle au plafond. La ficelle se fixe au milieu de la tige. La tige tourne avec la ficelle dans le plan horizontal. La figure b montre la tige avec les détails nécessaires pour déterminer son moment d'inertie. La longueur de la tige, bout à bout, est L et sa masse totale est M. Elle a une densité massique linéaire lambda égale à d m d x qui est également égale à M sur L. Un petit segment de la tige qui a une longueur d x à une distance x du centre de la tige est surligné. La ficelle est fixée à la tige au centre de la tige. — Figure$\PageIndex{4}$ - (a) Une tringle suspendue par une ficelle au plafond. (b) Déterminer le moment d'inertie de la tige.

Stratégie

On nous demande de trouver la constante de torsion de la corde. Il faut d'abord trouver le moment d'inertie.

Solution

Trouvez le moment d'inertie du CM : $$I_ {CM} = \ int x^ {2} dm = \ int_ {- \ frac {L} {2}} ^ {+ \ frac {L} {2}} x^ {2}} \ lambda dx = \ lambda \ Bigg [\ frac {x^ {3}} {3} \ Bigg] _ {- frac {x^ {3}} \ Bigg] _ {- frac {x^ {3}} \ Bigg] _ {- frac {x^ {3}} \ Bigg] _ {- ac {L} {2}} ^ {+ \ frac {L} {2}} = \ lambda \ frac {2L^ {3}} {24} = \ gauche (\ dfrac {M} {L} \ droite) \ frac {2L^ {3}} {24} = \ frac {1} {12} ML^ {2} \ ldotp$$
Calculez la constante de torsion à l'aide de l'équation pour la période : $$ \ begin {split} T & = 2 \ pi \ sqrt {\ frac {I} {\ kappa}} ; \ \ \ kappa & = I \ left (\ dfrac {2 \ pi} {T} \ right) ^ {2} = \ left (\ dfrac {1} {12} ML^ {2} \ right) \ left (\ dfrac {2 \ pi} {T} \ right) ^ {2} ; \ \ & = \ Grand [\ frac {1} {12} (4,00 \ ; kg) (0,30 \ ; m) ^ {2} \ Grand] \ left (\ dfrac {2 \ pi} {0,50 \ ; s} \ right) ^ {2} = 4,73 \ ; N \ ; \ cdotp m \ ldotp \ end {split} $$

L'importance

Comme la constante de force du système composé d'un bloc et d'un ressort, plus la constante de torsion est grande, plus la période est courte.

Exemple\(\PageIndex{1}\): Measuring Acceleration due to Gravity by the Period of a Pendulum

Solution

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Reducing the Swaying of a Skyscraper

Solution

Exemple\(\PageIndex{3}\): Measuring the Torsion Constant of a String

Solution