15.7 : Oscillations forcées

Objectifs d'apprentissage

• Définir les oscillations forcées
• Répertorier les équations de mouvement associées aux oscillations forcées
• Expliquer le concept de résonance et son impact sur l'amplitude d'un oscillateur
• Énumérer les caractéristiques d'un système oscillant en résonance

Asseyez-vous un jour devant un piano et chantez-y une brève note forte, les amortisseurs n'étant pas attachés à ses cordes (Figure\(\PageIndex{1}\)). Il vous chantera la même note : les cordes, ayant les mêmes fréquences que votre voix, résonnent en réponse aux forces des ondes sonores que vous leur avez envoyées. C'est un bon exemple du fait que les objets, en l'occurrence les cordes de piano, peuvent être forcés à osciller et oscillent le plus facilement à leur fréquence naturelle. Dans cette section, nous explorons brièvement l'application d'une force motrice périodique agissant sur un oscillateur harmonique simple. La force motrice injecte de l'énergie dans le système à une certaine fréquence, qui n'est pas nécessairement la même que la fréquence naturelle du système. Rappelons que la fréquence naturelle est la fréquence à laquelle un système oscillerait en l'absence de force motrice et d'amortissement.

Figure\(\PageIndex{1}\) : - Vous pouvez faire vibrer les cordes d'un piano simplement en produisant des ondes sonores à partir de votre voix.

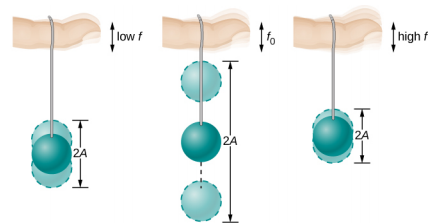
La plupart d'entre nous ont joué avec des jouets impliquant un objet soutenu par un élastique, un peu comme la balle à pagaie suspendue à un doigt dans Figure\(\PageIndex{2}\). Imaginez que le doigt sur la figure est votre doigt. Au début, vous maintenez votre doigt fermement et la balle rebondit de haut en bas avec un léger amortissement. Si vous déplacez lentement votre doigt de haut en bas, la balle suit sans trop rebondir d'elle-même. Lorsque vous augmentez la fréquence à laquelle vous déplacez votre doigt de haut en bas, la balle répond en oscillant avec une amplitude croissante. Lorsque vous lancez la balle à sa fréquence naturelle, les oscillations de la balle augmentent en amplitude à chaque oscillation aussi longtemps que vous la conduisez. Le phénomène consistant à piloter un système avec une fréquence égale à sa fréquence naturelle est appelé résonance. On dit qu'un système entraîné à sa fréquence naturelle résonne. À mesure que la fréquence d'entraînement augmente progressivement par rapport à la fréquence de résonance ou naturelle, l'amplitude des oscillations diminue jusqu'à ce que les oscillations disparaissent presque, et votre doigt se déplace simplement de haut en bas avec peu d'effet sur la balle.

Figure\(\PageIndex{2}\) : La balle à pagaie sur son élastique se déplace en réponse au doigt qui la soutient. Si le doigt se déplace avec la fréquence naturelle f0 de la balle sur l'élastique, une résonance est obtenue et l'amplitude des oscillations de la balle augmente considérablement. À des fréquences de conduite plus élevées et plus basses, l'énergie est transférée à la balle de manière moins efficace et celle-ci répond par des oscillations de plus faible amplitude.

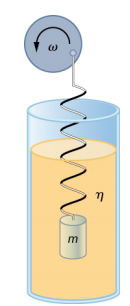
Envisagez une expérience simple. Attachez une masse m à un ressort dans un fluide visqueux, de la même manière que l'appareil décrit dans l'oscillateur harmonique amorti. Cette fois, au lieu de fixer l'extrémité libre du ressort, fixez l'extrémité libre à un disque entraîné par un moteur à vitesse variable. Le moteur tourne avec une fréquence angulaire d'entraînement de ω. Le disque rotatif fournit de l'énergie au système grâce au travail effectué par la force motrice (F _d = F ₀ sin (\(\omega\)t)). L'appareil expérimental est illustré sur la figure\(\PageIndex{3}\).

Figure\(\PageIndex{3}\) : Mouvement harmonique forcé et amorti produit par l'entraînement d'un ressort et d'une masse à l'aide d'un disque entraîné par un moteur à vitesse variable.

En utilisant la deuxième loi de Newton (\(\vec{F}_{net} = m \vec{a}\)), nous pouvons analyser le mouvement de la masse. L'équation résultante est similaire à l'équation de force pour l'oscillateur harmonique amorti, avec l'ajout de la force motrice :

\[-kx -b \frac{dx}{dt} + F_{0} \sin (\omega t) = m \frac{d^{2} x}{dt^{2}} \ldotp \label{15.27}\]

Lorsqu'un oscillateur est forcé par une force motrice périodique, le mouvement peut sembler chaotique. Les mouvements de l'oscillateur sont appelés transitoires. Une fois les transitoires éteints, l'oscillateur atteint un état stable, où le mouvement est périodique. Après un certain temps, la solution en régime permanent de cette équation différentielle est

\[x(t) = A \cos (\omega t + \phi) \ldotp \label{15.28}\]

Encore une fois, il s'agit d'un exercice pour prouver que cette équation est une solution. Le fait de prendre les dérivées temporelles première et seconde de x (t) et de les substituer dans l'équation de force montre que x (t\(\omega t + \phi\)) = Asin () est une solution tant que l'amplitude est égale à

\[A = \frac{F_{0}}{\sqrt{m^{2} (\omega^{2} - \omega_{0}^{2})^{2} + b^{2} \omega^{2}}} \label{15.29}\]

où\(\omega_{0} = \sqrt{\frac{k}{m}}\) est la fréquence angulaire naturelle du système de la masse et du ressort. Rappelons que la fréquence angulaire, et donc la fréquence, du moteur peuvent être ajustées. Si l'on considère le dénominateur de l'équation de l'amplitude, lorsque la fréquence motrice est beaucoup plus petite ou beaucoup plus grande que la fréquence naturelle, le carré de la différence entre les deux fréquences angulaires\((\omega^{2} − \omega_{0}^{2})^{2}\) est positif et grand, ce qui rend le dénominateur grand, et le résultat est une faible amplitude pour les oscillations de la masse. Lorsque la fréquence de la force motrice se rapproche de la fréquence naturelle du système, le dénominateur devient petit et l'amplitude des oscillations devient grande. L'amplitude maximale est obtenue lorsque la fréquence de la force motrice est égale à la fréquence naturelle du système (A _max =\(\frac{F_{0}}{b \omega}\)).

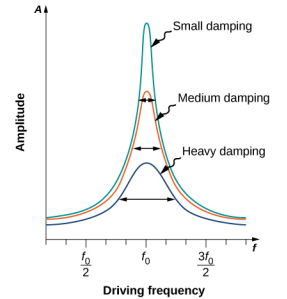
La figure\(\PageIndex{4}\) montre un graphique de l'amplitude d'un oscillateur harmonique amorti en fonction de la fréquence de la force périodique qui l'entraîne. Chacune des trois courbes du graphique représente un niveau d'amortissement différent. Les trois courbes culminent au point où la fréquence de la force motrice est égale à la fréquence naturelle de l'oscillateur harmonique. Le pic le plus élevé, ou réponse la plus élevée, correspond à l'amortissement le moins important, car moins d'énergie est retirée par la force d'amortissement. Notez que puisque l'amplitude augmente à mesure que l'amortissement diminue, jusqu'à la limite où il n'y a pas d'amortissement (b = 0), l'amplitude devient infinie.

Notez qu'une force motrice de faible amplitude peut produire une réponse de grande amplitude. Ce phénomène est connu sous le nom de résonance. Un exemple courant de résonance est celui d'un parent qui pousse un petit enfant sur une balançoire. Lorsque l'enfant veut monter plus haut, le parent ne recule pas, puis, prenant un bon départ, percute l'enfant en appliquant une force importante dans un court intervalle. Au lieu de cela, le parent applique de petites pressions à l'enfant à la bonne fréquence, et l'amplitude des balançoires de l'enfant augmente.

Figure\(\PageIndex{4}\) : Amplitude d'un oscillateur harmonique en fonction de la fréquence de la force motrice. Les courbes représentent le même oscillateur avec la même fréquence naturelle mais avec des niveaux d'amortissement différents. La résonance se produit lorsque la fréquence de conduite est égale à la fréquence naturelle et que la réponse la plus élevée est celle qui consiste à amortir le moins possible. La réponse la plus étroite est également celle qui permet le moins d'amortissement.

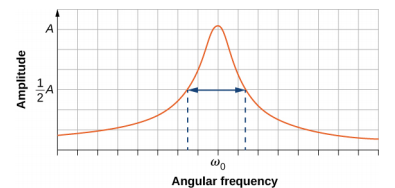
Il est intéressant de noter que les largeurs des courbes de résonance illustrées sur la figure\(\PageIndex{4}\) dépendent de l'amortissement : moins l'amortissement est faible, plus la résonance est étroite. La conséquence est que si vous voulez qu'un oscillateur entraîné résonne à une fréquence très spécifique, vous avez besoin d'un amortissement aussi faible que possible. Par exemple, une radio possède un circuit qui permet de choisir une station de radio particulière. Dans ce cas, l'oscillateur à amortissement forcé se compose d'une résistance, d'un condensateur et d'une inductance, dont il sera question plus loin dans ce cours. Le circuit est « réglé » pour sélectionner une station de radio en particulier. Ici, il est souhaitable que la courbe de résonance soit très étroite, afin de déterminer la fréquence exacte de la station radio choisie. L'étroitesse du graphique et la possibilité de sélectionner une certaine fréquence sont connues sous le nom de qualité du système. La qualité est définie comme l'étalement de la fréquence angulaire ou, de manière équivalente, l'étalement de la fréquence, à la moitié de l'amplitude maximale, divisé par la fréquence naturelle (Q =\(\frac{\Delta \omega}{\omega_{0}}\)), comme indiqué sur la figure\(\PageIndex{5}\). Pour un faible amortissement, la qualité est approximativement égale à Q ≈\(\frac{2b}{m}\).

Figure\(\PageIndex{5}\) : La qualité d'un système est définie comme la répartition des fréquences à la moitié de l'amplitude divisée par la fréquence naturelle.

Ces caractéristiques des oscillateurs harmoniques entraînés s'appliquent à une grande variété de systèmes. Par exemple, l'imagerie par résonance magnétique (IRM) est un outil de diagnostic médical largement utilisé dans lequel les noyaux atomiques (principalement des noyaux d'hydrogène ou des protons) sont amenés à résonner par les ondes radio entrantes (de l'ordre de 100 MHz). Dans tous ces cas, l'efficacité du transfert d'énergie de la force motrice vers l'oscillateur est optimale lors de la résonance. La figure\(\PageIndex{6}\) montre la passerelle London Millennium qui permet aux piétons de traverser la Tamise à Londres. Ce pont a été surnommé « Wobbly Bridge » lorsque les piétons se balançaient lorsqu'ils le traversaient. Le pont a été fermé pendant environ deux ans afin de mettre fin à ce mouvement.

Figure\(\PageIndex{6}\) : Au début, lorsque les gens ont traversé la passerelle du Millennium de Londres, ils ont ressenti un mouvement de balancement. Les personnes qui continuaient à traverser ont renforcé l'amplitude de l'oscillation, augmentant ainsi le balancement problématique. (crédit : Adrian Pingstone/Wikimedia Commons)

Exercice 15.6

Un célèbre tour de magie implique qu'un interprète chante une note en direction d'un verre de cristal jusqu'à ce que le verre se brise. Expliquez pourquoi l'astuce fonctionne en termes de résonance et de fréquence naturelle.