7.4 : Théorème travail-énergie
- Page ID
- 191524
- Appliquez le théorème travail-énergie pour trouver des informations sur le mouvement d'une particule, compte tenu des forces qui agissent sur elle
- Utilisez le théorème travail-énergie pour trouver des informations sur les forces agissant sur une particule, en fonction de son mouvement
Nous avons discuté de la manière de déterminer le travail effectué sur une particule par les forces qui agissent sur elle, mais comment ce travail se manifeste-t-il dans le mouvement de la particule ? Selon la deuxième loi du mouvement de Newton, la somme de toutes les forces agissant sur une particule, ou la force nette, détermine le taux de variation de la quantité de mouvement de la particule, ou de son mouvement. Par conséquent, nous devons examiner le travail effectué par toutes les forces agissant sur une particule, ou le réseau, pour voir quel effet cela a sur le mouvement de la particule.
Commençons par examiner le réseau effectué sur une particule lorsqu'elle se déplace sur un déplacement infinitésimal, qui est le produit scalaire de la force nette et du déplacement :
\[dW_{net} = \vec{F}_{net} \cdotp d \vec{r}. \nonumber\]
La deuxième loi de Newton nous dit que
\[\vec{F}_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \nonumber\]
donc
\[dW_{net} = m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r}. \nonumber\]
Pour les fonctions mathématiques décrivant le mouvement d'une particule physique, nous pouvons réarranger les différentiels dt, etc., sous forme de quantités algébriques dans cette expression, c'est-à-dire
\[\begin{align*} dW_{net} &= m \left(\dfrac{d \vec{v}}{dt}\right) \cdotp d \vec{r} \\[4pt] &= m\, d \vec{v}\; \cdotp \left(\dfrac{d \vec{r}}{dt}\right) \\[4pt] &= m \vec{v}\; \cdotp d \vec{v}, \end{align*}\]
où nous avons substitué la vitesse à la dérivée temporelle du déplacement et utilisé la propriété commutative du produit scalaire. Comme les dérivées et les intégrales des scalaires vous sont probablement plus familières à ce stade, nous exprimons le produit scalaire en termes de coordonnées cartésiennes avant de procéder à l'intégration entre deux points A et B sur la trajectoire de la particule. Cela nous donne le travail réseau effectué sur la particule :
\[\begin{align} W_{net,\; AB} & = \int_{A}^{B} (mv_{x} dv_{x} + mv_{y}dv_{y} + mv_{z}dv_{z} \\[4pt] & = \frac{1}{2} m \left| v_{x}^{2} + v_{y}^{2} + v_{z}^{2} \right|_{A}^{B} = \left|\frac{1}{2} mv^{2} \right|_{A}^{B} = K_{B} - K_{A} \ldotp \end{align} \label{7.8}\]
Dans l'étape intermédiaire, nous avons utilisé le fait que le carré de la vitesse est la somme des carrés de ses composantes cartésiennes, et dans la dernière étape, nous avons utilisé la définition de l'énergie cinétique de la particule. Ce résultat important s'appelle le théorème travail-énergie.
Le réseau effectué sur une particule est égal à la variation de l'énergie cinétique de la particule :
\[W_{net} = K_{B} - K_{A} \ldotp \label{7.9}\]

Selon ce théorème, lorsqu'un objet ralentit, son énergie cinétique finale est inférieure à son énergie cinétique initiale, la variation de son énergie cinétique est négative, de même que le travail en réseau effectué sur celui-ci. Si un objet accélère, le réseau effectué sur celui-ci est positif. Lors du calcul du réseau, vous devez inclure toutes les forces qui agissent sur un objet. Si vous omettez des forces qui agissent sur un objet, ou si vous incluez des forces qui n'agissent pas sur celui-ci, vous obtiendrez un mauvais résultat.
L'importance du théorème travail-énergie, et des autres généralisations auxquelles il conduit, est qu'il rend certains types de calculs beaucoup plus simples à réaliser qu'ils ne le seraient en essayant de résoudre la deuxième loi de Newton. Par exemple, dans la section sur les lois du mouvement de Newton, nous avons trouvé la vitesse d'un objet glissant sur un plan sans friction en résolvant la deuxième loi de Newton pour l'accélération et en utilisant des équations cinématiques pour une accélération constante, obtenant
\[v_{f}^{2} = v_{i}^{2} + 2g(s_{f} - s_{i}) \sin \theta,\]
où\(s\) est le déplacement vers le bas de l'avion.
Nous pouvons également obtenir ce résultat à partir du théorème travail-énergie (Équation \ ref {7.9}). Comme seules deux forces agissent sur l'objet, la gravité et la force normale, et que la force normale ne fait aucun travail, le réseau est simplement le travail effectué par gravité. Cela dépend uniquement du poids de l'objet et de la différence de hauteur, donc
\[W_{net} = W_{grav} = -mg (y_{f} - y_{i}),\]
où\(y\) est positif vers le haut. Le théorème de l'énergie de travail indique que cela équivaut à la variation de l'énergie cinétique :
\[-mg (y_{f} - y_{i}) = \frac{1}{2} (v_{f}^{2} - v_{i}^{2}) \ldotp\]
En utilisant un triangle droit, nous pouvons voir que
\[(y_f − y_i) = (s_f − s-i)\sin \theta, \nonumber\]
le résultat pour la vitesse finale est donc le même.
Quels sont les avantages de l'utilisation du théorème travail-énergie ? La réponse est que pour une surface plane sans friction, pas grand-chose. Cependant, la deuxième loi de Newton est facile à résoudre uniquement dans ce cas particulier, alors que le théorème de l'énergie de travail donne la vitesse finale pour n'importe quelle forme de surface sans friction. Pour une surface incurvée arbitraire, la force normale n'est pas constante et la deuxième loi de Newton peut être difficile, voire impossible, à résoudre de manière analytique. Constante ou pas, pour un mouvement le long d'une surface, la force normale ne fonctionne jamais, car elle est perpendiculaire au déplacement. Un calcul utilisant le théorème travail-énergie évite cette difficulté et s'applique à des situations plus générales.
- Dessinez un diagramme du corps libre pour chaque force exercée sur l'objet.
- Déterminez si chaque force agit sur le déplacement dans le diagramme. Assurez-vous de garder tout signe positif ou négatif dans le travail effectué.
- Additionnez la quantité totale de travail effectuée par chaque force.
- Définissez ce travail total comme égal à la variation de l'énergie cinétique et résolvez tout paramètre inconnu.
- Vérifiez vos réponses. Si l'objet se déplace à une vitesse constante ou à une accélération nulle, le travail total effectué doit être nul et correspondre à la variation de l'énergie cinétique. Si le travail total est positif, l'objet doit avoir accéléré ou augmenté son énergie cinétique. Si le travail total est négatif, l'énergie cinétique de l'objet doit avoir ralenti ou diminué
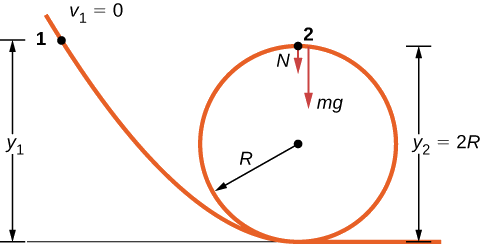
La piste sans friction pour une petite voiture comprend un rayon en boucle\(R\). À quelle hauteur, mesurée à partir du bas de la boucle, la voiture doit-elle être placée pour partir de l'arrêt sur le tronçon de voie qui approche et faire le tour de la boucle ?
Stratégie
Le diagramme du corps libre à la position finale de l'objet est dessiné sur la figure\(\PageIndex{2}\). Le travail gravitationnel est le seul travail effectué sur le déplacement qui n'est pas nul. Comme le poids pointe dans la même direction que le déplacement vertical net, le travail total effectué par la force gravitationnelle est positif. À partir du théorème travail-énergie, la hauteur de départ détermine la vitesse de la voiture en haut de la boucle,
\[mg(y_{2} - y_{1}) = \dfrac{1}{2} mv_{2}^{2}, \nonumber\]
où la notation est illustrée dans la figure ci-jointe. Au sommet de la boucle, la force normale et la gravité sont à la fois inférieures et l'accélération est centripète, donc
\[a_{top} = \dfrac{F}{m} = \dfrac{N + mg}{m} = \frac{v_{2}^{2}}{R} \ldotp \nonumber\]
La condition pour maintenir le contact avec la voie est qu'il doit y avoir une force normale, aussi légère soit-elle, c'est-à-dire\(N > 0\). En remplaçant\(v_{2}^{2}\) et\(N\), nous pouvons trouver la condition pour\(y_1\).
Solution
Mettez en œuvre les étapes de la stratégie pour obtenir le résultat souhaité :
\[N = -mg + \frac{mv_{2}^{2}}{R} = \frac{-mgR + 2mg(y_{1} - 2R)}{R} > 0\; or\; y_{1} > \frac{5R}{2} \ldotp \nonumber\]
L'importance
À la surface de la boucle, la composante normale de la gravité et la force de contact normale doivent fournir l'accélération centripète de la voiture qui fait le tour de la boucle. La composante tangentielle de la gravité ralentit ou accélère la voiture. Un enfant apprendrait à quelle hauteur démarrer la voiture par essais et erreurs, mais maintenant que vous connaissez le théorème de l'énergie travail-énergie, vous pouvez prédire la hauteur minimale (ainsi que d'autres résultats plus utiles) à partir de principes physiques. En utilisant le théorème de l'énergie travail-travail, vous n'avez pas eu à résoudre d'équation différentielle pour déterminer la hauteur.
Supposons que le rayon de la boucle dans l'exemple\(\PageIndex{1}\) soit de 15 cm et que la petite voiture part de l'arrêt à une hauteur de 45 cm au-dessus du bas. Quelle est sa vitesse en haut de la boucle ?
Dans les situations où le mouvement d'un objet est connu, mais où les valeurs d'une ou de plusieurs des forces agissant sur celui-ci ne sont pas connues, vous pouvez utiliser le théorème de l'énergie de travail pour obtenir des informations sur les forces. Le travail dépend de la force et de la distance sur laquelle il agit, de sorte que les informations sont fournies via leur produit.
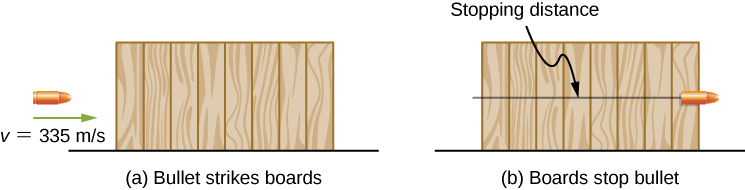
Une balle a une masse de 40 grains (2,60 g) et une vitesse initiale de 1100 pieds. /s (335 m/s). Il peut pénétrer huit planches de pin de 1 pouce, chacune d'une épaisseur de 0,75 pouce. Quelle est la force de freinage moyenne exercée par le bois, comme le montre la figure\(\PageIndex{3}\) ?
Stratégie
Nous pouvons supposer que dans les conditions générales énoncées, la balle perd toute son énergie cinétique en pénétrant les planches. Le théorème de l'énergie de travail indique donc que son énergie cinétique initiale est égale à la force d'arrêt moyenne multipliée par la distance parcourue. La variation de l'énergie cinétique de la balle et le réseau effectué pour l'arrêter sont tous deux négatifs. Ainsi, lorsque vous écrivez le théorème de l'énergie de travail, avec un réseau égal à la force moyenne multipliée par la distance d'arrêt, c'est ce que vous obtenez. L'épaisseur totale des huit planches de pin de 1 pouce\(\frac{3}{4}\) dans lesquelles la balle pénètre est de 8 x po = 6 po = 15,2 cm.
Solution
En appliquant le théorème travail-énergie, nous obtenons
\[W_{net} = - F_{ave} \Delta s_{stop} = - K_{initial} , \nonumber\]
donc
\[F_{ave} = \frac{\frac{1}{2} mv^{2}}{\Delta s_{stop}} = \frac{\frac{1}{2} (2.66 \times 10^{-3}\; kg)(335\; m/s)^{2}}{0.152\; m} = 960\; N \ldotp \nonumber\]
L'importance
Nous aurions pu utiliser la deuxième loi et la cinématique de Newton dans cet exemple, mais le théorème travail-énergie fournit également une réponse à des situations moins simples. La pénétration d'une balle tirée verticalement vers le haut dans un bloc de bois est abordée dans une section du récent article d'Asif Shakur [« Bullett-Block Science Video Puzzle ». Le professeur de physique (janvier 2015) 53 (1) : 15-16]. Si la balle est tirée au point mort dans le bloc, elle perd toute son énergie cinétique et pénètre légèrement plus loin que si elle est tirée hors centre. La raison en est que si la balle frappe de manière décentrée, elle dégage un peu d'énergie cinétique une fois qu'elle arrête de pénétrer, car le bloc tourne. Le théorème de l'énergie de travail implique qu'une plus faible variation de l'énergie cinétique entraîne une pénétration plus faible. Vous en saurez plus sur la physique dans cet article intéressant une fois que vous aurez fini de lire Momentum angulaire.
Apprenez-en plus sur le travail et l'énergie dans cette simulation PhET (https://phet.colorado.edu/en/simulation/the-ramp) appelée « la rampe ». Essayez de modifier la force qui pousse la boîte et la force de friction le long de l'inclinaison. Les diagrammes de travail et d'énergie peuvent être examinés pour noter le travail total effectué et la variation de l'énergie cinétique de la boîte.


