Skip to main content
Global

4.6 : Mouvement relatif en une et deux dimensions

  1. Last updated
  2. Save as PDF
  • Page ID
    191545

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Expliquer le concept de cadres de référence.
    • Écrivez les équations vectorielles de position et de vitesse pour le mouvement relatif.
    • Dessinez les vecteurs de position et de vitesse pour le mouvement relatif.
    • Analysez les problèmes de mouvement relatif unidimensionnels et bidimensionnels en utilisant les équations vectorielles de position et de vitesse.

    Le mouvement ne se produit pas de manière isolée. Si vous voyagez dans un train qui circule à 10 m/s vers l'est, cette vitesse est mesurée par rapport au sol sur lequel vous voyagez. Toutefois, si un autre train vous dépasse à 15 m/s vers l'est, votre vitesse par rapport à cet autre train est différente de votre vitesse par rapport au sol. Votre vitesse par rapport à l'autre train est de 5 m/s vers l'ouest. Pour approfondir cette idée, nous devons d'abord établir une terminologie.

    Cadres de référence

    Pour discuter du mouvement relatif dans une ou plusieurs dimensions, nous introduisons d'abord le concept de repères. Lorsque nous disons qu'un objet a une certaine vitesse, nous devons indiquer qu'il a une vitesse par rapport à un référentiel donné. Dans la plupart des exemples que nous avons examinés jusqu'à présent, ce référentiel a été la Terre. Si vous dites qu'une personne est assise dans un train qui se déplace à 10 m/s vers l'est, vous sous-entendez que la personne à bord du train se déplace par rapport à la surface de la Terre à cette vitesse, et que la Terre est le repère de référence. Nous pouvons élargir notre vision du mouvement de la personne à bord du train et dire que la Terre tourne sur son orbite autour du Soleil, auquel cas le mouvement devient plus compliqué. Dans ce cas, le système solaire est le référentiel. En résumé, toute discussion sur le mouvement relatif doit définir les repères de référence concernés. Nous développons maintenant une méthode pour faire référence à des repères de référence en mouvement relatif.

    Mouvement relatif dans une dimension

    Nous introduisons d'abord le mouvement relatif dans une dimension, car les vecteurs de vitesse simplifient le fait qu'ils n'ont que deux directions possibles. Prenons l'exemple de la personne assise dans un train qui se déplace vers l'est. Si nous choisissons l'est comme direction positive et la Terre comme repère, alors nous pouvons écrire la vitesse du train par rapport à la Terre comme\(\vec{v}_{TE}\) = 10 m/s\(\hat{i}\) est, où les indices TE se réfèrent au train et à la Terre. Supposons maintenant que la personne se lève de son siège et marche vers l'arrière du train à une vitesse de 2 m/s. Cela nous indique qu'elle a une vitesse par rapport au référentiel du train. Comme la personne marche vers l'ouest, dans la direction négative, nous écrivons sa vitesse par rapport au train comme suit\(\vec{v}_{PT}\) = −2 m/s\(\hat{i}\). Nous pouvons ajouter les deux vecteurs de vitesse pour trouver la vitesse de la personne par rapport à la Terre. Cette vitesse relative s'écrit

    \[\vec{v}_{PE} = \vec{v}_{PT} + \vec{v}_{TE} \ldotp \label{4.33}\]

    Notez l'ordre des indices pour les différents référentiels dans l'équation \ ref {4.33}. Les indices du référentiel de couplage, qui est le train, apparaissent consécutivement dans la partie droite de l'équation. La figure\(\PageIndex{1}\) montre l'ordre correct des indices lors de la formation de l'équation vectorielle.

    alt
    Figure\(\PageIndex{1}\) : Lors de la construction de l'équation vectorielle, les indices du référentiel de couplage apparaissent consécutivement à l'intérieur. Les indices du côté gauche de l'équation sont les mêmes que les deux indices extérieurs du côté droit de l'équation.

    En additionnant les vecteurs, on trouve\(\vec{v}_{PE}\) = 8 m/s\(\hat{i}\), donc la personne se déplace à 8 m/s vers l'est par rapport à la Terre. Cela est illustré graphiquement sur la figure\(\PageIndex{2}\).

    Vecteurs de vitesse du train par rapport à la Terre, de la personne par rapport au train et de la personne par rapport à la Terre. V sub T E est le vecteur de vitesse du train par rapport à la Terre. Elle a une valeur de 10 mètres par seconde et est représentée par une longue flèche verte pointant vers la droite. V sub P T est le vecteur de vitesse de la personne par rapport au train. Il a une valeur de -2 mètres par seconde et est représenté par une courte flèche verte pointant vers la gauche. V sub P E est le vecteur de vitesse de la personne par rapport à la Terre. Elle a une valeur de 8 mètres par seconde et est représentée par une flèche verte de longueur moyenne pointant vers la droite.
    Figure\(\PageIndex{2}\) : Vecteurs de vitesse du train par rapport à la Terre, de la personne par rapport au train et de la personne par rapport à la Terre.

    Vitesse relative en deux dimensions

    Nous pouvons maintenant appliquer ces concepts à la description du mouvement en deux dimensions. Considérons une particule P et les repères de référence S et S', comme indiqué sur la figure\(\PageIndex{3}\). La position de l'origine de S'telle que mesurée en S est\(\vec{r}_{S'S}\), la position de P telle que mesurée en S'est\(\vec{r}_{PS'}\), et la position de P telle que mesurée en S est\(\vec{r}_{PS}\).

    Un système de coordonnées x y z est affiché et étiqueté comme système S. Un second système de coordonnées, S premier avec des axes x premier, y premier, z premier, est décalé par rapport à S. Le vecteur r sub S prime, représenté par une flèche violette, s'étend de l'origine de S à l'origine de S à l'origine de S premier. Le vecteur r sub P S est un vecteur allant de l'origine de S à un point P. Le vecteur r sub P S prime est un vecteur allant de l'origine de S prime au même point P. Les vecteurs r s prime s, r P S prime et r P S forment un triangle, et r P S est la somme vectorielle de r S prime S et r P S prime.
    Figure\(\PageIndex{3}\) : Les positions de la particule P par rapport aux trames S\(\vec{r}_{PS}\) et\(\vec{r}_{PS'}\) S'sont respectivement.

    Sur la figure,\(\PageIndex{3}\) nous voyons que

    \[\vec{r}_{PS} = \vec{r}_{PS} + \vec{r}_{S'S} \ldotp \label{4.34}\]

    Les vitesses relatives sont les dérivées temporelles des vecteurs de position. Par conséquent,

    \[\vec{v}_{PS} = \vec{v}_{PS'} + \vec{v}_{S'S} \ldotp \label{4.35}\]

    La vitesse d'une particule par rapport à S est égale à sa vitesse par rapport à S'plus la vitesse de S'par rapport à S.

    Nous pouvons étendre l'équation \ ref {4.35} à n'importe quel nombre de cadres de référence. Pour les particules P avec des vitesses\(\vec{v}_{PA}\)\(\vec{v}_{PB}\), et\(\vec{v}_{PC}\) dans les cadres A, B et C,

    \[\vec{v}_{PC} = \vec{v}_{PA} + \vec{v}_{AB} + \vec{v}_{BC} \ldotp \label{4.36}\]

    Nous pouvons également voir comment les accélérations sont liées, telles qu'elles sont observées dans deux cadres de référence, en différenciant l'équation \ ref {4.35} :

    \[\vec{a}_{PS} = \vec{a}_{PS'} + \vec{a}_{S'S} \ldotp \label{4.37}\]

    Nous voyons que si la vitesse de S'par rapport à S est constante, alors\(\vec{a}_{S'S}\) = 0 et

    \[\vec{a}_{PS} = \vec{a}_{PS'} \ldotp \label{4.38}\]

    Cela signifie que l'accélération d'une particule est la même que celle mesurée par deux observateurs se déplaçant à une vitesse constante l'un par rapport à l'autre.

    Exemple 4.13 : Mouvement d'une voiture par rapport à un camion

    Un camion roule vers le sud à une vitesse de 70 km/h en direction d'une intersection. Une voiture roule vers l'est en direction de l'intersection à une vitesse de 80 km/h (Figure\(\PageIndex{4}\)). Quelle est la vitesse de la voiture par rapport au camion ?

    Un camion est représenté se dirigeant vers le sud à une vitesse V sous T E de 70 km/h en direction d'une intersection. Une voiture roule vers l'est en direction de l'intersection à une vitesse V sous C E de 80 km/h
    Figure\(\PageIndex{4}\) : Une voiture se déplace vers l'est en direction d'une intersection tandis qu'un camion se déplace vers le sud vers la même intersection.

    Stratégie

    Tout d'abord, nous devons établir le référentiel commun aux deux véhicules, à savoir la Terre. Ensuite, nous écrivons les vitesses de chacune par rapport au référentiel de la Terre, ce qui nous permet de former une équation vectorielle qui relie la voiture, le camion et la Terre afin de déterminer la vitesse de la voiture par rapport au camion.

    Solution

    La vitesse de la voiture par rapport à la Terre est de\(\vec{v}_{CE}\) = 80 km/h\(\hat{i}\). La vitesse du camion par rapport à la Terre est\(\vec{v}_{TE}\) = −70 km/h\(\hat{j}\). En utilisant la règle d'addition de vitesse, l'équation du mouvement relatif que nous recherchons est

    \[\vec{v}_{CT} = \vec{v}_{CE} + \vec{v}_{ET} \ldotp \label{ex2}\]

    \(\vec{v}_{CT}\)Voici la vitesse de la voiture par rapport au camion, et la Terre est le repère de connexion. Puisque nous avons la vitesse du camion par rapport à la Terre, le négatif de ce vecteur est la vitesse de la Terre par rapport au camion :\(\vec{v}_{ET} = − \vec{v}_{TE}\). Le diagramme vectoriel de cette équation est illustré à la figure\(\PageIndex{5}\).

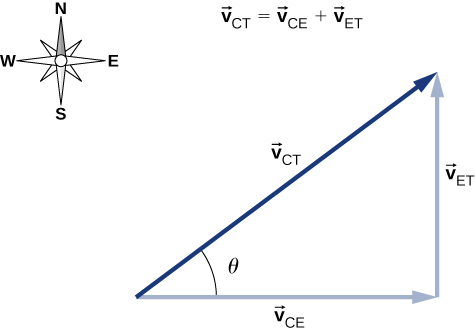
    Le triangle droit formé par les vecteurs V sub C E vers la droite, V sub E T vers le bas et V sub C T vers le haut et vers la droite est représenté. V sub C T est l'hypoténuse et fait un angle de thêta avec V sub C E. Le vecteur d'équation vectorielle v sub C T est égal au vecteur C E plus le vecteur E plus le vecteur E T est donné. Une boussole indique le nord vers le haut, l'est vers la droite, le sud vers le bas et l'ouest vers la gauche.
    Figure\(\PageIndex{5}\) : Diagramme vectoriel de l'équation vectorielle \ ref {ex2}.

    Nous pouvons maintenant déterminer la vitesse de la voiture par rapport au camion :

    \[\big| \vec{v}_{CT} \big| = \sqrt{(80.0\; km/h)^{2} + (70.0\; km/h)^{2}} = 106.\; km/h \nonumber\]

    et

    \[\theta = \tan^{-1} \left(\dfrac{70.0}{80.0}\right) = 41.2^{o}\; north\; of\; east \ldotp \nonumber\]

    L'importance

    Dessiner un diagramme vectoriel montrant les vecteurs de vitesse peut aider à comprendre la vitesse relative des deux objets.

    Exercice 4.6

    Un bateau se dirige vers le nord en eau calme à 4,5 m/s directement à travers une rivière qui coule vers l'est à 3 m/s. Quelle est la vitesse du bateau par rapport à la Terre ?

    Exemple 4.14 : Piloter un avion dans un vent

    Un pilote doit piloter son avion plein nord pour atteindre sa destination. L'avion peut voler à 300 km/h dans l'air calme. Un vent souffle du nord-est à 90 km/h. (a) Quelle est la vitesse de l'avion par rapport au sol ? (b) Dans quelle direction la pilote doit-elle diriger son avion pour voler plein nord ?

    Stratégie

    La pilote doit pointer son avion un peu à l'est par rapport au nord pour compenser la vitesse du vent. Nous devons construire une équation vectorielle qui contient la vitesse de l'avion par rapport au sol, la vitesse de l'avion par rapport à l'air et la vitesse de l'air par rapport au sol. Ces deux dernières grandeurs étant connues, nous pouvons déterminer la vitesse de l'avion par rapport au sol. Nous pouvons représenter graphiquement les vecteurs et utiliser ce diagramme pour évaluer l'amplitude de la vitesse de l'avion par rapport au sol. Le diagramme nous indiquera également l'angle que fait la vitesse de l'avion avec le nord par rapport à l'air, c'est-à-dire la direction dans laquelle la pilote doit prendre la tête de son avion.

    Solution

    L'équation vectorielle est\(\vec{v}_{PG} = \vec{v}_{PA} + \vec{v}_{AG}\) la suivante : P = plan, A = air et G = sol. À partir de la géométrie de la figure\(\PageIndex{6}\), nous pouvons facilement déterminer l'amplitude de la vitesse de l'avion par rapport au sol et l'angle de cap de l'avion\(\theta\).

    Une boussole indique que le nord se trouve en haut, de l'est vers la droite, du sud vers le bas et de l'ouest vers la gauche. Les vecteurs V sub P G, V sub A G et V sub P A forment un triangle. Un avion est représenté sur le vecteur V sous P G, qui pointe vers le haut. V sub P A pointe vers le haut et vers la droite, à un angle de thêta par rapport au vecteur V sub P G. V sub A G pointe vers le bas et vers la gauche, à un angle de 45 degrés sous l'horizontale. V sub P G est la somme vectorielle de v sub P A et V sub A G.
    Figure\(\PageIndex{6}\) : Diagramme vectoriel pour l'équation \ ref {4.34} montrant les vecteurs\(\vec{v}_{PA}\)\(\vec{v}_{AG}\), et\(\vec{v}_{PG}\).
    1. Quantités connues : $$ \ big| \ vec {v} _ {PA} \ big| = 300 \ ; km/h$$ $$ \ big| \ vec {v} _ {AG} \ big| = 90 \ ; km/H$$En remplaçant dans l'équation du mouvement, nous obtenons\(\big| \vec{v}_{PG} \big|\) = 230 km/h.
    2. L'angle\(\theta\) = tan −1\(\left(\dfrac{63.64}{300}\right)\) = 12° à l'est du nord.