4.5 : Mouvement circulaire uniforme

Last updated
Save as PDF

Page ID: 191547

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Résolvez l'accélération centripète d'un objet se déplaçant sur une trajectoire circulaire.
Utilisez les équations du mouvement circulaire pour déterminer la position, la vitesse et l'accélération d'une particule exécutant un mouvement circulaire.
Expliquez les différences entre l'accélération centripète et l'accélération tangentielle résultant d'un mouvement circulaire non uniforme.
Évaluez l'accélération centripète et tangentielle dans un mouvement circulaire non uniforme et trouvez le vecteur d'accélération total.

Le mouvement circulaire uniforme est un type de mouvement spécifique dans lequel un objet se déplace en cercle à une vitesse constante. Par exemple, tout point d'une hélice qui tourne à une vitesse constante exécute un mouvement circulaire uniforme. Les aiguilles des secondes, des minutes et des heures d'une montre en sont d'autres exemples. Il est remarquable que les points de ces objets en rotation accélèrent réellement, bien que la vitesse de rotation soit constante. Pour cela, il faut analyser le mouvement en termes de vecteurs.

Accélération centripète

En cinématique unidimensionnelle, les objets à vitesse constante n'ont aucune accélération. Cependant, en cinématique bidimensionnelle et tridimensionnelle, même si la vitesse est constante, une particule peut avoir une accélération si elle se déplace le long d'une trajectoire courbe telle qu'un cercle. Dans ce cas, le vecteur de vitesse change, ou\(\frac{d\vec{v}}{dt}\) ≥0. Ceci est illustré dans la figure\(\PageIndex{1}\). Lorsque la particule se déplace dans le sens antihoraire dans le temps\(\Delta\) t sur la trajectoire circulaire, son vecteur de position se déplace de\(\vec{r}(t)\) à\(\vec{r}(t + \Delta t)\). Le vecteur de vitesse a une amplitude constante et est tangent à la trajectoire lorsqu'il passe de\(\vec{v}\) (t) à\(\vec{v}\left(t + \Delta t\right)\), en changeant uniquement de direction. Comme le vecteur de vitesse\(\vec{v}(t)\) est perpendiculaire au vecteur de position\(\vec{r}\) (t), les triangles formés par les vecteurs de position et les vecteurs de vitesse et\(\Delta \vec{v}\) sont similaires.\(\Delta \vec{r}\) En outre, puisque

\[|\vec{r}(t) | = | \vec{r} (t + \Delta t)| \nonumber\]

\[| \vec{v} (t)| = | \vec{v} (t + \Delta t)|, \nonumber \]

les deux triangles sont isocèles. À partir de ces faits, nous pouvons faire l'affirmation

\[\dfrac{\Delta v}{v} = \dfrac{\Delta r}{r}\]

\[\Delta v = \dfrac{v}{r} \Delta r.\]

La figure a montre un cercle dont le centre est situé au point C. On y voit le rayon r de t et le rayon r de t, qui sont séparés par un angle Delta thêta, et la longueur de corde delta r reliant les extrémités des deux rayons. Les vecteurs r de t, r de t plus delta t et delta r forment un triangle. À l'extrémité du vecteur r de t, la vitesse est représentée par v de t et pointe vers le haut et vers la droite, tangente au cercle. À la pointe du vecteur r de t plus delta t, la vitesse est représentée par v de t plus delta t et pointe vers le haut et vers la gauche, tangente au cercle. La figure b montre les vecteurs v de t et v de t plus delta t avec leurs queues jointes, et le vecteur delta v de la pointe de v à la pointe de v de t plus delta t. Ces trois vecteurs forment un triangle. L'angle entre le v de t et le v de t plus le delta t est thêta. — Figure\(\PageIndex{1}\) : (a) Une particule se déplace en cercle à une vitesse constante, avec des vecteurs de position et de vitesse à des moments\(t\) et\(t + \Delta t\). (b) Vecteurs de vitesse formant un triangle. Les deux triangles de la figure sont similaires. Le vecteur\(\Delta \vec{v}\) pointe vers le centre du cercle dans la limite\(\Delta t → 0.\)

Nous pouvons trouver l'ampleur de l'accélération à partir de

\[a = \lim_{\Delta t \rightarrow 0} \left(\dfrac{\Delta v}{\Delta t}\right) = \frac{v}{r} \left(\lim_{\Delta t \rightarrow 0} \dfrac{\Delta r}{\Delta t}\right) = \frac{v^{2}}{r} \ldotp\]

La direction de l'accélération peut également être déterminée en notant que lorsque\(\Delta\) t et donc s'\(\Delta \theta\)approche de zéro, le vecteur\(\Delta \vec{v}\) s'approche d'une direction perpendiculaire à\(\vec{v}\). Dans la limite\(\Delta t → 0,\)\(\Delta \vec{v}\) est perpendiculaire à\(\vec{v}\). Comme elle\(\vec{v}\) est tangente au cercle, l'accélération\(\frac{d \vec{v}}{dt}\) pointe vers le centre du cercle. En résumé, une particule se déplaçant en cercle à une vitesse constante a une accélération de magnitude

\[a_{c} = \frac{v^{2}}{r} \ldotp \label{4.27}\]

La direction du vecteur d'accélération se situe vers le centre du cercle (Figure\(\PageIndex{2}\)). Il s'agit d'une accélération radiale appelée accélération centripète, c'est pourquoi nous lui donnons l'indice\(c\). Le mot centripète vient des mots latins centrum (qui signifie « centre ») et petere (qui signifie « chercher »), et prend donc le sens de « recherche du centre ».

Un cercle est représenté par une flèche violette étiquetée comme vecteur a sub c pointant radialement vers l'intérieur et une flèche verte tangente au cercle et étiquetée v. Les flèches sont représentées avec leur queue au même point sur le cercle. — Figure\(\PageIndex{2}\) : Le vecteur d'accélération centripète pointe vers le centre de la trajectoire circulaire du mouvement et représente une accélération dans la direction radiale. Le vecteur de vitesse est également affiché et est tangent au cercle.

Examinons quelques exemples illustrant les magnitudes relatives de la vitesse, du rayon et de l'accélération centripète.

Exemple\(\PageIndex{1}\): Creating an Acceleration of 1 g

Un jet vole à 134,1 m/s le long d'une ligne droite et effectue un virage sur une trajectoire circulaire au niveau du sol. Quel doit être le rayon du cercle pour produire une accélération centripète de 1 g sur le pilote et le jet vers le centre de la trajectoire circulaire ?

Stratégie

Compte tenu de la vitesse du jet, nous pouvons déterminer le rayon du cercle dans l'expression de l'accélération centripète.

Solution

Réglez l'accélération centripète égale à l'accélération de la gravité : 9,8 m/s ² =\(\frac{v^{2}}{r}\).

En résolvant le rayon, nous trouvons

\[r = \frac{(134.1\; m/s)^{2}}{9.8\; m/s^{2}} = 1835\; m = 1.835\; km \ldotp\]

L'importance

Pour créer une accélération supérieure à g sur le pilote, le jet devrait soit diminuer le rayon de sa trajectoire circulaire, soit augmenter sa vitesse sur sa trajectoire existante, soit les deux.

Exercice 4.5

Un volant a un rayon de 20,0 cm. Quelle est la vitesse d'un point situé sur le bord du volant s'il subit une accélération centripète de 900,0 cm/s ² ?

L'accélération centripète peut avoir une large gamme de valeurs, en fonction de la vitesse et du rayon de courbure de la trajectoire circulaire. Les accélérations centripètes typiques sont données dans le tableau\(\PageIndex{1}\).

Tableau\(\PageIndex{1}\) : Accélérations centripètes typiques
Objet	Accélération centripète (m/s ² ou facteurs de g)
La Terre autour du Soleil	5,93 x 10 ^-3
Lune autour de la Terre	2,73 x 10 ^-3
Satellite en orbite géosynchrone	0,233
Bord extérieur d'un CD lors de la lecture	5,75
Un jet dans un tonneau	(2 à 3 g)
montagnes russes	(5 g)
Électron en orbite autour d'un proton dans un modèle simple de Bohr de l'atome	9,0 x 10 ²²

Équations du mouvement pour un mouvement circulaire uniforme

Une particule qui exécute un mouvement circulaire peut être décrite par son vecteur de position\(\vec{r}(t)\). La figure\(\PageIndex{3}\) montre une particule exécutant un mouvement circulaire dans le sens antihoraire. Lorsque la particule se déplace sur le cercle, son vecteur de position balaie l'angle\(\theta\) avec l'axe X. Le vecteur\(\vec{r}(t)\) formant un angle\(\theta\) avec l'axe X est représenté avec ses composantes le long des axes X et Y. L'amplitude du vecteur de position est\(A = |\vec{r}(t)|\) et est également le rayon du cercle, de sorte qu'en termes de ses composantes,

\[\vec{r} (t) = A \cos \omega \hat{i} + A \sin \omega t \hat{j} \ldotp \label{4.28}\]

\(\omega\)Voici une constante appelée fréquence angulaire de la particule. La fréquence angulaire est exprimée en unités de radians (rad) par seconde et est simplement le nombre de radians de mesure angulaire par lesquels passe la particule par seconde. L'angle\(θ\) que possède le vecteur de position à un moment donné est\(\omega\) t.

Si\(T\) c'est la période de mouvement, ou le temps nécessaire pour effectuer un tour (\(2 \pi\, rad\)), alors

Un rayon de cercle r, centré sur l'origine d'un système de coordonnées x y est affiché. Le rayon r de t est un vecteur allant de l'origine à un point du cercle et fait un angle thêta égal à oméga t par rapport à l'horizontale. La composante x du vecteur r est la magnitude de r de t fois le cosinus de l'oméga t. La composante y du vecteur r est la magnitude de r de t fois le sinus de l'oméga t. La circulation se fait dans le sens antihoraire autour du cercle. — Figure\(\PageIndex{3}\) : Le vecteur de position d'une particule en mouvement circulaire avec ses composantes le long des axes x et y. La particule se déplace dans le sens antihoraire. L'angle\(\theta\) est la fréquence angulaire\(\omega\) en radians par seconde multipliée par\(t\).

La vitesse et l'accélération peuvent être obtenues à partir de la fonction de position par différenciation :

\[\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \omega t \hat{j} \ldotp \label{4.29}\]

La figure montre\(\PageIndex{3}\) que le vecteur de vitesse est tangent au cercle à l'emplacement de la particule, avec une magnitude\(\omega\) A. De même, le vecteur d'accélération est trouvé en différenciant la vitesse :

\[\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = -A \omega^{2} \cos \omega t \hat{i} - A \omega^{2} \sin \omega t \hat{j} \ldotp \label{4.30}\]

À partir de cette équation, nous voyons que le vecteur d'accélération a une magnitude A\(\omega^{2}\) et est dirigé à l'opposé du vecteur de position, vers l'origine, car\(\vec{a}\) (t) = −\(\omega^{2} \vec{r}\) (t).

Exemple\(\PageIndex{2}\): Circular Motion of a Proton

Un proton a une vitesse de 5 x 10 ⁶ m/s et se déplace en cercle dans le plan xy de rayon r = 0,175 m. Quelle est sa position dans le plan xy au temps t = 2,0 x 10 ⁻⁷ s = 200 ns ? À t = 0, la position du proton est de 0,175 m\(\hat{i}\) et il tourne dans le sens antihoraire. Esquissez la trajectoire.

Solution

À partir des données fournies, le proton a une période et une fréquence angulaire :

\[T = \frac{2 \pi r}{v} = \frac{2 \pi (0.175\; m)}{5.0 \times 10^{6}\; m/s} = 2.20 \times 10^{-7}\; s \nonumber \]

\[\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2.20 \times 10^{-7}\; s} = 2.856 \times 10^{7}\; rad/s \ldotp \nonumber \]

La position de la particule à t = 2,0 x 10 ⁻⁷ s avec A = 0,175 m est

\[\begin{align*} \vec{r} (2.0 \times 10^{-7}\; s) & = A \cos \omega (2.0 \times 10^{-7}\; s) \hat{i} + A \sin \omega (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{i} + 0.175 \sin (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (5.712\; rad) \hat{i} + 0.175 \sin (5.172\; rad) \hat{j}\; m \\ & = 0.147 \hat{i} - 0.095 \hat{j}\; m \ldotp \end{align*}\]

À partir de ce résultat, nous voyons que le proton est situé légèrement en dessous de l'axe X. Ceci est illustré dans la figure\(\PageIndex{4}\).

Un graphique de la position y en fonction de la position x est affiché. x et y sont mesurés en mètres et vont de -0,2 à 0,2. Un proton se déplace dans un cercle dans le sens inverse des aiguilles d'une montre centré sur l'origine est représenté à 11 moments différents. À t = 0 s, la particule est à x = 0,175 m et y = 0. À t = 200 nanosecondes, la particule se trouve à une position donnée par le vecteur 0,147 I hat moins 0,95 j hat mètres. — Figure\(\PageIndex{4}\) : Vecteur de position du proton à\(t = 2.0 \times 10^{−7}\,ms = 200\, ns\). La trajectoire du proton est montrée. L'angle par lequel le proton se déplace le long du cercle est de 5,712 rad, soit un peu moins d'un tour complet.

L'importance

Nous avons choisi la position initiale de la particule pour qu'elle se trouve sur l'axe X. C'était totalement arbitraire. Si une position de départ différente était donnée, nous aurions une position finale différente à t = 200 ns.

Mouvement circulaire non uniforme

Le mouvement circulaire ne doit pas nécessairement se faire à une vitesse constante. Une particule peut se déplacer en cercle et accélérer ou ralentir, montrant ainsi une accélération dans le sens du mouvement.

Dans un mouvement circulaire uniforme, la particule effectuant un mouvement circulaire a une vitesse constante et le cercle se trouve à un rayon fixe. Si la vitesse de la particule change également, nous introduisons une accélération supplémentaire dans la direction tangente au cercle. De telles accélérations se produisent à un point du sommet qui modifie sa vitesse de rotation, ou à tout autre rotor qui accélère. Dans Vecteurs de déplacement et de vitesse, nous avons montré que l'accélération centripète est la vitesse temporelle de changement de la direction du vecteur de vitesse. Si la vitesse de la particule change, elle a une accélération tangentielle qui est le taux de variation dans le temps de l'amplitude de la vitesse :

\[a_{T} = \frac{d |\vec{v}|}{dt} \ldotp \label{4.31}\]

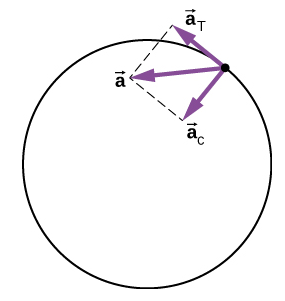
La direction de l'accélération tangentielle est tangente au cercle tandis que la direction de l'accélération centripète est radialement vers l'intérieur vers le centre du cercle. Ainsi, une particule en mouvement circulaire avec une accélération tangentielle a une accélération totale qui est la somme vectorielle des accélérations centripète et tangentielle :

\[\vec{a} = \vec{a}_{c} + \vec{a}_{T} \ldotp \label{4.32}\]

Les vecteurs d'accélération sont illustrés sur la figure\(\PageIndex{5}\). Notez que les deux vecteurs d'accélération\(\vec{a}_{c}\) et\(\vec{a}_{T}\) sont perpendiculaires l'un à l'autre,\(\vec{a}_{c}\) dans la direction radiale et\(\vec{a}_{T}\) dans la direction tangentielle. L'accélération totale se\(\vec{a}\) situe à un angle compris entre\(\vec{a}_{c}\) et\(\vec{a}_{T}\).

L'accélération d'une particule sur un cercle est représentée ainsi que ses composantes radiale et tangentielle. L'accélération centripète a sub c pointe radialement vers le centre du cercle. L'accélération tangentielle a sub T est tangente au cercle à la position de la particule. L'accélération totale est la somme vectorielle des accélérations tangentielle et centripète, qui sont perpendiculaires. — Figure\(\PageIndex{5}\) : L'accélération centripète pointe vers le centre du cercle. L'accélération tangentielle est tangente au cercle à la position de la particule. L'accélération totale est la somme vectorielle des accélérations tangentielle et centripète, qui sont perpendiculaires.

Exemple\(\PageIndex{3}\): Total Acceleration during Circular Motion

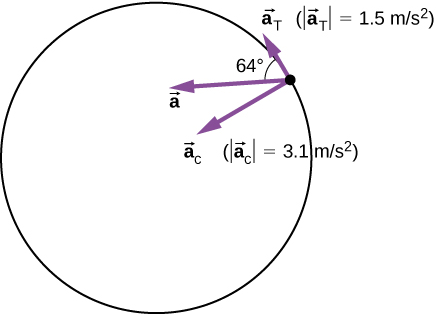
Une particule se déplace dans un cercle de rayon r = 2,0 m. Pendant l'intervalle de temps entre t = 1,5 s et t = 4,0 s, sa vitesse varie avec le temps selon

\[v(t) = c_{1} - \frac{c_{2}}{t^{2}}, c_{1} = 4.0\; m/s, c_{2} = 6.0\; m \cdotp s \ldotp\]

Quelle est l'accélération totale de la particule à t = 2,0 s ?

Stratégie

On nous donne la vitesse de la particule et le rayon du cercle, ce qui nous permet de calculer facilement l'accélération centripète. La direction de l'accélération centripète est dirigée vers le centre du cercle. Nous trouvons l'amplitude de l'accélération tangentielle en prenant la dérivée par rapport au temps de |v (t) | à l'aide de l'équation \ ref {4.31} et en l'évaluant à t = 2,0 s. Nous l'utilisons ainsi que l'amplitude de l'accélération centripète pour déterminer l'accélération totale.

Solution

L'accélération centripète est

\[v(2.0\; s) = \left(4.0 - \dfrac{6.0}{(2.0)^{2}}\right) m/s = 2.5\; m/s \nonumber \]

\[a_{c} = \frac{v^{2}}{r} = \frac{(2.5\; m/s)^{2}}{2.0\; m} = 3.1\; m/s^{2} \nonumber \]

dirigé vers le centre du cercle. L'accélération tangentielle est

\[a_{T} = \Big| \frac{d \vec{v}}{dt} \Big| = \frac{2 c_{2}}{t^{3}} = \frac{12.0}{(2.0)^{3}} m/s^{2} = 1.5\; m/s^{2} \ldotp \nonumber \]

L'accélération totale est

\[|\vec{a}| = \sqrt{3.1^{2} + 1.5^{2}} m/s^{2} = 3.44\; m/s^{2}\]

et\(\theta\) = tan ⁻¹\(\left(\dfrac{3.1}{1.5}\right)\) = 64° par rapport à la tangente au cercle. Voir la figure\(\PageIndex{6}\).

alt="L'accélération d'une particule sur un cercle est indiquée avec ses composantes radiale et tangentielle. L'accélération centripète a sub c pointe radialement vers le centre du cercle et a une magnitude de 3,1 mètres par seconde au carré. L'accélération tangentielle a sub T est tangente au cercle à la position de la particule et a une magnitude de 1,5 mètre par seconde au carré. L'angle entre l'accélération totale a et l'accélération tangentielle a sub T est de 64 degrés. » — Figure\(\PageIndex{6}\) : Les vecteurs d'accélération tangentielle et centripète. L'accélération nette\(\vec{a}\) est la somme vectorielle des deux accélérations.

L'importance

Les directions des accélérations centripètes et tangentielles peuvent être décrites plus facilement en termes de système de coordonnées polaires, avec des vecteurs unitaires dans les directions radiale et tangentielle. Ce système de coordonnées, qui est utilisé pour les déplacements le long de trajectoires courbes, est discuté en détail plus loin dans le livre.