4.4 : Mouvement du projectile

Last updated
Save as PDF

Page ID: 191539

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Utilisez un mouvement unidimensionnel dans des directions perpendiculaires pour analyser le mouvement du projectile.
Calculez la portée, le temps de vol et la hauteur maximale d'un projectile lancé qui entre en collision avec une surface plane et horizontale.
Déterminez l'heure de vol et la vitesse d'impact d'un projectile qui atterrit à une hauteur différente de celle du lancement.
Calculez la trajectoire d'un projectile.

Le mouvement du projectile est le mouvement d'un objet projeté ou projeté en l'air, soumis uniquement à une accélération due à la gravité. Les applications du mouvement des projectiles en physique et en ingénierie sont nombreuses. Parmi les exemples, citons les météores lorsqu'ils pénètrent dans l'atmosphère de la Terre, les feux d'artifice et le mouvement de n'importe quelle balle dans le sport. Ces objets sont appelés projectiles et leur trajectoire est appelée trajectoire. Le mouvement des objets qui tombent, tel que décrit dans Motion Along a Straight Line, est un type unidimensionnel simple de mouvement de projectile dans lequel il n'y a aucun mouvement horizontal. Dans cette section, nous examinons le mouvement bidimensionnel des projectiles, et notre traitement néglige les effets de la résistance à l'air.

Le fait le plus important à retenir ici est que les mouvements le long des axes perpendiculaires sont indépendants et peuvent donc être analysés séparément. Nous avons discuté de ce fait dans les vecteurs de déplacement et de vitesse, où nous avons vu que les mouvements verticaux et horizontaux sont indépendants. La clé pour analyser le mouvement bidimensionnel d'un projectile est de le diviser en deux mouvements : l'un le long de l'axe horizontal et l'autre le long de la verticale. (Ce choix d'axes est le plus judicieux car l'accélération résultant de la gravité est verticale ; il n'y a donc pas d'accélération le long de l'axe horizontal lorsque la résistance de l'air est négligeable.) Comme d'habitude, on appelle l'axe horizontal l'axe des abscisses et l'axe vertical l'axe des y. Il n'est pas obligatoire d'utiliser ce choix d'axes ; c'est simplement pratique dans le cas d'une accélération gravitationnelle. Dans d'autres cas, nous pouvons choisir un ensemble d'axes différent. La figure$\PageIndex{1}$ illustre la notation du déplacement, où nous définissons$\vec{s}$ comme étant le déplacement total,$\vec{x}$ et$\vec{y}$ ses vecteurs constitutifs le long des axes horizontal et vertical, respectivement. Les magnitudes de ces vecteurs sont s, x et y.

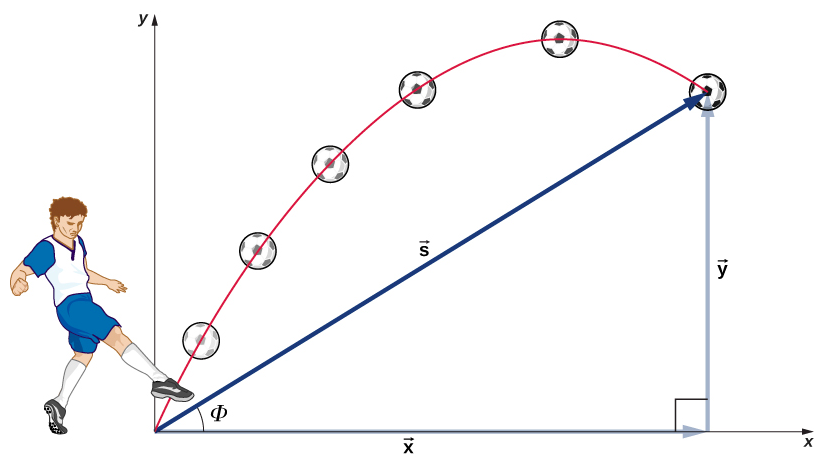
Illustration d'un joueur de football qui donne un coup de pied à un ballon. Le pied du joueur de football est à l'origine d'un système de coordonnées x y. La trajectoire du ballon de football et sa position à 6 instants sont affichées. La trajectoire est une parabole. Le vecteur s est le déplacement entre la position d'origine et la position finale du ballon de football. Le vecteur s et ses composantes x et y forment un triangle droit, avec s comme hypoténuse et un angle phi entre l'axe x et s. — Figure$\PageIndex{1}$ : Déplacement total s d'un ballon de football en un point sur sa trajectoire. Le vecteur$\vec{s}$ comporte des composantes$\vec{x}$ et$\vec{y}$ se trouve le long des axes horizontal et vertical. Sa magnitude est s et elle fait un angle$\phi$ avec l'horizontale.

Pour décrire complètement le mouvement du projectile, nous devons inclure la vitesse et l'accélération, ainsi que le déplacement. Nous devons trouver leurs composants le long des axes X et Y. Supposons que toutes les forces, à l'exception de la gravité (comme la résistance à l'air et le frottement, par exemple) soient négligeables. En définissant la direction positive vers le haut, les composantes de l'accélération sont alors très simples :

\[a_{y} = −g = −9.8\; m/s^{2} (− 32\; ft/s^{2}) \ldotp\]

Comme la gravité est verticale, a _x = 0. Si a _x = 0, cela signifie que la vitesse initiale dans la direction x est égale à la vitesse finale dans la direction x, ou v _x = v _0x. Avec ces conditions d'accélération et de vitesse, nous pouvons écrire les équations cinématiques 4.11 à 4.18 pour le mouvement dans un champ gravitationnel uniforme, y compris le reste des équations cinématiques pour une accélération constante à partir d'un mouvement à accélération constante. Les équations cinématiques du mouvement dans un champ gravitationnel uniforme deviennent des équations cinématiques avec a _y = −g, a _x = 0 :

Mouvement horizontal

\[v_{0x} = v_{x}, \quad x = x_{0} + v_{x} t \label{4.19}\]

Mouvement vertical

\[y = y_{0} + \frac{1}{2} (v_{0y} + v_{y})t \label{4.20}\]

\[v_{y} = v_{0y} - gt \label{4.21}\]

\[y = y_{0} + v_{0y} t - \frac{1}{2} g t^{2} \label{4.22}\]

\[v_{y}^{2}= v_{0y}^{2} + 2g(y − y_{0}) \label{4.23}\]

À l'aide de cet ensemble d'équations, nous pouvons analyser le mouvement des projectiles en gardant à l'esprit certains points importants.

Stratégie de résolution de problèmes : mouvement du projectile

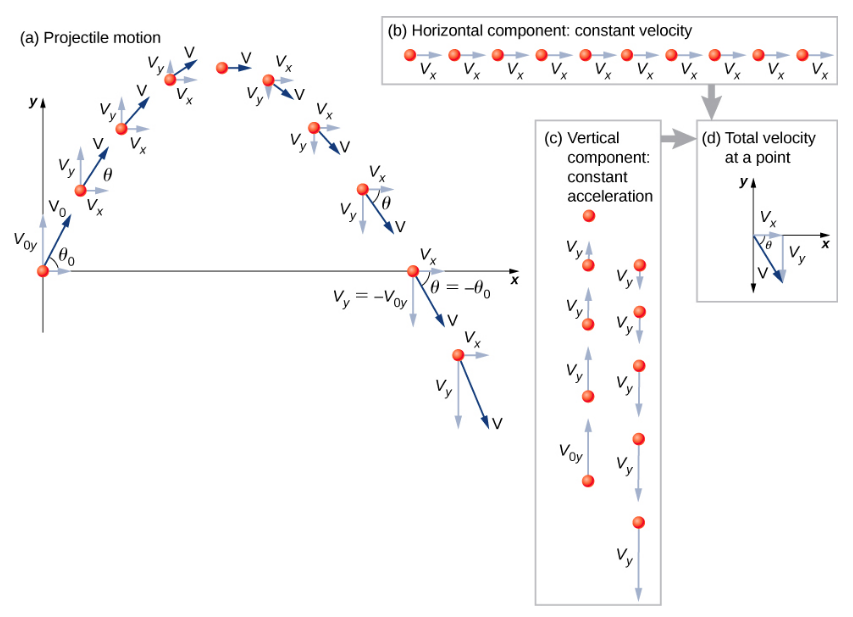
Répartissez le mouvement en composantes horizontales et verticales le long des axes X et Y. Les magnitudes des composantes du déplacement$\vec{s}$ le long de ces axes sont x et y. Les magnitudes des composantes de la vitesse$\vec{v}$ sont v _x = vcos$\theta$ et v _y = vsin$\theta$, où v est l'amplitude de la vitesse et$\theta$ sa direction par rapport à l'horizontale, comme le montre la figure$\PageIndex{2}$.
Traitez le mouvement comme deux mouvements unidimensionnels indépendants : l'un horizontal et l'autre vertical. Utilisez les équations cinématiques pour les mouvements horizontaux et verticaux présentées précédemment.
Résolvez les inconnues en effectuant deux mouvements distincts : l'un horizontal et l'autre vertical. Notez que la seule variable commune entre les mouvements est le temps t. Les procédures de résolution de problèmes ici sont les mêmes que celles de la cinématique unidimensionnelle et sont illustrées dans les exemples résolus suivants.
Recombinez les quantités dans les directions horizontale et verticale pour trouver le déplacement total$\vec{s}$ et la vitesse$\vec{v}$. Déterminez l'amplitude et la direction du déplacement et de la vitesse en utilisant $$s = \ sqrt {x^ {2} + y^ {2}} \ ldotp \ quad \ phi = \ tan^ {-1} \ left (\ dfrac {y} {x} \ right), \ quad v = \ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} \ ldort {x} ^ {2} tp$$where$\phi$ est la direction du déplacement$\vec{s}$.

La figure a montre les positions et les vitesses d'un projectile sur un système de coordonnées x y à 10 instants. Lorsque le projectile est à l'origine, il a une vitesse v sub 0 y qui fait un angle theta sub 0 avec l'horizontale. La vitesse est représentée par une flèche bleu foncé, et ses composantes x et y sont représentées par une flèche bleu clair. La position du projectile suit une parabole s'ouvrant vers le bas, se déplaçant jusqu'à une hauteur maximale, puis revenant à y = 0, et continuant sous l'axe des x. La vitesse, V, forme à chaque fois un angle thêta qui change dans le temps, et a une composante x V sub x et une composante y v sub y. La composante x de la vitesse V sub x est toujours le même. La composante y v sub y pointe vers le haut mais diminue, jusqu'à ce que le projectile atteigne la hauteur maximale, où la vitesse est horizontale et ne comporte pas de composante y. Après la hauteur maximale, la composante y de la vitesse est dirigée vers le bas et augmente. Lorsque le projectile atteint la même altitude en descendant qu'en montant, sa vitesse est inférieure à l'horizontale selon le même angle thêta qu'il était au-dessus de l'horizontale en montant. En particulier, lorsqu'on revient à y = 0 en descendant, l'angle entre le vecteur v et l'horizontale est de moins s=theta sous zéro et la composante y de la vitesse est moins v sub 0 y. La dernière position indiquée se trouve sous l'axe x, et la composante y de la vitesse est plus grande qu'elle ne l'était initialement. Le graphique montre clairement que les distances horizontales parcourues dans chacun des intervalles de temps sont égales, tandis que les distances verticales diminuent en montant et augmentent en descendant. La figure b montre la composante horizontale, vitesse constante. Les positions horizontales et les composantes x de la vitesse du projectile sont indiquées le long d'une ligne horizontale. Les positions sont régulièrement espacées et les composantes x des vitesses sont toutes identiques et pointent vers la droite. La figure c montre la composante verticale, accélération constante. Les positions verticales et les composantes y de la vitesse du projectile sont indiquées le long d'une ligne verticale. Les positions se rapprochent en montant, puis s'éloignent en descendant. Les composantes y des vitesses pointent initialement vers le haut et diminuent en amplitude jusqu'à ce qu'il n'y ait plus de composante y de la vitesse à la hauteur maximale. Après la hauteur maximale, les composantes y des vitesses pointent vers le bas et augmentent en amplitude. La figure d montre que la combinaison des composantes horizontale et verticale des figures b et c donne la vitesse totale en un point. La vitesse V possède une composante x de V sub x, une composante y de V sub y et forme un angle thêta avec l'horizontale. Dans l'exemple illustré, la vitesse a une composante y descendante. — Figure$\PageIndex{2}$ : (a) Nous analysons le mouvement bidimensionnel du projectile en le divisant en deux mouvements unidimensionnels indépendants le long des axes vertical et horizontal. (b) Le mouvement horizontal est simple, car a _x = 0 et v _x est une constante. (c) La vitesse dans le sens vertical commence à diminuer à mesure que l'objet s'élève. À son point le plus élevé, la vitesse verticale est nulle. Lorsque l'objet retombe vers la Terre, la vitesse verticale augmente à nouveau en amplitude mais pointe dans la direction opposée à la vitesse verticale initiale. (d) Les mouvements x et y sont recombinés pour donner la vitesse totale à un point donné de la trajectoire.

Exemple 4.7 : Un projectile de feu d'artifice explose haut et loin

Lors d'un feu d'artifice, un obus est projeté en l'air à une vitesse initiale de 70,0 m/s à un angle de 75,0° au-dessus de l'horizontale, comme illustré sur la figure$\PageIndex{3}$. Le fusible est programmé pour allumer la coque au moment où elle atteint son point le plus élevé au-dessus du sol. a) Calculez la hauteur à laquelle l'obus explose. b) Combien de temps s'écoule entre le lancement de l'obus et l'explosion ? (c) Quel est le déplacement horizontal de l'obus lorsqu'il explose ? d) Quel est le déplacement total entre le point de lancement et le point le plus haut ?

La trajectoire d'un obus de feu d'artifice depuis son lancement jusqu'à son point le plus haut est représentée par la moitié gauche d'une parabole s'ouvrant vers le bas sur un graphique représentant y en fonction de x. La hauteur maximale est h = 233 mètres et son déplacement x à ce moment-là est x = 125 mètres. Le vecteur de vitesse initial v sub 0 est situé vers le haut et vers la droite, tangent à la courbe de trajectoire, et forme un angle de thêta sub 0 égal à 75 degrés. — Figure$\PageIndex{3}$ : Trajectoire d'un obus de feu d'artifice. Le dispositif de mise à feu est réglé pour faire exploser l'obus au point le plus élevé de sa trajectoire, qui se trouve à 233 m de hauteur et à 125 m de distance à l'horizontale.

Stratégie

Le mouvement peut être divisé en mouvements horizontaux et verticaux dans lesquels a _x = 0 et a _y = −g. Nous pouvons ensuite définir x ₀ et y ₀ comme nuls et résoudre les quantités souhaitées.

Solution

Par « hauteur », nous entendons l'altitude ou la position verticale y au-dessus du point de départ. Le point le plus élevé de toute trajectoire, appelé sommet, est atteint lorsque v _y = 0. Puisque nous connaissons les vitesses initiale et finale, ainsi que la position initiale, nous utilisons l'équation suivante pour trouver y : $$v_ {y} ^ {2} = v_ {0y} ^ {2} - 2g (y - y_ {0}) \ LDotp$$Parce que y 0 et v y sont tous deux nuls, l'équation se simplifie à 0$ = v_ {0y} ^ {2} - 2$ Parce que _{y ₀ et v y} sont tous deux nuls, l'équation se simplifie à 0$ = v_ {0y} ^ {2} - 2$ gy \ lDotp$$Résoudre pour y donne $$y = \ frac {v_ {0y} ^ {2}} {2g} \ LDotp$$Nous devons maintenant trouver v _0y, la composante de la vitesse initiale dans la direction y. Il est donné par v _0y = v ₀ sin$\theta_{0}$, où v ₀ est la vitesse initiale de 70,0 m/s et$\theta_{0}$ = 75° est l'angle initial. Ainsi $$v_ {0y} = v_ {0} \ sin \ theta = (70,0 \ ; m/s) \ sin 75^ {o} = 67,6 \ ; m/s$$et y est $$y = \ frac {(67,6 \ ; m/s) ^ {2}} {2}} {2 \ ; m/s^ {2})} \ LDotp$$Ainsi, nous avons $$y = 233 \ ; m \ LDotp$$Notez que, comme le haut est positif, la vitesse verticale initiale est positive, tout comme la hauteur maximale, mais l'accélération qui en résulte de la gravité est négative. Notez également que la hauteur maximale dépend uniquement de la composante verticale de la vitesse initiale, de sorte que tout projectile ayant une composante verticale initiale de vitesse de 67,6 m/s atteint une hauteur maximale de 233 m (en négligeant la résistance de l'air). Dans cet exemple, les chiffres sont raisonnables pour les grands feux d'artifice, dont les obus atteignent de telles hauteurs avant d'exploser. En pratique, la résistance de l'air n'est pas totalement négligeable, de sorte que la vitesse initiale devrait être légèrement supérieure à celle donnée pour atteindre la même hauteur.
Comme dans de nombreux problèmes de physique, il existe plusieurs manières de résoudre le problème lorsque le projectile atteint son point le plus élevé. Dans ce cas, la méthode la plus simple consiste à utiliser v _y = v _0y − gt. Comme v _y = 0 au sommet, cette équation réduit 0$ = v_ {0y} - gt$$or $$t = \ frac {v_ {0y}} {g} = \ frac {67,6 \ ; m/s} {9,80 \ ; m/s^ {2}} = 6,90 \ ; s \ LDotp$$Ce temps est également raisonnable pour les grands feux d'artifice. Si vous pouvez voir le lancement de feux d'artifice, remarquez que plusieurs secondes s'écoulent avant que l'obus n'explose. Une autre façon de déterminer l'heure est d'utiliser y = y ₀ +$\frac{1}{2}$ (v _0y _{+ v y}) t. Cet exercice vous est laissé à compléter.
Comme la résistance de l'air est négligeable, a _x = 0 et la vitesse horizontale est constante, comme indiqué précédemment. Le déplacement horizontal est la vitesse horizontale multipliée par le temps, comme indiqué par x = x ₀ + v _x t, où x ₀ est égal à zéro. Ainsi, $$x = v_ {x} t, $$où v _x est la composante x de la vitesse, qui est donnée par $$v_ {x} = v_ {0} \ cos \ theta = (70,0 \ ; m/s) \ cos 75^ {o} = 18,1 \ ; m/s \ LDotp$$Le temps t pour les deux mouvements est le même, donc x est $$x = (18,1 \ ; m/s) (6,90 \ ; s) = 125 \ ; m \ LDotp$$Le mouvement horizontal est une vitesse constante dans absence de résistance à l'air. Le déplacement horizontal trouvé ici pourrait être utile pour empêcher les fragments de feux d'artifice de tomber sur les spectateurs. Lorsque l'obus explose, la résistance de l'air a un effet majeur et de nombreux fragments tombent directement en dessous.
Les composantes horizontale et verticale du déplacement viennent d'être calculées, il suffit donc de trouver l'amplitude et la direction du déplacement au point le plus élevé : $$ \ vec {s} = 125 \ hat {i} + 233 \ hat {j} $$$| \ vec {s} | = \ sqrt {125^ {2} + 233 ^ {2}} = 264 \ ; m$$$ \ thêta = \ tan^ {-1} \ left (\ dfrac { 233} {125} \ right) = 61,8^ {o} \ LDotp$$Notez que l'angle du vecteur de déplacement est inférieur à l'angle initial de lancement. Pour comprendre pourquoi, consultez la figure$\PageIndex{1}$, qui montre la courbure de la trajectoire vers le niveau du sol. Lors de la résolution de l'exemple 4.7 (a), l'expression que nous avons trouvée pour y est valide pour tout mouvement de projectile lorsque la résistance de l'air est négligeable. Appelez la hauteur maximale y = h. Ensuite, $$h = \ frac {v_ {0y} ^ {2}} {2g} \ LDotp$$Cette équation définit la hauteur maximale d'un projectile au-dessus de sa position de lancement et dépend uniquement de la composante verticale de la vitesse initiale.

Exercice 4.3

Une pierre est projetée horizontalement depuis une falaise de 100,0 m de haut à une vitesse de 15,0 m/s. (a) Définissez l'origine du système de coordonnées. (b) Quelle équation décrit le mouvement horizontal ? (c) Quelles équations décrivent le mouvement vertical ? (d) Quelle est la vitesse de la roche au point d'impact ?

Exemple 4.8 : Calcul du mouvement d'un projectile - Joueur de tennis

Un joueur de tennis gagne un match au stade Arthur Ashe et frappe une balle dans les gradins à 30 m/s et à un angle de 45° au-dessus de l'horizontale (Figure$\PageIndex{4}$). En descendant, la balle est rattrapée par un spectateur à 10 m au-dessus du point où elle a été touchée. (a) Calculez le temps qu'il faut à la balle de tennis pour atteindre le spectateur. (b) Quelles sont l'amplitude et la direction de la vitesse de la balle au moment de l'impact ?

Illustration d'une balle de tennis lancée dans les gradins. Le joueur se trouve à gauche des gradins et frappe la balle vers le haut et vers la droite avec un angle de thêta égal à 45 degrés et une vitesse de v sub 0 égale à 30 mètres par seconde. Le ballon atteint un spectateur assis à 10 mètres au-dessus de la hauteur initiale du ballon. — Figure$\PageIndex{4}$ : Trajectoire d'une balle de tennis frappée dans les gradins.

Stratégie

Encore une fois, la résolution de ce mouvement bidimensionnel en deux mouvements unidimensionnels indépendants nous permet de résoudre les quantités souhaitées. Le temps pendant lequel un projectile est en l'air dépend uniquement de son mouvement vertical. Ainsi, nous le résolvons d'abord. Lorsque la balle monte et descend verticalement, le mouvement horizontal se poursuit à une vitesse constante. Cet exemple demande la vitesse finale. Ainsi, nous recombinons les résultats verticaux et horizontaux pour obtenir$\vec{v}$ à l'instant final t, déterminé dans la première partie de l'exemple.

Solution

Lorsque la balle est en l'air, elle monte puis descend jusqu'à une position finale supérieure de 10,0 m à son altitude de départ. Nous pouvons trouver le temps pour cela en utilisant l'équation \ ref {4.22} : $$y = y_ {0} + v_ {0y} t - \ frac {1} {2} gt^ {2} \ LDotp$$Si nous prenons la position initiale y ₀ nulle, alors la position finale est y = 10 m. La vitesse verticale initiale est la composante verticale de la vitesse initiale : $$v_ {0} = v_ {0} \ sin \ theta_ {0} = (30,0 \ ; m/s) \ sin 45^ {o} = 21,2 \ ; m/s \ LDotp$$La substitution de y dans l'équation \ ref {4.22} nous donne 10,0$ \ ; m = (21,2 \ ; m/s) t − (4,90 \ ; m/s^ {2}) t^ {2}) t^ {2} \ LDotp$$La réorganisation des termes donne une équation quadratique t : $$ (4,90 \ ; m/s^ {2}) t^ {2} − (21,2 \ ; m/s) t + 10,0 \ ; m = 0 \ LDotp$$Utilisation de la formule quadratique donne t = 3,79 s et t = 0,54 s. Comme la balle se trouve à une hauteur de 10 m à deux reprises au cours de sa trajectoire, une fois en montée et une fois en descente, nous prenons la solution la plus longue pour le temps qu'il faut à la balle pour atteindre le spectateur : $$t = 3,79 \ ; s \ LDotp$$Le temps de mouvement du projectile est complètement déterminé par le mouvement vertical. Ainsi, tout projectile qui a une vitesse verticale initiale de 21,2 m/s et atterrit à 10,0 m au-dessus de son altitude de départ passe 3,79 s dans les airs.
Nous pouvons déterminer les vitesses horizontales et verticales finales v _x et v _y en utilisant le résultat de (a). Ensuite, nous pouvons les combiner pour déterminer l'amplitude du vecteur de vitesse totale$\vec{v}$ et l'angle$\theta$ qu'il fait avec l'horizontale. Puisque v _x est constant, nous pouvons le résoudre à n'importe quel endroit horizontal. Nous choisissons le point de départ car nous connaissons à la fois la vitesse initiale et l'angle initial. Par conséquent, $$v_ {x} = v_ {0} \ cos \ theta_ {0} = (30 \ ; m/s) \ cos 45^ {o} = 21,2 \ ; m/s \ LDotp$$La vitesse verticale finale est donnée par l'équation \ ref {4.21} : $$v_ {y} = v_ {0y} − gt \ LDotp$$since$v_{0y}$ a été trouvé dans la partie (a) soit 21,2 m/s, nous avons $$v_ {y} = 21,2 \ ; m/s − (9,8 \ ; m/s^ {2}) (3,79 s) = −15,9 \ ; m/s \ ldotp$$ L'amplitude de la vitesse finale$\vec{v}$ est $$v = \ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} = \ sqrt {(21,2 \ ; m/s) ^ {2} + (-15,9 \ ; m/s) ^ {2}} = 26,5 \ ; m/s \ LDotp$$La direction$\theta_{v}$ est trouvée en utilisant la tangente inverse : $$ \ theta_ {v} = \ tan^ {-1} \ left (\ dfrac {v_ {y}}} {v_ {x}} \ right) = \ tan^ {-1} \ left (\ dfrac {21,2} {-15,9}} \ (droite) = -53.1^ {o} \ ldotp$$

L'importance

Comme indiqué précédemment, le temps de mouvement du projectile est entièrement déterminé par le mouvement vertical. Ainsi, tout projectile qui a une vitesse verticale initiale de 21,2 m/s et atterrit à 10,0 m au-dessus de son altitude de départ passe 3,79 s dans les airs.
L'angle négatif signifie que la vitesse est de 53,1 degrés en dessous de l'horizontale au point d'impact. Ce résultat est cohérent avec le fait que la balle impacte un point situé de l'autre côté du sommet de la trajectoire et possède donc une composante y négative de la vitesse. L'amplitude de la vitesse est inférieure à l'amplitude de la vitesse initiale attendue puisqu'elle a un impact à 10,0 m au-dessus de l'altitude de lancement.

Heure de vol, trajectoire et distance

Le temps de vol, la trajectoire et la portée d'un projectile lancé sur une surface plane horizontale et percutant la même surface sont intéressants. Dans ce cas, les équations cinématiques fournissent des expressions utiles pour ces quantités, qui sont dérivées dans les sections suivantes.

Heure du vol

Nous pouvons résoudre le temps de vol d'un projectile qui est à la fois lancé et impacté sur une surface plane horizontale en effectuant quelques manipulations des équations cinématiques. Nous remarquons que la position et le déplacement en y doivent être nuls au lancement et à l'impact sur une surface plane. Ainsi, nous définissons le déplacement en y égal à zéro et trouvons

\[y − y_{0} = v_{0y} t − \frac{1}{2} gt^{2} = (v_{0} \sin \theta_{0})t − \frac{1}{2} gt^{2} = 0 \ldotp\]

Affacturage, nous avons

\[t \left(v_{0} \sin \theta_{0} - \dfrac{gt}{2}\right) = 0 \ldotp\]

Résoudre cela nous donne

\[T_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

C'est le temps de vol d'un projectile lancé et percutant une surface plane et horizontale. L'équation \ ref {4.24} ne s'applique pas lorsque le projectile atterrit à une altitude différente de celle à laquelle il a été lancé, comme nous l'avons vu dans l'exemple 4.8 où un joueur de tennis frappe la balle dans les gradins. L'autre solution, t = 0, correspond à l'heure du lancement. Le temps de vol est linéairement proportionnel à la vitesse initiale dans la direction y et inversement proportionnel à g. Ainsi, sur la Lune, où la gravité est un sixième de celle de la Terre, un projectile lancé à la même vitesse que sur Terre serait aéroporté six fois plus longtemps.

Trajet

La trajectoire d'un projectile peut être déterminée en éliminant la variable temporelle t des équations cinématiques pour t arbitraire et en résolvant pour y (x). On prend x ₀ = y ₀ = 0 pour que le projectile soit lancé depuis l'origine. L'équation cinématique pour x donne

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0}} \ldotp\]

En substituant l'expression de t dans l'équation de la position y = (v ₀ sin$\theta_{0}$) t −$\frac{1}{2}$ gt ², on obtient

\[y = (v_{0} \sin \theta_{0}) \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right) - \frac{1}{2} g \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right)^{2} \ldotp\]

Réorganisation des termes, nous avons

\[y = (\tan \theta_{0})x - \Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big] x^{2} \ldotp \label{4.25}\]

Cette équation de trajectoire est de la forme y = ax + bx ², qui est une équation d'une parabole à coefficients

\[a = \tan \theta_{0}, \quad b = - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \ldotp\]

Gamme

À partir de l'équation de trajectoire, nous pouvons également déterminer la distance horizontale parcourue par le projectile. Équation de factorisation \ ref {4.25}, nous avons

\[y = x \Big[ \tan \theta_{0} - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} x \Big] \ldotp\]

La position y est nulle à la fois pour le point de lancement et pour le point d'impact, car nous ne considérons à nouveau qu'une surface horizontale plane. La valeur y = 0 dans cette équation donne des solutions x = 0, correspondant au point de lancement, et

\[x = \frac{2 v_{0}^{2} \sin \theta_{0} \cos \theta_{0}}{g} ,\]

correspondant au point d'impact. En utilisant l'identité trigonométrique 2sin$\theta$ cos$\theta$ = sin2$\theta$ et en réglant x = R pour la plage, nous trouvons

\[R = \frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \ldotp \label{4.26}\]

Notez en particulier que l'équation \ ref {4.26} n'est valable que pour le lancement et l'impact sur une surface horizontale. Nous voyons que la plage est directement proportionnelle au carré des vitesses initiales v ₀ et sin ²$\theta_{0}$, et qu'elle est inversement proportionnelle à l'accélération de la gravité. Ainsi, sur la Lune, la portée serait six fois plus grande que sur Terre pour la même vitesse initiale. De plus, on voit à partir du facteur sin ²$\theta_{0}$ que la plage est maximale à 45°. Ces résultats sont présentés dans la figure$\PageIndex{5}$. Dans (a), nous voyons que plus la vitesse initiale est élevée, plus la plage est grande. En (b), on voit que la plage est maximale à 45°. Cela n'est vrai que pour les conditions qui négligent la résistance à l'air. Si la résistance de l'air est prise en compte, l'angle maximum est légèrement plus petit. Il est intéressant de noter que la même portée est trouvée pour deux angles de lancement initiaux dont la somme est de 90°. Le projectile lancé avec l'angle le plus petit a un sommet plus bas que l'angle supérieur, mais les deux ont la même portée.

La figure a montre les trajectoires des projectiles lancés au même angle initial de 45 degrés au-dessus de l'horizontale et à différentes vitesses initiales. Les trajectoires sont affichées du lancement à l'atterrissage à l'altitude initiale. En orange, la trajectoire sur 30 mètres par seconde, soit une portée R (distance entre le lancement et l'atterrissage) de 91,8 m. En violet, la trajectoire sur 40 mètres par seconde, soit une portée R de 163 m. En bleu, la trajectoire sur 50 mètres par seconde, soit une portée R de 255 m. La hauteur maximale du projectile augmente avec la vitesse initiale. La figure b montre les trajectoires des projectiles lancés à la même vitesse initiale de 50 mètres par seconde et à différents angles de lancement. Les trajectoires sont affichées du lancement à l'atterrissage à l'altitude initiale. En orange est la trajectoire pour un angle de 15 degrés au-dessus de l'horizontale, ce qui donne une portée R de 128 m. En violet est la trajectoire pour un angle de 45 degrés au-dessus de l'horizontale, soit une distance R de 255 m. En bleu est la trajectoire pour un angle de 75 degrés au-dessus de l'horizontale, donnant une portée R de 128 m, comme pour la trajectoire à 15 degrés. La hauteur maximale augmente avec l'angle de lancement. — Figure$\PageIndex{5}$ : Trajectoires des projectiles sur un sol plat. (a) Plus la vitesse initiale v ₀ est élevée, plus la plage pour un angle initial donné est grande. (b) L'effet de l'angle initial (\ theta_ {0} \) sur la portée d'un projectile à une vitesse initiale donnée. Notez que la plage est la même pour les angles initiaux de 15° et 75°, bien que les hauteurs maximales de ces trajectoires soient différentes.

Exemple 4.9 : Comparaison de coups de golf

Un golfeur se retrouve dans deux situations différentes sur des trous différents. Sur le deuxième trou, il se trouve à 120 m du green et veut frapper la balle à 90 m et la laisser courir sur le green. Il oriente le tir bas par rapport au sol à 30° par rapport à l'horizontale pour laisser la balle rouler après l'impact. Sur le quatrième trou, il se trouve à 90 m du green et veut laisser tomber la balle avec un minimum de roulis après l'impact. Ici, il oriente le tir à 70° par rapport à l'horizontale afin de minimiser le roulement après l'impact. Les deux tirs sont touchés et impactés sur une surface plane. (a) Quelle est la vitesse initiale de la balle au deuxième trou ? (b) Quelle est la vitesse initiale de la balle au quatrième trou ? (c) Écrivez l'équation de trajectoire pour les deux cas. (d) Représenter graphiquement les trajectoires.

Stratégie

Nous voyons que l'équation de plage contient la vitesse et l'angle initiaux, de sorte que nous pouvons résoudre la vitesse initiale pour (a) et (b). Lorsque nous avons la vitesse initiale, nous pouvons utiliser cette valeur pour écrire l'équation de trajectoire.

Solution

$$R = \ frac {v_ {0} ^ {2} \ sin 2 \ theta_ {0}} {g} \ Flèche droite v_ {0} = \ sqrt {\ dfrac {Rg} {\ sin 2 \ theta_ {0}}} = \ sqrt {\ dfrac {(90,0 \ ; m) (9,8 \ ; m/s^ {2})} {\ sin (2 (30^ {o}))}} = 31,9 \ ; m/s$$
$$R = \ frac {v_ {0} ^ {2} \ sin 2 \ theta_ {0}} {g} \ Flèche droite v_ {0} = \ sqrt {\ dfrac {Rg} {\ sin 2 \ theta_ {0}}} = \ sqrt {\ dfrac {(90,0 \ ; m) (9,8 \ ; m/s^ {2})} {\ sin (2 (70^ {o}))}} = 37,0 \ ; m/s$$
$$y = x \ Big [\ tan \ theta_ {0} - \ frac {g} {2 (v_ {0} \ cos \ theta_ {0}) ^ {2}} x \ Big] $$Deuxième trou : $$y = x \ Big [\ tan 30^ {o} - \ frac {9.8 \ ; m/s^ {2}} {2}} {2 [(31,9 \ ; m/s) (\ cos 30^ {o})] ^ {2}} x \ Big] = 0,58x - 0,0064x^ {2} $Quatrième trou : $$y = x \ Big [\ tan 70^ {o} - \ frac {9,8 \ ; m/s^ {2}} {2}} {2} {2}} {2}} {2}} {2}} {2}} x \ Grand] = 2 0,75 x - 0,0306 x ^ {2} $
À l'aide d'un utilitaire graphique, nous pouvons comparer les deux trajectoires, qui sont illustrées sur la figure$\PageIndex{6}$.

Deux fonctions paraboliques sont affichées. La portée des deux trajectoires est de 90 mètres. Un tir se déplace beaucoup plus haut que l'autre. Le tir le plus haut a une vitesse initiale de 37 mètres par seconde et un angle de 70 degrés. Le tir le plus bas a une vitesse initiale de 31,9 mètres par seconde et un angle de 30 degrés. — Figure$\PageIndex{6}$ : Deux trajectoires d'une balle de golf d'une portée de 90 m. Les points d'impact des deux se situent au même niveau que le point de lancement.

L'importance

La vitesse initiale du tir à 70° est supérieure à la vitesse initiale du tir à 30°. Notez sur la figure$\PageIndex{6}$ que deux projectiles lancés à la même vitesse mais sous des angles différents ont la même portée si les angles de lancement s'ajoutent à 90°. Dans cet exemple, les angles de lancement s'additionnent pour donner un nombre supérieur à 90°. Ainsi, le tir à 70° doit avoir une vitesse de lancement plus élevée pour atteindre 90 m, sinon il atterrirait à une distance plus courte.

Exercice 4.4

Si les deux coups de golf de l'exemple 4.9 étaient lancés à la même vitesse, lequel aurait la plus grande portée ?

Lorsque nous parlons de la portée d'un projectile sur un sol plat, nous supposons que R est très petit par rapport à la circonférence de la Terre. Toutefois, si la portée est grande, la Terre s'éloigne en dessous du projectile et l'accélération résultant de la gravité change de direction le long de la trajectoire. La portée est plus grande que celle prédite par l'équation de distance donnée précédemment, car le projectile doit tomber plus loin qu'il ne le ferait sur un sol plat, comme le montre la figure$\PageIndex{7}$, qui est basée sur un dessin du Principia de Newton. Si la vitesse initiale est suffisante, le projectile se met en orbite. La surface de la Terre chute de 5 m tous les 8 000 m. En 1 seconde, un objet tombe de 5 m sans résistance à l'air. Ainsi, si un objet reçoit une vitesse horizontale de 8 000 m/s (ou 18 000 mi/h) près de la surface de la Terre, il se mettra en orbite autour de la planète car la surface s'éloigne continuellement de l'objet. Il s'agit à peu près de la vitesse de la navette spatiale sur une orbite terrestre basse lorsqu'elle était opérationnelle, ou de tout satellite sur une orbite terrestre basse. Ces aspects ainsi que d'autres aspects du mouvement orbital, tels que la rotation de la Terre, sont abordés plus en profondeur dans Gravitation.

La figure montre un dessin de la Terre avec une haute tour au pôle nord et une flèche horizontale étiquetée v 0 pointant vers la droite. 5 trajectoires commençant au sommet de la tour sont présentées. Le premier atteint la terre près de la tour. Le second atteint la terre plus loin de la tour, et le troisième encore plus loin. La quatrième trajectoire touche la Terre à l'équateur et est tangente à la surface de l'équateur. La cinquième trajectoire est un cercle concentrique à la Terre. — Figure$\PageIndex{7}$ : Projectile dirigé vers un satellite. Dans chaque cas illustré ici, un projectile est lancé depuis une tour très haute pour éviter la résistance de l'air. À mesure que la vitesse initiale augmente, la portée augmente et devient plus longue qu'elle ne le serait sur un sol plat, car la Terre se courbe en dessous de sa trajectoire. Avec une vitesse de 8000 m/s, l'orbite est atteinte.

Simulation

Sur PhET Explorations : Projectile Motion, découvrez le mouvement des projectiles en termes d'angle de lancement et de vitesse initiale.