Skip to main content
Global

6.3 : Expliquer la loi de Gauss

  1. Last updated
  2. Save as PDF
  • Page ID
    191105

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Loi de Gauss de l'État
    • Expliquer les conditions dans lesquelles la loi de Gauss peut être utilisée
    • Appliquer la loi de Gauss dans les systèmes appropriés

    Nous pouvons maintenant déterminer le flux électrique à travers une surface fermée arbitraire en raison d'une distribution de charge arbitraire. Nous avons découvert que si une surface fermée n'a aucune charge à l'intérieur de laquelle une ligne de champ électrique peut se terminer, toute ligne de champ électrique pénétrant dans la surface à un point doit nécessairement sortir à un autre point de la surface. Par conséquent, si une surface fermée ne contient aucune charge à l'intérieur du volume clos, le flux électrique à travers la surface est nul. Maintenant, qu'advient-il du flux électrique s'il y a des charges à l'intérieur du volume clos ? La loi de Gauss apporte une réponse quantitative à cette question.

    Pour avoir une idée de ce à quoi nous attendre, calculons le flux électrique à travers une surface sphérique autour d'une charge ponctuelle positive\(q\), car nous connaissons déjà le champ électrique dans une telle situation. Rappelons que lorsque nous plaçons la charge ponctuelle à l'origine d'un système de coordonnées, le champ électrique en un point\(P\)\(r\) éloigné de la charge à l'origine est donné par

    \[\vec{E}_p = \dfrac{1}{4\pi \epsilon_0}\dfrac{q}{r^2}\hat{r},\]

    où\(\hat{r}\) est le vecteur radial de la charge à l'origine au point P. Nous pouvons utiliser ce champ électrique pour trouver le flux à travers la surface sphérique de rayon r, comme indiqué sur la figure\(\PageIndex{1}\).

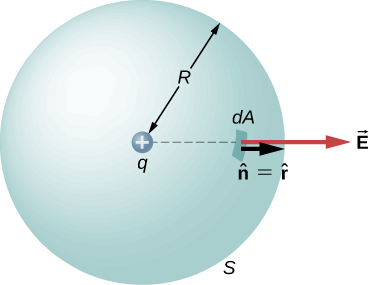
    Une sphère étiquetée S avec un rayon R est représentée. En son centre se trouve un petit cercle avec un signe plus, intitulé q. Une petite zone sur la sphère est étiquetée dA. À partir de là, deux flèches pointent vers l'extérieur, perpendiculairement à la surface de la sphère. La plus petite flèche est étiquetée en lettres égales ou égales à. La flèche la plus longue est étiquetée vecteur E.
    Figure\(\PageIndex{1}\) : Surface sphérique fermée entourant une charge ponctuelle q.

    Ensuite, nous appliquons\(\Phi = \int_S \vec{E} \cdot \hat{n} dA\) à ce système et y substituons des valeurs connues. Sur la sphère,\(\hat{n}\)\(r = R\) donc pour une aire infinitésimale dA,

    \[\begin{align*} d\Phi &= \vec{E} \cdot \hat{n} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \hat{r} \cdot \hat{r} dA \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} dA. \end{align*}\]

    Nous trouvons maintenant le flux net en intégrant ce flux sur la surface de la sphère :

    \[\Phi = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} \oint_S dA = \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{R^2} (4\pi R^2) = \dfrac{q}{\epsilon_0}.\]

    où la surface totale de la surface sphérique est\(4\pi R^2\). Cela donne le flux à travers la surface sphérique fermée avec un rayon\(r\) de

    \[\Phi = \dfrac{q}{\epsilon_0}.\]

    Un fait remarquable à propos de cette équation est que le flux est indépendant de la taille de la surface sphérique. Cela peut être directement attribué au fait que le champ électrique d'une charge ponctuelle diminue au fur et\(1/r^2\) à mesure de la distance, ce qui annule simplement le\(r^2\) taux d'augmentation de la surface.

    Image des lignes de champ électriques

    Une autre façon de comprendre pourquoi le flux à travers une surface sphérique fermée est indépendant du rayon de la surface consiste à examiner les lignes de champ électrique. Notez que chaque ligne de champ partant de q qui perce la surface selon un rayon perce\(R_1\) également la surface à\(R_2\) (Figure\(\PageIndex{2}\)).

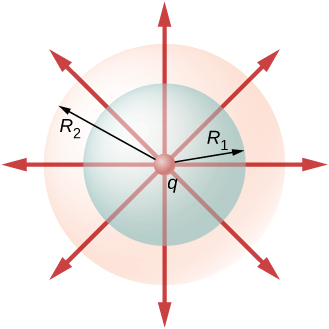
    La figure montre trois cercles concentriques. La plus petite au centre est nommée q, celle du milieu a le rayon R1 et la plus grande a le rayon R2. Huit flèches rayonnent vers l'extérieur à partir du centre dans les huit directions.
    Figure\(\PageIndex{2}\) : Les flux à travers des surfaces sphériques de\(R_2\) rayons\(R_1\) et entourant une charge q sont égaux, indépendamment de la taille de la surface, puisque toutes les lignes de champ E qui percent une surface de l'intérieur vers l'extérieur percent également l'autre surface dans le dans la même direction.

    Par conséquent, le nombre net de lignes de champ électrique traversant les deux surfaces de l'intérieur vers l'extérieur est égal. Ce nombre net de lignes de champ électrique, obtenu en soustrayant le nombre de lignes dans le sens de l'extérieur vers l'intérieur du nombre de lignes dans le sens de l'intérieur vers l'extérieur, donne une mesure visuelle du flux électrique à travers les surfaces.

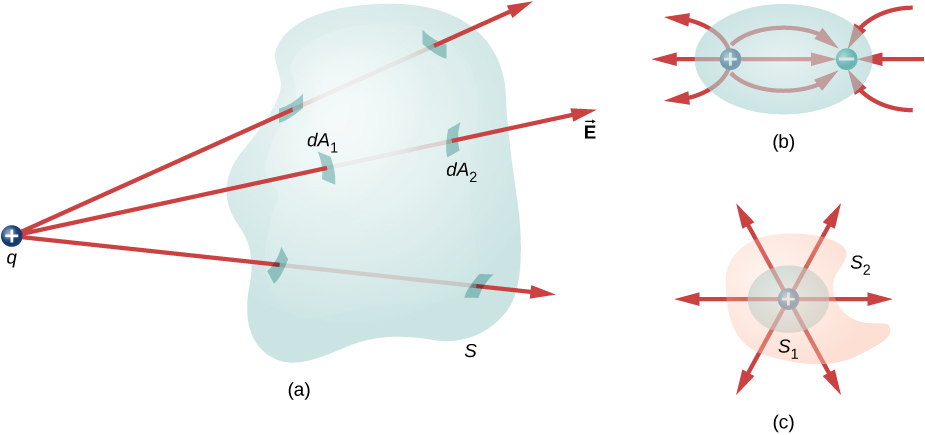
    Vous pouvez voir que si aucune charge n'est incluse dans une surface fermée, le flux électrique qui la traverse doit être nul. Une ligne de champ typique entre à la surface\(dA_1\) et en sort à\(dA_2\). Chaque ligne qui entre dans la surface doit également quitter cette surface. Le « flux » net des lignes de champ entrant ou sortant de la surface est donc nul (Figure\(\PageIndex{3a}\)). La même chose se produit si des charges de signe égal et opposé sont incluses à l'intérieur de la surface fermée, de sorte que la charge totale incluse est nulle (Figure\(\PageIndex{3b}\)). Une surface qui contient la même quantité de charge est traversée par le même nombre de lignes de champ, quelles que soient la forme ou la taille de la surface, tant que la surface contient la même quantité de charge (Figure\(\PageIndex{3c}\)).

    La figure a montre une forme tridimensionnelle irrégulière étiquetée S. Un petit cercle avec un signe plus, nommé q, se trouve à l'extérieur. Trois flèches étiquetées vecteur E partent de q et passent par S. Les zones où les flèches percent la surface de S sont mises en évidence. Le patch où une flèche entre dans la forme est étiqueté dA1 et le patch où la flèche émerge de la forme est étiqueté dA2. La figure b montre un ovale avec deux petits cercles à l'intérieur. Ils sont étiquetés plus et moins. Trois flèches partant de l'extérieur de l'ovale pointent vers le cercle marqué « moins ». Trois flèches pointent du plus vers le moins. Trois flèches pointent du plus vers l'extérieur de l'ovale. La figure c a une forme irrégulière étiquetée S2. À l'intérieur se trouve un cercle nommé S1. Au centre se trouve un petit cercle marqué plus. Six flèches rayonnent vers l'extérieur à partir d'ici dans des directions différentes.
    Figure\(\PageIndex{3}\) : Comprendre le flux en termes de lignes de champ. (a) Le flux électrique à travers une surface fermée dû à une charge à l'extérieur de cette surface est nul. (b) Les charges sont fermées, mais comme la charge nette incluse est nulle, le flux net à travers la surface fermée est également nul. (c) La forme et la taille des surfaces qui entourent une charge n'ont pas d'importance car toutes les surfaces contenant la même charge ont le même flux.

    Déclaration de la loi de Gauss

    La loi de Gauss généralise ce résultat au cas de n'importe quel nombre de charges et de n'importe quel emplacement des charges dans l'espace à l'intérieur de la surface fermée. Selon la loi de Gauss, le flux du champ électrique\(\vec{E}\) à travers toute surface fermée, également appelée surface gaussienne, est égal à la charge nette incluse\((q_{enc})\) divisée par la permittivité de l'espace libre\((\epsilon_0)\) :

    \[\Phi_{Closed \, Surface} = \dfrac{q_{enc}}{\epsilon_0}.\]

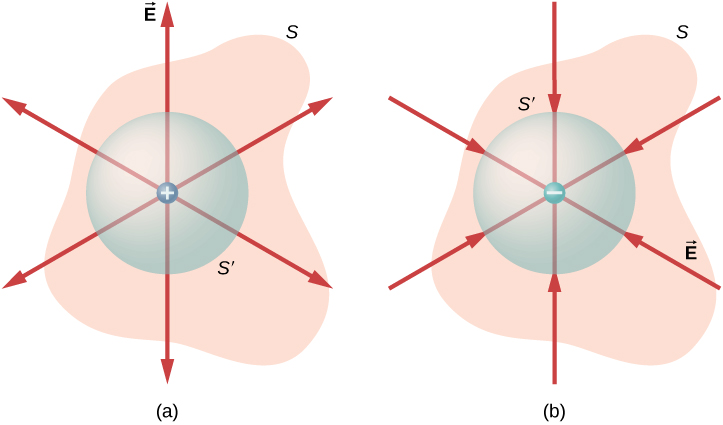
    Cette équation est valable pour les charges de l'un ou l'autre signe, car nous définissons le vecteur de surface d'une surface fermée pour pointer vers l'extérieur. Si la charge incluse est négative (Figure\(\PageIndex{4b}\)), le flux traversant l'une\(S\) ou l'autre\(S'\) est négatif.

    La figure a une forme irrégulière étiquetée S. À l'intérieur de celle-ci se trouve un cercle étiqueté S prime. Au centre se trouve un petit cercle marqué plus. Six flèches rayonnent vers l'extérieur à partir d'ici dans des directions différentes. La figure b a la même forme irrégulière S et le même cercle S prime. Au centre se trouve un petit cercle marqué moins. Six flèches provenant de directions différentes pointent vers l'intérieur vers le signe moins.
    Figure\(\PageIndex{4}\) : Le flux électrique à travers toute surface fermée entourant une charge ponctuelle q est donné par la loi de Gauss. (a) La charge incluse est positive. (b) La charge incluse est négative.

    La surface gaussienne n'a pas besoin de correspondre à un objet physique réel ; en fait, elle le fera rarement. C'est une construction mathématique qui peut avoir n'importe quelle forme, à condition qu'elle soit fermée. Cependant, comme notre objectif est d'intégrer le flux qui le traverse, nous avons tendance à choisir des formes hautement symétriques.

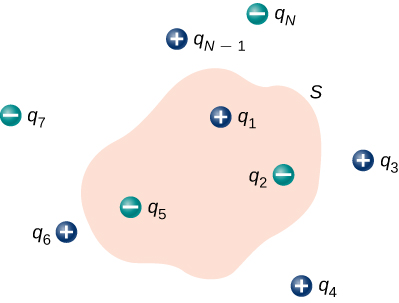
    Si les frais sont des frais ponctuels discrets, il suffit de les ajouter. Si la charge est décrite par une distribution continue, nous devons procéder à une intégration appropriée pour trouver la charge totale qui se trouve à l'intérieur du volume fermé. Par exemple, le flux à travers la surface gaussienne\(S\) de la figure\(\PageIndex{5}\) est

    \[\Phi = (q_1 + q_2 + q_5)/\epsilon_0.\]

    Notez qu'il\(q_{enc}\) s'agit simplement de la somme des points facturés. Si la distribution de charge était continue, nous aurions besoin d'une intégration appropriée pour calculer la charge totale au sein de la surface gaussienne.

    La figure montre une forme irrégulière étiquetée S. À l'intérieur de celle-ci se trouvent des charges étiquetées positives q1 et négatives q2 et q5. À l'extérieur de S se trouvent des charges étiquetées positives q3, q4, q6 et q N moins 1 et négatives q7 et q N.
    Figure\(\PageIndex{5}\) : Le flux à travers la surface gaussienne illustré, en raison de la distribution de charge, est\(\Phi = (q_1 + q_2 + q_5)/\epsilon_0\).

    Rappelons que le principe de superposition vaut pour le champ électrique. Par conséquent, le champ électrique total en tout point, y compris ceux de la surface gaussienne choisie, est la somme de tous les champs électriques présents à ce point. Cela nous permet d'écrire la loi de Gauss en termes de champ électrique total.

    Loi de Gauss

    Le flux\(\Phi\) du champ électrique\(\vec{E}\) à travers toute surface fermée S (surface gaussienne) est égal à la charge nette incluse\((q_{enc})\) divisée par la permittivité de l'espace libre\((\epsilon_0)\) :

    \[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \dfrac{q_{enc}}{\epsilon_0}.\]

    Pour utiliser efficacement la loi de Gauss, vous devez avoir une compréhension claire de ce que représente chaque terme de l'équation. Le champ\(\vec{E}\) est le champ électrique total en tout point de la surface gaussienne. Ce champ total inclut les contributions des charges à la fois à l'intérieur et à l'extérieur de la surface gaussienne. Cependant,\(q_{enc}\) c'est juste la charge à l'intérieur de la surface gaussienne. Enfin, la surface gaussienne est toute surface fermée de l'espace. Cette surface peut coïncider avec la surface réelle d'un conducteur, ou il peut s'agir d'une surface géométrique imaginaire. La seule exigence imposée à une surface gaussienne est qu'elle soit fermée (Figure\(\PageIndex{5}\)).

    La figure montre une bouteille qui ressemble à une fiole renversée dont le col est allongé, plié vers le haut, tordu, introduit à l'intérieur du flacon et joint à sa base, ne présentant ainsi qu'une seule surface.
    Figure\(\PageIndex{6}\) : Une bouteille Klein partiellement remplie d'un liquide. La bouteille Klein pourrait-elle être utilisée comme surface gaussienne ?
    Exemple\(\PageIndex{1}\): Electric Flux through Gaussian Surfaces

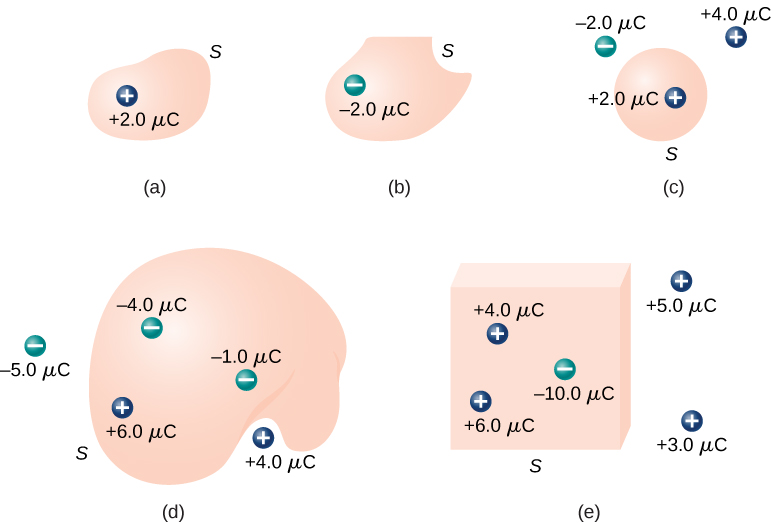
    Calculez le flux électrique à travers chaque surface gaussienne illustrée à la figure\(\PageIndex{7}\).

    Les figures a à d montrent des formes irrégulières et la figure e montre un cube. La figure a une charge à l'intérieur de la forme étiquetée plus 2,0 mu C. La figure b a une charge à l'intérieur de la forme étiquetée moins 2,0 mu C. La figure c a une charge à l'intérieur de la forme étiquetée plus 2,0 mu C et deux charges à l'extérieur étiquetées plus 4 mu C et moins 2,0 mu C. La figure d a trois charges à l'intérieur de la forme étiquetée moins 1,0 mu. C, moins 4,0 mu C et plus 6,0 mu C et deux charges en dehors de la forme étiquetée moins 5,0 mu C et plus 4,0 mu C. La figure e contient trois charges intérieures étiquetées plus 4,0 mu C, plus 6,0 mu C et moins 10,0 mu C et deux charges à l'extérieur du cube étiquetées plus 5,0 mu C et 3,0 mu C.
    Figure\(\PageIndex{7}\) : Différentes surfaces et charges gaussiennes.

    Stratégie

    D'après la loi de Gauss, le flux à travers chaque surface est donné par\(q_{enc}/\epsilon_0\), où\(q_{enc}\) est la charge enfermée par cette surface.

    Solution

    Pour les surfaces et les charges indiquées, on trouve

    une\(\Phi = \frac{2.0 \, \mu C}{\epsilon_0} = 2.3 \times 10^5 N \cdot m^2/C\).

    \(\Phi = \frac{-2.0 \, \mu C}{\epsilon_0} = -2.3 \times 10^5 N \cdot m^2/C\)b.

    \(\Phi = \frac{2.0 \, \mu C}{\epsilon_0} = 2.3 \times 10^5 N \cdot m^2/C\)c.

    \(\frac{-4.0 \, \mu C + 6.0 \, \mu C - 1.0 \, \mu C}{\epsilon_0} = 1.1 \times 10^5 N \cdot m^2/C\)d.

    \(\frac{4.0 \, \mu C + 6.0 \, \mu C - 10.0 \, \mu C}{\epsilon_0} = 0\)e.

    L'importance

    Dans le cas particulier d'une surface fermée, les calculs de flux deviennent une somme de charges. Dans la section suivante, cela nous permettra de travailler avec des systèmes plus complexes.

    Exercice\(\PageIndex{1}\)

    Calculez le flux électrique à travers la surface cubique fermée pour chaque distribution de charge illustrée à la figure\(\PageIndex{8}\).

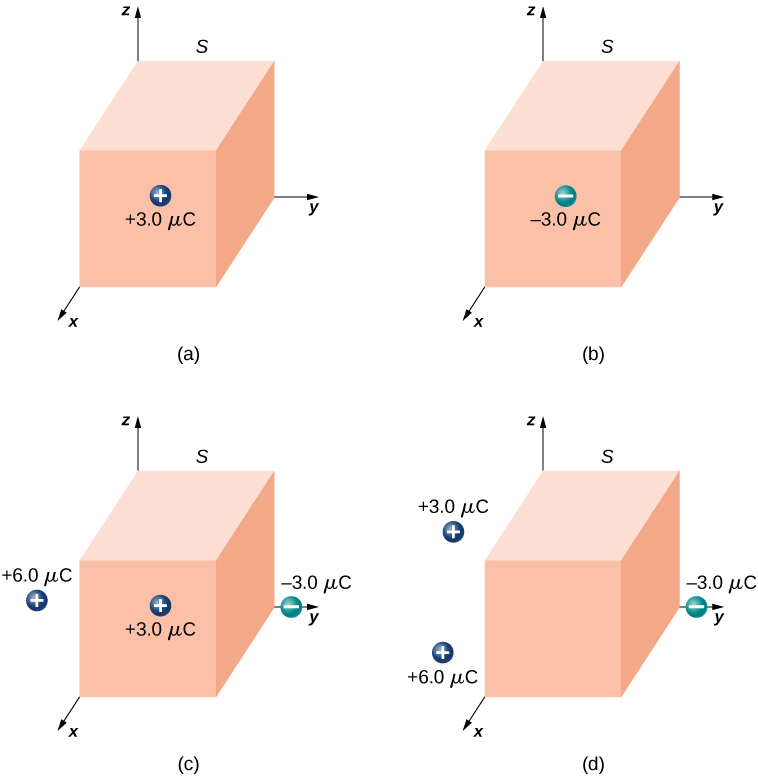
    Les figures a à d montrent un cuboïde avec un coin à l'origine des axes de coordonnées. Sur la figure a, il y a une charge plus 3,0 mu C sur la surface parallèle au plan yz. Sur la figure b, il y a une charge de moins 3,0 mu C sur la surface parallèle au plan yz. Dans la figure c, il y a une charge plus 3,0 mu C sur la surface parallèle au plan yz, une charge moins 3,0 mu C sur l'axe y à l'extérieur de la forme et une charge plus 6,0 mu C à l'extérieur de la forme. Dans la figure d, il y a une charge moins 3,0 mu C sur l'axe y à l'extérieur de la forme et des charges plus 3,0 mu C et plus 6,0 mu C à l'extérieur de la forme.
    Figure\(\PageIndex{8}\) : Une surface gaussienne cubique avec différentes distributions de charges.
    Répondez à une

    \(3.4 \times 10^5 N \cdot m^2/C\)

    Réponse b

    \(-3.4 \times 10^5 N \cdot m^2/C\)

    Réponse c

    \(3.4 \times 10^5 N \cdot m^2/C\)

    Réponse d

    0

    Utilisez cette simulation pour ajuster l'amplitude de la charge et le rayon de la surface gaussienne qui l'entoure. Découvrez comment cela affecte le flux total et l'amplitude du champ électrique à la surface gaussienne.