6.2 : Flux électrique
- Page ID
- 191115
À la fin de cette section, vous serez en mesure de :
- Définir le concept de flux
- Décrire le flux électrique
- Calculer le flux électrique pour une situation donnée
Le concept de flux décrit la quantité de quelque chose qui traverse une zone donnée. Plus formellement, il s'agit du produit scalaire d'un champ vectoriel (dans ce chapitre, le champ électrique) avec une surface. Vous pouvez conceptualiser le flux d'un champ électrique comme une mesure du nombre de lignes de champ électrique traversant une zone (Figure\(\PageIndex{1}\)). Plus la surface est grande, plus les lignes de champ la traversent et, par conséquent, plus le flux est important ; de même, plus le champ électrique est fort (représenté par une plus grande densité de lignes), plus le flux est important. En revanche, si la zone pivote de manière à ce que le plan soit aligné avec les lignes de champ, aucune ne passera et il n'y aura aucun flux.
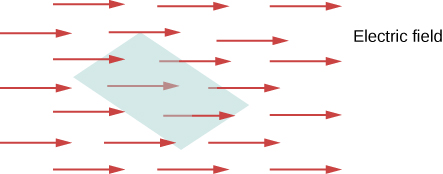
Une analogie macroscopique qui pourrait vous aider à imaginer qu'il s'agit de placer un hula hoop dans une rivière qui coule. Lorsque vous modifiez l'angle du cercle par rapport à la direction du courant, une plus ou moins grande partie du flux traverse le cercle. De même, le débit à travers l'arceau dépend de l'intensité du courant et de la taille de l'arceau. Encore une fois, le flux est un concept général ; nous pouvons également l'utiliser pour décrire la quantité de lumière solaire qui frappe un panneau solaire ou la quantité d'énergie qu'un télescope reçoit d'une étoile lointaine, par exemple.
Pour quantifier cette idée, la figure\(\PageIndex{1a}\) montre\(S_1\) une surface\(A_1\) plane perpendiculaire au champ électrique uniforme\(\vec{E} = E\hat{y}\). Si N lignes de champ traversent\(S_1\), alors nous savons, grâce à la définition des lignes de champ électrique (charges et champs électriques)\(N/A \propto E\), que, ou\(N \propto EA_1\).
La quantité\(EA_1\) est le flux électrique traversant\(S_1\). Nous représentons le flux électrique à travers une surface ouverte, comme\(S_1\) par le symbole\(\Phi\). Le flux électrique est une quantité scalaire et possède une unité SI de newtons-mètres carrés par coulomb (\(N \cdot m^2/C\)). Remarquez que l'on\(N \propto EA_1\) peut également écrire comme\(N \propto \Phi\), démontrant que le flux électrique est une mesure du nombre de lignes de champ traversant une surface.
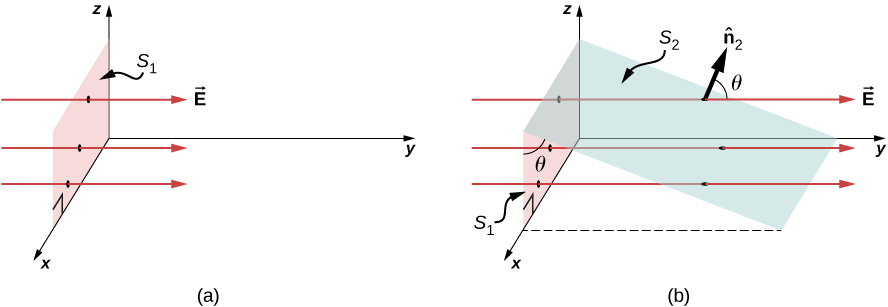
Considérons maintenant une surface plane qui n'est pas perpendiculaire au champ. Comment représenterait-on le flux électrique ? La figure\(\PageIndex{2b}\) montre une surface\(S_2\) d'une zone inclinée\(A_2\) selon un angle\(\theta\) par rapport au plan xz et dont la projection dans ce plan est\(S_1\) (zone\(A_1\)). Les zones sont liées par\(A_2 \, cos \, \theta = A_1\). Comme le même nombre de lignes de champ traverse les deux surfaces\(S_1\) et\(S_2\), les flux à travers les deux surfaces doivent être identiques. Le flux traversant\(S_2\) est donc\(\Phi = EA_1 = EA_2 \, cos \, \theta\). \(\hat{n}_2\)En désignant comme un vecteur unitaire normal à\(S_2\) (voir Figure\(\PageIndex{2b}\)), nous obtenons
\[\Phi = \vec{E} \cdot \hat{n}_2 A_2.\]
Regardez cette vidéo pour observer ce qu'il advient du flux lorsque la surface change de taille et d'angle, ou lorsque l'intensité du champ électrique change.
Vecteur de zone
Pour discuter du flux d'un champ vectoriel, il est utile d'introduire un vecteur de surface\(\vec{A}\). Cela nous permet d'écrire la dernière équation sous une forme plus compacte. Quelle doit être la magnitude du vecteur de surface ? Quelle doit être la direction du vecteur de surface ? Quelles sont les implications de la façon dont vous répondez à la question précédente ?
Le vecteur de surface d'une surface plane de la zone A a la magnitude et la direction suivantes :
- La magnitude est égale à l'aire (A)
- La direction est le long de la normale à la surface\((\hat{n})\), c'est-à-dire perpendiculaire à la surface.
Comme la normale d'une surface plane peut pointer dans les deux sens à partir de la surface, la direction du vecteur de surface d'une surface ouverte doit être choisie, comme indiqué sur la figure\(\PageIndex{3}\).
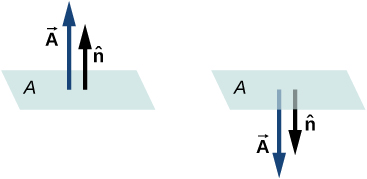
Comme il\(\hat{n}\) s'agit d'une unité normale à une surface, elle possède deux directions possibles en tout point de cette surface (Figure\(\PageIndex{1a}\)). Pour une surface ouverte, nous pouvons utiliser l'une ou l'autre direction, à condition d'être constants sur toute la surface. \(\PageIndex{1c}\)de la figure montre plusieurs cas.
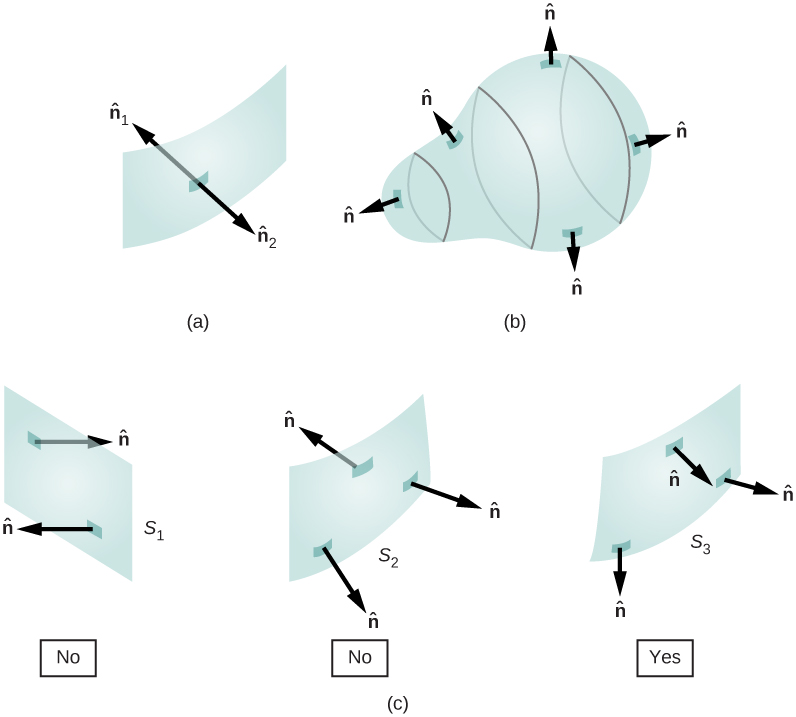
Toutefois, si une surface est fermée, elle entoure un volume. Dans ce cas, la direction du vecteur normal en tout point de la surface pointe de l'intérieur vers l'extérieur. Sur une surface fermée, telle que celle de la figure\(\PageIndex{1b}\),\(\hat{n}\) est choisie comme étant la normale extérieure en tout point, conformément à la convention des signes pour la charge électrique.
Flux électrique
Maintenant que nous avons défini le vecteur de surface d'une surface, nous pouvons définir le flux électrique d'un champ électrique uniforme à travers une zone plane comme le produit scalaire du champ électrique et du vecteur de surface :
\[\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \hat{E}, \, flat \, surface).\]
La figure\(\PageIndex{5}\) montre le champ électrique d'un système à plaques parallèles chargé de manière opposée et d'une boîte imaginaire entre les plaques. Le champ électrique entre les plaques est uniforme et pointe de la plaque positive vers la plaque négative. Un calcul du flux de ce champ à travers les différentes faces de la boîte montre que le flux net à travers la boîte est nul. Pourquoi le flux s'annule-t-il ici ?
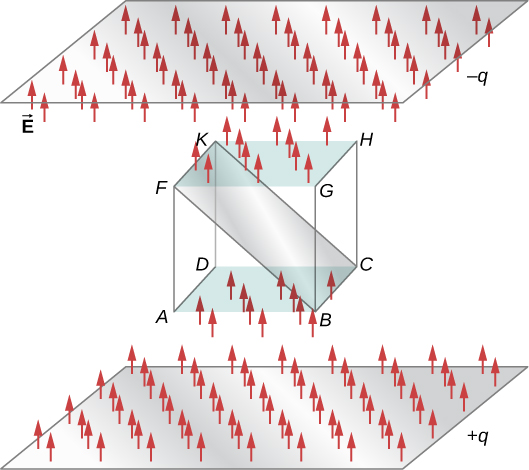
La raison en est que les sources du champ électrique se trouvent à l'extérieur du boîtier. Par conséquent, si une ligne de champ électrique entre dans le volume du boîtier, elle doit également sortir quelque part à la surface, car il n'y a aucune charge à l'intérieur pour que les lignes puissent atterrir. Ainsi, de manière générale, le flux électrique à travers une surface fermée est nul s'il n'y a aucune source de champ électrique, qu'il s'agisse de charges positives ou négatives, à l'intérieur du volume clos. En général, lorsque les lignes de champ quittent (ou « sortent ») d'une surface fermée,\(\Phi\) c'est positif ; lorsqu'elles entrent (ou « entrent ») dans la surface,\(\Phi\) c'est négatif.
Toute surface lisse et non plane peut être remplacée par un ensemble de petites surfaces à peu près plates, comme le montre la figure\(\PageIndex{6}\). Si nous divisons une surface S en petites zones, nous remarquons que, à mesure que les plaques deviennent plus petites, elles peuvent être approximées par des surfaces planes. Cela est similaire à la façon dont nous traitons la surface de la Terre comme étant localement plate, même si nous savons que, globalement, elle est approximativement sphérique.
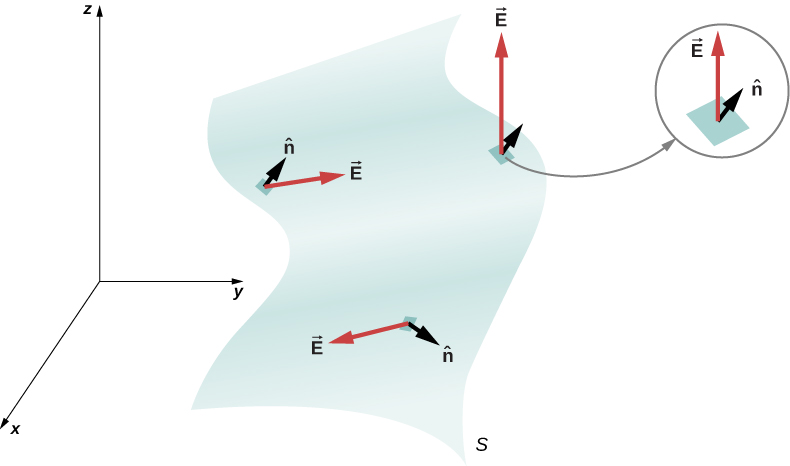
Pour suivre les patchs, nous pouvons les numéroter de 1 à N. Maintenant, nous définissons le vecteur de surface pour chaque patch comme la zone du patch pointée dans la direction de la normale. Dénotons le vecteur de surface pour le dans le patch par\(\delta \vec{A}_i\). (Nous avons utilisé le symbole\(\delta\) pour nous rappeler que la zone correspond à une parcelle arbitrairement petite.) Avec des plaques suffisamment petites, nous pouvons estimer que le champ électrique sur une plaque donnée est uniforme. Dénotons le champ électrique moyen à l'emplacement du dans le patch par\(\vec{E}_i\).
\[\vec{E}_i = \mathrm{average \, electric \, field \, over \, the \,} i \mathrm{th \, patch}.\]
Par conséquent, nous pouvons écrire le flux électrique\(\Phi\) à travers la zone du i ième patch comme
\[\Phi_i = \vec{E}_i \cdot \delta \vec{A}_i \, (i \mathrm{th \, patch}).\]
Le flux à travers chacune des zones individuelles peut être construit de cette manière, puis ajouté pour nous donner une estimation du flux net à travers toute la surface S, que nous désignons simplement par\(\Phi\).
\[\Phi = \sum_{i=1}^N \Phi_i = \sum_{i=1}^N \vec{E}_i \cdot \delta \vec{A}_i \, (N \, patch \, estimate).\]
Cette estimation du flux s'améliore à mesure que nous diminuons la taille des plaques. Toutefois, lorsque vous utilisez des plaques plus petites, vous en avez besoin d'un plus grand nombre pour couvrir la même surface. Dans la limite des zones infinitésimales, elles peuvent être considérées comme ayant une surface dA et une unité normales\(\hat{n}\). Comme les éléments sont infinitésimaux, ils peuvent être supposés planaires et\(\vec{E}_i\) peuvent être considérés comme constants sur n'importe quel élément. Ensuite, le flux\(d\Phi\) à travers une zone dA est donné par\(d\Phi = \vec{E} \cdot \hat{n} dA\). Il est positif lorsque l'angle entre\(\vec{E}_i\) et\(\hat{n}\) est inférieur à\(90^o\) et négatif lorsque l'angle est supérieur à\(90^o\). Le flux net est la somme des éléments de flux infinitésimaux sur toute la surface. Avec des zones infinitésimales, vous avez besoin d'un nombre infini de patchs, et la limite de la somme devient une intégrale de surface. En\(\int_S\) représentant l'intégrale sur S,
\[\Phi = \int_S \vec{E} \cdot \hat{n}dA = \int_S \vec{E} \cdot d\vec{A} \, (open \, surface).\]
Concrètement, les intégrales de surface sont calculées en prenant les antidérivées des deux dimensions définissant la surface, les bords de la surface en question étant les limites de l'intégrale.
Pour faire la distinction entre le flux à travers une surface ouverte comme celle de la Figure\(\PageIndex{2}\) et le flux à travers une surface fermée (une surface qui délimite complètement un certain volume), nous représentons le flux à travers une surface fermée par
\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = \oint_S \vec{E} \cdot d\vec{A} \, (closed \, surface)\]
où le cercle passant par le symbole intégral signifie simplement que la surface est fermée et que nous nous intégrons sur l'ensemble. Si vous n'intégrez que sur une partie d'une surface fermée, cela signifie que vous traitez un sous-ensemble de celle-ci comme une surface ouverte.
Un champ électrique constant de magnitude\(E_0\) pointe dans la direction de l'axe z positif (Figure\(\PageIndex{7}\)). Quel est le flux électrique à travers un rectangle de côtés a et b dans le plan (a) xy et dans le plan (b) xz ?
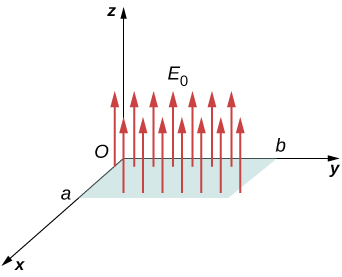
Stratégie
Appliquez la définition du flux :\(\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \vec{E})\), où la définition du produit scalaire est cruciale.
Solution
- Dans ce cas,\(\Phi = \vec{E}_0 \cdot \vec{A} = E_0 A = E_0 ab\).
- Ici, la direction du vecteur de surface est soit le long de l'axe y positif, soit vers l'axe y négatif. Par conséquent, le produit scalaire du champ électrique avec le vecteur de surface est nul, ce qui donne un flux nul.
L'importance
Les directions relatives du champ électrique et de la surface peuvent faire en sorte que le flux à travers la zone soit nul.
Un champ électrique constant de magnitude\(E_0\) pointe dans la direction de l'axe z positif (Figure\(\PageIndex{8}\)). Quel est le flux électrique net à travers un cube ?

Stratégie
Appliquez la définition du flux :\(\Phi = \vec{E} \cdot \vec{A} \, (uniform \, \vec{E})\) en notant qu'une surface fermée élimine l'ambiguïté dans la direction du vecteur de surface.
Solution
À travers la face supérieure du cube\(\Phi = \vec{E}_0 \cdot \vec{A} = E_0 A\).
Par la face inférieure du cube\(\Phi = \vec{E}_0 \cdot \vec{A} = - E_0 A\), car le vecteur de surface pointe ici vers le bas.
Le long des quatre autres côtés, la direction du vecteur de surface est perpendiculaire à la direction du champ électrique. Par conséquent, le produit scalaire du champ électrique avec le vecteur de surface est nul, ce qui donne un flux nul.
Le flux net est de\(\Phi_{net} = E_0A - E_0 A + 0 + 0 + 0 + 0 = 0\).
L'importance
Le flux net d'un champ électrique uniforme à travers une surface fermée est nul.
Un champ électrique uniforme\(\vec{E}\) de magnitude 10 N/C est dirigé parallèlement au plan yz\(30^o\) au-dessus du plan xy, comme le montre la figure\(\PageIndex{9}\). Quel est le flux électrique à travers la surface plane de la zone\(6.0 \, m^2\) située dans le plan xz ? Supposons que cela\(\hat{n}\) pointe dans la direction y positive.
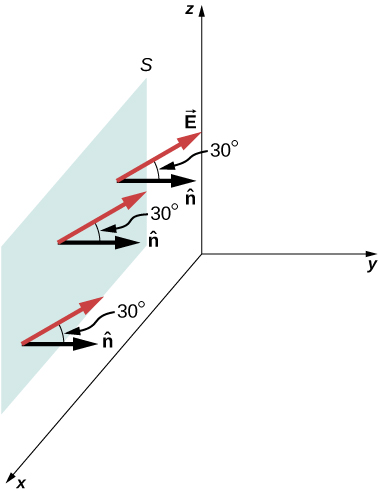
Stratégie
Appliquer\(\Phi = \int_S \vec{E} \cdot \hat{n} dA\), là où la direction et l'amplitude du champ électrique sont constantes.
Solution
L'angle entre le champ électrique uniforme\(\vec{E}\) et l'unité perpendiculaire\(\hat{n}\) à la surface plane est de\(30^o\). Comme la direction et l'amplitude sont constantes, E sort de l'intégrale. Il ne reste plus qu'une surface intégrale sur dA, qui est A. Par conséquent, en utilisant l'équation de surface ouverte, nous trouvons que le flux électrique à travers la surface est
\[\Phi = \int_S \vec{E} \cdot \hat{n} dA = EA \, cos \, \theta\]
\[= (10 \, N/C)(6.0 \, m^2)(cos \, 30^o) = 52 \, N \cdot m^2/C.\]
L'importance
Encore une fois, les directions relatives du champ et de la surface sont importantes, et l'équation générale avec l'intégrale se simplifiera pour obtenir le simple produit scalaire de la surface et du champ électrique.
Quel angle doit-il y avoir entre le champ électrique et la surface illustrée à la figure\(\PageIndex{9}\) dans l'exemple précédent afin qu'aucun flux électrique ne traverse la surface ?
Solution
Placez-le de manière à ce que son unité normale soit perpendiculaire à\(\vec{E}\).
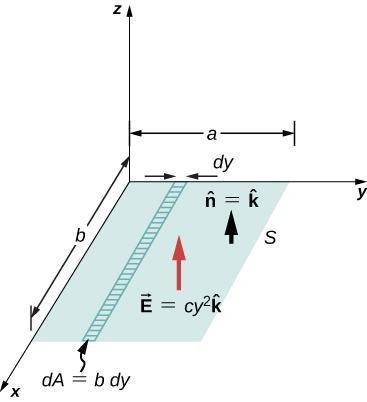
Quel est le flux total du champ électrique\(\vec{E} = cy^2\hat{k}\) à travers la surface rectangulaire illustrée à la figure\(\PageIndex{10}\) ?
Stratégie
Appliquer\(\Phi = \int_S \vec{E} \cdot \hat{n}dA\). Nous supposons que l'unité normale\(\hat{n}\) à la surface donnée pointe dans la direction z positive, donc\(\hat{n} = \hat{k}\). Le champ électrique n'étant pas uniforme sur la surface, il est nécessaire de diviser la surface en bandes infinitésimales le long desquelles\(\vec{E}\) il est essentiellement constant. Comme le montre la figure\(\PageIndex{10}\), ces bandes sont parallèles à l'axe x et chaque bande possède une surface\(dA = b \, dy\).
Solution
À partir de l'intégrale de la surface ouverte, nous trouvons que le flux net à travers la surface rectangulaire est
\[\begin{align*} \Phi &= \int_S \vec{E} \cdot \hat{n} dA = \int_0^a (cy^2 \hat{k}) \cdot \hat{k}(b \, dy) \\[4pt] &= cb \int_0^a y^2 dy = \frac{1}{3} a^3 bc. \end{align*}\]
L'importance
Pour un champ électrique non constant, la méthode intégrale est requise.
Si le champ électrique dans l'exemple\(\PageIndex{4}\) est\(\vec{E} = mx\hat{k}\)... quel est le flux à travers la zone rectangulaire ?
Solution
\(mab^2/2\)


