6.4 : Appliquer la loi de Gauss

Last updated
Save as PDF

Page ID: 191111

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Expliquer ce que sont les symétries sphérique, cylindrique et plane
Reconnaître si un système donné possède ou non l'une de ces symétries
Appliquez la loi de Gauss pour déterminer le champ électrique d'un système présentant l'une de ces symétries

La loi de Gauss est très utile pour déterminer les expressions du champ électrique, même si elle ne concerne pas directement le champ électrique ; elle concerne le flux électrique. Il s'avère que dans des situations présentant certaines symétries (sphériques, cylindriques ou planes) dans la distribution de la charge, nous pouvons déduire le champ électrique en fonction de la connaissance du flux électrique. Dans ces systèmes, on peut trouver une surface gaussienne S sur laquelle le champ électrique a une amplitude constante. De plus, il\(\vec{E}\) est parallèle à n'\(\hat{n}\)importe quel endroit de la surface, alors\(\vec{E} \cdot \hat{n} = E\). (Si\(\vec{E}\) et\(\hat{n}\) sont antiparallèles partout sur la surface,\(\vec{E} \cdot \hat{n} = - E\).) La loi de Gauss simplifie alors

\[\Phi = \oint_S \vec{E} \cdot \hat{n} dA = E \oint_S dA = EA = \dfrac{q_{enc}}{\epsilon_0},\]

où A est l'aire de la surface. Notez que ces symétries conduisent à la transformation de l'intégrale du flux en un produit de l'amplitude du champ électrique et d'une surface appropriée. Lorsque vous utilisez ce flux dans l'expression de la loi de Gauss, vous obtenez une équation algébrique que vous pouvez résoudre pour l'amplitude du champ électrique, qui ressemble à

\[E \approx \dfrac{q_{enc}}{\epsilon_0 \, area}.\]

La direction du champ électrique au point P est obtenue à partir de la symétrie de la distribution de charge et du type de charge dans la distribution. Par conséquent, la loi de Gauss peut être utilisée pour déterminer\(\vec{E}\). Voici un résumé des étapes que nous allons suivre :

Stratégie de résolution de problèmes : la loi de Gauss

Identifiez la symétrie spatiale de la distribution de charge. Il s'agit d'une première étape importante qui nous permet de choisir la surface gaussienne appropriée. Par exemple, une charge ponctuelle isolée possède une symétrie sphérique et une ligne de charge infinie possède une symétrie cylindrique.
Choisissez une surface gaussienne présentant la même symétrie que la distribution de charge et identifiez ses conséquences. Avec ce choix,\(\vec{E} \cdot \hat{n}\) il est facile de le déterminer sur la surface gaussienne.
Évaluez l'intégrale\(\oint_S \vec{E} \cdot \hat{n} dA\) sur la surface gaussienne, c'est-à-dire calculez le flux à travers la surface. La symétrie de la surface gaussienne nous permet de prendre\(\vec{E} \cdot \hat{n}\) en compte des facteurs extérieurs à l'intégrale.
Déterminez la quantité de charge entourée par la surface gaussienne. Il s'agit d'une évaluation du côté droit de l'équation représentant la loi de Gauss. Il est souvent nécessaire de réaliser une intégration pour obtenir la charge nette incluse.
Évaluez le champ électrique de la distribution de charge. Le champ peut maintenant être trouvé à l'aide des résultats des étapes 3 et 4.

Fondamentalement, seuls trois types de symétrie permettent d'utiliser la loi de Gauss pour déduire le champ électrique. Ils sont

Une distribution de charge à symétrie sphérique
Une distribution de charge à symétrie cylindrique
Une distribution de charge à symétrie planaire

Pour exploiter la symétrie, nous effectuons les calculs dans les systèmes de coordonnées appropriés et utilisons le type de surface gaussienne approprié pour cette symétrie, en appliquant les quatre étapes restantes.

Distribution de charge avec symétrie sphérique

Une distribution de charge présente une symétrie sphérique si la densité de charge dépend uniquement de la distance par rapport à un point de l'espace et non de la direction. En d'autres termes, si vous faites pivoter le système, il n'aura pas d'apparence différente. Par exemple, si une sphère de rayon R est uniformément chargée en densité de charge\(\rho_0\), la distribution présente une symétrie sphérique (Figure\(\PageIndex{1a}\)). En revanche, si une sphère de rayon R est chargée de telle sorte que la moitié supérieure de la sphère ait une densité de charge uniforme\(\rho_1\) et que la moitié inférieure ait une densité de charge uniforme\(\rho_2 \neq \rho_1\), alors la sphère n'a pas de symétrie sphérique car la densité de charge dépend de la direction (Figure \(\PageIndex{1b}\)). Ainsi, ce n'est pas la forme de l'objet mais la forme de la distribution des charges qui détermine si un système possède ou non une symétrie sphérique.

La figure\(\PageIndex{1c}\) montre une sphère avec quatre coques différentes, chacune ayant sa propre densité de charge uniforme. Bien qu'il s'agisse d'une situation où la densité de charge dans la sphère complète n'est pas uniforme, la fonction de densité de charge dépend uniquement de la distance par rapport au centre et non de la direction. Cette distribution de charge présente donc une symétrie sphérique.

La figure a montre une sphère de couleur uniforme étiquetée rho 0. La figure est étiquetée sphériquement symétrique. La figure b montre une sphère dont les moitiés supérieure et inférieure sont de couleurs différentes. L'hémisphère supérieur est étiqueté rho 1 et l'hémisphère inférieur est étiqueté rho 2. La figure est étiquetée comme ne présentant pas de symétrie sphérique. La figure c montre une sphère, sectionnée pour montrer de nombreuses sphères concentriques de différentes couleurs à l'intérieur de celle-ci. La figure est étiquetée sphériquement symétrique. — Figure\(\PageIndex{1}\) : Illustrations de systèmes sphériquement symétriques et non symétriques. Les différentes nuances indiquent des densités de charge différentes. Les charges sur des objets de forme sphérique ne signifient pas nécessairement que les charges sont distribuées selon une symétrie sphérique. La symétrie sphérique se produit uniquement lorsque la densité de charge ne dépend pas de la direction. Dans (a), les charges sont réparties uniformément dans une sphère. Dans (b), la moitié supérieure de la sphère a une densité de charge différente de celle de la moitié inférieure ; par conséquent, (b) n'a pas de symétrie sphérique. Dans (c), les charges se trouvent dans des couches sphériques de différentes densités de charge, ce qui signifie que la densité de charge est uniquement fonction de la distance radiale par rapport au centre ; par conséquent, le système présente une symétrie sphérique.

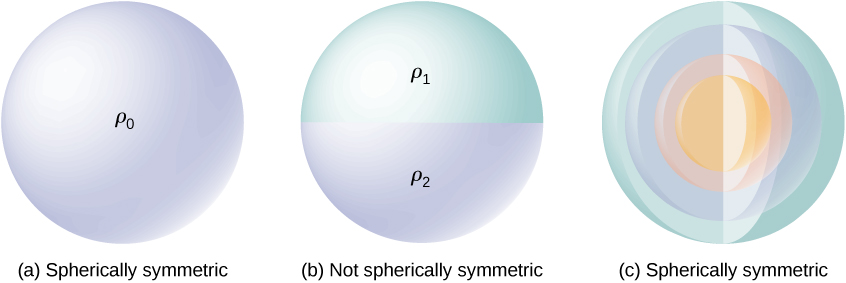
Un bon moyen de déterminer si votre problème est lié à une symétrie sphérique est d'examiner la fonction de densité de charge en coordonnées sphériques\(\rho(r, \theta, \phi)\). Si la densité de charge est uniquement fonction de r\(\rho = \rho(r)\), c'est-à-dire que vous avez une symétrie sphérique. Si la densité dépend de\(\theta\) ou\(\phi\), vous pouvez la modifier par rotation ; vous n'aurez donc pas de symétrie sphérique.

Effets de la symétrie

Dans tous les cas de symétrie sphérique, le champ électrique en tout point doit être dirigé radialement, car la charge et, par conséquent, le champ doivent être invariants lors de la rotation. Par conséquent, en utilisant des coordonnées sphériques dont l'origine se trouve au centre de la distribution de charge sphérique, nous pouvons écrire la forme attendue du champ électrique en un point P situé à une distance r du centre :

\[Spherical \, symmetry: \, \vec{E}_p = E_p(r)\hat{r},\]

où\(\hat{r}\) est le vecteur unitaire pointé dans la direction allant de l'origine au point de champ P. La composante radiale\(E_p\) du champ électrique peut être positive ou négative. Quand\(E_p > 0\), le champ électrique à P pointe loin de l'origine, et quand\(E_p < 0\), le champ électrique à P pointe vers l'origine.

Calculs de surface et de flux gaussiens

Nous pouvons maintenant utiliser cette forme de champ électrique pour obtenir le flux du champ électrique à travers la surface gaussienne. Pour la symétrie sphérique, la surface gaussienne est une surface sphérique fermée qui a le même centre que le centre de la distribution de charge. Ainsi, la direction du vecteur de surface d'un élément de surface sur la surface gaussienne en tout point est parallèle à la direction du champ électrique à ce point, puisqu'ils sont tous deux dirigés radialement vers l'extérieur (Figure\(\PageIndex{2}\)).

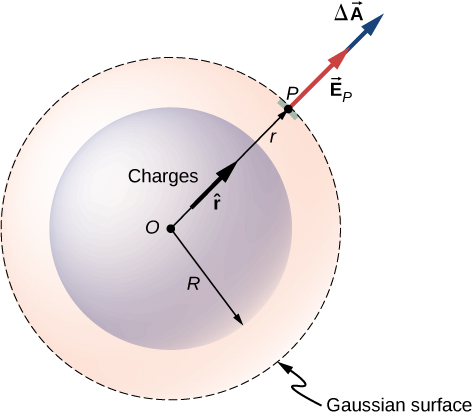
La figure montre un cercle étiqueté charges avec un centre O et un rayon R. Un cercle concentrique plus grand représenté par une ligne pointillée est étiqueté surface gaussienne. Une flèche nommée r indique le rayon du cercle extérieur. Une flèche nommée r qui est représentée le long de r. Une petite zone où r touche la surface gaussienne est mise en évidence et étiquetée P. À partir de là, une autre flèche pointe vers l'extérieur dans la même direction que r. Elle est étiquetée vecteur E indice P. Une autre flèche part de la pointe du vecteur E indice P et pointe vers l'extérieur dans dans la même direction. Il est étiqueté vecteur delta A. — Figure\(\PageIndex{2}\) : Le champ électrique en tout point de la surface sphérique gaussienne pour une distribution de charge sphérique symétrique est parallèle au vecteur de l'élément de surface à ce point, donnant le flux comme le produit de l'amplitude du champ électrique et de la valeur de la surface. Notez que le rayon R de la distribution de charge et le rayon r de la surface gaussienne sont des quantités différentes.

L'amplitude du champ électrique\(\vec{E}\) doit être la même partout sur une surface gaussienne sphérique concentrique à la distribution. Pour une surface sphérique de rayon r :

\[\Phi = \oint_S \vec{E}_p \cdot \hat{n} dA = E_p \oint_S dA = E_p \, 4\pi r^2.\]

Utiliser la loi de Gauss

Selon la loi de Gauss, le flux à travers une surface fermée est égal à la charge totale contenue dans la surface fermée divisée par la permittivité du vide\(\epsilon_0\). \(q_{enc}\)Soit la charge totale comprise entre la distance r et l'origine, qui est l'espace à l'intérieur de la surface sphérique gaussienne de rayon r. Cela donne la relation suivante pour la loi de Gauss :

\[4\pi r^2 E = \dfrac{q_{enc}}{\epsilon_0}.\]

Ainsi, le champ électrique au point P situé à une distance r du centre d'une distribution de charge sphérique symétrique a l'amplitude et la direction suivantes :

\[Magnitude: \, E(r) = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{enc}}{r^2}\]

Direction : radiale de O vers P ou de P vers O.

La direction du champ au point P dépend du fait que la charge dans la sphère est positive ou négative. Pour une charge positive nette enfermée dans la surface gaussienne, la direction est de O vers P, et pour une charge négative nette, la direction est de P vers O. C'est tout ce dont nous avons besoin pour une recharge de points, et vous remarquerez que le résultat ci-dessus est identique à celui d'une recharge de points. Cependant, la loi de Gauss devient vraiment utile dans les cas où la charge occupe un volume fini.

Charge informatique fermée

Le cas le plus intéressant est celui où une distribution de charge sphérique occupe un volume et qu'il devient donc pertinent de se demander quel est le champ électrique à l'intérieur de la distribution de charge. Dans ce cas, la charge incluse dépend de la distance r du point de champ par rapport au rayon de la distribution de charge R, comme indiqué sur la figure\(\PageIndex{3}\).

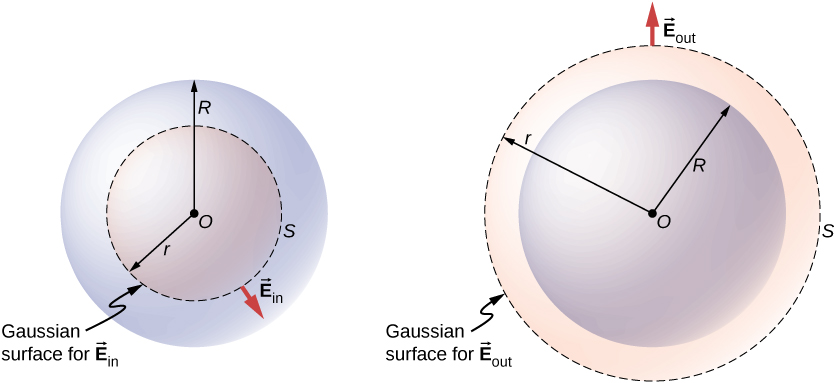
La figure a montre un cercle en pointillés S avec le centre O et le rayon r, et un cercle concentrique plus grand avec le rayon R. Une petite flèche pointe vers l'extérieur à partir de S. Il est étiqueté vecteur E indice in. S est étiqueté surface gaussienne pour l'indice du vecteur E in. La figure b montre un cercle en pointillés S avec un centre O et un rayon r, et un cercle concentrique plus petit avec un rayon R. Une petite flèche pointe vers l'extérieur à partir de S. Il s'agit du vecteur E en indice sortant. S est étiqueté surface gaussienne pour la sortie en indice du vecteur E. — Figure\(\PageIndex{3}\) : Distribution de charge sphérique symétrique et surface gaussienne utilisée pour trouver le champ (a) à l'intérieur et (b) à l'extérieur de la distribution.

Si le point P est situé en dehors de la distribution des charges, c'\(r \geq R\)est-à-dire si, alors la surface gaussienne contenant P entoure toutes les charges de la sphère. Dans ce cas,\(q_{enc}\) est égal à la charge totale dans la sphère. En revanche, si le point P se trouve dans la distribution de charge sphérique, c'est-à-dire si\(r < R\), alors la surface gaussienne entoure une sphère plus petite que la sphère de distribution des charges. Dans ce cas,\(q_{enc}\) est inférieur à la charge totale présente dans la sphère. En se référant à\(\PageIndex{3}\) la figure, nous pouvons écrire\(q_{enc}\) comme

\[q_{enc} = q_{tot} (total \, charge) \, if \, r \geq R\]

\[q_{enc} = q_{within \, r < R} (only \, charge \, within \, r < R) \, if \, r < R\]

Le champ situé à un point situé en dehors de la distribution de charge est également appelé\(\vec{E}_{out}\), et le champ situé à un point situé à l'intérieur de la distribution de charge est appelé\(\vec{E}_{in}\). En nous concentrant sur les deux types de points de champ, à l'intérieur ou à l'extérieur de la distribution de charge, nous pouvons maintenant écrire l'amplitude du champ électrique comme

\[P \, outside \, sphere \, E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}\]

\[P \, inside \, sphere \, E_{in} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{within \, r < R}}{r^2}.\]

Notez que le champ électrique en dehors d'une distribution de charge sphérique symétrique est identique à celui d'une charge ponctuelle au centre qui a une charge égale à la charge totale de la distribution de charge sphérique. Cela est remarquable puisque les charges ne se situent pas uniquement au centre. Nous élaborons maintenant des exemples spécifiques de distributions de charges sphériques, en commençant par le cas d'une sphère uniformément chargée.

Sphère chargée uniformément

Une sphère de rayon R, telle que celle illustrée sur la figure\(\PageIndex{3}\), possède une densité de charge volumique uniforme\(\rho_0\). Déterminez le champ électrique à un point situé à l'extérieur de la sphère et à un point situé à l'intérieur de la sphère.

Stratégie

Appliquez la stratégie de résolution de problèmes de la loi de Gauss, dans laquelle nous avons déjà élaboré le calcul du flux.

Solution

La charge enfermée par la surface gaussienne est donnée par

\[q_{enc} = \int \rho_0 dV = \int_0^r \rho_0 4\pi r'^2 dr' = \rho \left(\dfrac{4}{3} \pi r^3\right).\]

La réponse à l'amplitude du champ électrique peut alors être écrite immédiatement pour un point situé à l'extérieur de la sphère, étiqueté,\(E_{out}\) et un point à l'intérieur de la sphère, étiqueté\(E_{in}\).

\[E_{out} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}}{r^2}, \, q_{tot} = \dfrac{4}{3} \pi R^3 \, \rho_0,\]

\[E_{in} = \dfrac{q_{enc}}{4\pi \epsilon_0 r^2} = \dfrac{\rho_0r}{3 \epsilon_0}, \, since \, q_{enc} = \dfrac{4}{3} \pi r^3 \rho_0.\]

Il est intéressant de noter que l'amplitude du champ électrique augmente à l'intérieur du matériau lorsque vous sortez, car la quantité de charge enfermée par la surface gaussienne augmente avec le volume. Plus précisément, la charge incluse augmente\(\propto r^3\), tandis que le champ de chaque élément de charge infinitésimal diminue,\(\propto 1/r^2\) avec pour résultat net que le champ électrique au sein de la distribution augmente en intensité linéairement avec le rayon. L'amplitude du champ électrique à l'extérieur de la sphère diminue à mesure que vous vous éloignez des charges, car la charge incluse reste la même mais la distance augmente. La figure\(\PageIndex{4}\) montre la variation de l'amplitude du champ électrique en fonction de la distance par rapport au centre d'une sphère uniformément chargée.

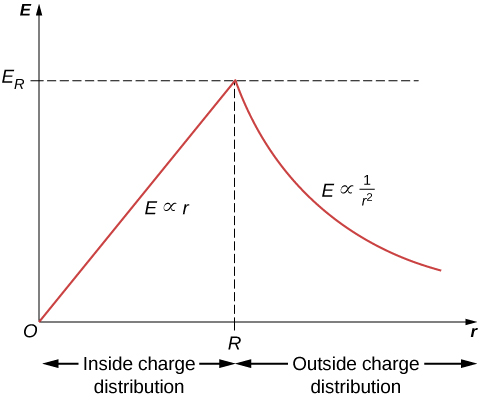
La figure montre un graphique de E par rapport à r. La courbe monte sur une ligne droite nommée E proportionnel à r, culmine et descend sur une ligne courbe marquée E proportionnelle à 1 par r au carré. Le pic a une valeur x de R et une valeur y de l'indice E R. — Figure\(\PageIndex{4}\) : Le champ électrique d'une sphère non conductrice chargée uniformément augmente à l'intérieur de la sphère jusqu'à son maximum à la surface, puis diminue au fur et à mesure que\(1/r^2\). Ici,\(E_R = \frac{\rho_0 R}{3 \epsilon_0}\). Le champ électrique est dû à une distribution de charge sphérique présentant une densité de charge uniforme et une charge totale Q en fonction de la distance par rapport au centre de la distribution.

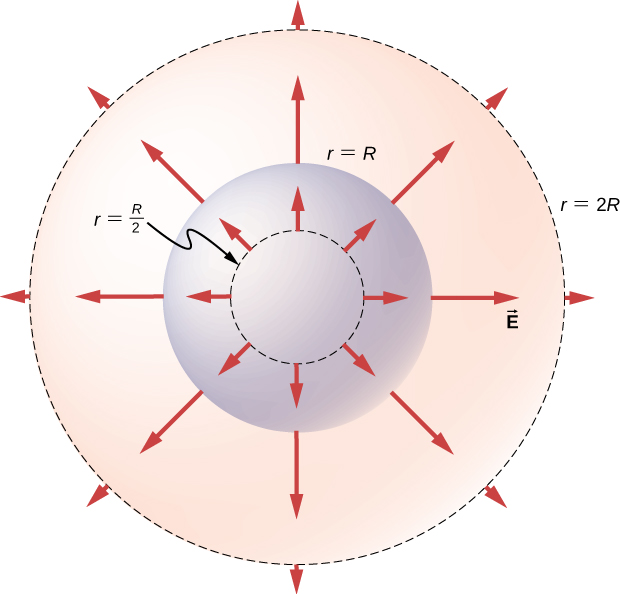
La direction du champ électrique en tout point P est radialement vers l'extérieur depuis l'origine si elle\(\rho_0\) est positive, et vers l'intérieur (c'est-à-dire vers le centre) si elle\(\rho_0\) est négative. Le champ électrique à certains points spatiaux représentatifs est affiché sur la figure\(\PageIndex{5}\) dont les coordonnées radiales r sont\(r = R/2, \, r = R,\) et\(r = 2R\).

La figure montre trois cercles concentriques. Le plus petit est pointillé et marqué r égal à R par 2. Le milieu est marqué r égal à R et le plus grand, également pointillé, est marqué r égal à 2R. Les flèches étiquetées vecteur E partent de chaque cercle et pointent vers l'extérieur, perpendiculairement au cercle. Celles du cercle extérieur sont les plus petites et celles du cercle du milieu sont les plus longues. — Figure\(\PageIndex{5}\) : Vecteurs de champ électrique à l'intérieur et à l'extérieur d'une sphère uniformément chargée.

L'importance

Remarquez que cela\(E_{out}\) a la même forme que l'équation du champ électrique d'une charge ponctuelle isolée. En déterminant le champ électrique d'une distribution de charge sphérique uniforme, nous pouvons donc supposer que toute la charge à l'intérieur de la surface gaussienne sphérique appropriée est située au centre de la distribution.

Sphère chargée de manière non uniforme

Une sphère non conductrice de rayon R possède une densité de charge non uniforme qui varie avec la distance par rapport à son centre, telle que donnée par

\[\rho(r) = ar^n (r \leq R; \, n \geq 0), \nonumber\]

où a est une constante. Nous exigeons\(n \geq 0\) que la densité de charge ne soit pas indéfinie à\(r = 0\). Déterminez le champ électrique à un point situé à l'extérieur de la sphère et à un point situé à l'intérieur de la sphère.

Stratégie

Appliquez la stratégie de la loi de Gauss présentée ci-dessus, dans laquelle nous élaborons les intégrales de charge incluses séparément pour les affaires internes et externes à la sphère.

Solution

Comme la fonction de densité de charge donnée n'a qu'une dépendance radiale et ne dépend pas de la direction, nous avons une situation sphérique symétrique. Par conséquent, l'amplitude du champ électrique en tout point est donnée ci-dessus et la direction est radiale. Nous avons juste besoin de trouver la charge incluse\(q_{enc}\), qui dépend de l'emplacement du point de champ.

Remarque sur les symboles : nous utilisons r\(r'\) pour localiser les charges dans la distribution des charges et r pour localiser le ou les points de champ sur la ou les surfaces gaussiennes. La lettre R est utilisée pour le rayon de la distribution de charge.

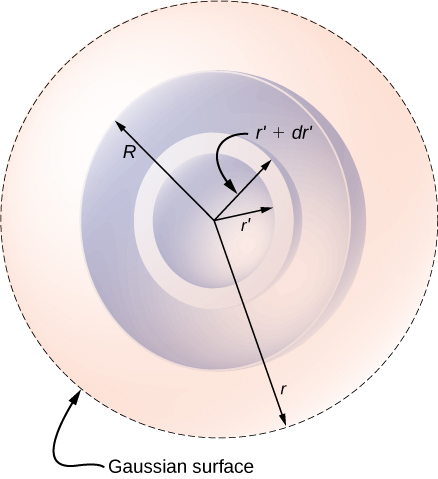
La densité de charge n'étant pas constante ici, nous devons intégrer la fonction de densité de charge sur le volume délimité par la surface gaussienne. Par conséquent, nous avons défini le problème pour les charges dans une coque sphérique, disons entre\(r'\) et\(r' + dr'\) comme indiqué sur la figure\(\PageIndex{6}\). Le volume des charges dans la coque de largeur infinitésimale est égal au produit de la surface\(4\pi r'^2\) et de l'épaisseur\(dr'\). En multipliant le volume par la densité à cet endroit, c'est-à-dire\(ar'^n\), on obtient la charge dans la coque :

\[dq = ar'^n 4\pi r'^2 dr'. \nonumber\]

La figure montre quatre cercles concentriques. En partant du plus petit, leurs rayons sont étiquetés : r prime, r prime plus d r prime, R et r. Le cercle le plus extérieur est pointillé et étiqueté surface gaussienne. — Figure\(\PageIndex{6}\) : Symétrie sphérique avec distribution de charge non uniforme. Dans ce type de problème, nous avons besoin de quatre rayons : R est le rayon de la distribution de charge, r est le rayon de la surface gaussienne,\(r'\) est le rayon intérieur de la coque sphérique et\(r' + dr'\) est le rayon extérieur de la coque sphérique. La coque sphérique est utilisée pour calculer la charge contenue dans la surface gaussienne. La plage pour\(r'\) va de 0 à r pour le champ à un point situé à l'intérieur de la distribution de charge et de 0 à R pour le champ situé en dehors de la distribution de charge. Si\(r > R\), alors la surface gaussienne contient plus de volume que la distribution de charge, mais le volume supplémentaire n'y contribue pas\(q_{enc}\).

(a) Champ situé en dehors de la distribution de charge. Dans ce cas, la surface gaussienne, qui contient le point de champ P, a un rayon r supérieur au rayon R de la distribution des charges,\(r > R\). Par conséquent, toutes les charges de la distribution des charges sont enfermées dans la surface gaussienne. Notez que l'espace entre\(r' = R\) et\(r' = r\) est vide de charges et ne contribue donc pas à l'intégrale sur le volume délimité par la surface gaussienne :

\[q_{enc} = \int dq = \int_0^R ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} R^{n+3}. \nonumber\]

Ceci est utilisé dans le résultat général\(E_{out}\) ci-dessus pour obtenir le champ électrique en un point situé en dehors de la distribution de charge, comme

\[ \vec{E}_{out} = \left[ \dfrac{aR^{n+3}}{\epsilon_0(n + 3)} \right] \dfrac{1}{r^2} \hat{r}, \nonumber\]

où\(\hat{r}\) est un vecteur unitaire dans la direction allant de l'origine au point de champ sur la surface gaussienne.

(b) Champ situé à un point situé à l'intérieur de la distribution de charge. La surface gaussienne est maintenant enterrée dans la distribution de charge, avec\(r < R\). Par conséquent, seules les charges de la distribution qui se trouvent à une distance r du centre de la distribution des charges sphériques sont prises en compte dans\(r_{enc}\) :

\[q_{enc} = \int_0^r ar'^n 4\pi r'^2 dr' = \dfrac{4\pi a}{n + 3} r^{n+3}. \nonumber\]

Maintenant, en utilisant le résultat général ci-dessus pour\(\vec{E}_{in}\), nous trouvons le champ électrique en un point situé à une distance r du centre et situé dans la distribution de charge comme

\[\vec{E}_{in} = \left[ \dfrac{a}{\epsilon_0 ( n + 3)} \right] r^{n+1} \hat{r}, \nonumber\]

où les informations de direction sont incluses en utilisant le vecteur radial unitaire.

Exercice\(\PageIndex{1}\)

Vérifiez que les champs électriques de la sphère sont réduits aux valeurs correctes pour une charge ponctuelle.

Solution

Dans ce cas, il n'y a que\(\vec{E}_{out}\). Donc, oui.

Distribution de charge avec symétrie cylindrique

Une distribution de charge présente une symétrie cylindrique si la densité de charge dépend uniquement de la distance r par rapport à l'axe d'un cylindre et ne doit pas varier le long de l'axe ou selon la direction autour de l'axe. En d'autres termes, si votre système varie si vous le faites pivoter autour de l'axe ou si vous le déplacez le long de l'axe, vous n'avez pas de symétrie cylindrique.

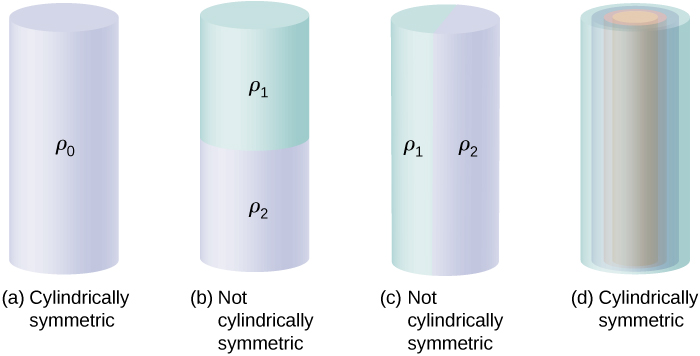
La figure\(\PageIndex{7}\) montre quatre situations dans lesquelles les charges sont réparties dans un cylindre. Une densité de charge uniforme\(\rho_0\) dans un fil droit infini possède une symétrie cylindrique, de même qu'un cylindre infiniment long avec une densité de charge constante\(\rho_0\). Un cylindre infiniment long qui possède différentes densités de charge sur sa longueur, telles qu'une densité de charge\(\rho_1\) pour\(z > 0\) et\(\rho_2 \neq \rho_1\) pour\(z < 0\), ne possède pas de symétrie cylindrique utilisable pour ce parcours. Il en va de même pour un cylindre dans lequel la densité de charge varie avec la direction, comme une densité de charge\(\rho_1\) pour\(0 \leq \theta < \pi\) et\(\rho_2 \neq \rho_1\) pour\(\pi \leq \theta < 2\pi\). Un système avec des coques cylindriques concentriques, chacune ayant des densités de charge uniformes, bien que différentes selon les couches, comme dans FiFigure\(\PageIndex{7d}\), possède une symétrie cylindrique si elles sont infiniment longues. L'exigence de longueur infinie est due à la variation de la densité de charge le long de l'axe d'un cylindre fini. Dans les systèmes réels, nous n'avons pas de cylindres infinis ; cependant, si l'objet cylindrique est considérablement plus long que le rayon de celui-ci qui nous intéresse, alors l'approximation d'un cylindre infini devient utile.

Les figures a à d montrent un cylindre. Sur la figure a, étiquetée cylindriquement symétrique, le cylindre est uniformément coloré et étiqueté rho zéro. Sur la figure b, étiquetée sans symétrie cylindrique, les moitiés supérieure et inférieure du cylindre sont de couleur différente. Le haut est étiqueté rho 1 et le bas est étiqueté rho 2. Sur la figure c, étiquetée sans symétrie cylindrique, les moitiés gauche et droite du cylindre sont de couleur différente. La gauche est étiquetée rho 1 et la droite est étiquetée rho 2. Sur la figure d, de nombreuses sections concentriques sont visibles à l'intérieur du cylindre. La figure est étiquetée de manière cylindrique symétrique. — Figure\(\PageIndex{7}\) : Pour déterminer si une distribution de charge donnée présente une symétrie cylindrique, examinez la section transversale d'un cylindre « infiniment long ». Si la densité de charge ne dépend pas de l'angle polaire de la section transversale ou le long de l'axe, vous avez alors une symétrie cylindrique. (a) La densité de charge est constante dans le cylindre ; (b) la moitié supérieure du cylindre a une densité de charge différente de celle de la moitié inférieure ; (c) la moitié gauche du cylindre a une densité de charge différente de celle de la moitié droite ; (d) les charges sont constantes dans différents anneaux cylindriques, mais la densité ne dépend pas de la angle. Les cas (a) et (d) ont une symétrie cylindrique, alors que (b) et (c) n'en ont pas.

Conséquences de SayMetry

Dans tous les cas de symétrie cylindrique, le champ électrique\(E_p\) en tout point\(P\) doit également présenter une symétrie cylindrique.

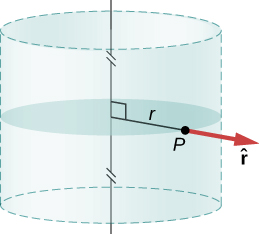
Symétrie cylindrique :\(\vec{E}_p = E_p(r)\hat{r}\), où\(r\) est la distance par rapport à l'axe et\(\hat{r}\) est un vecteur unitaire dirigé perpendiculairement à l'axe (Figure\(\PageIndex{8}\)).

Un cylindre est représenté par une ligne pointillée. Une partie circulaire à l'intérieur du cylindre, en son centre, est mise en évidence. Le rayon du cercle et celui du cylindre sont marqués r. Le point où r touche le cylindre est marqué P. Une flèche étiquetée r qui provient de P et pointe vers l'extérieur sur la même ligne que r. — Figure\(\PageIndex{8}\) : Le champ électrique dans une situation de symétrie cylindrique dépend uniquement de la distance par rapport à l'axe. La direction du champ électrique est orientée à l'opposé de l'axe pour les charges positives et vers l'axe pour les charges négatives.

Calcul de la surface et du flux gaussiens

Pour tirer parti de la direction et de la dépendance fonctionnelle du champ électrique, nous choisissons une surface gaussienne fermée ayant la forme d'un cylindre ayant le même axe que l'axe de la distribution de charge. Le flux à travers cette surface de rayon s et de hauteur L est facile à calculer si nous divisons notre tâche en deux parties : (a) un flux à travers les extrémités plates et (b) un flux à travers la surface incurvée (Figure\(\PageIndex{9}\)).

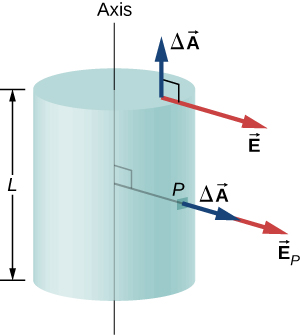
La figure montre un cylindre de longueur L. Une ligne perpendiculaire à l'axe relie l'axe au point P de la surface du cylindre. Une flèche nommée vecteur delta A pointe vers l'extérieur à partir de P dans la même direction que la ligne. Une autre flèche nommée vecteur E indice P provient de la pointe de la première flèche et pointe dans la même direction. Une troisième flèche nommée vecteur delta A pointe vers l'extérieur à partir de la surface supérieure du cylindre, perpendiculairement à celui-ci. Une flèche nommée vecteur E provient de la base de la troisième flèche et est perpendiculaire à celle-ci. — Figure\(\PageIndex{9}\) : La surface gaussienne dans le cas d'une symétrie cylindrique. Le champ électrique au niveau d'une plaque est soit parallèle soit perpendiculaire à la normale à la plaque de la surface gaussienne.

Le champ électrique est perpendiculaire au côté cylindrique et parallèle aux embouts plans de la surface. Le flux à travers la partie cylindrique est

\[\int_S \vec{E} \cdot \hat{n} dA = E \int_S dA = E(2\pi r L), \nonumber\]

alors que le flux à travers les embouts est nul car\(\vec{E} \cdot \hat{n} = 0\) là. Ainsi, le flux est

\[\int_S \vec{E} \cdot \hat{n} dA = E(2\pi rL) + 0 + 0 = 2\pi rLE. \nonumber\]

Utiliser la loi de Gauss

Selon la loi de Gauss, le flux doit être égal à la quantité de charge dans le volume délimité par cette surface, divisée par la permittivité de l'espace libre. Lorsque vous faites le calcul pour un cylindre de longueur L, vous constatez que\(q_{enc}\) la loi de Gauss est directement proportionnelle à L. Écrivons-le comme la charge par unité de longueur (\(\lambda_{enc}\)) multipliée par la longueur L :

\[q_{enc} = \lambda_{enc} L.\]

Ainsi, la loi de Gauss pour toute distribution de charge à symétrie cylindrique donne l'amplitude suivante du champ électrique à une distance s de l'axe :

\[Magnitude: \, E(r) = \dfrac{\lambda_{enc}}{2\pi \epsilon_0} \dfrac{1}{r}.\]

La charge par unité de longueur\(\lambda_{enc}\) dépend du fait que le point de champ se trouve à l'intérieur ou à l'extérieur du cylindre de distribution de charge, comme nous l'avons vu pour la distribution sphérique.

Charge informatique fermée

Soit R le rayon du cylindre à l'intérieur duquel les charges sont réparties de manière cylindrique symétrique. Soit le point de champ P à une distance s de l'axe. (Le côté de la surface gaussienne inclut le point de champ P.) Lorsque\(r > R\) (c'est-à-dire lorsque P est en dehors de la distribution de charge), la surface gaussienne inclut toute la charge dans le cylindre de rayon R et de longueur L. Lorsque\(r < R\) (P est situé à l'intérieur de la distribution de charge), seule la charge à l'intérieur d'un cylindre de rayon s et de longueur L est entourée par la surface gaussienne :

\(\lambda_{enc} = (total \, charge) \, if \, r \geq R\)

\(\lambda_{enc} = (only \, charge \, within \, t < R) \, if \, r < R\)

Coque cylindrique chargée uniformément

Une très longue coque cylindrique non conductrice de rayon R possède une densité de charge de surface uniforme\(\sigma_0\) Trouvez le champ électrique (a) en un point à l'extérieur de la coque et (b) en un point à l'intérieur de la coque.

Stratégie

Appliquez la stratégie juridique de Gauss exposée précédemment, selon laquelle nous traitons les affaires à l'intérieur et à l'extérieur de la coque séparément.

Solution

a. Champ électrique en un point situé à l'extérieur de la coque. Pour un point situé à l'extérieur de la coque cylindrique, la surface gaussienne est la surface d'un cylindre de rayon\(r > R\) et de longueur L, comme indiqué sur la figure\(\PageIndex{10}\). La charge enfermée par le cylindre gaussien est égale à la charge sur la coque cylindrique de longueur L. Par conséquent,\(\lambda_{enc}\) est donné par\[\lambda_{enc} = \dfrac{\sigma_0 2\pi RL}{L} = 2\pi R \sigma_0.\]

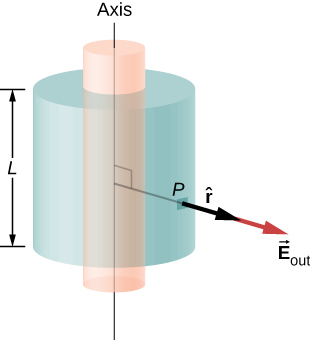
Deux cylindres partageant le même axe sont représentés. Le cylindre extérieur a une longueur L, qui est inférieure à la longueur du cylindre intérieur. Une ligne perpendiculaire à l'axe relie l'axe au point P sur la surface du cylindre extérieur. Une flèche étiquetée ou pointant vers l'extérieur à partir de P dans la même direction que la ligne. Une autre flèche nommée vecteur E en indice sortant provient de la pointe de la première flèche et pointe dans la même direction. — Figure\(\PageIndex{10}\) : Surface gaussienne entourant une coque cylindrique.

Par conséquent, le champ électrique en un point P à l'extérieur de la coque à une distance r de l'axe est

\[\vec{E} = \dfrac{2\pi R \sigma_0}{2 \pi \epsilon_0} \dfrac{1}{r} \hat{r} = \dfrac{R\sigma_0}{\epsilon_0} \dfrac{1}{r} \hat{r} \, (r > R)\]

où\(\hat{r}\) est un vecteur unitaire, perpendiculaire à l'axe et pointant à l'opposé de celui-ci, comme indiqué sur la figure. Le champ électrique en P pointe dans la direction\(\hat{r}\) indiquée sur la figure\(\PageIndex{10}\) if\(\sigma_0 > 0\) et dans la direction opposée à\(\hat{r}\) if\(\sigma_0 <0\).

b. Champ électrique en un point situé à l'intérieur de la coque. Pour un point situé à l'intérieur de la coque cylindrique, la surface gaussienne est un cylindre dont le rayon r est inférieur à R (Figure\(\PageIndex{11}\)). Cela signifie qu'aucune charge n'est incluse à l'intérieur de la surface gaussienne :

\[\lambda_{enc} = 0.\]

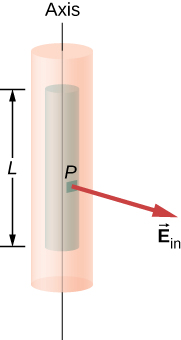
Deux cylindres partageant le même axe sont représentés. Le cylindre intérieur a une longueur L, qui est inférieure à la longueur du cylindre extérieur. Une flèche étiquetée E indice in provient d'un point P sur le cylindre intérieur et pointe vers l'extérieur, perpendiculairement à l'axe. — Figure\(\PageIndex{11}\) : Une surface gaussienne à l'intérieur d'une coque cylindrique.

On obtient ainsi l'équation suivante pour l'amplitude du champ électrique\(E_{in}\) en un point dont r est inférieur à R de la couche de charges.

\[E_{in} 2\pi rL = 0 (r<R), \nonumber\]

Cela nous donne

\[E_{in} = 0 (r < R). \nonumber\]

L'importance

Notez que le résultat à l'intérieur de la coque est exactement ce à quoi nous devrions nous attendre : aucune charge fermée signifie zéro champ électrique. En dehors de la coque, le résultat devient identique à celui d'un fil à charge uniforme\(R\sigma\).

Exercice\(\PageIndex{2}\)

Un fil droit fin possède une densité de charge linéaire uniforme\(\lambda_0\). Trouvez le champ électrique à une distance d du fil, où d est bien inférieur à la longueur du fil.

Solution

\(\vec{E} = \frac{\lambda_0}{2\pi \epsilon_0} \frac{1}{d} \hat{r}\); Cela concorde avec le calcul de [link] où nous avons trouvé le champ électrique en l'intégrant sur le fil chargé. Remarquez à quel point le calcul de ce champ électrique est beaucoup plus simple avec la loi de Gauss.

Distribution de charge avec symétrie planaire

Une symétrie plane de densité de charge est obtenue lorsque les charges sont réparties uniformément sur une grande surface plane. En symétrie planaire, tous les points d'un plan parallèle au plan de charge sont identiques par rapport aux charges.

Effets de la symétrie

Nous prenons le plan de la distribution de charge comme étant le plan xy et nous trouvons le champ électrique à un point spatial P avec des coordonnées (x, y, z). Comme la densité de charge est la même à toutes les coordonnées (x, y) du\(z = 0\) plan, par symétrie, le champ électrique à P ne peut pas dépendre des coordonnées x ou y du point P, comme le montre la figure\(\PageIndex{12}\). Par conséquent, le champ électrique en P ne peut dépendre que de la distance par rapport à l'avion et a une direction soit vers le plan, soit vers l'opposé de celui-ci. C'est-à-dire que le champ électrique en P n'a qu'une composante z non nulle.

Charges uniformes dans le plan xy :\(\vec{E} = E(z) \hat{z}\) où z est la distance par rapport au plan et\(\hat{z}\) le vecteur unitaire normal au plan. Notez que dans ce système, bien que\(E(z) = E(-z)\), bien sûr, ils pointent dans des directions opposées.

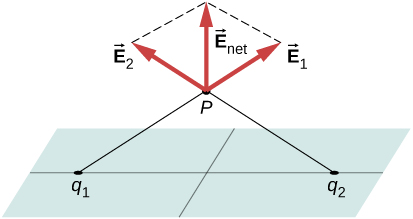
La figure montre un avion. Les points q1 et q2 se trouvent sur le plan, à égale distance de son centre. Des lignes relient ces points à un point P au-dessus du plan. Les flèches étiquetées vecteur E1 et vecteur E2 partent du point P et pointent dans des directions opposées aux lignes reliant P à q1 et q2 respectivement. Une troisième flèche partant de P coupe en deux l'angle formé par les deux premières flèches. Ceci est étiqueté vecteur E indice net. — Figure\(\PageIndex{12}\) : Les composantes du champ électrique parallèles à un plan de charges annulent les deux charges situées symétriquement à partir du point de champ P. Par conséquent, le champ en tout point est pointé verticalement à partir du plan des charges. Pour n'importe quel point P et charge\(q_1\), on peut toujours trouver un\(q_2\) avec cet effet.

Calcul de la surface et du flux gaussiens

Dans le cas présent, une surface gaussienne appropriée est une boîte, puisque le champ électrique attendu ne pointe que dans une seule direction. Pour maintenir la boîte de Gauss symétrique par rapport au plan des charges, nous la prenons pour chevaucher le plan des charges, de telle sorte qu'une face contenant le point de champ P soit prise parallèlement au plan des charges. Sur la figure\(\PageIndex{13}\), les côtés I et II de la surface gaussienne (la boîte) qui sont parallèles au plan infini ont été ombrés. Ce sont les seules surfaces qui génèrent un flux non nul car le champ électrique et les vecteurs de surface des autres faces sont perpendiculaires l'un à l'autre.

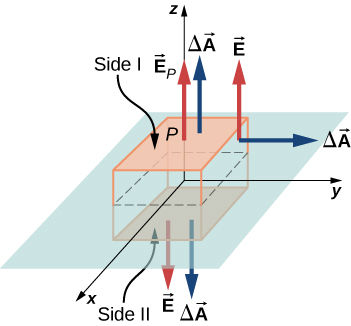
La figure montre un cuboïde et un plan passant par son centre. Les surfaces supérieure et inférieure du cuboïde sont parallèles au plan et sont étiquetées Diapositive 1 et Diapositive 2 respectivement. Une flèche nommée vecteur E indice P provient du point P situé au centre de la surface supérieure et pointe vers le haut, perpendiculairement à la surface. Une autre flèche nommée vecteur delta A pointe également vers le haut à partir de la surface supérieure. Deux flèches étiquetées vecteur E et vecteur delta A pointent vers le bas à partir de la surface inférieure. Un vecteur delta de flèche A provient de la surface droite et pointe vers l'extérieur, perpendiculairement à la surface. Une autre flèche part de sa base. Il est étiqueté vecteur E et pointe vers le haut. — Figure\(\PageIndex{13}\) : Une fine feuille chargée et la boîte gaussienne permettant de déterminer le champ électrique au point de champ P. La normale de chaque face de la boîte va de l'intérieur de la boîte vers l'extérieur. Sur deux faces de la boîte, les champs électriques sont parallèles aux vecteurs de surface, et sur les quatre autres faces, les champs électriques sont perpendiculaires aux vecteurs de surface.

Soit A la zone de la surface ombrée de chaque côté du plan et E P

être l'amplitude du champ électrique au point P. Comme les côtés I et II se trouvent à la même distance du plan, le champ électrique a la même intensité en certains points de ces plans, bien que les directions du champ électrique à ces points des deux plans soient opposées l'une à l'autre.

Magnitude en I ou II :\(E(z) = E_p\).

Si la charge sur le plan est positive, la direction du champ électrique et les vecteurs de surface sont tels que présentés sur la figure\(\PageIndex{13}\). Par conséquent, nous trouvons le flux de champ électrique à travers la boîte

\[\Phi = \int_S \vec{E}_p \cdot \hat{n} dA = E_pA + E_pA + 0 + 0 + 0 + 0 = 2E_p A\]

où les zéros correspondent au flux traversant les autres côtés de la boîte. Notez que si la charge sur le plan est négative, les directions du champ électrique et les vecteurs de surface pour les plans I et II sont opposés l'un à l'autre, et nous obtenons un signe négatif pour le flux. Selon la loi de Gauss, le flux doit être égal\(q_{enc}/\epsilon_0\). Sur la figure\(\PageIndex{13}\), nous voyons que les charges à l'intérieur du volume délimité par la boîte gaussienne résident sur une zone A du plan xy. Par conséquent,

\[q_{enc} = \sigma_0 A. \nonumber\]

En utilisant les équations du flux et de la charge incluse dans la loi de Gauss, nous pouvons déterminer immédiatement le champ électrique en un point situé à la hauteur z à partir d'un plan uniformément chargé dans le plan xy :

\[\vec{E}_p = \dfrac{\sigma_0}{2\epsilon_0} \hat{n}. \nonumber\]

La direction du champ dépend du signe de la charge sur le plan et du côté du plan où se trouve le point de champ P. Notez qu'au-dessus de l'avion\(\hat{n} = + \hat{z}\), tandis qu'en dessous de l'avion,\(\hat{n} = - \hat{z}\).

Vous serez peut-être surpris de constater que le champ électrique ne dépend pas réellement de la distance par rapport à l'avion ; c'est un effet de l'hypothèse que le plan est infini. Concrètement, le résultat donné ci-dessus reste une approximation utile pour les plans finis proches du centre.