7.A : Mécanique quantique (réponses)

Vérifiez votre compréhension

7.1. \(\displaystyle (3+4i)(3−4i)=9−16i^2=25\)

7.2. \(\displaystyle A=\sqrt{2/L}\)

7.3. \(\displaystyle (1/2−1/π)/2=9%\)

7.4. \(\displaystyle 4.1×10^{−8}eV; 1.1×10^{−5}nm\)

7.5. \(\displaystyle 0.5mω^2x^2ψ(x)∗ψ(x)\)

7.6. Aucune. La première fonction présente une discontinuité, la deuxième est à double valeur et la troisième fonction diverge et n'est donc pas normalisable.

7.7. a. 9,1 % ;

b. 25 %

7.8. environ 295 N/m ;

b. 0,277 eV

7.9. \(\displaystyle ⟨x⟩=0\)

7.10. \(\displaystyle L_{proton}/L_{electron}=\sqrt{m_e/m_p}=2.3%\)

Questions conceptuelles

1. \(\displaystyle 1/\sqrt{L}\), où\(\displaystyle L=length\) ; 1/L, où\(\displaystyle L=length\)

3. La fonction d'onde ne correspond directement à aucune quantité mesurée. Il s'agit d'un outil permettant de prédire les valeurs des grandeurs physiques.

5. La valeur moyenne de la quantité physique pour un grand nombre de particules ayant la même fonction d'onde.

7. Oui, si sa position est totalement inconnue. Oui, si son élan est totalement inconnu.

9. Non. Selon le principe d'incertitude, si l'incertitude sur la position de la particule est faible, l'incertitude sur sa quantité de mouvement est grande. De même, si l'incertitude sur la position de la particule est grande, l'incertitude sur sa quantité de mouvement est faible.

11. Non, cela signifie que les prédictions concernant la particule (exprimées en termes de probabilités) sont indépendantes du temps.

13. Non, car la probabilité que la particule existe dans un intervalle étroit (infinitésimalement petit) au moment de la discontinuité n'est pas définie.

15. Non. Pour un puits carré infini, l'espacement entre les niveaux d'énergie augmente avec le nombre quantique n. La plus petite énergie mesurée correspond à la transition de n = 2 à 1, soit trois fois l'énergie de l'état fondamental. La plus grande énergie mesurée correspond à une transition de\(\displaystyle n=∞\) à 1, qui est l'infini. (Remarque : même les particules aux énergies extrêmement importantes restent liées à un puits carré infini ; elles ne peuvent jamais « s'échapper »)

17. Non. Cette énergie correspond à\(\displaystyle n=0.25\), mais n doit être un entier.

19. Parce que la plus petite valeur autorisée du nombre quantique n pour un oscillateur harmonique simple est 0. Non, parce que la mécanique quantique et la mécanique classique ne s'accordent que dans la limite d'un grand nn.

21. Oui, dans les limites du principe d'incertitude. Si la particule oscillante est localisée, la quantité de mouvement et donc l'énergie de l'oscillateur sont distribuées.

23. doubler la largeur de la barrière

25. Non, la force de rappel exercée sur la particule aux parois d'un puits carré infini est infinie.

Problèmes

27. \(\displaystyle ∣ψ(x)∣^2sin^2ωt\)

29. (a) et (e), peuvent être normalisés

31. un\(\displaystyle A=\sqrt{2α/π}\) ;.

b.\(\displaystyle probability=29.3%\) ;

c.\(\displaystyle ⟨x⟩=0⟨x⟩=0\) ;.

d\(\displaystyle ⟨p⟩=0\) ;.

e.\(\displaystyle ⟨K⟩=α^2ℏ^2/2m\)

33. un\(\displaystyle Δp≥2.11×10^{−34}N⋅s\) ;.

b.\(\displaystyle Δv≥6.31×10^{−8}m\) ;

c.\(\displaystyle Δv/\sqrt{k_BT/m_α}=5.94×10^{−11}\)

35. \(\displaystyle Δτ≥1.6×10^{−25}s\)

37. un\(\displaystyle Δf≥1.59MHz\) ;.

b.\(\displaystyle Δω/ω_0=3.135×10^{−9}\)

39. Réaliser les rendements des dérivés\(\displaystyle k^2=\frac{ω^2}{c^2}\).

41. L'exécution des dérivées (comme ci-dessus) pour la fonction sinusoïdale donne un cosinus sur le côté droit de l'équation, de sorte que l'égalité échoue. Il en va de même pour la solution de cosinus.

43. \(\displaystyle E=ℏ^2k^2/2m\)

45. \(\displaystyle ℏ^2k^2ℏ\); La particule a un moment défini et donc un moment défini au carré.

47. 9,4 eV, 64 %

49. 0,38 nm

51. 1,82 MeV

53. 24,7 nm

55. \(\displaystyle 6.03Å\)

57. un.

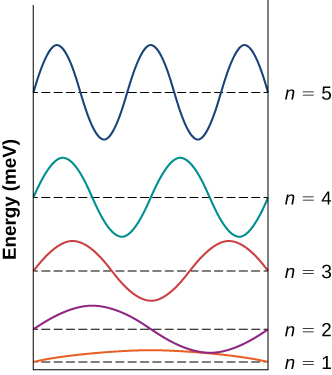
Les fonctions d'onde pour les états n = 1 à n = 5 de l'électron dans un puits carré infini sont présentées. Chaque fonction est déplacée verticalement par son énergie, mesurée en MeV. L'état n=1 est la première demi-onde de la fonction sinusoïdale. La fonction n=2 est la première onde complète de la fonction sinusoïdale. La fonction n=3 est la première onde et demie de la fonction sinusoïdale. La fonction n=4 correspond aux deux premières ondes de la fonction sinusoïdale. La fonction n=5 correspond aux deux premières ondes et demie de la fonction sinusoïdale. ;

b.\(\displaystyle λ_{5→3}=12.9nm,λ_{3→1}=25.8nm,λ_{4→3}=29.4nm\)

59. preuve

61. \(\displaystyle 6.662×10^{14}Hz\)

63. \(\displaystyle n≈2.037×10^{30}\)

65. \(\displaystyle ⟨x⟩=0.5mω^2⟨x^2⟩=ℏω/4\);\(\displaystyle ⟨K⟩=⟨E⟩−⟨U⟩=ℏω/4\)

67. preuve

69. Une fonction complexe de la forme\(\displaystyle Ae^{iϕ}\), satisfait l'équation indépendante du temps de Schrdinger. Les opérateurs de l'énergie cinétique et de l'énergie totale étant linéaires, toute combinaison linéaire de telles fonctions d'onde constitue également une solution valide à l'équation de SchrDinger. Nous concluons donc que l'équation 7.68 satisfait l'équation 7.61 et que l'équation 7.69 satisfait l'équation 7.63.

71. a. 4,21 % ;

b. 0,84 % ;

environ 0,06 %

73. a. 0,13 % ;

b. près de 0 %

75. 0,38 nm

Problèmes supplémentaires

77. preuve

79. a. 4,0 % ;

b. 1,4 % ;

c. 4,0 % ;

d. 1,4 %

81. un\(\displaystyle t=mL^2/h=2.15×10^{26}years\) ;.

b.\(\displaystyle E_1=1.46×10^{−66}J,K=0.4J\)

83. preuve

85. 1,2 N/m

87. 0

Problèmes liés au défi

89. 19,2 µm ; 11,5 µm 19,2 µm ; 11,5 µm

91. 3,92 %

93. preuve