7.7 : Tunnellisation quantique de particules à travers des barrières potentielles
- Page ID
- 189870
À la fin de cette section, vous serez en mesure de :
- Décrire comment une particule quantique peut traverser une barrière potentielle
- Identifier les paramètres physiques importants qui influent sur la probabilité de creusement d'un tunnel
- Identifier les phénomènes physiques dans lesquels le tunneling quantique est observé
- Expliquer comment le tunneling quantique est utilisé dans les technologies modernes
Le tunneling quantique est un phénomène par lequel des particules pénètrent une barrière énergétique potentielle d'une hauteur supérieure à l'énergie totale des particules. Le phénomène est intéressant et important car il viole les principes de la mécanique classique. Le tunneling quantique est important dans les modèles du Soleil et possède un large éventail d'applications, telles que le microscope à effet tunnel à balayage et la diode tunnel.
Creusement de tunnels et énergie potentielle
Pour illustrer le tunneling quantique, imaginez une balle roulant le long d'une surface avec une énergie cinétique de 100 J. Lorsque la balle roule, elle rencontre une colline. L'énergie potentielle de la balle placée au sommet de la colline est de 10 J. Par conséquent, la balle (avec 100 J d'énergie cinétique) roule facilement sur la colline et continue. En mécanique classique, la probabilité que la balle passe au-dessus de la colline est exactement de 1 à chaque fois. Si, toutefois, la hauteur de la colline augmente (une balle placée au sommet de la colline a une énergie potentielle de 200 J), la balle ne remonte qu'une partie de la colline, s'arrête et revient dans la direction dans laquelle elle est venue. L'énergie totale de la balle est entièrement convertie en énergie potentielle avant qu'elle n'atteigne le sommet de la colline. Nous ne nous attendons pas à ce que, même après des tentatives répétées, la balle de 100 J soit trouvée au-delà de la colline. Par conséquent, la probabilité que la balle passe au-dessus de la colline est exactement de 0, et la probabilité qu'elle soit retournée ou « réfléchie » par la colline est exactement de 1. Le ballon ne franchit jamais la colline. L'existence de la balle au-delà de la colline est impossible ou « interdite sur le plan énergétique ».
Cependant, selon la mécanique quantique, la balle a une fonction ondulatoire et cette fonction est définie dans tout l'espace. La fonction ondulatoire peut être très localisée, mais il est toujours possible que lorsque la balle entre en contact avec la colline, elle se retrouve soudainement au-delà de celle-ci. En effet, cette probabilité est appréciable si le « paquet d'ondes » de la balle est plus large que la barrière.
Regardez cette simulation interactive pour une simulation du creusement de tunnels.
Dans le langage de la mécanique quantique, la colline est caractérisée par une barrière potentielle. Une barrière carrée de hauteur finie est décrite par la fonction d'énergie potentielle suivante :
\ [U (x) =
\ begin {cas}
0, & \ mbox {quand} x < 0 \ \ [4pt] U_0, & \ mbox {when} 0 \ leq x \ leq L \ \ [4pt] 0, & \ mbox {when} x > L
\ end {cas} \ label {PIBPotential} \]
L'obstacle potentiel est illustré dans la figure\(\PageIndex{1}\). Lorsque la hauteur\(U_0\) de la barrière est infinie, le paquet d'ondes représentant une particule quantique incidente est incapable de la pénétrer, et la particule quantique rebondit à partir de la limite de la barrière, comme une particule classique. Lorsque la largeur\(L\) de la barrière est infinie et que sa hauteur est finie, une partie du paquet d'ondes représentant une particule quantique incidente peut filtrer à travers la limite de la barrière et éventuellement périr après avoir parcouru une certaine distance à l'intérieur de la barrière.
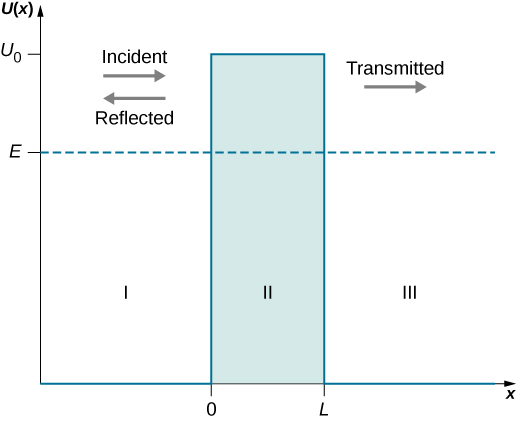
Lorsque la largeur\(L\) et la hauteur\(U_0\) sont toutes deux finies, une partie du paquet d'ondes quantiques incident d'un côté de la barrière peut pénétrer la limite de la barrière et poursuivre son mouvement à l'intérieur de la barrière, où elle est progressivement atténuée en se dirigeant vers l'autre côté. Une partie du paquet d'ondes quantiques incident émerge finalement de l'autre côté de la barrière sous la forme du paquet d'ondes transmis qui a traversé la barrière par tunnel. La part de l'onde incidente qui peut traverser une barrière dépend de la largeur\(L\) et de la hauteur de la barrière\(U_0\), ainsi que de l'énergie\(E\) de la particule quantique incidente sur la barrière. C'est la physique du creusement de tunnels.
La pénétration de la barrière par les fonctions d'ondes quantiques a été analysée pour la première fois théoriquement par Friedrich Hund en 1927, peu après que Schrdinger ait publié l'équation qui porte son nom. Un an plus tard, George Gamow a utilisé le formalisme de la mécanique quantique pour expliquer la\(\alpha\) désintégration radioactive des noyaux atomiques en tant que phénomène de tunnel quantique. L'invention de la diode tunnel en 1957 a clairement montré que le tunneling quantique est important pour l'industrie des semi-conducteurs. Dans les nanotechnologies modernes, les atomes individuels sont manipulés à l'aide de connaissances en tunnel quantique.
Le tunneling et la fonction Wave
Supposons qu'un faisceau uniforme et indépendant du temps d'électrons ou d'autres particules quantiques dont l'énergie\(E\) se déplace le long de l'axe x (dans la direction positive vers la droite) rencontre une barrière de potentiel décrite par l'équation \ ref {PIBPotential}. La question est la suivante : quelle est la probabilité qu'une particule individuelle du faisceau traverse la barrière potentielle ? La réponse peut être trouvée en résolvant le problème des valeurs limites de l'équation de SchrDinger indépendante du temps pour une particule dans le faisceau. La forme générale de cette équation est donnée par l'équation \ ref {TISE}, que nous reproduisons ici :
\[-\frac{\hbar^2}{2m} \frac{d^2\psi(x)}{dx^2} + U(x)\psi(x) = E\psi(x), \label{TISE} \]
où\(-\infty < x < +\infty\).
La fonction potentielle\(U(x)\) dans l'équation \ ref {TISE} est définie par l'équation \ ref {PIBPotential}. Nous supposons que l'énergie donnée\(E\) de la particule entrante est inférieure à la hauteur\(U_0\) de la barrière de potentiel\(E < U_0\), car c'est un cas physique intéressant. Connaissant l'énergie\(E\) de la particule entrante, notre tâche consiste à résoudre l'équation \ ref {TISE} pour une fonction\(\psi(x)\) continue et ayant des dérivées premières continues pour tous les x. En d'autres termes, nous recherchons une solution « lisse » (parce que c'est à cela que ressemblent les fonctions d'onde) qui puisse faire l'objet d'une interprétation probabiliste,\(|\psi(x)|^2 = \psi^*(x)\psi(x)\) c'est-à-dire la densité de probabilité.
Nous divisons l'axe réel en trois régions avec les limites définies par la fonction potentielle dans l'équation \ ref {PIBPotential} (illustrée dans la figure\(\PageIndex{1}\)) et nous transcrivons l'équation \ ref {TISE} pour chaque région. Dénotée par\(\psi_I(x)\) la solution dans la région\(I\) pour\(x < 0\), par\(\psi_{II}(x)\) la solution dans la région\(II\) pour\(0 \leq x \leq L\) et par\(\psi_{III}(x)\) la solution dans la région\(III\) pour\(x > L\), l'équation de Schrdinger stationnaire a les formes suivantes dans ces trois régions :
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_I(x)}{dx^2} = E\psi_I(x), \label{R1} \]
dans la région\(I\) :\(-\infty < x < 0,\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_{II}(x)}{dx^2} + U_0\psi_{II}(x) = E\psi_{II}(x) \label{R2} \]
dans la région\(II\) :\(0 < x < L,\)
\[-\dfrac{\hbar^2}{2m} \frac{d^2\psi_{III}(x)}{dx^2} = E\psi_{III}(x) \label{R3} \]
dans la région\(III\) :\(L < x < +\infty,\)
La condition de continuité aux limites des régions exige que :
\[\psi_I(0) = \psi_{II}(0) \label{Bound1} \]
à la frontière entre les régions\(I\) et\(II\)
et
\[\psi_{II}(L) = \psi_{III}(L) \label{Bound2} \]
à la frontière entre les régions\(II\) et\(III\).
La condition de « douceur » exige que la dérivée première de la solution soit continue aux limites des régions :
\[ \left.\dfrac{d\psi_I(x)}{dx}\right|_{x = 0} = \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = 0} \label{smooth1} \]
à la frontière entre les régions\(I\) et\(II\)
et
\[ \left.\dfrac{d\psi_{II}(x)}{dx}\right|_{x = L} = \left.\dfrac{d\psi_{III}(x)}{dx}\right|_{x = L} \label{smooth2} \]
à la frontière entre les régions\(II\) et\(III\).
Dans ce qui suit, nous trouvons les fonctions\(\psi_I(x), \, \psi_{II}(x)\), et\(\psi_{III}(x)\).
Nous pouvons facilement vérifier (en les remplaçant dans l'équation d'origine et en les différenciant) que, dans les régions\(I\) et\(III\), les solutions doivent se présenter sous les formes générales suivantes :
\[\psi_I(x) = Ae^{+ikx} + Be^{-ikx} \label{Eq5A} \]
\[\psi_{III}(x) = Fe^{+ikx} + Ge^{-ikx} \label{Eq5B} \]
où\(k = \sqrt{2mE}/\hbar\) est un nombre d'onde et où l'exposant complexe indique des oscillations,
\[e^{\pm ikx} = \cos \, kx \pm i \, \sin \, kx. \nonumber \]
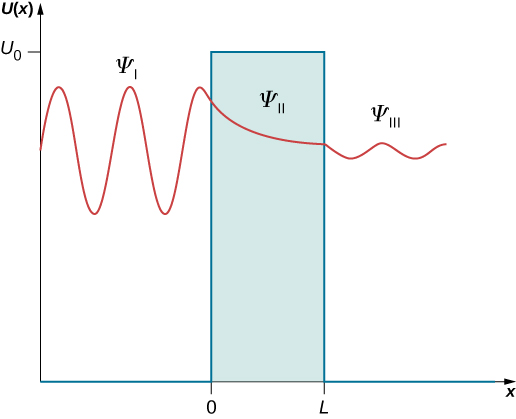
Les constantes\(A\),\(B\)\(F\), et\(G\) dans les équations \ ref {Eq5A} et \ ref {Eq5B} peuvent être complexes. Ces solutions sont illustrées dans la figure\(\PageIndex{2}\). Dans la région I, il y a deux ondes, l'une incidente (se déplaçant vers la droite) et l'autre réfléchie (se déplaçant vers la gauche), de sorte qu'aucune des constantes\(A\) et\(B\) dans l'équation \ ref {Eq5A} ne peut disparaître. Dans la région III, il n'y a qu'une seule onde (se déplaçant vers la droite), qui est l'onde émise, donc la constante\(G\) doit être nulle dans l'équation \ ref {Eq5B},\(G = 0\). Nous pouvons écrire explicitement que l'onde incidente est\(\psi_{in}(x) = Ae^{+ikx}\) et que l'onde réfléchie l'est\(\psi_{ref}(x) = Be^{-ikx}\), et que l'onde émise l'est\(\psi_{tra}(x) = Fe^{+ikx}\). L'amplitude de l'onde incidente est
\[ \begin{align*}|\psi_{in}(x)|^2 &= \psi_{in}^*(x)\psi_{in}(x) \\[4pt] &= (Ae^{+ikx})^*Ae^{+ikx} \\[4pt] &= A^*e^{-ikx}Ae^{+ikx} \\[4pt] &= A^*A = |A|^2. \end{align*} \nonumber \]
De même, l'amplitude de l'onde réfléchie est\(|\psi_{ref}(x)|^2 = |B|^2\) et l'amplitude de l'onde émise est\(|\psi_{tra}(x)|^2 = |F|^2\). La théorie des ondes nous apprend que le carré de l'amplitude de l'onde est directement proportionnel à l'intensité de l'onde. Si nous voulons connaître la part de l'onde incidente qui traverse la barrière, nous devons calculer le carré de l'amplitude de l'onde émise. La probabilité de transmission ou probabilité de tunnel est le rapport entre l'intensité émise (\(|F|^2\)) et l'intensité incidente (\(|A|^2\)), écrit comme
\[ \begin{align} T(L, E) &= \frac{|\psi_{tra}(x)|^2}{|\psi_{in}(x)|^2} \\[4pt] &= \frac{|F|^2}{|A|^2} \\[4pt] &= \left|\frac{F}{A}\right|^2 \label{trans} \end{align} \]
où\(L\) est la largeur de la barrière et\(E\) l'énergie totale de la particule. Il s'agit de la probabilité qu'une particule individuelle du faisceau incident traverse la barrière potentielle. Intuitivement, nous comprenons que cette probabilité doit dépendre de la hauteur de la barrière\(U_0\).
Dans la région II, les termes de l'équation Equation \ ref {R2} peuvent être réorganisés comme suit :
\[\frac{d^2\psi_{II}(x)}{dx^2} = \beta^2 \psi_{II}(x) \label{eq10} \]
où\(\beta^2\) est positif car\(U_0 > E\) et le paramètre\(\beta\) est un nombre réel,
\[\beta^2 = \frac{2m}{\hbar^2}(U_0 - E). \label{eq20} \]
La solution générale de l'équation \ ref {eq10} n'est pas oscillatoire (contrairement aux autres régions) et se présente sous la forme d'exponentielles qui décrivent une atténuation progressive de\(\psi_{II}(x)\),
\[\psi_{II}(x) = Ce^{-\beta x} + De^{+\beta x}. \label{eq25B} \]
Les deux types de solutions dans les trois régions sont illustrés dans la figure\(\PageIndex{2}\).
Nous utilisons maintenant les conditions limites pour trouver des équations pour les constantes inconnues. Les équations \ ref {Eq5A} et \ ref {EQ25b} sont substituées dans l'équation \ ref {Bound1} pour donner
\[A + B = C + D. \nonumber \]
Les équations \ ref {EQ25b} et \ ref {Eq5B} sont substituées dans l'équation \ ref {Bound2} pour donner
\[Ce^{-\beta L} + De^{+\beta L} = Fe^{+ik L}. \nonumber \]
De même, nous substituons les équations \ ref {Eq5A} et \ ref {EQ25b} par l'équation \ ref {smooth1}, différencions et obtenons
\[-ik(A - B) = \beta(D - C). \nonumber \]
De même, la condition limite Equation \ ref {smooth2} se lit explicitement
\[\beta (De^{+\beta L} - Ce^{-\beta L}) = +ikFe^{+ikL}. \nonumber \]
Nous avons maintenant quatre équations pour cinq constantes inconnues. Cependant, comme la quantité que nous recherchons est le coefficient de transmission (\(T\)), défini dans l'équation \ ref {trans} par la fraction\(F/A\), le nombre d'équations est exactement correct car lorsque nous divisons chacune des équations ci-dessus par\(A\), nous n'avons que quatre fractions inconnues : \(B/A\),\(C/A\)\(D/A\), et\(F/A\), dont trois peuvent être éliminés pour être trouvés\(F/A\). L'algèbre proprement dite qui conduit à l'expression de\(F/A\) est assez longue, mais elle peut être réalisée à la main ou à l'aide d'un logiciel informatique. Le résultat final est
\[\frac{F}{A} = \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}. \label{eq40} \]
Pour dériver l'équation \ ref {eq40}, pour éviter tout désordre, nous utilisons les substitutions\(\gamma \equiv \beta/k - k/\beta\) et la définition des fonctions hyperboliques :
\[\cosh \, y = \frac{e^y + e^{-y}}{2} \nonumber \]
et
\[\sinh \, y = \frac{e^y - e^{-y}}{2}. \nonumber \]
Nous remplaçons l'équation \ ref {eq40} par l'équation \ ref {trans} et obtenons l'expression exacte du coefficient de transmission de la barrière,
\[T(L,E) = \left(\frac{F}{A}\right)^*\frac{F}{A} = \frac{e^{+ikL}}{\cosh \, (\beta L) - i (\gamma /2) \, \sinh \, (\beta L)} \cdot \frac{e^{-ikL}}{\cosh \, (\beta L) + i (\gamma /2) \, \sinh \, (\beta L)}. \nonumber \]
ou
\[T(L,E) = \frac{1}{\cosh^2 \, (\beta L) + (\gamma /2)^2 \, \sinh^2 \, (\beta L)}. \label{eqTrans1} \]
où
\[\left(\frac{\gamma}{2}\right)^2 = \frac{1}{4}\left( \frac{1 - E/U_0}{E/U_0} + \frac{E/U_0}{1 - E/U_0} - 2\right). \nonumber \]
Pour une barrière large et haute qui transmet mal, l'équation \ ref {EQTrans1} peut être approximée par
\[T(L,E) \approx 16 \frac{E}{U_0}\left(1 - \dfrac{E}{U_0}\right) e^{-2\beta L}. \label{eqTrans2} \]
Qu'il s'agisse de l'expression exacte (Équation \ ref {EQTrans1}) ou de l'expression approximative (Équation \ ref {EQTrans2}), nous voyons que l'effet tunnel dépend très fortement de la largeur\(L\) de la barrière potentielle. En laboratoire, nous pouvons ajuster à la fois la hauteur\(U_0\) et la largeur potentielles\(L\) pour concevoir des nano-dispositifs avec des coefficients de transmission souhaitables.
Deux nanofils de cuivre sont isolés par une nano-couche d'oxyde de cuivre qui fournit une barrière de potentiel de 10,0 eV. Estimez la probabilité de création d'un tunnel entre les nanofils par des électrons de 7,00 eV à travers une couche d'oxyde de 5,00 nm d'épaisseur. Et si l'épaisseur de la couche était réduite à seulement 1,00 nm ? Et si l'énergie des électrons était augmentée à 9,00 eV ?
Stratégie
En traitant la couche d'oxyde isolante comme une barrière potentielle de hauteur finie, nous utilisons l'équation \ ref {EQTrans2}. Nous identifions\(U_0 = 10.0 \, eV, \, E_1 = 7.00 \, eV, \, E_2 = 9.00 \, eV, \, L_1 = 5.00 \, nm\), et\(L_2 = 1.00 \, nm\). Nous utilisons l'équation \ ref {eq20} pour calculer l'exposant. Nous avons également besoin de la masse restante de l'électron\(m = 511 \, keV/c^2\) et de la constante de Planck\(\hbar = 0.1973 \, keV \cdot nm/c\). Il est courant que ce type d'estimation porte sur de très petites quantités qui ne sont souvent pas adaptées aux calculatrices portatives. Pour effectuer des estimations correctes des commandes, nous effectuons la conversion\(e^y = 10^{y/ln \, 10}\).
Solution
Constantes :
\[\frac{2m}{\hbar^2} = \frac{2(511 \, keV/c^2)}{(0.1973 \, keV \cdot nm/c^2)^2} = 26,254 \frac{1}{keV \cdot (nm)^2}, \nonumber \]
\[\beta = \sqrt{\frac{2m}{\hbar^2}(U_0 - E)} = \sqrt{26,254\frac{(10.0 \, eV - E)}{keV \cdot (nm)^2}} = \sqrt{26.254(10.00 - E)/eV} \frac{1}{nm}.\nonumber \]
Pour un électron de faible énergie avec\(E_1 = 7.00 \, eV\) :
\[\beta_1 = \sqrt{26.254(10.00 \, eV - E_1)/eV}\frac{1}{nm} = \sqrt{26.254(10.00 - 7.00)}\frac{1}{nm} = \frac{8.875}{nm},\nonumber \]
\[T(L,E) = 16\frac{E_1}{U_0}\left(1 - \frac{E_1}{U_0}\right)e^{-2\beta_1L} = 16\frac{7}{10}\left(1 - \frac{7}{10}\right)e^{-17.75 \, L/nm} = 3.36 \, e^{-17.75 \, L/nm}\nonumber \]
Pour un électron de plus haute énergie avec\(E_2 = 9.00 \, eV\) :
\[\beta_2 = \sqrt{26.254(10.00 \, eV - E_2)/eV}\frac{1}{nm} = \sqrt{26.254 (10.00 - 9.00)}\frac{1}{nm} = \frac{5.124}{nm},\nonumber \]
\[T(L,E_2) = 16\frac{E_2}{U_0}\left( 1 - \frac{E_2}{U_0}\right) e^{-2\beta_2 L} = 16 \frac{9}{10} \left(1 - \frac{9}{10}\right) e^{-10.25 \, L/nm} = 1.44 \, e^{-10.25 \, L/nm}\nonumber \]
Pour une barrière large avec\(L_1 = 5.00 \, nm\) :
\[T(L_1,E_1) = 3.36 e^{-17.75 \, L_1/nm} = 3.36 e^{-17.75 \cdot 5.00 nm/nm} = 3.36e^{-88} = 3.36(6.2 \times 10^{-39}) = 2.1\% \times 10^{-36}\nonumber \]
\[T(L_1,E_2) = 1.44 e^{-10.25 \, L_1/nm} = 1.44 e^{-10.25 \cdot 5.00 \, nm/nm} = 1.44^{-51.2} = 1.44(5.81 \times 10^{-12}) = 8.36\% \times 10^{-25}\nonumber \]
Pour une barrière plus étroite avec\(L_2 = 1.00 \, nm\) :
\[T(L_2,E_1) = 3.36e^{−17.75 \, L_2/nm} = 3.36 e^{−17.75 \cdot 1.00 \, nm/nm} = 3.36 e^{−17.75} = 3.36(5.1 \times 10^{−7}) = 1.7\% \times 10^{−4},\nonumber \]
\[T(L_2,E_2) = 1.44e^{−10.25 \, L_2/nm} = 1.44e^{-10.25 \cdot 1.00 \, nm/nm} = 1.44e^{−10.25} = 1.44(3.53 \times 10^{−5}) = 5.09\% \times 10^{-7}.\nonumber \]
L'importance
Ces estimations montrent que la probabilité de creusement d'un tunnel dépend davantage de la largeur de la barrière potentielle que de l'énergie d'une particule incidente. Dans les technologies actuelles, nous pouvons manipuler des atomes individuels sur des surfaces métalliques afin de créer des barrières potentielles d'une fraction de nanomètre, donnant naissance à des courants tunnel mesurables. L'une des nombreuses applications de cette technologie est le microscope à effet tunnel à balayage (STM), dont nous parlerons plus loin dans cette section.
Un proton d'énergie cinétique de 1,00 eV est incident sur une barrière de potentiel carrée d'une hauteur de 10,00 eV. Si le proton doit avoir la même probabilité de transmission qu'un électron de même énergie, quelle doit être la largeur de la barrière par rapport à la largeur de barrière rencontrée par un électron ?
- Réponse
-
\[L_{proton}/L_{electron} = \sqrt{m_e/m_p} = 2.3\% \nonumber \]
Désintégration radioactive
En 1928, Gamow a identifié le tunnel quantique comme le mécanisme responsable de la désintégration radioactive des noyaux atomiques. Il a observé que certains isotopes du thorium, de l'uranium et du bismuth se désintègrent en émettant des particules α (qui sont des atomes d'hélium doublement ionisés ou, simplement, des noyaux d'hélium). Au cours du processus d'émission d'une particule α, le noyau d'origine est transformé en un nouveau noyau qui contient deux neutrons et deux protons de moins que le noyau d'origine. Les particules α émises par un isotope ont à peu près les mêmes énergies cinétiques. Lorsque nous examinons les variations de ces énergies entre les isotopes de divers éléments, l'énergie cinétique la plus faible est d'environ 4 MeV et la plus élevée d'environ 9 MeV, de sorte que ces énergies sont du même ordre de grandeur. C'est à peu près là que s'arrêtent les similitudes entre les différents isotopes.
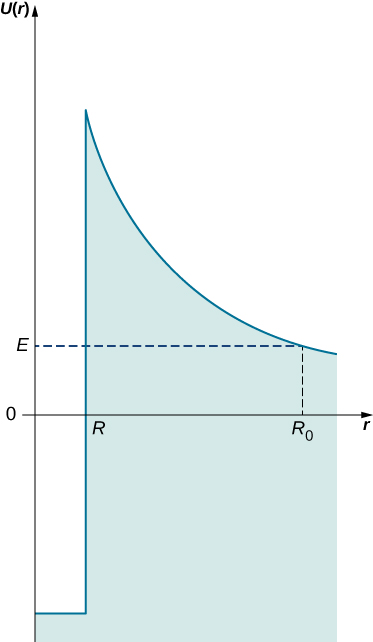
Lorsque nous inspectons les demi-vies (une demi-vie est la période pendant laquelle un échantillon radioactif perd la moitié de ses noyaux en raison de la désintégration), les différents isotopes diffèrent considérablement. Par exemple, la demi-vie du polonium-214 est de 160 µs et celle de l'uranium est de 4,5 milliards d'années. Gamow a expliqué cette variation en considérant un modèle de « boîte sphérique » du noyau, dans lequel les particules α peuvent rebondir entre les parois sous forme de particules libres. Le confinement est assuré par un fort potentiel nucléaire au niveau d'une paroi sphérique du boîtier. L'épaisseur de cette paroi n'est cependant pas infinie mais limitée, de sorte qu'en principe, une particule nucléaire a une chance d'échapper à ce confinement nucléaire. Sur la paroi intérieure de la barrière de confinement se trouve un potentiel nucléaire élevé qui maintient la particule α dans un petit confinement. Mais lorsqu'une particule α sort de l'autre côté de cette paroi, elle est soumise à une répulsion électrostatique de Coulomb et s'éloigne du noyau. Cette idée est illustrée dans la figure\(\PageIndex{3}\). La largeur\(L\) de la barrière de potentiel qui sépare une particule α du monde extérieur dépend de l'énergie cinétique de la particule\(E\). Cette largeur est la distance entre le point marqué par le rayon nucléaire\(R\) et le point\(R_0\) où une particule α émerge de l'autre côté de la barrière,\(L = R_0 - R\). À distance\(R_0\), son énergie cinétique doit au moins correspondre à l'énergie électrostatique de répulsion\(E = (4\pi\epsilon_0)^{-1}Ze^2/R_0\) (où +Ze est la charge du noyau). De cette façon, nous pouvons estimer la largeur de la barrière nucléaire,
\[L = \frac{e^2}{4\pi\epsilon_0} \frac{Z}{E} - R. \nonumber \]
Cette estimation montre que plus l'énergie d'une particule α est élevée, plus la largeur de la barrière qu'elle doit traverser est étroite. Nous savons également que la largeur de la barrière potentielle est le paramètre le plus important de la probabilité de creusement d'un tunnel. Ainsi, les particules α à haute énergie ont de bonnes chances de s'échapper du noyau et, pour de tels noyaux, la demi-vie de désintégration nucléaire est courte. Notez que ce processus est hautement non linéaire, ce qui signifie qu'une légère augmentation de l'énergie des particules α a un effet d'augmentation disproportionné sur la probabilité de création d'un tunnel et, par conséquent, sur le raccourcissement de la demi-vie. Cela explique pourquoi la demi-vie du polonium qui émet des particules α de 8 MeV n'est que de centaines de millisecondes et la demi-vie de l'uranium qui émet des particules α de 4 MeV est de milliards d'années.
Émission de terrain
L'émission de champ est un processus d'émission d'électrons à partir de surfaces conductrices en raison d'un fort champ électrique externe appliqué dans la direction normale à la surface (Figure\(\PageIndex{4}\)). Comme nous le savons grâce à notre étude des champs électriques dans les chapitres précédents, un champ électrique externe appliqué amène les électrons d'un conducteur à se déplacer vers sa surface et à y rester tant que le champ externe actuel n'est pas excessivement fort. Dans cette situation, nous avons un potentiel électrique constant à l'intérieur du conducteur, y compris à sa surface. Dans le langage de l'énergie potentielle, nous disons qu'un électron à l'intérieur du conducteur a une énergie potentielle constante\(U(x) - -U_0\) (ici, le x signifie à l'intérieur du conducteur).
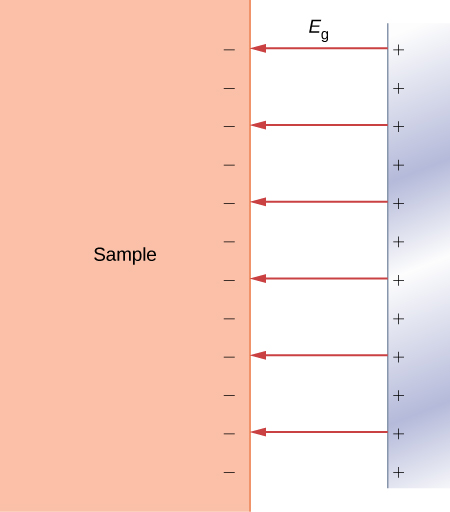
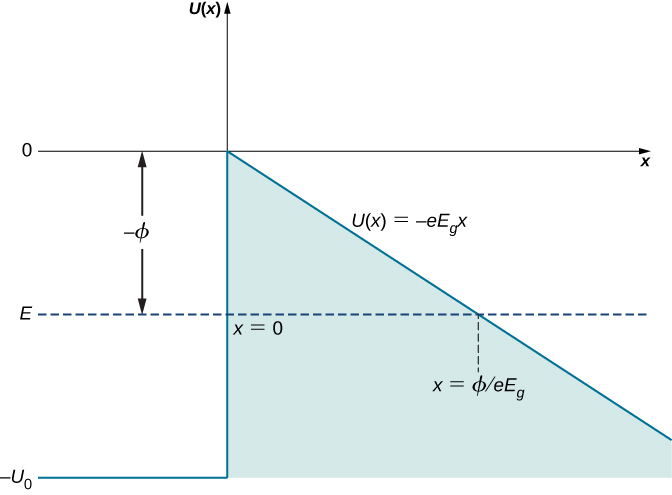
Dans la situation représentée sur la figure\(\PageIndex{4}\), où le champ électrique externe est uniforme et a une amplitude\(E_g\), si un électron se trouve à l'extérieur du conducteur à une distance x de sa surface, son énergie potentielle devrait être\(U(x) = -eE_gx\) (ici, x désigne distance par rapport à la surface). En prenant l'origine à la surface,\(x = 0\) c'est-à-dire l'emplacement de la surface, nous pouvons représenter l'énergie potentielle des électrons de conduction dans un métal sous la forme de la barrière d'énergie potentielle illustrée sur la figure\(\PageIndex{5}\). En l'absence de champ externe, l'énergie potentielle devient une barrière progressive définie par\(U(x \leq 0) = -U_0\) et par\(U(x > 0) = 0\).
Lorsqu'un champ électrique externe est fort, les électrons de conduction présents à la surface peuvent s'en détacher et accélérer le long des lignes de champ électrique dans une direction antiparallèle au champ externe, loin de la surface. En bref, les électrons de conduction peuvent s'échapper de la surface. L'émission de champ peut être comprise comme le tunnel quantique des électrons de conduction à travers la barrière de potentiel à la surface du conducteur. Le principe physique à l'œuvre ici est très similaire au mécanisme de l'émission α à partir d'un noyau radioactif.
Supposons qu'un électron de conduction possède une énergie cinétique E (l'énergie cinétique moyenne d'un électron dans un métal est la fonction de travail φ pour le métal et peut être mesurée, comme indiqué pour l'effet photoélectrique dans les photons et les ondes de matière), et qu'un champ électrique externe peut être local approchée par un champ électrique uniforme de force\(E_g\). La largeur L de la barrière de potentiel que l'électron doit traverser est la distance entre la surface du conducteur et le point extérieur à la surface où son énergie cinétique correspond à la valeur de son énergie potentielle dans le champ extérieur. Sur la figure\(\PageIndex{5}\), cette distance est mesurée le long de la ligne horizontale en pointillés\(U(x) = E\) depuis\(x = 0\) l'intersection avec\(U(x) = -eE_gx\), de sorte que la largeur de la barrière est
\[L = \frac{e^{-1}E}{E_g} = \frac{e^{-1}\phi}{E_g} \nonumber \]
Nous voyons que L est inversement proportionnel à l'intensité\(E_g\) d'un champ extérieur. Lorsque nous augmentons l'intensité du champ externe, la barrière de potentiel à l'extérieur du conducteur devient plus raide et sa largeur diminue pour un électron ayant une énergie cinétique donnée. À son tour, la probabilité qu'un électron traverse la barrière (surface du conducteur) devient exponentiellement plus grande. Les électrons qui émergent de l'autre côté de cette barrière forment un courant (courant d'électrons à effet tunnel) qui peut être détecté au-dessus de la surface. Le courant d'électrons à effet tunnel est proportionnel à la probabilité de tunnellisation. La probabilité de creusement d'un tunnel dépend de manière non linéaire de la largeur de la barrière L, et L peut être modifiée en ajustant\(E_g\). Par conséquent, le courant d'électrons à effet tunnel peut être réglé en ajustant l'intensité d'un champ électrique externe à la surface. Lorsque l'intensité d'un champ électrique externe est constante, le courant d'électrons à effet tunnel a des valeurs différentes à différentes altitudes L au-dessus de la surface.
Le phénomène de tunneling quantique sur des surfaces métalliques, que nous venons de décrire, est le principe physique qui sous-tend le fonctionnement du microscope à effet tunnel à balayage (STM), inventé en 1981 par Gerd Binnig et Heinrich Rohrer. Le dispositif STM comprend une pointe de numérisation (une aiguille, généralement en tungstène, platine-iridium ou or) ; un dispositif piézoélectrique qui contrôle l'élévation de la pointe dans une plage typique de 0,4 à 0,7 nm au-dessus de la surface à scanner ; un dispositif qui contrôle le mouvement de la pointe le long de la surface ; et un ordinateur pour afficher des images. Lorsque l'échantillon est maintenu à une polarisation de tension appropriée, la pointe de balayage se déplace le long de la surface (Figure\(\PageIndex{6}\)) et le courant d'électrons à effet tunnel entre la pointe et la surface est enregistré à chaque position.
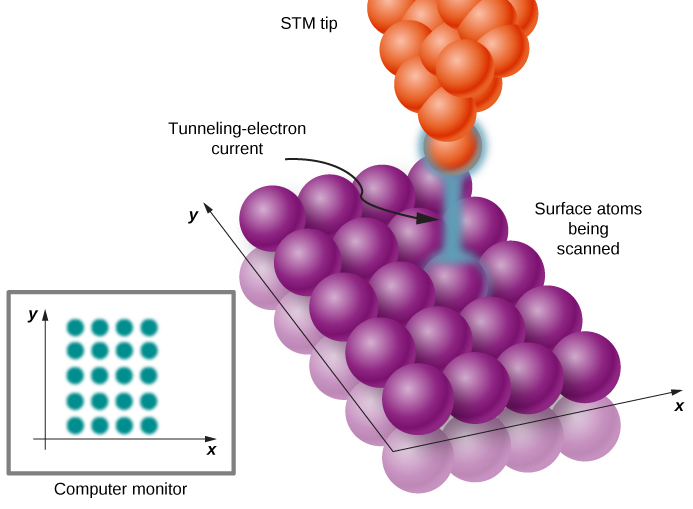
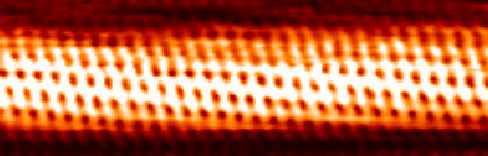
La quantité de courant dépend de la probabilité d'un effet tunnel d'électrons de la surface à la pointe, qui, à son tour, dépend de l'élévation de la pointe au-dessus de la surface. Ainsi, à chaque position de pointe, la distance entre la pointe et la surface est mesurée en mesurant le nombre d'électrons qui traversent la surface par tunnel jusqu'à la pointe. Cette méthode permet d'obtenir une résolution sans précédent d'environ 0,001 nm, soit environ 1 % du diamètre moyen d'un atome. De cette façon, nous pouvons voir des atomes individuels à la surface, comme sur l'image d'un nanotube de carbone sur la figure\(\PageIndex{7}\).
Tunneling quantique résonnant
Le tunneling quantique a de nombreuses applications dans les dispositifs à semi-conducteurs tels que les composants de circuits électroniques ou les circuits intégrés conçus à l'échelle nanométrique ; d'où le terme « nanotechnologie ». Par exemple, une diode (un élément de circuit électrique qui fait en sorte qu'un courant d'électrons dans un sens soit différent du courant dans le sens opposé, lorsque la polarité de la tension de polarisation est inversée) peut être réalisée par une jonction à effet tunnel entre deux types différents de matériaux semi-conducteurs. Dans une telle diode tunnel, les électrons traversent une barrière de potentiel unique au niveau d'un contact entre deux semi-conducteurs différents. Au niveau de la jonction, le courant des électrons à effet tunnel change de façon non linéaire en fonction de la différence de potentiel appliquée à travers la jonction et peut diminuer rapidement à mesure que la tension de polarisation augmente. Cela ne ressemble pas au comportement de la loi d'Ohm que nous connaissons bien dans les circuits domestiques. Ce type de comportement rapide (provoqué par le tunneling quantique) est souhaitable dans les appareils électroniques à haut débit.
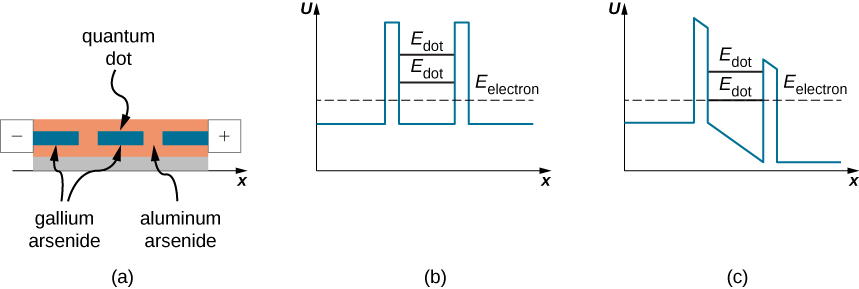
Un autre type de nano-dispositif électronique utilise la tunnellisation résonnante d'électrons à travers des barrières potentielles qui se trouvent dans les points quantiques. Un point quantique est une petite région d'un nanocristal semi-conducteur que l'on fait croître, par exemple, dans un cristal d'arséniure de silicium ou d'aluminium. La figure\(\PageIndex{8a}\) montre un point quantique d'arséniure de gallium intégré dans une plaquette d'arséniure d'aluminium. La région des points quantiques agit comme un puits potentiel d'une hauteur finie (Figure\(\PageIndex{8b}\)) doté de deux barrières de potentiel de hauteur finie aux limites des points. De même, comme pour une particule quantique dans une boîte (c'est-à-dire un puits de potentiel infini), les énergies inférieures d'une particule quantique piégée dans un puits de potentiel de hauteur finie sont quantifiées. La différence entre le potentiel de la boîte et celui du puits est qu'une particule quantique dans une boîte possède un nombre infini d'énergies quantifiées et est piégée dans la boîte indéfiniment, alors qu'une particule quantique piégée dans un puits potentiel possède un nombre fini de niveaux d'énergie quantifiés et peut traverser le potentiel des barrières situées aux limites du puits vers l'extérieur du puits. Ainsi, un point quantique d'arséniure de gallium situé dans de l'arséniure d'aluminium est un puits potentiel où les basses énergies d'un électron sont quantifiées, comme indiqué\(E_{dot}\) dans la partie (b) de la figure. Lorsque l'énergie\(E_{electron}\) d'un électron dans la région extérieure du point ne correspond pas à l'énergie\(E_{dot}\) qu'il aurait dans le point, l'électron ne traverse pas la région du point et aucun courant ne traverse un tel élément de circuit, même s'il était maintenu à une différence de tension électrique (biais). Cependant, lorsque cette polarisation de tension est modifiée de telle sorte que l'une des barrières est abaissée, de sorte qu'elle\(E_{dot}\)\(E_{electron}\) s'aligne, comme le montre la partie (c) de la figure, un courant d'électrons circule à travers le point. Lorsque la polarisation de tension est maintenant augmentée, cet alignement est perdu et le courant cesse de circuler. Lorsque la polarisation de tension augmente davantage, la tunnellisation électronique devient improbable jusqu'à ce que la tension de polarisation atteigne une valeur pour laquelle l'énergie électronique extérieure correspond au niveau d'énergie électronique suivant dans le point. Le mot « résonance » dans le nom de l'appareil signifie que le courant d'électrons à effet tunnel se produit uniquement lorsqu'un niveau d'énergie sélectionné est adapté en réglant une polarisation de tension appliquée, comme dans le mécanisme de fonctionnement de la diode à effet tunnel résonant qui vient d'être décrite. Les diodes à effet tunnel résonnant sont utilisées comme nano-commutateurs ultrarapides.