7.6 : L'oscillateur harmonique quantique
- Page ID
- 189845
À la fin de cette section, vous serez en mesure de :
- Décrire le modèle de l'oscillateur harmonique quantique
- Identifier les différences entre les modèles classique et quantique de l'oscillateur harmonique
- Expliquer les situations physiques où les modèles classique et quantique coïncident
Les oscillations se retrouvent partout dans la nature, notamment sous forme d'ondes électromagnétiques, de molécules vibrantes et du léger mouvement de va-et-vient d'une branche d'arbre. Dans les chapitres précédents, nous avons utilisé la mécanique newtonienne pour étudier les oscillations macroscopiques, telles qu'un bloc sur un ressort et un simple pendule. Dans ce chapitre, nous commençons à étudier les systèmes oscillants en utilisant la mécanique quantique. Nous commençons par une revue de l'oscillateur harmonique classique.
L'oscillateur harmonique classique
Un oscillateur harmonique simple est une particule ou un système qui subit un mouvement harmonique autour d'une position d'équilibre, tel qu'un objet dont la masse vibre sur un ressort. Dans cette section, nous examinons les oscillations unidimensionnelles uniquement. Supposons qu'une masse se déplace d'avant en arrière dans la\(x\) direction -autour de la position d'équilibre,\(x = 0\). En mécanique classique, la particule se déplace en réponse à une force de rappel linéaire donnée par\(F_x = -kx\), où\(x\) est le déplacement de la particule par rapport à sa position d'équilibre. Le mouvement a lieu entre deux points de retournement\(x \pm A\), où A indique l'amplitude du mouvement. La position de l'objet varie périodiquement dans le temps avec la fréquence angulaire\(\omega = \sqrt{k/m}\), qui dépend de la masse m de l'oscillateur et de la constante\(k\) de force de la force nette, et peut être écrite comme
\[x(t) = A \, \cos (\omega t + \phi). \label{7.52} \]
L'énergie totale\(E\) d'un oscillateur est la somme de son énergie cinétique\(K = mu^2/2\) et de l'énergie potentielle élastique de la force\(U(x) = kx^2/2\),
\[E = \dfrac{1}{2} mu^2 + \dfrac{1}{2}kx^2. \label{7.53} \]
Aux points de retournement\(x = \pm A\), la vitesse de l'oscillateur est nulle ; par conséquent, à ces points, l'énergie d'oscillation est uniquement sous forme d'énergie potentielle\(E = kA^2/2\). Le diagramme de l'énergie potentielle\(U(x)\) de l'oscillateur en fonction de sa position\(x\) est une parabole (Figure\(\PageIndex{1}\)). La fonction d'énergie potentielle est une fonction quadratique de\(x\), mesurée par rapport à la position d'équilibre. Sur le même graphique, nous tracons également l'énergie totale\(E\) de l'oscillateur, sous la forme d'une ligne horizontale qui intercepte la parabole à\(x = \pm A\). Ensuite, l'énergie cinétique\(K\) est représentée comme la distance verticale entre la ligne d'énergie totale et la parabole d'énergie potentielle.
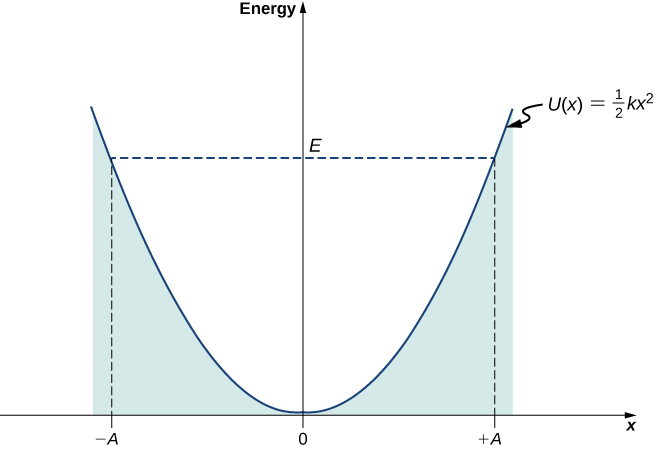
Dans ce diagramme, le mouvement d'un oscillateur classique est limité à la région où son énergie cinétique n'est pas négative, comme le dit l'équation de relation énergétique \ ref {7.53}. Physiquement, cela signifie qu'un oscillateur classique ne peut jamais être trouvé au-delà de ses points de rotation et que son énergie dépend uniquement de la distance entre les points de rotation et sa position d'équilibre. L'énergie d'un oscillateur classique change de façon continue. L'énergie la plus faible qu'un oscillateur classique peut avoir est nulle, ce qui correspond à une situation où un objet est au repos à sa position d'équilibre. L'état d'énergie nulle d'un oscillateur classique signifie simplement qu'il n'y a aucune oscillation ni aucun mouvement (une particule classique se trouve au bas du puits de potentiel sur la figure\(\PageIndex{1}\)). Lorsqu'un objet oscille, quelle que soit la taille de son énergie, il passe le plus de temps à proximité des points de retournement, car c'est là qu'il ralentit et inverse sa direction de mouvement. Par conséquent, la probabilité de trouver un oscillateur classique entre les points de retournement est la plus élevée à proximité des points de retournement et la plus faible à la position d'équilibre. (Notez qu'il ne s'agit pas d'une déclaration de préférence de l'objet à utiliser pour réduire son énergie. Il s'agit d'une déclaration sur la rapidité avec laquelle l'objet se déplace dans différentes régions.)
L'oscillateur harmonique quantique
L'un des problèmes de cette formulation classique est qu'elle n'est pas générale. Nous ne pouvons pas l'utiliser, par exemple, pour décrire les vibrations de molécules diatomiques, où les effets quantiques sont importants. Une première étape vers une formulation quantique consiste à utiliser l'expression classique\(k = m\omega^2\) pour limiter la mention d'une constante « ressort » entre les atomes. De cette façon, la fonction d'énergie potentielle peut être écrite sous une forme plus générale,
\[U(x) = \dfrac{1}{2}m \omega^2 x^2. \label{7.54} \]
La combinaison de cette expression avec l'équation de SchrDinger indépendante du temps donne
\[-\dfrac{\hbar}{2m} \dfrac{d^2 \psi(x)}{dx^2} + \dfrac{1}{2}m\omega^2 x^2 \psi(x) = E\psi (x). \label{7.55} \]
Pour résoudre l'équation \ ref {7.55}, c'est-à-dire pour trouver les énergies autorisées\(E\) et leurs fonctions d'onde\(\psi (x) \) correspondantes, nous avons besoin que les fonctions d'onde soient symétriques par rapport à\(x = 0\) (le bas du puits de potentiel) et qu'elles soient normalisables. Ces conditions garantissent que la densité de probabilité\(|\psi (x)|^2\) doit être finie lorsqu'elle est intégrée sur toute la plage de x comprise entre\(-\infty\) et\(+\infty\). Comment résoudre l'équation \ ref {7.55} fait l'objet d'un cours plus avancé en mécanique quantique ; ici, nous citons simplement les résultats. Les énergies autorisées sont
\[ \begin{align} E_n &= \left(n + \dfrac{1}{2}\right) \hbar \omega \\[5pt] &= \dfrac{2n + 1}{2} \hbar \omega \label{7.56} \end{align} \]
avec\(n = 0,1,2,3,...\)
Les fonctions d'onde qui correspondent à ces énergies (états stationnaires ou états d'énergie définie) sont
\[\psi_n (x) = N_n e^{-\beta^2 x^2/2} H_n (\beta x), \, n = 0,1,2,3, ... \label{7.57} \]
où\(\beta = \sqrt{m\omega/\hbar}\),\(N_n\) est la constante de normalisation et\(H_n(y)\) est un polynôme de degré\(n\) appelé polynôme d'Hermite. Les quatre premiers polynômes d'Hermite sont
- \(H_0 (y) = 1\)
- \(H_1 (y) = 2y\)
- \(H_2 (y) = 4y^2 - 2\)
- \(H_3 (y) = 8y^3 - 12 y.\)
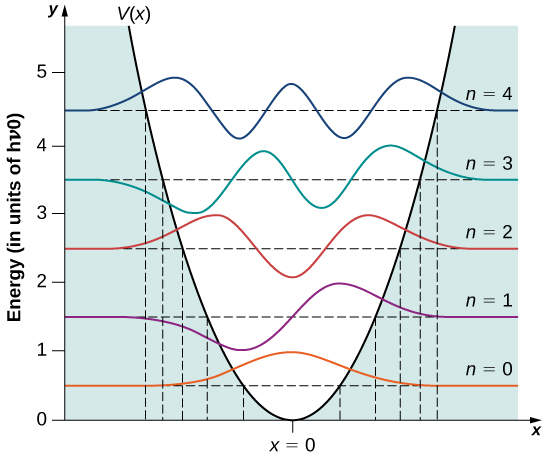
Quelques exemples de fonctions d'onde sont présentés dans la figure\(\PageIndex{2}\). À mesure que la valeur du nombre principal augmente, les solutions alternent entre des fonctions paires et des fonctions impaires environ\(x = 0\).
Détermine l'amplitude\(A\) des oscillations d'un oscillateur classique dont l'énergie est égale à l'énergie d'un oscillateur quantique à l'état quantique\(n\).
Stratégie
Pour déterminer l'amplitude\(A\), nous avons défini l'énergie classique\(E = kx^2/2 = m\omega^2 \, A^2/2\) égale à celle\(E_n\) donnée par l'équation \ ref {7.56}.
Solution
Nous obtenons
\[\begin{align} E_n &= m\omega^2 A_n^2/2 \nonumber \\[5pt] A_n &= \sqrt{\dfrac{2}{m\omega^2}E_n} \nonumber \\[5pt] &= \sqrt{\dfrac{2}{m\omega^2} \dfrac{2n + 1}{2}\hbar \omega} \nonumber \\[5pt] &= \sqrt{(2n + 1) \dfrac{\hbar}{m\omega}}. \nonumber \end{align} \nonumber \]
L'importance
Lorsque le nombre quantique n augmente, l'énergie de l'oscillateur et donc l'amplitude de l'oscillation augmentent (pour une fréquence angulaire naturelle fixe). Pour un grand n, l'amplitude est approximativement proportionnelle à la racine carrée du nombre quantique.
Plusieurs fonctionnalités intéressantes apparaissent dans cette solution. Contrairement à un oscillateur classique, les énergies mesurées d'un oscillateur quantique ne peuvent avoir que des valeurs énergétiques données par l'équation \ ref {7.56}. De plus, contrairement à ce qui se passe pour une particule quantique dans une boîte, les niveaux d'énergie admissibles sont régulièrement espacés,
\[\begin{align} \Delta E &= E_{n+1} - E_n \\[5pt] &= \dfrac{2(n + 1) + 1}{2} \hbar \omega - \dfrac{2n + 1}{2} \hbar \omega \\[5pt] &= \hbar \omega = hf. \label{7.58} \end{align} \]
Lorsqu'une particule liée à un tel système passe d'un état d'énergie supérieure à un état d'énergie inférieure, le plus petit quantum d'énergie transporté par le photon émis est nécessairement\(hf\). De même, lorsque la particule passe d'un état de faible énergie à un état d'énergie plus élevée, le plus petit quantum d'énergie pouvant être absorbé par la particule est\(hf\). Un oscillateur quantique ne peut absorber ou émettre de l'énergie que par multiples de ce plus petit quantum d'énergie. Ceci est conforme à l'hypothèse de Planck concernant les échanges d'énergie entre le rayonnement et les parois de la cavité dans le cadre du problème du rayonnement du corps noir.
La molécule\(\ce{HCl}\) diatomique est constituée d'un atome de chlore et d'un atome d'hydrogène. Comme l'atome de chlore est 35 fois plus massif que l'atome d'hydrogène, les vibrations de la\(\ce{HCl}\) molécule peuvent être assez bien approximées en supposant que l'atome de Cl est immobile et que l'atome H effectue des oscillations harmoniques en raison d'une force moléculaire élastique modélisée par la loi de Hooke. Le spectre vibrationnel infrarouge mesuré pour le chlorure d'hydrogène a la raie de fréquence la plus basse centrée sur\(f = 8.88 \times 10^{13} Hz\). Quel est l'espacement entre les énergies vibratoires de cette molécule ? Quelle est la constante de force k de la liaison atomique dans la molécule de HCl ?
Stratégie
La raie de fréquence la plus basse correspond à l'émission de photons de fréquence la plus basse. Ces photons sont émis lorsque la molécule effectue une transition entre deux niveaux d'énergie vibratoire adjacents. En supposant que les niveaux d'énergie sont également espacés, nous utilisons l'équation \ ref {7.58} pour estimer l'espacement. La molécule est bien approximée en traitant l'atome de Cl comme étant infiniment lourd et l'atome H comme la masse\(m\) qui effectue les oscillations. En traitant ce système moléculaire comme un oscillateur classique, la constante de force est déterminée à partir de la relation classique\(k = m\omega^2\).
Solution
L'espacement énergétique est
\[ \begin{align} \Delta E &= hf \nonumber \\[5pt] &= (4.14 \times 10^{-15} eV \cdot s)(8.88 \times 10^{13} Hz) \nonumber\\[5pt] &= 0.368 \, eV. \nonumber \end{align} \nonumber \]
La constante de force est
\[ \begin{align} k &= m \omega^2 \nonumber \\[5pt] &= m (2\pi f)^2 \nonumber \\[5pt] &= (1.67 \times 10^{ −27} kg)(2\pi \times 8.88 \times 10 ^{13}Hz)^2 \nonumber \\[5pt] &= 520 \, N/m. \nonumber \end{align} \nonumber \]
L'importance
La force entre les atomes d'une molécule de HCl est étonnamment forte. L'énergie typique libérée lors des transitions énergétiques entre les niveaux vibratoires se situe dans la gamme infrarouge. Comme nous le verrons plus loin, les transitions entre les niveaux d'énergie vibratoire d'une molécule diatomique accompagnent souvent les transitions entre les niveaux d'énergie de rotation.
La fréquence vibratoire de la molécule diatomique d'iodure d'hydrogène HI est\(6.69×10^{ 13}\,Hz\).
- Quelle est la constante de force de la liaison moléculaire entre les atomes d'hydrogène et d'iode ?
- Quelle est l'énergie du photon émis lorsque cette molécule effectue une transition entre des niveaux d'énergie vibratoire adjacents ?
- Répondez à une
-
295 N/m
- Réponse b
-
0,277 eV
L'oscillateur quantique diffère de l'oscillateur classique de trois manières :
- Premièrement, l'état fondamental d'un oscillateur quantique n'est\(E_0 = \hbar \omega /2\) pas nul. Dans la vision classique, l'énergie la plus faible est nulle. L'absence d'un état à énergie nulle est commune à tous les systèmes de mécanique quantique en raison de fluctuations omniprésentes qui sont une conséquence du principe d'incertitude de Heisenberg. Si une particule quantique restait immobile au fond du puits potentiel, sa quantité de mouvement et sa position devraient être exactes à la fois, ce qui violerait le principe d'incertitude de Heisenberg. Par conséquent, l'état d'énergie la plus faible doit être caractérisé par des incertitudes quant à la quantité de mouvement et à la position, de sorte que l'état fondamental d'une particule quantique doit se situer au-dessus du fond du puits potentiel.
- Ensuite, une particule dans un potentiel d'oscillateur harmonique quantique peut être trouvée avec une probabilité non nulle en dehors de l'intervalle\(-A \leq x \leq +A\). Dans une formulation classique du problème, la particule n'aurait aucune énergie pour se trouver dans cette région. La probabilité de trouver une particule quantique à l'état fondamental dans la région classiquement interdite est d'environ 16 %.
- Troisièmement, les distributions de densité de probabilité\(|\psi_n(x)|^2\) pour un oscillateur quantique à l'état de faible énergie du sol sont les plus importantes au milieu du puits\((x = 0)\).\(\psi_0(x)\) Pour que la particule soit trouvée avec la plus grande probabilité au centre du puits, nous nous attendons à ce que la particule y passe le plus de temps lorsqu'elle oscille. Cela est contraire au comportement d'un oscillateur classique, dans lequel la particule passe le plus clair de son temps à se déplacer à des vitesses relativement faibles à proximité des points de retournement.
Déterminez la valeur attendue de la position d'une particule dans l'état fondamental d'un oscillateur harmonique en utilisant la symétrie.
- Réponse b
-
\[\langle x \rangle = 0 \nonumber \]
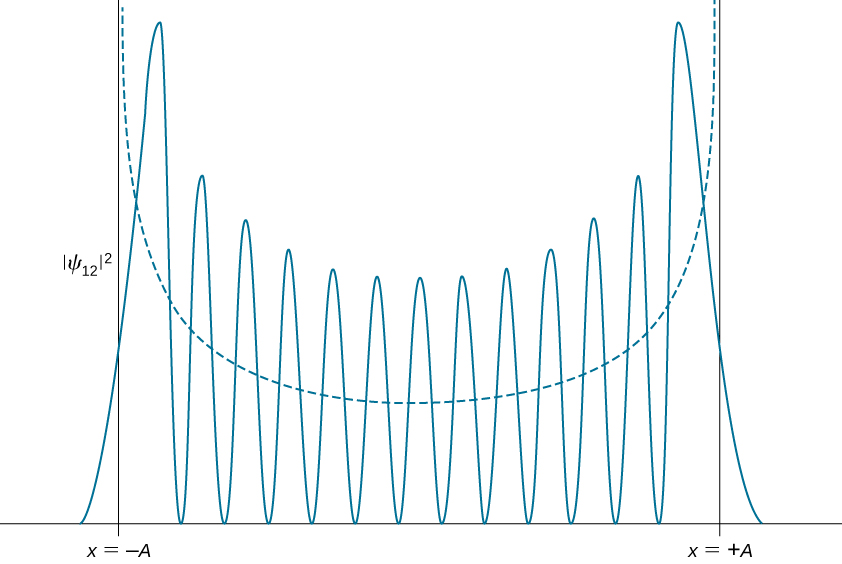
Les distributions de densité de probabilité quantique changent de caractère pour les états excités, ressemblant davantage à la distribution classique lorsque le nombre quantique augmente. Nous observons déjà ce changement pour le premier état excité d'un oscillateur quantique, car la distribution\(|\psi_1(x)|^ 2\) atteint un pic autour des points de rotation et disparaît à la position d'équilibre, comme le montre la Figure\(\PageIndex{2}\). Conformément au principe de correspondance de Bohr, dans la limite des nombres quantiques élevés, la description quantique d'un oscillateur harmonique converge vers la description classique, illustrée sur la figure\(\PageIndex{3}\). La distribution de densité de probabilité classique correspondant à l'énergie quantique de l'\(n = 12\)état est une approximation raisonnablement bonne de la distribution de probabilité quantique pour un oscillateur quantique dans cet état excité. Cet accord s'améliore de plus en plus pour les États très enthousiastes.