7.5 : La particule quantique dans une boîte
- Page ID
- 189888
À la fin de cette section, vous serez en mesure de :
- Décrire comment configurer un problème de valeurs limites pour l'équation stationnaire de SchrDinger
- Expliquer pourquoi l'énergie d'une particule quantique dans une boîte est quantifiée
- Décrire la signification physique des solutions stationnaires à l'équation de Schrdinger et la connexion de ces solutions avec des états quantiques dépendants du temps
- Expliquer la signification physique du principe de correspondance de Bohr
Dans cette section, nous appliquons l'équation de Schrdinger à une particule liée à une boîte unidimensionnelle. Ce cas particulier fournit des leçons pour comprendre la mécanique quantique dans des systèmes plus complexes. L'énergie de la particule est quantifiée en conséquence d'une condition d'onde stationnaire à l'intérieur de la boîte.
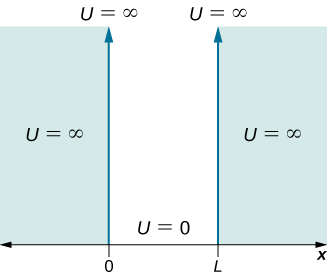
Supposons\(m\) qu'une particule de masse ne soit autorisée à se déplacer que le long de la direction x et dont le mouvement est limité à la région située entre les parois dures et rigides situées à\(x = 0\) et à\(x = L\) (Figure\(\PageIndex{1}\)). Entre les parois, la particule se déplace librement. Cette situation physique est appelée puits carré infini, décrite par la fonction d'énergie potentielle
\ [U (x) = \ begin {cas}
0 et 0 \ leq x \ leq L \ \
\ infty & x< 0 \ ; and \ ; x> L \ end {cas} \ label {3.5.2} \]
La combinaison de cette équation avec l'équation d'onde indépendante du temps de SchrDinger donne
\[\dfrac{-\hbar^2}{2m} \dfrac{d^2\psi(x)}{dx^2} = E\psi(x), \, for \, 0 \leq x \leq L \label{7.32} \]
où\(E\) est l'énergie totale de la particule. Quels types de solutions attendons-nous ? L'énergie de la particule est un nombre positif, donc si la valeur de la fonction d'onde est positive (côté droit de l'équation), la courbure de la fonction d'onde est négative ou concave vers le bas (côté gauche de l'équation). De même, si la valeur de la fonction d'onde est négative (côté droit de l'équation), la courbure de la fonction d'onde est positive ou concave vers le haut (côté gauche de l'équation). Cette condition est remplie par une fonction d'onde oscillante, telle qu'une onde sinusoïdale ou cosinusoïdale. Comme ces ondes sont confinées dans la boîte, nous envisageons des ondes stationnaires avec des points d'extrémité fixes à\(x = 0\) et\(x = L\).
Les solutions\(\psi(x)\) à cette équation reposent sur une interprétation probabiliste. En particulier, le carré\(|\psi(x)|^2\) représente la densité de probabilité de trouver la particule à un endroit donné x. Cette fonction doit être intégrée pour déterminer la probabilité de trouver la particule dans un certain intervalle de l'espace. Nous recherchons donc une solution normalisable qui satisfasse à la condition de normalisation suivante :
\[\int_0^L dx|\psi(x)|^2 = 1. \label{7.33} \]
Les parois sont rigides et impénétrables, ce qui signifie que la particule ne se trouve jamais au-delà de la paroi. Mathématiquement, cela signifie que la solution doit disparaître au niveau des parois :
\[\psi(0) = \psi(L) = 0. \label{7.34} \]
Nous nous attendons à des solutions oscillantes, donc la solution la plus générale à cette équation est
\[\psi_k(x) = A_k \, \cos \, kx + B_k \, \sin \, kx \label{7.35} \]
où\(k\) est le nombre d'ondes, et\(A_k\) et\(B_k\) sont des constantes. L'application de la condition limite exprimée par l'équation \ ref {7.33} donne
\[\psi_k(0) = A_k \, \cos (k \cdot 0) + B_k \, \sin (k \cdot 0) = A_k = 0. \label{7.36} \]
Parce que c'est le\(A_k = 0\) cas, la solution doit être
\[\psi_k(x) = B_k \, \sin \, kx. \label{7.37} \]
Si\(B_k\) vaut zéro, alors\(\psi_k(x) = 0\) pour toutes les valeurs de\(x\) et la condition de normalisation (Équation \ ref {7.33}) ne peuvent pas être satisfaites. En supposant que\(B_k \neq 0\) l'équation \ ref {7.34} pour\(x = L\) then donne
\[0 = B_k \, \sin (kL) \Rightarrow \sin(kL) = 0 \Rightarrow kL = n\pi, \, n = 1,2,3,... \label{7.38} \]
Nous rejetons la\(n = 0\) solution parce que\(\psi(x)\) pour ce nombre quantique, il y aurait zéro partout, une solution non normalisable et donc non physique. La substitution de l'équation \ ref {7.37} par l'équation \ ref {7.32} donne
\[-\dfrac{\hbar^2}{2m}\dfrac{d^2}{dx^2} (B_k \sin(kx)) = E(B_k \sin(kx)). \label{7.39} \]
Le calcul de ces dérivés conduit à
\[E = E_k = \dfrac{\hbar^2k^2}{2m}. \label{7.40} \]
Selon de Broglie\(p = \hbar k\), cette expression implique donc que l'énergie totale est égale à l'énergie cinétique, conformément à notre hypothèse selon laquelle « la particule se déplace librement ». La combinaison des résultats des équations \ ref {7.38} et \ ref {7.40} donne
\[E_n = n^2 \dfrac{\pi^2 \hbar^2}{2mL^2}, \, n = 1,2,3,... \label{7.41} \]
L'équation \ ref {7.41} soutient qu'une particule liée à une boîte unidimensionnelle ne peut avoir que certaines valeurs d'énergie discrètes (quantifiées). De plus, la particule ne peut pas avoir une énergie cinétique nulle ; il est impossible qu'une particule liée à une boîte soit « au repos ».
Pour évaluer les fonctions d'onde autorisées qui correspondent à ces énergies, nous devons trouver la constante de normalisation\(B_n\). Nous imposons la condition de normalisation Equation \ ref {7.33} à la fonction d'onde
\[\psi_n(x) = B_n \, \sin \, \dfrac{n\pi x}{L} \label{7.42} \]
Nous commençons par la condition de normalisation (Équation \ ref {7.33})
\[\begin{align} 1 &= \int_0^L dx|\psi_n(x)|^2 \\[5pt] &= \int_0^L dx \, B_n^2 \, \sin^2 \dfrac{n\pi}{L} x \\[5pt] &= B^2 n \int_0^2 dx \, \sin^2 \dfrac{n\pi}{L}x \\[5pt] &= B_n^2 \dfrac{L}{2} \\[5pt] \Rightarrow B_n &= \sqrt{\dfrac{2}{L}}. \end{align} \nonumber \]
Par conséquent, les fonctions d'onde qui correspondent aux valeurs d'énergie données dans l'équation \ ref {7.41} sont
\[\psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.43} \]
Pour l'état énergétique le plus bas ou l'énergie de l'état fondamental, nous avons
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2}, \, \psi_1(x) = \sqrt{\dfrac{2}{L}} \, \sin \left(\dfrac{\pi x}{L}\right). \label{7.44} \]
Tous les autres états énergétiques peuvent être exprimés sous la forme
\[E_n = n^2 E_1, \, \psi_n(x) = \sqrt{\dfrac{2}{L}} \, \sin \, \left(\dfrac{n\pi x}{L}\right). \label{7.45} \]
L'indice\(n\) est appelé nombre quantique d'énergie ou nombre quantique principal. L'état pour\(n = 2\) est le premier état excité, l'état pour\(n = 3\) est le second état excité, et ainsi de suite. Les trois premiers états quantiques (pour n = 1, 2 et 3) d'une particule dans une boîte sont illustrés sur la figure\(\PageIndex{2}\). Les fonctions d'onde de l'équation \ ref {7.45} sont parfois appelées « états d'énergie définie ». On dit que les particules dans ces états occupent des niveaux d'énergie, qui sont représentés par les lignes horizontales de la figure\(\PageIndex{2}\). Les niveaux d'énergie sont analogues aux échelons d'une échelle que la particule peut « gravir » lorsqu'elle gagne ou perd de l'énergie.
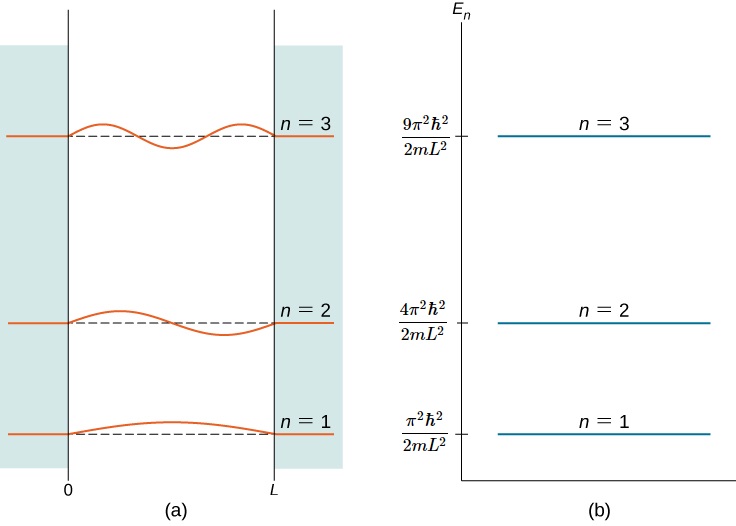
Les fonctions d'onde de l'équation \ ref {7.45} sont également appelées états stationnaires et états d'ondes stationnaires. Ces fonctions sont « stationnaires », parce que leurs fonctions de densité de probabilité ne varient pas dans le temps, et « ondes stationnaires », parce que leurs parties réelles et imaginaires oscillent de haut en bas comme une onde stationnaire, comme une corde qui agite entre deux enfants sur un terrain de jeu.\(|\Psi(x,t)|^2\) Les états stationnaires sont des états d'énergie définie (équation \ ref {7.45}), mais des combinaisons linéaires de ces états, telles que\(\psi(x) = a\psi_1 + b\psi_2\) (également des solutions à l'équation de Schrdinger) sont des états d'énergie mixte.
La quantification de l'énergie est une conséquence des conditions limites. Si la particule n'est pas confinée dans une boîte mais qu'elle se déplace librement, les énergies autorisées sont continues. Cependant, dans ce cas, seules certaines énergies (\(E_1, 4E_1, 9E_1,...\)) sont autorisées. La différence d'énergie entre les niveaux d'énergie adjacents est donnée par
\[\Delta E_{n+1,n} = E_{n+1} - E_n = (n + 1)^2 E_1 - n^2E_1 = (2n + 1) E_1. \nonumber \]
La conservation de l'énergie exige que, si l'énergie du système change, la différence d'énergie soit répercutée sur une autre forme d'énergie. Dans le cas particulier d'une particule chargée confinée dans un petit volume (par exemple, dans un atome), les changements d'énergie sont souvent entraînés par des photons. Les fréquences des photons émis nous fournissent des informations sur les différences d'énergie (espacements) du système et le volume de confinement, c'est-à-dire la taille de la « boîte » (Équation \ ref {7.44}).
Supposons qu'un proton soit confiné dans une boîte de largeur\(L = 1.00 \times 10^{-14} m\) (un rayon nucléaire typique). Quelles sont les énergies du sol et les premiers états excités ? Si le proton passe du premier état excité à l'état fondamental, quelles sont l'énergie et la fréquence du photon émis ?
Stratégie
Si nous supposons que le proton confiné dans le noyau peut être modélisé comme une particule quantique dans une boîte, il suffit d'utiliser l'équation \ ref {7.41} pour trouver ses énergies\(E_1\) et\(E_2\). La masse d'un proton est\(m = 1.76 \times 10^{-27}kg\). Le photon émis emporte la différence d'énergie\(\Delta E = E_2 - E_1\). Nous pouvons utiliser la relation\(E_f = hf\) pour trouver sa fréquence f.
Solution
État fondamental :
\[\begin{align*} E_1 &= \dfrac{\pi^2 \hbar^2}{2mL^2} \\[5pt] &= \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)}{2(1.67 \times 10^{-27} kg)(1.00 \times 10^{-14}m)^2} \\[5pt] &= 3.28 \times 10^{−13}J \\[5pt] &= 2.05 \, MeV \end{align*} \nonumber \]
Le premier état excité :
\[E_2 = 2^2 E_1 = 4(2.05 \, MeV) = 8.20 \, MeV. \nonumber \]
L'énergie du photon émis est
\[E_f = \Delta E = E_2 - E_1 = 8.20 \, MeV - 2.05 \, MeV = 6.15 \, MeV. \nonumber \]
La fréquence du photon émis est
\[f = \dfrac{E_f}{h} = \dfrac{6.15 \, MeV}{4.14 \times 10^{-21}MeV \cdot s} = 1.49 \times 10^{21} Hz. \nonumber \]
L'importance
Il s'agit de la fréquence typique d'un rayon gamma émis par un noyau. L'énergie de ce photon est environ 10 millions de fois supérieure à celle d'un photon de lumière visible.
La valeur attendue de la position d'une particule dans une boîte est donnée par
\[\langle x \rangle = \int_0^L dx \,\psi_n^* (x) x \psi_n(x) = \int_0^L dx\,x|\psi_n^*(x)|^2 = \int_0^L dx\,x \dfrac{2}{L}sin^2 \, \dfrac{nπx}{L} = \dfrac{L}{2}. \label{7.47} \]
Nous pouvons également trouver la valeur attendue de la quantité de mouvement ou de la quantité moyenne de mouvement d'un grand nombre de particules dans un état donné :
\[\begin{align} \langle p \rangle &= \int_0^L dx\psi_n^* (x) \left[-i\hbar \dfrac{d}{dx} \psi_n(x)\right] \label{7.48} \\[5pt] &= -i\hbar \int_0^L dx \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{d}{dx} \sqrt{\dfrac{2}{L}} \, \sin \, \dfrac{n\pi x}{L}\right] \\[5pt] &= -i \dfrac{2\hbar}{L} \int_0^L dx \, \sin \, \dfrac{n\pi x}{L} \left[ \dfrac{n\pi}{L} \, \cos \, \dfrac{n\pi x}{L}\right] \\[5pt] &= - i\dfrac{2n\pi \hbar}{L^2} \int_0^L dx \dfrac{1}{2} \sin \, \dfrac{2n\pi x}{L} \\[5pt] &= -i \dfrac{n\pi \hbar}{L^2} \dfrac{L}{2n\pi} \int_0^{2\pi n} d\varphi \, \sin \, \varphi \\[5pt] &= -i \dfrac{\hbar}{2L} \cdot 0 \\[5pt] &= 0. \end{align} \]
Ainsi, pour une particule dans un état d'énergie défini, la position moyenne se trouve au milieu de la boîte et la quantité de mouvement moyenne de la particule est nulle, comme ce serait également le cas pour une particule classique. Notez que si l'énergie minimale d'une particule classique peut être nulle (la particule peut être au repos au milieu de la boîte), l'énergie minimale d'une particule quantique n'est pas nulle et est donnée par l'équation \ ref {7.44}. L'énergie moyenne des particules dans le nième état quantique, c'est-à-dire sa valeur d'énergie attendue, est
\[E_n = \langle E \rangle = n^2 \dfrac{\pi^2 \hbar^2}{2m}. \label{7.49} \]
Le résultat n'est pas surprenant car l'état d'onde stationnaire est un état d'énergie définie. Toute mesure d'énergie de ce système doit renvoyer une valeur égale à l'une de ces énergies autorisées.
Notre analyse de la particule quantique contenue dans une boîte ne serait pas complète sans discuter du principe de correspondance de Bohr. Ce principe indique que pour les grands nombres quantiques, les lois de la physique quantique doivent donner des résultats identiques à ceux de la physique classique. Pour illustrer le fonctionnement de ce principe pour une particule quantique dans une boîte, nous tracons la distribution de densité de probabilité
\[|\psi_n(x)|^2 = \dfrac{2}{L} sin^2 (n\pi x/L) \label{7.50} \]
pour trouver la particule à proximité de l'emplacement\(x\) entre les parois lorsque la particule est à l'état quantique\(\psi_n\). La figure\(\PageIndex{3}\) montre ces distributions de probabilité pour l'état fondamental, pour le premier état excité et pour un état hautement excité qui correspond à un grand nombre quantique. Ces diagrammes montrent que lorsqu'une particule quantique se trouve à l'état fondamental, elle est plus susceptible de se trouver au milieu de la boîte, là où la distribution de probabilité a la plus grande valeur. Ce n'est pas le cas lorsque la particule est dans le premier état excité, car maintenant la distribution de probabilité a la valeur zéro au milieu de la boîte, il n'y a donc aucune chance d'y trouver la particule. Lorsqu'une particule quantique se trouve dans le premier état excité, la distribution de probabilité comporte deux maxima, et les meilleures chances de trouver la particule se situent à des positions proches des emplacements de ces maxima. Cette image quantique est différente de l'image classique.
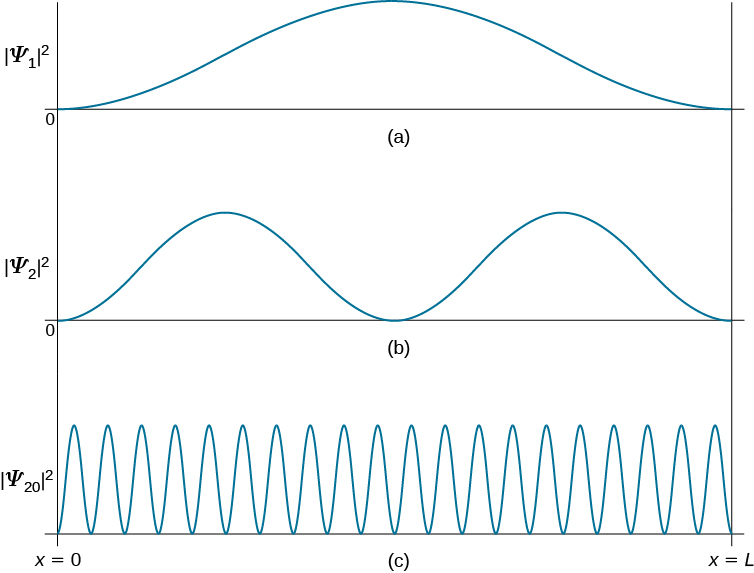
La densité de probabilité de trouver une particule classique entre\(x\) et\(x + \Delta x\) dépend du temps que\(Δt\) la particule passe dans cette région. En supposant que sa vitesse u est constante, ce temps l'est\(Δt = Δx/u\), qui est également constant pour tout endroit entre les parois. Par conséquent, la densité de probabilité de trouver la particule classique à\(x\) est uniforme dans l'ensemble de la boîte, et il n'y a aucun emplacement préférable pour trouver une particule classique. Cette image classique correspond à la limite des grands nombres quantiques. Par exemple, lorsqu'une particule quantique est dans un état hautement excité, comme le montre la figure\(\PageIndex{3}\), la densité de probabilité est caractérisée par des fluctuations rapides, puis la probabilité de trouver la particule quantique dans l'intervalle Δx ne dépend pas de l'emplacement de cet intervalle entre les parois.
Un petit chariot de 0,40 kg fait des allers-retours le long d'une voie d'aération entre deux pare-chocs situés à 2,0 m l'un de l'autre. Nous supposons qu'il n'y a pas de friction ; les collisions avec les pare-chocs sont parfaitement élastiques, de sorte qu'entre les pare-chocs, la voiture maintient une vitesse constante de 0,50 m/s. En traitant le chariot comme une particule quantique, estimez la valeur du nombre quantique principal qui correspond à son énergie classique.
Stratégie
Nous trouvons l'énergie cinétique K du chariot et son énergie fondamentale\(E_1\) comme s'il s'agissait d'une particule quantique. L'énergie du chariot est complètement cinétique, donc\(K = n^2 E_1\) (Équation \ ref {7.45}). Résoudre pour n donne\(n = (K/E_1)^{1/2}\).
Solution
L'énergie cinétique du chariot est
\[K = \dfrac{1}{2} mu^2 = \dfrac{1}{2}(0.40 \, kg)(0.50 \, m/s)^2 = 0.050 \, J. \nonumber \]
L'état fondamental du chariot, traité comme une particule quantique, est
\[E_1 = \dfrac{\pi^2 \hbar^2}{2mL^2} = \dfrac{\pi^2 (1.05 \times 10^{-34} J \cdot s)^2}{2(0.40 \, kg)(2.0 \, m)^2} = 1.700 \times 10^{-68} J. \nonumber \]
Par conséquent,\[n = (K/E_1)^{1/2} = (0.050/1.700 \times 10^{-68})^{1/2} = 1.2 \times 10^{33}. \nonumber \]
L'importance
Nous voyons dans cet exemple que l'énergie d'un système classique est caractérisée par un très grand nombre quantique. Le principe de correspondance de Bohr concerne ce type de situation. Nous pouvons appliquer le formalisme de la mécanique quantique à tout type de système, quantique ou classique, et les résultats sont corrects dans chaque cas. Dans la limite des nombres quantiques élevés, il n'y a aucun avantage à utiliser le formalisme quantique, car nous pouvons obtenir les mêmes résultats avec le formalisme moins complexe de la mécanique classique. Cependant, nous ne pouvons pas appliquer le formalisme classique à un système quantique dans un état d'énergie à faible nombre.
(a) Considérez un puits carré infini avec des limites murales\(x=0\) et\(x=L\). Quelle est la probabilité de trouver une particule quantique dans son état fondamental entre\(x=0\) et\(x=L/4\) ? (b) Répétez la question (a) pour une particule classique.
Solution
a. 9,1 % ; b. 25 %
Après avoir trouvé les états stationnaires\(ψ_n(x)\) et les énergies\(E_n\) en résolvant l'équation de SchrDinger indépendante du temps (Équation \ ref {7.32}), nous utilisons l'équation 7.4.12 pour écrire des fonctions d'onde\(Ψ_n(x,t)\) qui sont des solutions de l'équation de SchrDinger dépendante du temps donnée par l'équation 7.4.7. Pour une particule dans une boîte, cela donne
\[\Psi_n(x,t) = e^{-i\omega_nt} \psi_n(x) = \sqrt{\dfrac{2}{L}}e^{-iE_nt/\hbar}sin \, \dfrac{n\pi x}{L}, \, n = 1,2,3,... \label{7.51} \]
où les énergies sont données par l'équation \ ref {7.41}.
Le modèle de particules quantiques dans une boîte a des applications pratiques dans un domaine relativement récent de l'optoélectronique, qui traite des dispositifs qui convertissent des signaux électriques en signaux optiques. Ce modèle traite également de phénomènes physiques à l'échelle nanométrique, tels qu'une nanoparticule piégée dans un faible potentiel électrique délimitée par des barrières à potentiel élevé.


