5.10 : Énergie relativiste
- Page ID
- 189703
À la fin de cette section, vous serez en mesure de :
- Expliquer comment le théorème de l'énergie travail-énergie conduit à une expression de l'énergie cinétique relativiste d'un objet
- Montrez comment l'énergie relativiste est liée à l'énergie cinétique classique et fixe une limite à la vitesse de tout objet ayant une masse
- Décrire comment l'énergie totale d'une particule est liée à sa masse et à sa vitesse
- Expliquer comment la relativité est liée à l'équivalence énergie-masse et certaines des implications pratiques de l'équivalence énergie-masse
Le tokamak de la figure\(\PageIndex{1}\) est une forme de réacteur de fusion expérimental, qui peut transformer la masse en énergie. Les réacteurs nucléaires sont la preuve de la relation entre l'énergie et la matière.

La conservation de l'énergie est l'une des lois les plus importantes de la physique. Non seulement l'énergie a de nombreuses formes importantes, mais chaque forme peut être convertie en une autre. Nous savons que, de façon classique, la quantité totale d'énergie d'un système reste constante. Relativement, l'énergie est toujours conservée, mais l'équivalence énergie-masse doit désormais être prise en compte, par exemple, dans les réactions qui se produisent au sein d'un réacteur nucléaire. L'énergie relativiste est intentionnellement définie de manière à être conservée dans tous les cadres inertiels, comme c'est le cas pour le moment relativiste. En conséquence, plusieurs grandeurs fondamentales sont liées d'une manière inconnue en physique classique. Toutes ces relations ont été vérifiées par des résultats expérimentaux et ont des conséquences fondamentales. La nouvelle définition de l'énergie contient certaines des nouvelles connaissances les plus fondamentales et les plus spectaculaires de l'histoire récente sur la nature.
Énergie cinétique et limite de vitesse ultime
Le premier postulat de la relativité indique que les lois de la physique sont les mêmes dans tous les cadres inertiels. Einstein a montré que la loi de conservation de l'énergie d'une particule est valide sur le plan relativiste, sauf pour l'énergie exprimée en termes de vitesse et de masse d'une manière compatible avec la relativité. Considérons d'abord l'expression relativiste de l'énergie cinétique. Nous utilisons à nouveau la vitesse\(u\) pour la distinguer de la vitesse relative\(v\) entre les observateurs. Classiquement, l'énergie cinétique est liée à la masse et à la vitesse par l'expression familière
\[K = \dfrac{1}{2} mu^2. \nonumber \]
L'expression relativiste correspondante pour l'énergie cinétique peut être obtenue à partir du théorème de l'énergie de travail. Ce théorème indique que le réseau d'un système passe en énergie cinétique. Plus précisément, si une force, exprimée comme
\[\vec{F} = \dfrac{d\vec{p}}{dt} = m\dfrac{d(\gamma \vec{u})}{dt} \nonumber \]
accélère une particule du repos à sa vitesse finale, le travail effectué sur la particule doit être égal à son énergie cinétique finale. Sous forme mathématique, pour un mouvement unidimensionnel :
\[\begin{align*} K &= \int Fdx = \int m \dfrac{d}{dt} (\gamma u) dx \nonumber \\[4pt] &= m \int \dfrac{d(\gamma u)}{dt} \dfrac{dx}{dt} \\[4pt] &= m \int u \dfrac{d}{dt} \left( \dfrac{u}{\sqrt{1 - (u/c)^2}}\right) dt. \end{align*} \nonumber \]
Intégrez cela par pièces pour obtenir
\[\begin{align*} K &= \left. \dfrac{mu^2}{\sqrt{1 - (u/c)^2}}\right|_{0}^{u} - m\int \dfrac{u}{\sqrt{1 - (u/c)^2}}\dfrac{du}{dt}dt \\[4pt] &= \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - m\int \dfrac{u}{\sqrt{1 - (u/c)^2}}du \\[4pt] &= \left. \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - mc^2 (\sqrt{1 - (u/c)^2})\right|_0^u \\[4pt] &= \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} + \dfrac{mu^2}{\sqrt{1 - (u/c)^2}} - m c^2 \\[4pt] &= mc^2 \left[ \dfrac{(u^2/c^2) + 1 - (u^2/c^2)}{\sqrt{1 - (u/c)^2}}\right] - mc^2 \nonumber \\[4pt] &= \dfrac{mc^2}{\sqrt{1 - (u/c)^2}} - mc^2. \end{align*} \nonumber \]
Par conséquent, l'énergie cinétique relativiste de toute particule de masse\(m\) est
\[K_{rel} = (\gamma - 1)mc^2. \label{RKE} \]
Lorsqu'un objet est immobile, sa vitesse est\(u = 0\) et
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}} = 1 \nonumber \]
de sorte qu'\(K_{rel} = 0\)au repos, comme prévu. Cependant, l'expression de l'énergie cinétique relativiste (telle que l'énergie totale et l'énergie de repos) ne ressemble pas beaucoup à la classique\(\dfrac{1}{2} mu^2\). Pour montrer que l'expression pour\(K_{rel}\) réduire est l'expression classique de l'énergie cinétique à basse vitesse, nous utilisons l'expansion binomiale pour obtenir une approximation\((1 + ε)^n\) valide pour les petites\(ε\) :
\[(1 + ε)^n = 1 + nε + \dfrac{n(n−1)}{2!}ε^2 + \dfrac{n(n−1)(n−2)}{3!}ε^3 +⋯ ≈ 1 + nε \nonumber \]
en négligeant les très faibles termes\(ε^2\) et les pouvoirs supérieurs de\(ε\). Choisir\(ε = −u^2/c^2\) et\(n = -\dfrac{1}{2}\) conduit à la conclusion qu'\(\gamma\)à des vitesses non relativistes, où\(ε = u/c\) est faible, satisfait
\[\gamma = (1 - u^2/c^2)^{-1/2} \approx 1 + \dfrac{1}{2} \left( \dfrac{u^2}{c^2}\right). \nonumber \]
Une expansion binomiale est une façon d'exprimer une quantité algébrique sous la forme de la somme d'une série infinie de termes. Dans certains cas, comme dans la limite de la petite vitesse ici, la plupart des termes sont très petits. Ainsi, l'expression dérivée ici pour n'\(\gamma\)est pas exacte, mais il s'agit d'une approximation très précise. Par conséquent, à basse vitesse :
\[\gamma - 1 \approx \dfrac{1}{2} \left(\dfrac{u^2}{c^2}\right). \nonumber \]
En saisissant cela dans l'expression de l'énergie cinétique relativiste (équation \ ref {RKE}), vous obtenez
\[\begin{align*} K_{rel} &\approx \left[\dfrac{1}{2}\left( \dfrac{u^2}{c^2}\right)\right] mc^2 \\[4pt] &\approx \dfrac{1}{2} mu^2 \\[4pt] &\approx K_{class}. \end{align*} \nonumber \]
C'est-à-dire que l'énergie cinétique relativiste devient la même que l'énergie cinétique classique lorsque\(u \ll c\).
Il est encore plus intéressant d'étudier ce qu'il advient de l'énergie cinétique lorsque la vitesse d'un objet se rapproche de celle de la lumière. Nous savons que cela\(\gamma\) devient infini à mesure que l'on\(u\) approche\(c\), de sorte qu'il devient\(K_{rel}\) également infini lorsque la vitesse se rapproche de la vitesse de la lumière (Figure\(\PageIndex{2}\)). L'augmentation\(K_{rel}\) est bien plus importante que celle qui\(K_{class}\)\(v\) s'approche\(c\). Une quantité infinie de travail (et donc une quantité infinie d'énergie) est nécessaire pour accélérer une masse à la vitesse de la lumière.
Aucun objet ayant une masse ne peut atteindre la vitesse de la lumière.
La vitesse de la lumière est la limite de vitesse ultime pour toute particule ayant une masse. Tout cela est conforme au fait que les vitesses inférieures à c s'additionnent toujours à moins de\(c\). La forme relativiste de l'énergie cinétique et la limite de vitesse ultime\(c\) ont été confirmées en détail dans de nombreuses expériences. Quelle que soit la quantité d'énergie investie pour accélérer une masse, sa vitesse ne peut que s'approcher de la vitesse de la lumière, et non l'atteindre.
Un électron a une vitesse\(v = 0.990 c\).
- Calculez l'énergie cinétique en MeV de l'électron.
- Comparez cette valeur à la valeur classique de l'énergie cinétique à cette vitesse. (La masse d'un électron est de\(9.11 \times 10^{-31}kg\).)
Stratégie
L'expression de l'énergie cinétique relativiste est toujours correcte, mais pour (a), elle doit être utilisée car la vitesse est hautement relativiste (proche de\(c\)). Nous calculons d'abord le facteur relativiste\(\gamma\), puis nous l'utilisons pour déterminer l'énergie cinétique relativiste. Pour (b), nous calculons l'énergie cinétique classique (qui serait proche de la valeur relativiste si elle\(v\) était inférieure à quelques pour cent de\(c\)) et nous constatons qu'elle n'est pas la même.
Solution pour (a)
- Identifier les éléments connus :\(v = 0.990c\)\(m = 9.11 \times 10^{-31}kg\)
- Identifiez l'inconnu :\(K_{rel}\).
- Exprimez la réponse sous forme d'équation :\(K_{rel} = (\gamma - 1)mc^2\) avec\(\gamma = \dfrac{1}{\sqrt{1 - u^2/c^2}}.\)
- Fais le calcul. Commencez par calculer\(\gamma\). Gardez des chiffres supplémentaires car il s'agit d'un calcul intermédiaire : utilisez\[\begin{align*} \gamma &= \dfrac{1}{\sqrt{1 - u^2/c^2}} \nonumber \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{(0.990c)^2}{c^2}}} \nonumber \\[4pt] &= 7.0888. \end{align*} \nonumber \] maintenant cette valeur pour calculer l'énergie cinétique (Equatoin \ ref {RKE}) :
\[\begin{align*} K_{rel} &= (\gamma - 1)mc^2 \nonumber \\[4pt] &= (7.0888 - 1)(9.11 \times 10^{-31}\, kg)(3.00 \times 10^8\, m/s^2) \nonumber \\[4pt] &= 4.9922 \times 10^{−13}\, J \end{align*} \nonumber \]
- Convertir les unités :
\[\begin{align*} K_{rel} &= (4.9922 \times 10^{−13}\, J) \left(\dfrac{1\, MeV}{1.60 \times 10^{−13} J}\right) \\[4pt] &= 3.12\, MeV.\end{align*} \nonumber \]
Solution pour (b)
- Énumérez les connus :\(v = 0.990c\) ;\(m = 9.11 \times 10^{−31}kg\).
- Listez l'inconnu :\(K_{rel}\)
- Exprimez la réponse sous forme d'équation :
- Effectuez le calcul :
\[\begin{align*} K_{class} &= \dfrac{1}{2} mu^2 \\[4pt] &= \dfrac{1}{2} (9.11 \times 10^{-31} kg)(0.990)^2(3.00 \times 10^8\, m/s)^2 \\[4pt] &= 4.0179 \times 10^{−14}J.\end{align*} \nonumber \]
- Convertir les unités :
\[\begin{align*} K_{class} &= 4.0179 \times 10^{-14} J \left(\dfrac{1\, MeV}{1.60 \times 10^{-13} J}\right) \\[4pt] &= 0.251\, MeV.\end{align*} \nonumber \]
L'importance
Comme on pouvait s'y attendre, étant donné que la vitesse est de 99,0 % de la vitesse de la lumière, l'énergie cinétique classique diffère significativement de la valeur relativiste correcte. Notez également que la valeur classique est beaucoup plus petite que la valeur relativiste. En fait,\(K_{rel}/K_{class} = 12.4\) dans ce cas. Cela montre à quel point il est difficile de déplacer une masse à une vitesse proche de celle de la lumière. Il faut beaucoup plus d'énergie que prévu de façon classique. Des quantités d'énergie toujours plus importantes sont nécessaires pour rapprocher la vitesse d'une masse de celle de la lumière. Une énergie de 3 MeV est une très petite quantité pour un électron, et elle peut être atteinte avec les accélérateurs de particules actuels. Le SLAC, par exemple, peut accélérer les électrons vers le dessus\(50 \times 10^9 eV = 50,000\, MeV\).
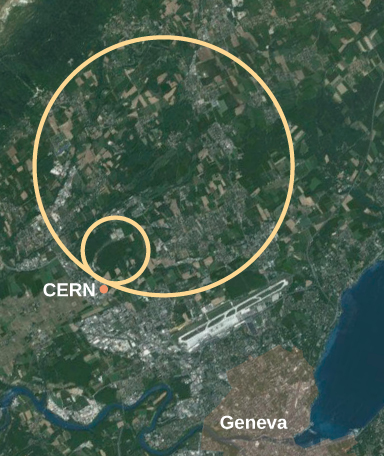
Est-il utile de rapprocher v un peu plus de c que 99,0 % ou 99,9 % ? La réponse est oui. Nous apprenons beaucoup de choses en faisant cela. L'énergie qui entre dans une masse à haute vitesse peut être convertie sous n'importe quelle autre forme, y compris en particules entièrement nouvelles. Dans le Grand collisionneur de hadrons de la figure\(\PageIndex{1}\), les particules chargées sont accélérées avant de pénétrer dans la structure annulaire. Deux faisceaux de particules y sont accélérés jusqu'à leur vitesse finale d'environ 99,7 % de la vitesse de la lumière dans des directions opposées, puis ils entrent en collision, produisant des espèces de particules totalement nouvelles. La plupart de ce que nous savons sur la sous-structure de la matière et la collection de particules exotiques à courte durée de vie dans la nature a été appris de cette manière. L'évolution des caractéristiques de ces particules jusqu'alors inconnues suggère l'existence d'une sous-structure de base pour toute la matière. Ces particules et certaines de leurs caractéristiques seront abordées dans un chapitre ultérieur sur la physique des particules.
Énergie relativiste totale
L'expression de l'énergie cinétique peut être réarrangée comme suit :
\[\begin{align*} E &= \dfrac{mc^2}{\sqrt{1 - u^2/c^2}} \\[4pt] &= K + mc^2. \end{align*} \nonumber \]
Einstein a soutenu dans un article distinct, également publié plus tard en 1905, que si l'énergie d'une particule change\(\Delta E\), sa masse change de\(\Delta m = \Delta E/C^2\). De nombreuses preuves expérimentales depuis lors confirment que cela\(mc^2\) correspond à l'énergie que\(m\) possède la particule de masse au repos. Par exemple, lorsqu'un pion de masse neutre\(m\) au repos se désintègre en deux photons, les photons ont une masse nulle mais on observe que leur énergie totale correspond\(mc^2\) à celle du pion. De même, lorsqu'une particule de masse se\(m\) désintègre en deux ou plusieurs particules ayant une masse totale plus faible, l'énergie cinétique observée transmise aux produits de la désintégration correspond à la diminution de masse. C'\(E\)est donc l'énergie relativiste totale de la particule et\(mc^2\) son énergie de repos.
L'énergie totale (\(E\)) d'une particule est
\[E = \gamma mc^2 \nonumber \]
où\(m\) est la masse,\(c\) la vitesse de la lumière et\(u\) la vitesse de la masse par rapport à un observateur.\(\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}}\)
L'énergie de repos d'un objet est
\[E_0 = mc^2. \label{rest energy} \]
L'équation \ ref {énergie de repos} est la forme correcte de la plus célèbre équation d'Einstein, qui montre pour la première fois que l'énergie est liée à la masse d'un objet au repos. Par exemple, si de l'énergie est stockée dans l'objet, sa masse de repos augmente. Cela implique également que la masse peut être détruite pour libérer de l'énergie. Les implications de ces deux premières équations concernant l'énergie relativiste sont si vastes qu'elles n'ont pas été complètement reconnues pendant quelques années après leur publication par Einstein en 1905, et la preuve expérimentale de leur exactitude n'a pas été largement reconnue au début. Il convient de noter qu'Einstein a compris et décrit les significations et les implications de sa théorie.
Calculez l'énergie restante d'une masse de 1,00 g.
Stratégie
Un gramme est une petite masse, soit moins de la moitié de la masse d'un cent. Nous pouvons multiplier cette masse, en unités SI, par la vitesse de la lumière au carré pour trouver l'énergie de repos équivalente.
Solution
- Identifiez les connus :\(m = 1.00 \times 10^{-3} kg\) ;\(c = 3.00 \times 10^8 m/s\).
- Identifiez l'inconnu :\(E_0\).
- Exprimez la réponse sous forme d'équation :\(E_0 = mc^2\).
- Effectuez le calcul :
\[E_0 = mc^2 = (1.00 \times 10^{-3} kg) (3.00 \times 10^8 m/s)^2 = 9.00 \times 10^{13} kg \cdot m^2/s^2. \nonumber \]
- Convertissez les unités. En constatant cela\(1\, kg \cdot m^2/s^2 = 1\, J\), nous voyons que l'énergie restante est la suivante :
\[E_0 = 9.00 \times 10^{13}\, J. \nonumber \]
L'importance
C'est une énorme quantité d'énergie pour une masse de 1 g. L'énergie de repos est importante parce que la vitesse de la lumière c est un nombre élevé et\(c^2\) un très grand nombre, donc c'\(mc^2\)est énorme pour n'importe quelle masse macroscopique. L'énergie massique\(9.00 \times 10^{13} J\) restante pour 1,00 g est environ le double de l'énergie libérée par la bombe atomique d'Hiroshima et environ 10 000 fois l'énergie cinétique d'un grand porte-avions.
Aujourd'hui, les applications pratiques de la conversion de masse en une autre forme d'énergie, comme dans les armes nucléaires et les centrales nucléaires, sont bien connues. Mais des exemples existaient également lorsqu'Einstein a proposé pour la première fois la forme correcte d'énergie relativiste, et il a décrit certaines d'entre elles. Des radiations nucléaires ont été découvertes au cours de la décennie précédente et l'origine de leur énergie reste un mystère. Cela s'explique par le fait que, dans certains processus nucléaires, une petite quantité de masse est détruite et de l'énergie est libérée et transportée par les radiations nucléaires. Mais la quantité de masse détruite est si faible qu'il est difficile de détecter qu'il en manque. Bien qu'Einstein ait proposé cette source d'énergie dans les sels radioactifs alors étudiés, il a fallu de nombreuses années avant que l'on reconnaisse largement que la masse pouvait être convertie en énergie et, en fait, l'est généralement (Figure\(\PageIndex{4}\)).

En raison de la relation entre l'énergie de repos et la masse, nous considérons maintenant la masse comme une forme d'énergie plutôt que comme quelque chose de distinct. Il n'y avait même pas eu la moindre trace de cela avant l'œuvre d'Einstein. L'équivalence énergie-masse est maintenant connue pour être la source de l'énergie solaire, l'énergie de la désintégration nucléaire et même l'une des sources d'énergie qui maintiennent la chaleur intérieure de la Terre.
Énergie stockée et énergie potentielle
Qu'advient-il de l'énergie stockée dans un objet au repos, telle que l'énergie injectée dans une batterie en la chargeant ou l'énergie stockée dans le ressort comprimé d'un pistolet jouet ? L'apport d'énergie fait partie de l'énergie totale de l'objet et augmente ainsi sa masse au repos. Toute l'énergie stockée et potentielle devient une masse dans un système. Apparemment contradictoire, le principe de conservation de la masse (c'est-à-dire que la masse totale est constante) était l'une des grandes lois vérifiées par la science du XIXe siècle. Pourquoi n'a-t-on pas remarqué que c'était incorrect ? L'exemple suivant permet de répondre à cette question.
Une batterie de voiture est conçue pour être capable de déplacer 600 ampères-heures\((A \cdot h)\) de charge à 12,0 V.
- Calculez l'augmentation de la masse au repos d'une telle batterie lorsqu'elle passe d'une batterie complètement déchargée à une charge complète, en supposant qu'aucun réactif chimique n'entre dans la batterie ou n'en sort.
- Quel est ce pourcentage d'augmentation, étant donné que la masse de la batterie est de 20,0 kg ?
Stratégie
Dans la partie (a), nous devons d'abord trouver l'énergie stockée sous forme d'énergie chimique\(E_{batt}\) dans la batterie, qui est égale à l'énergie électrique que la batterie peut fournir. Parce que\(E_{batt} = qV\) nous devons calculer la charge\(q\) entrante\(600\, A \cdot h\), qui est le produit du courant\(I\) et du temps\(t\). Nous multiplions ensuite le résultat par 12,0 V. Nous pouvons ensuite calculer l'augmentation de masse de la batterie en utilisant\(E_{batt} = (\Delta m)c^2\). La partie (b) est un ratio simple converti en pourcentage.
Solution pour (a)
- Identifiez les éléments connus :\[I \cdot t = 600\, A \cdot h;\, V = 12.0\, V;\, c = 3.00 \times 10^8\, m/s. \nonumber \]
- Identifiez l'inconnu :\(\Delta m\).
- Exprimez la réponse sous forme d'équation :\[\begin{align*} E_{batt} &= (\Delta m)c^2 \\[4pt] \Delta m &= \dfrac{E_{batt}}{c^2} \\[4pt] &= \dfrac{qV}{c^2} \\[4pt] &= \dfrac{(It)V}{c^2}.\end{align*} \nonumber \]
- Effectuez le calcul :\[\Delta m = \dfrac{(600\, A \cdot h)(12.0\, V)}{(3.00 \times 10^8)^2}. \nonumber \]
- Écrivez les ampères A sous forme de coulombs par seconde (C/s) et convertissez les heures en secondes :
\[\begin{align*}\Delta m &= \dfrac{(600\, C/s \cdot h)\left(\dfrac{3600\, s}{1\, h}\right)(12.0\, J/C)}{(3.00 \times 10^8\, m/s)^2} \\[4pt] &= 2.88 \times 10^{-10}\, kg. \end{align*} \nonumber \]
où nous avons utilisé la conversion\(1\, kg \cdot m^2/s^2 = 1\, J.\).
Solution pour (b)
Pour la partie (b) :
- Identifiez les connus :\(\delta m = 2.88 \times 10^{-10}kg\) ;\(m = 20.0\, kg\).
- Identifiez l'inconnu : % de variation.
- Exprimez la réponse sous forme d'équation :\[\%\, increase = \dfrac{\delta m}{m} \times 100\%. \nonumber \]
- Effectuez le calcul :
\[\begin{align*} \%\, increase &= \dfrac{\Delta m}{m} \times 100\% \\[4pt] &= \dfrac{2.88 \times 10^{-10}\, kg}{20.0\, kg} \times 100\% \\[4pt] &= 1.44 \times 10^{-9} \% \end{align*} \nonumber \]
L'importance
L'augmentation réelle de la masse et le pourcentage d'augmentation sont très faibles, car l'énergie est divisée par\(c^2\) un très grand nombre. Il faudrait être capable de mesurer la masse de la batterie avec une précision d'un milliardième de pour cent, soit une partie\(10^{11}\), pour constater cette augmentation. Il n'est pas étonnant que la variation de masse ne soit pas facilement observée. En fait, ce changement de masse est si faible que l'on peut se demander comment quelqu'un pourrait vérifier qu'il est réel. La réponse se trouve dans les processus nucléaires dans lesquels le pourcentage de masse détruite est suffisamment important pour être mesuré avec précision. La masse du combustible d'un réacteur nucléaire, par exemple, est sensiblement plus faible lorsque son énergie a été utilisée. Dans ce cas, l'énergie stockée a été libérée (convertie principalement en énergie thermique pour alimenter des générateurs électriques) et la masse restante a diminué. L'utilisation de l'énergie stockée dans une batterie entraîne également une diminution de la masse, sauf que l'énergie stockée est beaucoup plus importante dans les processus nucléaires, ce qui rend la variation de masse mesurable en pratique et en théorie.
Énergie et élan relativistes
Nous savons classiquement que l'énergie cinétique et la quantité de mouvement sont liées l'une à l'autre, car :
\[K_{class} = \dfrac{p^2}{2m} = \dfrac{(mu)^2}{2m} = \dfrac{1}{2}mu^2. \nonumber \]
Sur le plan relativiste, nous pouvons obtenir une relation entre l'énergie et le moment en manipulant algébriquement leurs équations qui les définissent. Cela donne :
\[E^2 = (pc)^2 + (mc^2)^2, \label{5.11} \]
où\(E\) est l'énergie totale relativiste,
\[E = \dfrac{mc^2 }{\sqrt{1 - u^2/c^2}} \nonumber \]
et\(p\) c'est l'élan relativiste. Cette relation entre l'énergie relativiste et l'élan relativiste est plus compliquée que la version classique, mais nous pouvons acquérir de nouvelles connaissances intéressantes en l'examinant. Premièrement, l'énergie totale est liée à la quantité de mouvement et à la masse au repos. Au repos, le moment est nul et l'équation donne à l'énergie totale l'énergie de repos\(mc^2\) (cette équation est donc cohérente avec la discussion sur l'énergie de repos ci-dessus). Cependant, à mesure que la masse est accélérée, sa quantité de mouvement\(p\) augmente, augmentant ainsi l'énergie totale. À des vitesses suffisamment élevées, le terme d'énergie de repos\((mc^2)^2\) devient négligeable par rapport au terme de quantité de mouvement\((pc)^2\) ; donc,\(E = pc\) à des vitesses extrêmement relativistes.
Si nous considérons que\(p\) la quantité de mouvement est distincte de la masse, nous pouvons déterminer les implications de l'équation
\[E^2 = (pc)^2 + (mc^2)^2, \nonumber \]
pour une particule qui n'a pas de masse. Si nous prenons\(m\) pour zéro dans cette équation, alors\(E = pc,\, orp = E/c\). Les particules sans masse ont cet élan. Plusieurs particules sans masse se trouvent dans la nature, notamment des photons (qui sont des paquets de rayonnement électromagnétique). Une autre implication est qu'une particule sans masse doit se déplacer à la vitesse c et uniquement à la vitesse c. Il n'entre pas dans le cadre de ce texte d'examiner en détail la relation\(E^2 = (pc)^2 + (mc^2)^2\) dans l'équation, mais vous pouvez voir que la relation a des implications importantes en matière de relativité spéciale.
Quelle est l'énergie cinétique d'un électron si sa vitesse est égale à\(0.992c\) ?
- Réponse
-
\[ \begin{align*} K_{rel} &= (\gamma - 1)mc^2 = \left(\dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}} - 1 \right) mc^2 \nonumber \\[4pt] &= \left(\dfrac{1}{\sqrt{1 - \dfrac{(0.992 c)^2}{c^2}}} - 1 \right) (9.11 \times 10^{-31}\, kg)(3.00 \times 10^8\, m/s)^2 \nonumber \\[4pt] &= 5.67 \times 10^{-13}\, J \end{align*} \nonumber \]


