5.9 : Moment relativiste

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Définir le moment relativiste en termes de masse et de vitesse
• Montrez comment l'élan relativiste est lié à l'élan classique
• Montrez comment la conservation de l'élan relativiste limite les objets ayant une masse à des vitesses inférieures à c

Le momentum est un concept central en physique. La forme la plus large de la deuxième loi de Newton est exprimée en termes de moment. La dynamique est conservée chaque fois que la force externe nette sur un système est nulle. Cela fait de la conservation de l'élan un outil fondamental pour analyser les collisions (Figure\(\PageIndex{1}\)). Une grande partie de ce que nous savons de la structure subatomique provient de l'analyse des collisions de particules relativistes produites par des accélérateurs, et la conservation de la quantité de mouvement joue un rôle crucial dans cette analyse.

Figure\(\PageIndex{1}\) : Momentum est un concept important pour ces joueurs de football de l'université de Californie à Berkeley et de l'université de Californie à Davis. Un joueur ayant la même vélocité mais une masse plus importante entre en collision avec un impact plus important car son élan est plus important. Pour les objets se déplaçant à des vitesses relativistes, l'effet est encore plus important.

Le premier postulat de la relativité indique que les lois de la physique sont les mêmes dans tous les cadres inertiels. La loi de conservation de l'élan survivt-elle à cette exigence à des vitesses élevées ? Il peut être démontré que la quantité de mouvement calculée simplement\(\vec{p} = m\frac{d\vec{x}}{dt}\), même si elle est conservée dans un cadre de référence, peut ne pas être conservée dans un autre après application de la transformation de Lorentz aux vitesses. On peut plutôt montrer que l'équation correcte pour la quantité de mouvement est l'expression classique en termes d'incrément dτ du temps propre de la particule, observé dans le cadre de repos de la particule :

\[\begin{align*} \vec{p} &= m\frac{d\vec{x}}{dτ} = m\frac{d\vec{x}}{dt} \frac{dt}{d\tau} \\[5pt] &= m\frac{d\vec{x}}{dt}\frac{1}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \frac{m\vec{u}}{\sqrt{1 - u^2/c^2}} \\[5pt] &= \gamma m\vec{u}.\end{align*} \nonumber \]

Définition : Moment relativiste et masse de repos

L'élan relativiste\(\vec{p}\) est le moment classique multiplié par le facteur relativiste\(\gamma\) :

\[\vec{p} = \gamma m\vec{u} \label{Rmomentum} \]

où\(m\) est la masse restante de l'objet,\(\vec{u}\) sa vitesse par rapport à un observateur et\(γ\) est le facteur relativiste :

\[\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}. \label{Rmass} \]

Notez que nous utilisons ici la vitesse\(u\) pour la distinguer de la vitesse relative\(v\) entre les observateurs. Le facteur\(\gamma\) qui apparaît ici a la même forme que le facteur relativiste précédent,\(\gamma\) sauf qu'il est maintenant exprimé en termes de vitesse de la particule\(u\) au lieu de la vitesse relative v de deux référentiels.

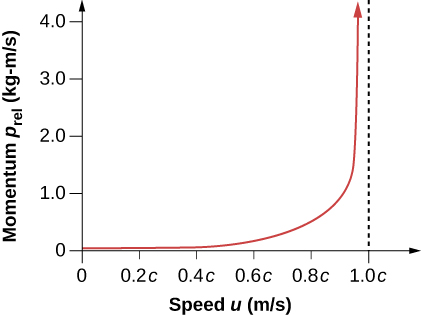
Avec p exprimé de cette manière, le moment total\(p_{tot}\) est conservé chaque fois que la force externe nette est nulle, comme en physique classique. Encore une fois, nous voyons que la quantité relativiste devient pratiquement la même que la quantité classique à basse vitesse, où elle\(u/c\)\(\gamma\) est faible et presque égale à 1. L'élan relativiste joue le même rôle intuitif que l'élan classique. Elle est plus importante pour les grandes masses se déplaçant à des vitesses élevées, mais à cause de ce facteur\(\gamma\), l'élan relativiste se rapproche de l'infini à mesure que l'on\(u\) s'approche\(c\) (Figure\(\PageIndex{2}\)). C'est une autre indication qu'un objet ayant une masse ne peut pas atteindre la vitesse de la lumière. Si c'était le cas, son élan deviendrait infini, une valeur déraisonnable.

Figure\(\PageIndex{2}\) : Le moment relativiste se rapproche de l'infini lorsque la vitesse d'un objet s'approche de la vitesse de la lumière.

Masse ou masse de repos

La définition relativiste correcte de la quantité de mouvement (équation \ ref {Rmomentum}) est parfois interprétée comme impliquant que la masse varie avec la vitesse :\(m_{var} = \gamma m\), en particulier dans les manuels plus anciens. Cependant, notez qu'\(m\)il s'agit de la masse de l'objet mesurée par une personne au repos par rapport à l'objet. Ainsi,\(m\) est définie comme étant la masse au repos, qui pourrait être mesurée au repos, peut-être par gravité. Lorsqu'une masse se déplace par rapport à un observateur, la seule façon de déterminer sa masse est d'utiliser des collisions ou d'autres moyens impliquant une quantité de mouvement. Comme la masse d'un objet en mouvement ne peut être déterminée indépendamment de la quantité de mouvement, la seule masse significative est la masse au repos. Par conséquent, lorsque nous utilisons le terme « masse », supposons qu'il est identique à « masse de repos ».

Le moment relativiste est défini de telle sorte que la conservation de la quantité de mouvement soit maintenue dans tous les cadres inertiels. Chaque fois que la force externe nette sur un système est nulle, la dynamique relativiste est conservée, comme c'est le cas pour la dynamique classique. Cela a été vérifié dans de nombreuses expériences.

Exercice\(\PageIndex{1}\)

Quelle est la quantité de mouvement d'un électron se déplaçant à une certaine vitesse\(0.985c\) ? La masse restante de l'électron est\(9.11 \times 10^{-31} kg\).

Réponse

Substituez les données dans l'équation \ ref {Rmomentum} :

\[\begin{align*} p &= \gamma mu \\[5pt] &= \frac{mu}{\sqrt{1 - \frac{u^2}{c^2}}} \\[5pt] &= \frac{(9.11 \times 10^{-31}kg)(0.985)(3.00 \times 10^8 \, m/s)}{\sqrt{1 - \frac{(0.985c)^2}{c^2}}} \\[5pt] &= 1.56 \times 10^{-21} \, kg-m/s. \end{align*} \nonumber \]