5.8 : Effet Doppler pour la lumière
- Page ID
- 189719
À la fin de cette section, vous serez en mesure de :
- Expliquer l'origine du décalage de fréquence et de longueur d'onde de la longueur d'onde observée lorsque l'observateur et la source se rapprochent ou s'éloignent l'un de l'autre
- Dériver une expression pour le décalage Doppler relativiste
- Appliquez les équations du décalage Doppler à des exemples du monde réel
Comme indiqué dans le chapitre sur le son, si une source sonore et un auditeur s'éloignent davantage, l'auditeur rencontre moins de cycles d'ondes par seconde, et donc une fréquence plus basse, que si leur séparation reste constante. Pour la même raison, l'auditeur détecte une fréquence plus élevée si la source et l'auditeur se rapprochent. Le décalage Doppler de la fréquence détectée qui en résulte se produit pour n'importe quelle forme d'onde. Pour les ondes sonores, cependant, les équations du décalage Doppler diffèrent nettement selon que c'est la source, l'observateur ou l'air qui se déplace. La lumière ne nécessite aucun support, et le décalage Doppler pour la lumière se déplaçant dans le vide dépend uniquement de la vitesse relative de l'observateur et de la source.
L'effet Doppler relativiste
Supposons qu'un observateur\(S\) voit la lumière provenant d'une source s'\(S'\)éloigner à grande vitesse\(v\) (Figure\(\PageIndex{1}\)). La longueur d'onde de la lumière peut être mesurée à l'intérieur\(S'\), par exemple en utilisant un miroir pour créer des ondes stationnaires et en mesurant la distance entre les nœuds. Ces distances sont des longueurs correctes avec\(S'\) comme base de référence, et varient d'un facteur\(\sqrt{1 - v^2/c^2}\) lorsqu'elles sont mesurées dans le cadre de l'observateur\(S\), où la règle mesurant la longueur d'onde\(S'\) est considérée comme mobile.
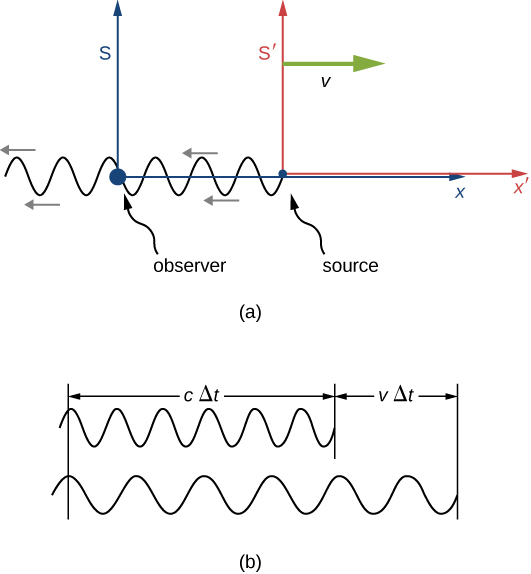
Si la source était stationnaire en S, l'observateur verrait une longueur CΔt du diagramme d'onde dans le temps Δt. Mais en raison du mouvement de S'par rapport à S, considéré uniquement dans S, l'observateur voit le diagramme d'onde, et donc la longueur d'onde, étirés par un facteur de
\[\frac{c\Delta t_{period} + v\Delta t_{period}}{c\Delta t_{period}} = 1 + \frac{v}{c} \nonumber \]
comme illustré en (b) de la figure\(\PageIndex{1}\). L'augmentation globale résultant des deux effets donne
\[\begin{align*} \lambda_{obs} &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{1 - \frac{v^2}{c^2}}} \\[4pt] &= \lambda_{src} \left(1 + \frac{v}{c}\right) \sqrt{\frac{1}{\left(1 + \frac{v}{c}\right) \left(1 - \frac{v}{c}\right)}} \\[4pt] &= \lambda_{src}\sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \end{align*} \nonumber \]
où\(\lambda_{src}\) est la longueur d'onde de la lumière vue par la source en S'et\(\lambda_{obs}\) est la longueur d'onde que l'observateur détecte dans S.
Changements de vitesse rouges et horaires bleus
La longueur d'onde observée\(λ_{obs}\) du rayonnement électromagnétique est plus longue (ce que l'on appelle « décalage vers le rouge ») que celle émise par la source lorsque la source s'éloigne de l'observateur. De même, la longueur d'onde est plus courte (ce que l'on appelle un « décalage bleu ») lorsque la source se déplace vers l'observateur. Le montant de la modification est déterminé par
\[\lambda_{obs} = \lambda_s \sqrt{\frac{\left(1 + \frac{v}{c}\right)}{\left(1 - \frac{v}{c}\right)}} \nonumber \]
où\(\lambda_s\) est la longueur d'onde dans le référentiel de la source, et\(v\) est la vitesse relative des deux trames\(S\) et\(S'\). La vitesse\(v\) est positive pour un mouvement s'éloignant d'un observateur et négative pour un mouvement vers un observateur. En termes de fréquence source et de fréquence observée, cette équation peut être écrite de la manière suivante :
\[ f_{obs} = f_s \sqrt{\frac{\left(1 - \frac{v}{c}\right)}{\left(1 + \frac{v}{c}\right)}} \label{eq20} \]
Notez que les signes sont différents de ceux de l'équation de longueur d'onde.
Supposons qu'une galaxie s'éloigne de la Terre à une vitesse de 0,825 c. Il émet des ondes radio d'une longueur d'onde de
0,525 m. Quelle longueur d'onde détecterait-on sur Terre ?
Stratégie
Comme la galaxie se déplace à une vitesse relativiste, nous devons déterminer le décalage Doppler des ondes radio en utilisant le décalage Doppler relativiste au lieu du décalage Doppler classique.
Solution
- Identifiez les connus :\(u = 0.825 c\) ;\(\lambda_s = 0.525 \, m\).
- Identifiez l'inconnu :\(\lambda_{obs}\).
- Exprimez la réponse sous forme d'équation :
\[\lambda_{obs} = \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}}. \nonumber \]
- Effectuez le calcul :
\[\begin{align*}\lambda_{obs} &= \lambda_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}} \\[4pt] &= (0.525 \, m) \sqrt{\frac{1 + \frac{0.825c}{c}}{1 - \frac{0.825c}{c}}} \\[4pt] &= 1.70 \, m. \end{align*} \nonumber \]
L'importance
Comme la galaxie s'éloigne de la Terre, nous nous attendons à ce que les longueurs d'onde du rayonnement qu'elle émet soient décalées vers le rouge. La longueur d'onde que nous avons calculée est de 1,70 m, soit décalée vers le rouge par rapport à la longueur d'onde initiale de 0,525 m. Vous verrez dans Particle Physics and Cosmology que la détection d'un rayonnement décalé vers le rouge a permis de mieux comprendre l'origine et l'évolution de l'univers aujourd'hui.
Supposons qu'une sonde spatiale s'éloigne de la Terre à une vitesse de 0,350 c. Il renvoie un message radio à la Terre à une fréquence de 1,50 GHz. À quelle fréquence le message est-il reçu sur Terre ?
Solution
Nous pouvons substituer les données directement dans l'équation de la fréquence Doppler relativiste (Équation \ ref {eq20}) :
\[\begin{align*}f_{obs} &= f_s \sqrt{\frac{1 - \frac{v}{c}}{1 + \frac{v}{c}}} \\[4pt] &= (1.50 \, GHz)\sqrt{\frac{1 - \frac{0.350c}{c}}{1 + \frac{0.350c}{c}}} \\[4pt] &= 1.04 \, GHz. \end{align*} \nonumber \]
L'effet Doppler relativiste a des applications allant de la surveillance des tempêtes par radar Doppler à la fourniture d'informations sur le mouvement et la distance des étoiles. Nous décrivons certaines de ces applications dans les exercices.


