5.7 : Transformation de vitesse relativiste
- Page ID
- 189720
À la fin de cette section, vous serez en mesure de :
- Dérivez les équations compatibles avec la relativité spéciale pour transformer les vitesses d'un référentiel inertiel en un autre.
- Appliquez les équations de transformation de vitesse aux objets se déplaçant à des vitesses relativistes.
- Examinez comment les vitesses combinées prédites par les équations de transformation relativistes se comparent à celles attendues de manière classique.
Rester en place en kayak dans une rivière au courant rapide demande des efforts. Le courant de la rivière entraîne le kayak. Essayer de pagayer à contre-courant peut déplacer le kayak vers l'amont par rapport à l'eau, mais cela ne représente qu'une partie de sa vitesse par rapport à la rive. Le mouvement du kayak est un exemple de la façon dont les vitesses se combinent en mécanique newtonienne par addition de vecteurs. La vitesse du kayak est la somme vectorielle de sa vitesse par rapport à l'eau et de la vitesse de l'eau par rapport à la rive. Cependant, l'addition relativiste des vitesses est très différente.
Transformations de vitesse
Imaginez une voiture circulant de nuit sur une route droite, comme dans la Figure\(\PageIndex{1}\). Le conducteur voit le feu quitter les phares à toute vitesse\(c\) dans le cadre de référence de la voiture. Si la transformation galiléenne s'appliquait à la lumière, la lumière des phares de la voiture s'approcherait du piéton à une certaine vitesse\(u = v + c\), contrairement aux postulats d'Einstein.
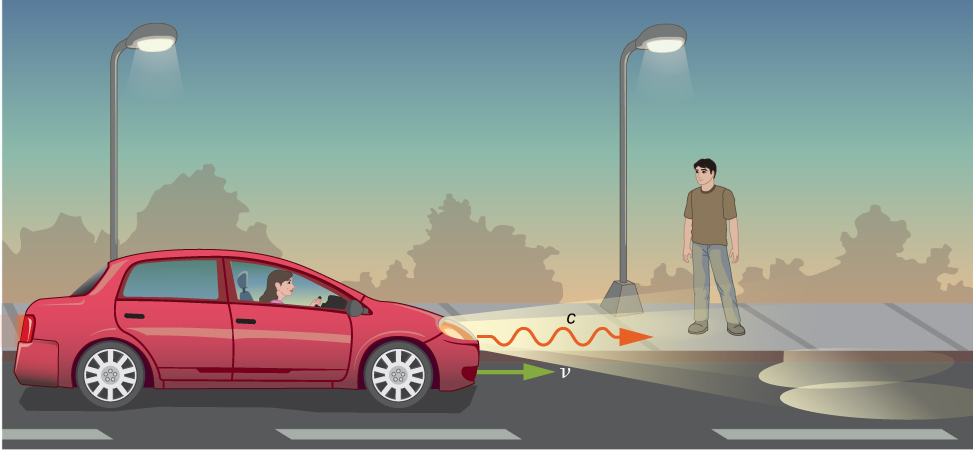
La distance parcourue et le temps de trajet sont différents dans les deux cadres de référence, et ils doivent différer de telle sorte que la vitesse de la lumière soit la même dans tous les cadres inertiels. Les règles correctes pour transformer les vitesses d'une image à l'autre peuvent être obtenues à partir des équations de transformation de Lorentz.
Transformation relativiste de la vitesse
Supposons qu'un objet P se déplace à une vitesse constante\(u = (u'_x, u'_y, u'_z)\) telle que mesurée dans le\(S'\) cadre. Le\(S'\) cadre se déplace le long de son axe x' à grande vitesse\(v\). Par incrément de temps dt', la particule est déplacée le\(dx'\) long de l'axe x'. L'application des équations de transformation de Lorentz donne les incréments de temps et de déplacement correspondants sur les axes non amorcés :
\[\begin{align} dt &= \gamma (dt' + vdx' /c^2) \\[4pt] dx &= \gamma (dx' + vdt') \\[4pt] dy &= dy' \\[4pt] dz &= dz'. \end{align} \nonumber \]
Les composantes de vitesse de la particule observées dans le système de coordonnées non amorcé sont alors
\[\begin{align} \dfrac{dx}{dt} &= \dfrac{\gamma(dx' + vdt')}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dx'}{dt'} + v}{1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}} \\[4pt] \dfrac{dy}{dt} &= \dfrac{dy'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dy'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \\[4pt] \dfrac{dz}{dt} &= \dfrac{dz'}{\gamma (dt' + v\,dx'/c^2)} = \dfrac{\dfrac{dz'}{dt'}}{\gamma \left(1 + \dfrac{v}{c^2} \dfrac{dx'}{dt'}\right)} \end{align} \nonumber \]
Nous obtenons ainsi les équations pour les composantes de vitesse de l'objet vues dans le cadre\(S\) :
\[u_x = \left(\dfrac{u'_x + v}{1 + vu'_x/c^2}\right), \, u_y = \left(\dfrac{u'_y/\gamma}{1 + vu'_x/c^2}\right), \, u_z = \left(\dfrac{u'_z/\gamma}{1 + vu'_x/c^2}\right). \nonumber \]
Comparez cela à la façon dont la transformation galiléenne de la mécanique classique indique que les vitesses se transforment, en ajoutant simplement sous forme de vecteurs :
\[u_x = u'_x + u, \, u_y = u'_y, \, u_z = u'_z. \nonumber \]
Lorsque la vitesse relative des images est bien inférieure à la vitesse de la lumière, c'est-à-dire lorsque\(v\gg c,\) la loi d'addition de vitesse de relativité spéciale se réduit à la loi de vitesse galiléenne. Lorsque la vitesse\(S'\) relative\(v\) de\(S\) est comparable à la vitesse de la lumière, la loi relativiste d'addition de vitesse donne un résultat bien inférieur à celui de l'addition de vitesse classique (galiléenne).
Supposons qu'un vaisseau spatial se dirigeant directement vers la Terre à la moitié de la vitesse de la lumière nous envoie un signal sur un faisceau de lumière produit par laser (Figure\(\PageIndex{2}\)). Étant donné que la lumière quitte le navire à la vitesse\(c\) observée depuis le navire, calculez la vitesse à laquelle elle s'approche de la Terre.
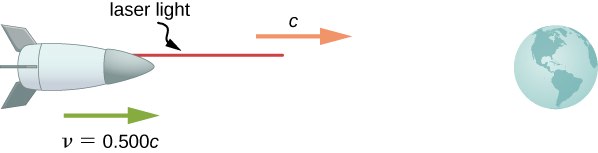
Stratégie
Comme la lumière et le vaisseau spatial se déplacent à des vitesses relativistes, nous ne pouvons pas utiliser la simple addition de vitesse. Nous déterminons plutôt la vitesse à laquelle la lumière s'approche de la Terre en utilisant l'addition de vitesse relativiste.
Solution
Identifiez les connus :\(v = 0.500c\) ;\(u' = c\).
Identifiez l'inconnu :\(u\).
Exprimez la réponse sous forme d'équation :\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
Effectuez le calcul :
\[ \begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + c}{1 + \dfrac{(0.500c) (c)}{c^2}} \\[4pt] &= \dfrac{(0.500 + 1)c}{\left(\dfrac{c^2 + 0.500c^2}{c^2}\right)} = c. \end{align*} \nonumber \]
L'importance
L'addition de vélocité relativiste donne le bon résultat. La lumière quitte le navire à toute allure\(c\) et s'approche de la Terre à toute allure\(c\). La vitesse de la lumière est indépendante du mouvement relatif de la source et de l'observateur, que l'observateur soit sur le navire ou sur la terre.
Les vitesses ne peuvent pas être supérieures à la vitesse de la lumière, à condition qu'elle\(v\) soit inférieure\(c\) et\(u'\) ne dépasse pas\(c\). L'exemple suivant montre que l'addition de vitesse relativiste n'est pas aussi symétrique que l'addition de vitesse classique.
Supposons que le vaisseau spatial de l'exemple précédent s'approche de la Terre à la moitié de la vitesse de la lumière et tire une cartouche à une vitesse de\(0.750c\) (Figure\(\PageIndex{3}\)).
- À quelle vitesse un observateur se dirigeant vers la Terre voit-il la cartouche si elle est projetée directement vers la Terre ?
- S'il est tiré directement loin de la Terre ?
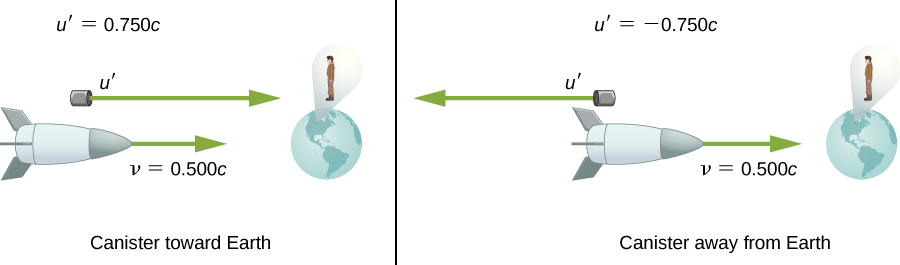
Stratégie
Comme la cartouche et le vaisseau spatial se déplacent à des vitesses relativistes, nous devons déterminer la vitesse de la cartouche par un observateur terrestre en utilisant l'addition de vitesse relativiste au lieu d'une simple addition de vitesse.
Solution pour (a)
- Identifiez les connus :\(v = 0.500c\) ;\(u' = 0.750c\).
- Identifiez l'inconnu :\(u\).
- Exprimez la réponse sous forme d'équation :\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
- Effectuez le calcul :\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + 0.750c}{1 + \dfrac{(0.500c)(0.750c)}{c^2}} \\[4pt] &= 0.909c. \end{align*} \nonumber \]
Solution pour (b)
- Identifiez les connus :\(v = 0.500c\) ;\(u' = - 0.750c\).
- Identifiez l'inconnu :\(u\).
- Exprimez la réponse sous forme d'équation :\(u = \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}}\).
- Effectuez le calcul :\[\begin{align*} u &= \dfrac{v + u'}{1 + \dfrac{vu'}{c^2}} \\[4pt] &= \dfrac{0.500c + (-0.750c)}{1 + \dfrac{(0.500c)(-0.750c)}{c^2}} \\[4pt] &=- 0.400c. \end{align*} \nonumber \]
L'importance
Le signe moins indique une vitesse s'éloignant de la Terre (dans la direction opposée à\(v\)), ce qui signifie que la cartouche se dirige vers la Terre dans la partie (a) et s'éloigne dans la partie (b), comme prévu. Mais les vitesses relativistes ne s'additionnent pas aussi simplement qu'elles le sont de façon classique. En partie (a), la cartouche s'approche de la Terre plus rapidement, mais à une vitesse inférieure à la somme vectorielle des vitesses, ce qui donnerait\(1.250c\). Dans la partie (b), la cartouche s'éloigne de la Terre à une vitesse de −0,400 °C, soit plus vite que la vitesse de −0,250 °C attendue classiquement. Les différences de vitesse ne sont même pas symétriques : dans la partie (a), un observateur sur Terre voit la cartouche et le navire s'éloigner à une vitesse de 0,409 c, et à une vitesse de 0,900 c dans la partie (b).
Les distances le long d'une direction perpendiculaire au mouvement relatif des deux images sont les mêmes dans les deux images. Pourquoi alors les vitesses perpendiculaires à la direction x sont-elles différentes dans les deux images ?
- Réponse
-
Bien que les déplacements perpendiculaires au mouvement relatif soient les mêmes dans les deux cadres de référence, l'intervalle de temps entre les événements diffère,\(dt\) et les différences et\(dt'\) conduisent à des vitesses différentes observées depuis les deux cadres.


