5.6 : La transformation de Lorentz
- Page ID
- 189731
- Décrire la transformation galiléenne de la mécanique classique, en reliant la position, le temps, les vitesses et les accélérations mesurées dans différents cadres inertiels
- Dérivez les équations de transformation de Lorentz correspondantes qui, contrairement à la transformation galiléenne, sont cohérentes avec la relativité spéciale
- Expliquer la transformation de Lorentz et de nombreuses caractéristiques de la relativité en termes d'espace-temps en quatre dimensions
Nous avons utilisé les postulats de la relativité pour examiner, dans des exemples particuliers, comment les observateurs de différents cadres de référence mesurent différentes valeurs pour les longueurs et les intervalles de temps. Nous pouvons mieux comprendre comment les postulats de la relativité modifient la vision newtonienne du temps et de l'espace en examinant les équations de transformation qui donnent les coordonnées spatiales et temporelles des événements d'un référentiel inertiel par rapport à ceux d'un autre. Nous examinons d'abord comment les coordonnées de position et de temps se transforment entre des trames inertielles selon le point de vue de la physique newtonienne. Nous examinons ensuite comment cela doit être modifié pour être en accord avec les postulats de la relativité. Enfin, nous examinons les équations de transformation de Lorentz qui en résultent et certaines de leurs conséquences en termes de diagrammes spatio-temporels en quatre dimensions, pour étayer l'idée que les conséquences de la relativité spéciale résultent des propriétés du temps et de l'espace eux-mêmes, plutôt que de l'électromagnétisme.
Les équations de transformation de Galilée
Un événement est spécifié par son emplacement et son heure\((x, y, z, t)\) par rapport à un référentiel inertiel particulier\(S\). Par exemple,\((x, y, z, t)\) cela pourrait indiquer la position d'une particule à la fois\(t\), et nous pourrions examiner ces positions à de nombreuses reprises afin de suivre le mouvement de la particule. Supposons qu'un second cadre de référence\(S'\) se déplace avec une certaine vélocité\(v\) par rapport au premier. Pour des raisons de simplicité, supposons que cette vitesse relative se situe le long de l'axe X. La relation entre le temps et les coordonnées dans les deux référentiels est alors
\[\begin{align} x &= x' + vt \label{eq1} \\[4pt] y &= y' \label{eq2} \\[4pt] x &= z'. \label{eq3} \end{align} \]
Ces équations supposent implicitement que les mesures de temps effectuées par les observateurs dans les deux\(S\) et\(S'\) sont les mêmes. C'est-à-dire,
\[t = t' \label{eq4} \]
Les équations \ ref {eq1} - \ ref {eq4} sont connues collectivement sous le nom de transformation galiléenne.
Nous pouvons obtenir les équations de transformation de vitesse et d'accélération galiléennes en différenciant ces équations par rapport au temps. Dans ce chapitre, nous utilisons\(u\) la vitesse d'une particule pour la distinguer de\(v\) la vitesse relative de deux repères. Notez que, pour la transformation galiléenne, l'incrément de temps utilisé pour différencier pour calculer la vitesse des particules est le même dans les deux images,\(dt = dt'\). Des rendements de différenciation
\[u_x = u'_x + v, \,u_y = u'_y, \,u_z = u'_z \nonumber \]
et
\[a_x = a'_x, \,a_y = a'_y, \,a_z = a'_z. \nonumber \]
Nous désignons la vitesse de la particule par\(u\) plutôt que\(v\) pour éviter toute confusion avec la vitesse\(v\) d'un référentiel par rapport à l'autre. Les vitesses de chaque image diffèrent de la vitesse d'une image vue de l'autre image. Les observateurs des deux cadres de référence mesurent la même valeur de l'accélération. Comme la masse reste inchangée par la transformation et que les distances entre les points ne sont pas chargées, les observateurs des deux images voient les mêmes forces\(F = ma\) agissant entre les objets et la même forme des deuxième et troisième lois de Newton dans toutes les images inertielles. Les lois de la mécanique sont conformes au premier postulat de la relativité.
Les équations de transformation de Lorentz
La transformation galiléenne viole néanmoins les postulats d'Einstein, car les équations de vitesse indiquent qu'une impulsion de lumière se déplaçant rapidement\(c\) le long de l'axe x se déplacerait rapidement\(c - v\) dans l'autre cadre inertiel. Plus précisément, l'impulsion sphérique a un rayon\(r = ct\) à la fois\(t\) dans la trame non amorcée, et a également un rayon\(r' = ct'\) à l'instant t'dans la trame amorcée. L'expression de ces relations en coordonnées cartésiennes donne
\[ \begin{align} x^2 + y^2 + z^2 - c^2t^2 &= 0 \label{eq21} \\[4pt] x'^2 + y'^2 + z'^2 - c^2t'^2 &= 0. \label{eq22} \end{align} \]
Les équations du côté gauche \ ref {eq21} et \ ref {eq22} peuvent être mises égales car les deux sont égales à zéro. Parce que\(y = y'\) et\(z = z'\), nous obtenons
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
Cela ne peut pas être satisfait pour une vitesse relative non nulle\(v\) des deux images si nous supposons que la transformation galiléenne aboutit\(t = t'\) à\(x = x' + vt'\).
Pour trouver le jeu correct d'équations de transformation, supposons les deux systèmes de coordonnées\(S\) et\(S'\) dans la Figure\(\PageIndex{1}\). Supposons d'abord qu'un événement se produise à\((x', 0, 0, t')\) in\(S'\) et à\((x, 0, 0, t)\) in\(S\), comme illustré dans la Figure\(\PageIndex{1}\).
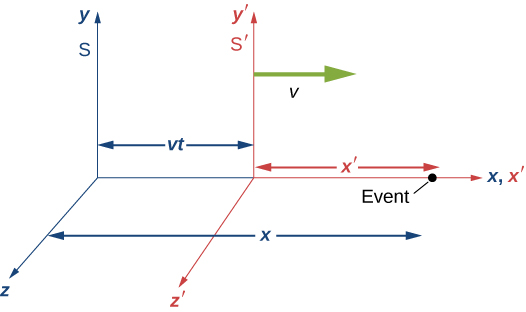
Supposons qu'au moment où les origines des systèmes de coordonnées de S et de S'coïncident, une ampoule flash émet une impulsion lumineuse à diffusion sphérique à partir de l'origine. À l'instant t, un observateur dans S trouve que l'origine de S'se trouve à\(x = vt\). Avec l'aide d'un ami en S, l'observateur S'mesure également la distance entre l'événement et l'origine de S'et trouve que c'est le cas\(x'\sqrt{1 - v^2/c^2}\). Cela s'explique par le fait que nous avons déjà montré que les postulats de la relativité impliquent une contraction de la longueur. Ainsi, la position de l'événement dans S est
\[x = vt + x'\sqrt{1 - v^2/c^2} \nonumber \]
et
\[x' = \dfrac{x - vt}{x'\sqrt{1 - v^2/c^2}}. \label{eq10} \]
Les postulats de la relativité impliquent que l'équation reliant la distance et le temps du front d'onde sphérique :
\[x^2 + y^2 + z^2 - c^2t^2 = 0 \nonumber \]
doit s'appliquer à la fois en termes de coordonnées amorcées et non amorcées, ce qui a été indiqué ci-dessus pour mener à l'équation :
\[x^2 - c^2t^2 = x'^2 - c^2t'^2. \nonumber \]
Nous combinons cela avec l'équation \ ref {eq10} qui se rapporte\(x\) et\(x′\) pour obtenir la relation entre\(t\) et\(t'\) :
\[t' = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
Les équations reliant le temps et la position des événements tels qu'ils sont vus dans\(S\) sont alors
\[ \begin{align} t &= \dfrac{t' + vx'/c^2}{\sqrt{1 - v^2/c^2}}. \\[4pt] x &= \dfrac{x' + vt'}{\sqrt{1 - v^2/c^2}}. \\[4pt] y &= y' \\[4pt] z &= z'. \end {align} \nonumber \]
Cet ensemble d'équations, reliant la position et le temps dans les deux cadres inertiels, est connu sous le nom de transformation de Lorentz. Ils sont nommés en l'honneur de H.A. Lorentz (1853-1928), qui les a proposés pour la première fois. Il est intéressant de noter qu'il a justifié la transformation sur une hypothèse qui s'est finalement révélée être une hypothèse fallacieuse. La base théorique correcte est la théorie spéciale de la relativité d'Einstein.
La transformation inverse exprime les variables\(S\) en termes de celles de S'. Le simple fait d'échanger les variables amorcées et non amorcées et de les substituer donne :
\[\begin{align*} t'& = \dfrac{t - vx/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] x' &= \dfrac{x - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] y' &= y \\[4pt] z' &= z. \end{align*} \nonumber \]
Le vaisseau S'est dirigé vers Alpha Centauri lorsque le vaisseau S le dépasse à une vitesse relative c /2. Le capitaine du S'envoie un signal radio qui dure 1,2 s selon l'horloge du navire. Utilisez la transformation de Lorentz pour déterminer l'intervalle de temps du signal mesuré par le responsable des communications du vaisseau spatial S.
Solution
- Identifiez les éléments connus :\(\Delta t' = t'_2 - t'_1 = 1.2 s; \,\Delta x' = x'_2 - x'_1 = 0.\)
- Identifiez l'inconnu :\(\Delta t = t_2 - t_1\).
- Exprimez la réponse sous forme d'équation. Le signal horaire commence par (\(x', t'_1\)) et s'arrête à (\(x', t'_1\)). Notez que la coordonnée x' des deux événements est la même car l'horloge est au repos en S'. Écrivez la première équation de transformation de Lorentz en termes de\(\Delta t = t_2 - t_1\)\(\Delta x = x_2 - x_1\), et de même pour les coordonnées amorcées, comme suit :
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
Parce que la position de l'horloge dans S'est fixe et que l'intervalle de temps\(\Delta t\) devient :\(\Delta x' = 0\)\[\Delta t = \dfrac{\Delta t'}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
- Fais le calcul.
\(\Delta t' = 1.2 \,s\)Cela donne :
\[\begin{align*} \Delta t &= \dfrac{1.2 \,s}{\sqrt{1 - \left(\dfrac{1}{2}\right)^2}} \\[4pt] &= 1.6 \,s. \end{align*} \nonumber \]
Notez que la transformation de Lorentz reproduit l'équation de dilatation dans le temps.
Un géomètre mesure la\(L = 100 \,m\) longueur d'une rue dans le cadre terrestre\(S\). Utilisez la transformation de Lorentz pour obtenir une expression de sa longueur mesurée à partir d'un vaisseau spatial\(S'\) se déplaçant à grande vitesse\(0.20c\), en supposant que les\(x\) coordonnées des deux images coïncident dans le temps\(t = 0\).
Solution
- Identifier les éléments connus :\(L = 100 \,m\) ;\(v = 0.20 c\) ;\(\Delta \tau = 0\).
- Identifiez l'inconnu :\(L'\).
- Exprimez la réponse sous forme d'équation. L'arpenteur du cadre S a mesuré les deux extrémités du bâton simultanément et les a trouvées au repos et à\(x_1\) une certaine\(L = x_2 - x_1 = 100 \,m\) distance l'\(x_2\)une de l'autre. L'équipage du vaisseau spatial mesure la position simultanée des extrémités des bâtons dans leur cadre. Pour relier les longueurs enregistrées par les observateurs dans S'et S, respectivement, écrivez la deuxième des quatre équations de transformation de Lorentz comme suit :
\[\begin{align*} x'_2 - x'_1 &= \dfrac{x_2 - vt}{\sqrt{1 - v^2/c^2}} - \dfrac{x_1 - vt}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{x_2 - x_2}{\sqrt{1 - v^2/c^2}} \\[4pt] &= \dfrac{L}{\sqrt{1 - v^2/c^2}}. \end{align*} \nonumber \]
- Fais le calcul. Parce\(x_2 - x_1 = 100 \,m\) que la longueur du bâton mobile est égale à :
\[\begin{align*} L' &= (100 \,m)\sqrt{1 - v^2/c^2} \\[4pt] &= (100 \,m)\sqrt{1 - (0.20)^2} = 98.0 \,m. \end{align*} \nonumber \]
Notez que la transformation de Lorentz a donné l'équation de contraction de la longueur pour la rue.
L'observateur représenté sur la figure\(\PageIndex{2}\) debout près de la voie ferrée voit les deux ampoules clignoter simultanément aux deux extrémités de la voiture particulière de 26 m de long lorsque le milieu de la voiture le dépasse à une vitesse de c /2. Trouvez l'intervalle dans le temps entre le moment où les ampoules clignotent, comme le voit le passager du train assis au milieu de la voiture.
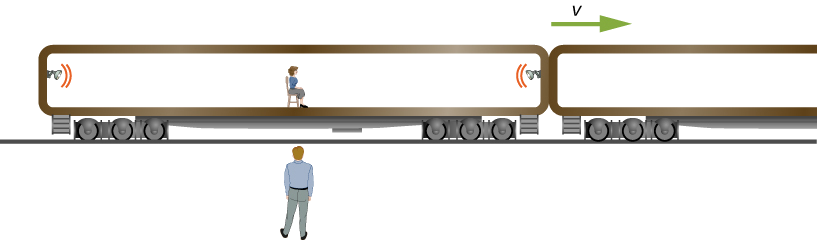
Solution
- Identifiez ce qui est connu :\(\Delta t = 0\).
Notez que la séparation spatiale des deux événements se situe entre les deux lampes, et non la distance entre la lampe et le passager.
- Identifiez l'inconnu :\(\Delta t' = t'_2 - t'_1.\).
Encore une fois, notez que l'intervalle de temps se situe entre les clignotements des lampes, et non entre les heures d'arrivée pour atteindre le passager.
- Exprimez la réponse sous forme d'équation :
\[\Delta t = \dfrac{\Delta t' + v\Delta x'/c^2}{\sqrt{1 - v^2/c^2}}. \nonumber \]
- Effectuez le calcul :
\[\begin{align*} 0 &= \dfrac{\Delta t' + \dfrac{c}{2} (26 \,m)/c^2}{\sqrt{1 - v^2/c^2}} \\[4pt] \Delta t' &= - \dfrac{26 \,m/s}{2c} = - \dfrac{26 \,m/s}{2(3.00 \times 10^8 \,m/s)} \\[4pt] &= -4.33 \times 10^{-8}\,s. \end{align*} \nonumber \]
L'importance
Le signe indique que l'événement le plus important,\(x'_2\) à savoir le flash provenant de la droite, est considéré comme se produisant en premier dans le cadre S'S', comme cela a été constaté précédemment pour cet exemple, de sorte que\(t_2 < t_1\).
Espace-Temps
Les phénomènes relativistes peuvent être analysés en termes d'événements dans un espace-temps quadridimensionnel. Lorsque des phénomènes tels que le double paradoxe, la dilatation du temps, la contraction de la longueur et la dépendance de la simultanéité au mouvement relatif sont considérés de cette manière, ils sont considérés comme caractéristiques de la nature de l'espace et du temps, plutôt que comme des aspects spécifiques de l'électromagnétisme.
Dans l'espace tridimensionnel, les positions sont spécifiées par trois coordonnées sur un ensemble d'axes cartésiens, et le déplacement d'un point par rapport à un autre est donné par :
\[(\Delta x, \,\Delta y, \,\Delta z) = (x_2 - x_1, \,y_2 - y-1, \,z_2 - z_1). \nonumber \]
La distance\(\Delta r\) entre les points est
\[\Delta r^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2. \nonumber \]
La distance\(\Delta r\) est invariante lors d'une rotation des axes. Si un nouvel ensemble d'axes cartésiens pivotés autour de l'origine par rapport aux axes d'origine est utilisé, chaque point de l'espace aura de nouvelles coordonnées en termes de nouveaux axes, mais la distance\(\Delta r'\) donnée par
\[\Delta r'^2 = (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2. \nonumber \]
Cela a la même valeur que celle que\(\Delta r^2\) j'avais. Quelque chose de similaire se produit avec la transformation de Lorentz dans l'espace-temps.
Définissez la séparation entre deux événements, chacun étant donné par un ensemble de x, y, z÷ et ct le long d'un système cartésien quadridimensionnel d'axes dans l'espace-temps, comme
\[(\Delta x, \,\Delta y, \,\Delta z, \,c\Delta t) = (x_2 - x_1, \,y_2 - y_1, \,z_2 - z_1, \,c(t_2 - t_1)). \nonumber \]
Définissez également l'intervalle spatio-temporel\(Δs\) entre les deux événements comme
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
Si les deux événements ont la même valeur de ct dans le référentiel considéré,\(\Delta s\) cela correspondrait à la distance\(\Delta r\) entre des points dans l'espace.
La trajectoire d'une particule dans l'espace-temps consiste en des événements (x, y, z÷ ct) qui indiquent un emplacement à chaque moment de son mouvement. Le trajet à travers l'espace-temps est appelé la ligne mondiale de la particule. La ligne mondiale d'une particule qui reste au repos au même endroit est une ligne droite parallèle à l'axe du temps. Si la particule se déplace à vitesse constante parallèlement à l'axe x, sa ligne mondiale serait une ligne inclinée\(x = vt\), correspondant à un simple graphique du déplacement en fonction du temps. Si la particule accélère, sa ligne mondiale est incurvée. L'incrément de s le long de la ligne mondiale de la particule est donné sous forme différentielle
\[ds^2 = (dx)^2 + (dy)^2 + (dz)^2 - c^2(dt)^2. \nonumber \]
Tout comme la distance\(\Delta r\) est invariante lors de la rotation des axes spatiaux, l'intervalle spatio-temporel :
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
est invariant sous la transformation de Lorentz. Cela découle des postulats de la relativité et peut également être vu par la substitution des équations de transformation de Lorentz précédentes par l'expression de l'intervalle spatio-temporel :
\[\begin{align*} \Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \\[4pt] &=\left(\dfrac{\Delta x' + v\Delta t'}{\sqrt{1 - v^2/c^2}}\right)^2 + (\Delta y')^2 + (\Delta z')^2 - \left(c\dfrac{\Delta t' + \dfrac{v\Delta x'}{c^2}}{\sqrt{1 - v^2/c^2}}\right)^2 \nonumber \]\[= (\Delta x')^2 + (\Delta y')^2 + (\Delta z')^2 - (c\Delta t')^2 \\[4pt] &= \Delta s'^2. \end{align*} \nonumber \]
De plus, la transformation de Lorentz modifie les coordonnées d'un événement dans le temps et dans l'espace de la même manière qu'une rotation tridimensionnelle transforme les anciennes coordonnées en nouvelles coordonnées :
|
Transformation de Lorentz (coordonnées x, t) : |
Axe : rotation autour de z - un axe (coordonnées x, t) : |
|---|---|
|
\(x' = (γ)x + (−βγ)ct\) |
\(x' = (\cos θ)x + (\sin θ)y\) |
| \(ct' = (−βγ)x + (γ)ct\) | \(y' = (−\sin θ)x + (\cos θ)y\) |
où\(\gamma = \dfrac{1}{\sqrt{1 - \beta^2}}\) ;\(\beta = v/c\).
Les transformations de Lorentz peuvent être considérées comme des généralisations des rotations spatiales à l'espace-temps. Cependant, il existe certaines différences entre la rotation d'un axe tridimensionnel et une transformation de Lorentz impliquant l'axe du temps, en raison des différences dans la façon dont la métrique, ou la règle de mesure\(\Delta r\) des déplacements\(\Delta s\), diffère. Bien qu'elle\(\Delta r\) soit invariante lors de rotations spatiales et qu'elle\(\Delta s\) soit invariante également sous la transformation de Lorentz, la transformation de Lorentz impliquant l'axe du temps ne conserve pas certaines caractéristiques, telles que les axes restant perpendiculaires ou l'échelle de longueur le long de chaque axe restant la même.
Notez que la quantité\(\Delta s^2\) peut avoir l'un ou l'autre signe, en fonction des coordonnées des événements spatio-temporels impliqués. Pour les paires d'événements qui lui donnent un signe négatif, il est utile de le définir\(c^2 \Delta \tau^2\) comme\(-\Delta s^2\). La signification de\(c^2 \Delta \tau\) ce qui vient d'être défini suit en notant que, dans un cadre de référence où les deux événements se produisent au même endroit, nous avons\(\Delta x = \Delta y = \Delta z = 0\) et donc (à partir de l'équation pour\(\Delta s^2 = - c^2 \Delta \tau^2\)) :
\[c^2 \Delta \tau^2 = - \Delta s^2 = (c^2 \Delta t)^2. \nonumber \]
Il\(c^2 \Delta \tau\) s'agit donc de l'intervalle de temps\(c^2 \Delta t\) dans le cadre de référence où les deux événements se produisent au même endroit. Il s'agit du même intervalle de temps approprié dont il a été question plus haut. Il découle également de la relation entre\(\Delta s\) et\(c^2 \Delta \tau\) que, comme Lorentz\(\Delta s\) est invariant, le temps approprié est également invariant de Lorentz. Tous les observateurs, quel que soit le cadre inertiel, s'accordent sur les intervalles de temps appropriés entre les deux mêmes événements.
Montrez que si un incrément de temps s'\(dt\)écoule pour un observateur qui voit la particule se déplacer avec vélocité\(v\), cela correspond à un incrément temporel approprié pour la particule de\(d\tau = \gamma dt\).
- Réponse
-
Commencez par définir l'incrément de temps approprié :
\[d\tau = \sqrt{-(ds)^2 /c^2} = \sqrt{dt^2 - (dx^2 + dx^2 + dx^2)/c^2}. \nonumber \]
où\((dx, dy, dx, cdt)\) sont mesurés dans la base inertielle d'un observateur qui ne voit pas nécessairement cette particule au repos. Cela devient donc
\[d\tau = \sqrt{-(ds)^2/c^2} = \sqrt{dt^2 - [(dx)^2 + (dy)^2 + (dz)^2]/c^2} \nonumber \]
\[dt\sqrt{1 - \left[ \left(\dfrac{dx}{dt}\right)^2 + \left(\dfrac{dy}{dt}\right)^2 + \left(\dfrac{dz}{dt}\right)^2\right] /c^2} \nonumber \]\[dt\sqrt{1 - v^2/c^2} \nonumber \]\[dt = \gamma d\tau. \nonumber \]
Le cône de lumière
Nous pouvons surmonter la difficulté de visualiser et d'esquisser des graphes en quatre dimensions en imaginant les trois coordonnées spatiales devant être représentées collectivement par un axe horizontal, et l'axe vertical comme étant l'axe ct. En commençant par un événement particulier de l'espace-temps comme origine du graphe spatio-temporel illustré, la ligne mondiale d'une particule qui reste au repos à l'emplacement initial de l'événement à l'origine est alors l'axe du temps. Tout plan passant par l'axe temporel parallèle aux axes spatiaux contient tous les événements qui sont simultanés entre eux et à l'intersection du plan et de l'axe temporel, comme le montre le cadre de repos de l'événement à l'origine.
Il est utile de représenter un cône lumineux sur le graphique, formé par les lignes mondiales de tous les faisceaux lumineux passant par l'événement d'origine A, comme le montre la figure\(\PageIndex{3}\). Le cône de lumière, selon les postulats de la relativité, a des côtés formant un angle de 45° si l'axe du temps est mesuré en unités de ct et, selon les postulats de la relativité, le cône de lumière reste le même dans toutes les images inertielles. Comme l'événement A est arbitraire, chaque point du diagramme spatio-temporel est associé à un cône lumineux.
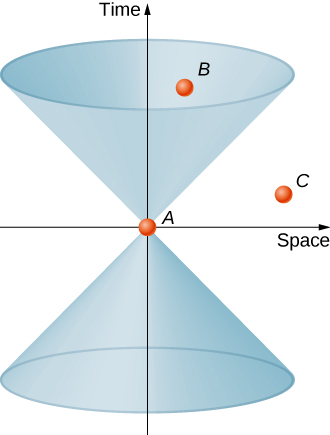
Considérons maintenant la ligne mondiale d'une particule dans l'espace-temps. Toute ligne mondiale située à l'extérieur du cône, telle qu'une ligne passant de A à C, impliquerait des vitesses supérieures à c et ne serait donc pas possible. Les événements tels que C qui se situent à l'extérieur du cône lumineux sont considérés comme séparés de l'événement A. Ils se caractérisent par :
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - y_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
Un événement tel que B qui se trouve dans le cône supérieur est accessible sans dépasser la vitesse de la lumière dans le vide et se caractérise par
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
On dit que l'événement a une séparation temporelle avec A. Les événements temporels qui tombent dans la moitié supérieure du cône lumineux se produisent à des valeurs t supérieures à l'heure de l'événement A au sommet et se produisent dans le futur par rapport à A. Les événements qui se séparent de A dans le temps et qui tombent dans la moitié inférieure du cône lumineux appartiennent au passé et peuvent affecter l'événement à l'origine. La région située à l'extérieur du cône de lumière n'est étiquetée ni comme passée ni future, mais plutôt comme « ailleurs ».
Pour tout événement présentant une séparation spatiale par rapport à l'événement d'origine, il est possible de choisir un axe temporel qui fera en sorte que les deux événements se produisent en même temps, de sorte que les deux événements soient simultanés dans un cadre de référence. Par conséquent, lequel des événements présentant une séparation semblable à l'espace précède l'autre dans le temps dépend également du cadre de référence de l'observateur. Comme les séparations semblables à celles de l'espace ne peuvent être traversées qu'en dépassant la vitesse de la lumière, cette violation de l'événement qui peut provoquer l'autre fournit un autre argument expliquant pourquoi les particules ne peuvent pas se déplacer plus vite que la vitesse de la lumière, ainsi que du matériel potentiel pour la science-fiction sur le voyage dans le temps. De même, pour tout événement présentant une séparation temporelle de l'événement à l'origine, il est possible de trouver un cadre de référence qui fera en sorte que les événements se produisent au même endroit. Parce que les relations
\[\Delta s_{AC}^2 = (x_A - x_C)^2 + (y_A - x_C)^2 + (z_A - z_C)^2 - (c\Delta t)^2 > 0. \nonumber \]
et
\[\Delta s_{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 + (z_A - z_B)^2 - (c\Delta t)^2 <0. \nonumber \]
sont invariants de Lorentz, que deux événements soient temporels et puissent se produire au même endroit ou dans l'espace et qu'ils puissent se produire en même temps est identique pour tous les observateurs. Tous les observateurs de différents référentiels inertiels s'accordent sur la question de savoir si deux événements ont une séparation temporelle ou spatiale.
Le double paradoxe vu dans l'espace-temps
Le double paradoxe évoqué précédemment implique un jumeau astronaute se déplaçant à une vitesse proche de la lumière vers un système stellaire lointain et retournant sur Terre. En raison de la dilatation du temps, on prévoit que le jumeau spatial vieillira beaucoup moins que le jumeau terrestre. Cela semble paradoxal, car nous aurions pu nous attendre à première vue à ce que le mouvement relatif soit symétrique et avons naïvement pensé qu'il était également possible de soutenir que le jumeau lié à la terre devrait vieillir moins longtemps.
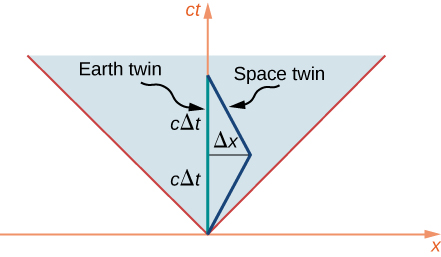
Pour analyser cela en termes de diagramme spatio-temporel, supposons que l'origine des axes utilisés est fixe sur Terre. La ligne mondiale du jumeau terrestre se trouve alors le long de l'axe du temps.
La ligne mondiale du jumeau astronaute, qui se déplace vers l'étoile lointaine puis revient, doit s'écarter d'une trajectoire en ligne droite afin de permettre un aller-retour. Comme le montre la figure\(\PageIndex{4}\), les circonstances des deux jumeaux ne sont pas du tout symétriques. Leurs parcours dans l'espace-temps sont d'une longueur manifestement différente. Plus précisément, la ligne mondiale du jumeau terrestre a une longueur\(2c\Delta t\), ce qui donne alors le temps approprié qui s'écoule pour le jumeau terrestre comme\(2\Delta t\). La distance jusqu'au système stellaire lointain est de\(\Delta x = v\Delta t\). Le temps qui s'écoule pour le jumeau spatial est celui\(2\Delta \tau\) où
\[c^2\Delta \tau^2 = - \Delta s^2 = (c\Delta t)^2 - (\Delta x)^2. \nonumber \]
C'est beaucoup plus court que le temps approprié pour le jumeau lié à la terre, selon le ratio
\[\dfrac{c\Delta \tau}{c\Delta t} = \sqrt{\dfrac{(c\Delta t)^2 - (\Delta x)^2}{(c\Delta t)^2}} = \sqrt{\dfrac{(c\Delta t)^2 - (v\Delta t)^2}{(c\Delta t)^2}} = \sqrt{1 - \dfrac{v^2}{c^2}} = \dfrac{1}{\gamma}. \nonumber \]
conforme à la formule de dilatation temporelle. Le double paradoxe est donc considéré comme n'étant pas du tout paradoxe. La situation des deux jumeaux n'est pas symétrique sur le diagramme spatio-temporel. La seule surprise est peut-être que le chemin apparemment plus long sur le diagramme spatio-temporel correspond au plus petit intervalle de temps approprié, en raison de comment\(\Delta \tau\) et\(\Delta s\) dépend de\(\Delta x\) et\(\Delta t\).
Les transformations de Lorentz dans l'espace-temps
Nous avons déjà noté comment la transformation de Lorentz part
\[\Delta s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\Delta t)^2. \nonumber \]
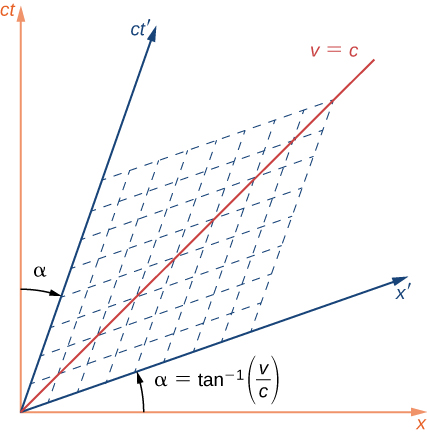
inchangé et correspond à une rotation des axes dans l'espace-temps quadridimensionnel. Si les trames S et S'sont en mouvement relatif le long de leur direction x commune, les axes spatial et temporel de S'sont pivotés d'un angle αα vu depuis S, de la manière illustrée sur la figure\(\PageIndex{5}\), où :
\[tan \,\alpha = \dfrac{v}{c} = \beta. \nonumber \]
Cela diffère d'une rotation dans le sens tridimensionnel habituel, dans la mesure où les deux axes spatio-temporels tournent l'un vers l'autre symétriquement en ciseaux, comme illustré. La rotation des axes temporel et spatial se fait selon le même angle. Le maillage de lignes pointillées parallèles aux deux axes indique comment les coordonnées d'un événement seraient lues le long des axes amorcés. Cela se ferait en suivant une ligne parallèle à l'axe x' et une parallèle à l'axe t', comme indiqué par les lignes pointillées. L'échelle de longueur des deux axes est modifiée comme suit :
\[ct' = ct\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}; \,x' = x\sqrt{\dfrac{1 + \beta^2}{1 - \beta^2}}. \nonumber \]
La droite étiquetée « v = c » à 45° par rapport à l'axe x correspond au bord du cône de lumière et n'est pas affectée par la transformation de Lorentz, conformément au deuxième postulat de la relativité. La ligne « v = c » et le cône lumineux qu'elle représente sont les mêmes pour les repères S et S'.
Simultanéité
La simultanéité des événements à des endroits séparés dépend du cadre de référence utilisé pour les décrire, tel que donné par la « rotation » en forme de ciseaux vers de nouvelles coordonnées temporelles et spatiales telles que décrites. Si deux événements ont les mêmes\(t\) valeurs dans le cadre de référence non amorcé, il n'est pas nécessaire qu'ils aient les mêmes valeurs mesurées le long de\(ct'\) l'axe et ne seraient donc pas simultanés dans le cadre amorcé.
Prenons l'exemple d'un train à vitesse proche de la lumière dans lequel les feux clignotants situés aux deux extrémités de la voiture clignotent simultanément dans le cadre de référence d'un observateur au sol. Le graphique spatio-temporel est illustré à la figure\(\PageIndex{6}\). Les éclairs des deux lampes sont représentés par les points étiquetés « Lampe flash gauche » et « Lampe flash droite » qui se trouvaient autrefois sur le cône lumineux. La ligne mondiale des deux impulsions se déplace le long du bord du cône lumineux pour atteindre simultanément l'observateur au sol. Leur arrivée est l'événement à l'origine. Ils ont donc dû être émis simultanément dans le cadre non amorcé, comme représenté par le point marqué comme\(t\) (les deux). Mais le temps est mesuré le long de l'axe ct dans le cadre de référence de l'observateur assis au milieu du wagon. Ainsi, dans son cadre de référence, l'événement d'émission des ampoules étiquetées\(t'\) (à gauche) et\(t'\) (à droite) n'était pas simultané.
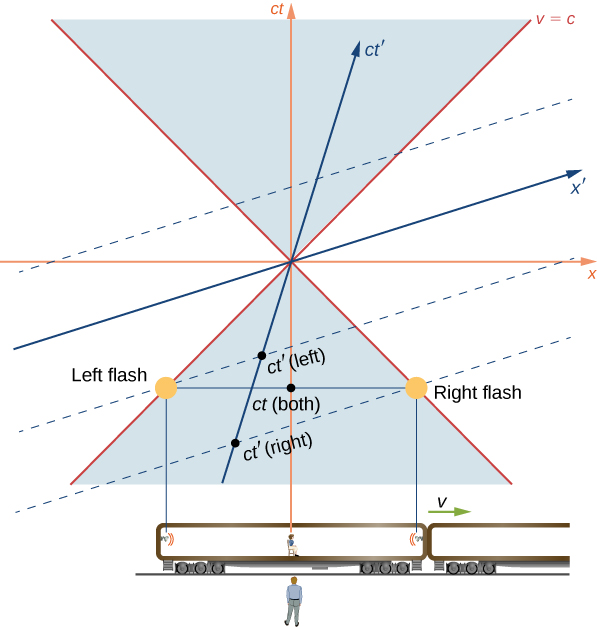
En termes de diagramme spatio-temporel, les deux observateurs utilisent simplement des axes temporels différents pour les mêmes événements parce qu'ils se trouvent dans des cadres inertiels différents, et les conclusions des deux observateurs sont également valables. Comme le suggère également l'analyse en termes de diagrammes spatio-temporels, la propriété selon laquelle la simultanéité des événements dépend du cadre de référence résulte des propriétés de l'espace et du temps eux-mêmes, plutôt que de tout ce qui concerne spécifiquement l'électromagnétisme.


