5.5 : Contraction de longueur
- Page ID
- 189687
À la fin de cette section, vous serez en mesure de :
- Expliquez comment la simultanéité et la contraction de la longueur sont liées.
- Décrivez la relation entre la contraction de la longueur et la dilatation temporelle et utilisez-la pour dériver l'équation longueur-contraction.
La longueur du wagon de la figure\(\PageIndex{1}\) est la même pour tous les passagers. Tous se mettraient d'accord sur l'emplacement simultané des deux extrémités de la voiture et obtiendraient le même résultat pour la distance qui les sépare. Mais les événements simultanés dans une trame inertielle ne doivent pas nécessairement être simultanés dans une autre. Si le train pouvait se déplacer à des vitesses relativistes, un observateur au sol verrait les positions simultanées des deux extrémités du wagon à une distance différente de celle des observateurs à l'intérieur du wagon. Les distances mesurées ne doivent pas nécessairement être les mêmes pour différents observateurs lorsque des vitesses relativistes sont impliquées.

Longueur appropriée
Deux observateurs qui se croisent voient toujours la même valeur de leur vitesse relative. Même si la dilatation du temps implique que le passager du train et l'observateur qui se tient le long des voies ferrées mesurent des temps différents pour le passage du train, ils s'accordent toujours à dire que la vitesse relative, qui est la distance divisée par le temps écoulé, est la même. Si un observateur au sol et un observateur dans le train mesurent un temps différent pour que le train passe devant l'observateur au sol, s'entendre sur leur vitesse relative signifie qu'ils doivent également voir les différentes distances parcourues.
Le muon discuté précédemment illustre ce concept (Figure\(\PageIndex{2}\)). Pour un observateur sur Terre, le muon se déplace à 0,950 °C pendant 7,05 μs entre le moment où il est produit et le moment où il se désintègre. Il parcourt donc une distance par rapport à la Terre de :
\[ \begin{align*} L_0 &= v\Delta t \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(7.05 \times 10^{-6}s) \\[4pt] &= 2.01 \, km. \end{align*} \nonumber \]
Dans la trame muonique, la durée de vie du muon est de 2,20 μs. Dans ce cadre de référence, la Terre, l'air et le sol n'ont que le temps nécessaire pour se déplacer :
\[ \begin{align*} L &= v\Delta r \\[4pt] &= (0.950)(3.00 \times 10^8 \, m/s)(2.20 \times 10^{-6}s) \\[4pt] &= 0.627 \, km. \end{align*} \nonumber \]
La distance entre les deux mêmes événements (production et désintégration d'un muon) dépend de la personne qui le mesure et de la façon dont il se déplace par rapport à celui-ci.
La longueur correcte\(L_0\) est la distance entre deux points mesurée par un observateur qui est au repos par rapport aux deux points.
L'observateur terrestre mesure la bonne longueur\(L_0\) parce que les points de production et de désintégration du muon sont stationnaires par rapport à la Terre. Par rapport au muon, la Terre, l'air et les nuages se déplacent, de sorte que la distance L qu'il voit n'est pas la bonne longueur.
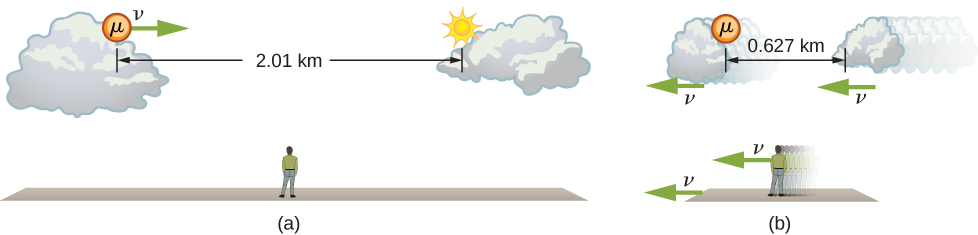
Longueur : Contraction
Pour relier les distances mesurées par différents observateurs, notez que la vitesse relative à l'observateur terrestre dans notre exemple de muons est donnée par
\[v = \dfrac{L_0}{\Delta t}. \nonumber \]
Le temps relatif à l'observateur terrestre est\(Δt\), car l'objet chronométré se déplace par rapport à cet observateur. La vitesse par rapport à l'observateur en mouvement est donnée par
\[v = \dfrac{L}{\Delta \tau}. \nonumber \]
L'observateur en mouvement voyage avec le muon et observe donc le bon moment\(\Delta \tau\). Les deux vitesses sont identiques ; ainsi,
\[\dfrac{L_0}{\Delta t} = \dfrac{L}{\Delta \tau}. \label{eq10} \]
Nous le savons\(\Delta t = \gamma \Delta \tau\) et la remplacer dans l'équation \ ref {eq10} donne
\[L = \dfrac{L_0}{\gamma}. \nonumber \]
La substitution de\(γ\) donne une équation reliant les distances mesurées par différents observateurs.
La contraction de la longueur est la diminution de la longueur mesurée d'un objet par rapport à sa longueur appropriée lorsqu'elle est mesurée dans un repère qui se déplace par rapport à l'objet :
\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} \label{contraction} \]
où\(L_0\) est la longueur de l'objet dans son cadre de repos et\(L\) la longueur du cadre se déplaçant avec la vitesse\(v\).
Si nous mesurons la longueur d'un objet qui bouge par rapport à notre cadre, nous constatons que sa longueur L est inférieure à la longueur correcte\(L_0\) qui serait mesurée si l'objet était immobile. Par exemple, dans le cadre de repos du muon, la distance parcourue par la Terre entre l'endroit où le muon a été produit et l'endroit où il s'est désintégré est plus courte que la distance parcourue depuis le cadre terrestre. Ces points sont fixes par rapport à la Terre mais se déplacent par rapport au muon. Les nuages et autres objets se contractent également dans la direction du mouvement, vus depuis le cadre de repos du muon.
Ainsi, deux observateurs mesurent des distances différentes le long de leur direction de mouvement relatif, en fonction de celui qui mesure les distances entre les objets au repos.
Mais qu'en est-il des distances mesurées dans une direction perpendiculaire au mouvement relatif ? Imaginez deux observateurs se déplaçant le long de leurs axes X et se croisant tout en tenant des bâtons de mesure verticalement dans la direction y. La figure\(\PageIndex{3}\) montre deux bâtons de mesure M et M'qui sont au repos dans les repères de référence de deux garçons S et S', respectivement. Un petit pinceau est fixé au sommet (la marque des 100 cm) du bâton M'. Supposons que S'se déplace vers la droite à une vitesse v très élevée par rapport à S, et que les baguettes soient orientées de telle sorte qu'elles soient perpendiculaires, ou transversales, à leur vecteur de vitesse relative. Les bâtonnets sont maintenus de telle sorte qu'au fur et à mesure qu'ils se croisent, leurs extrémités inférieures (les marques de 0 cm) coïncident. Supposons que lorsque S regarde ensuite son bâton M, il trouve une ligne peinte dessus, juste en dessous du haut du bâton. Comme la brosse est fixée au sommet du bâton M'de l'autre garçon, S ne peut que conclure que le bâton M'mesure moins de 1 m de long.
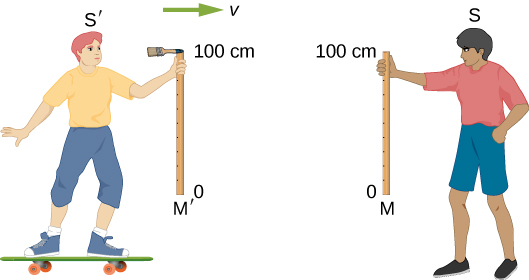
Maintenant, quand les garçons s'approchent l'un de l'autre, S', comme S, voit un mètre se déplacer vers lui avec la vitesse v. Comme leurs situations sont symétriques, chaque garçon doit prendre la même mesure du bâton dans l'autre cadre. Ainsi, si S mesure un bâton M'de moins de 1 m de long, S'doit mesurer un bâton M de moins de 1 m de long, et S'doit voir son pinceau passer par-dessus le dessus du bâton M sans tracer de ligne dessus. En d'autres termes, après le même événement, un garçon voit une ligne peinte sur un bâton, tandis que l'autre ne voit pas une telle ligne sur ce même bâton !
Le premier postulat d'Einstein exige que les lois de la physique (appliquées, par exemple, à la peinture) prédisent que S et S', qui se trouvent tous deux dans des cadres inertiels, font les mêmes observations ; c'est-à-dire que S et S'doivent soit voir une ligne peinte sur le bâton M, soit ne pas voir cette ligne. Nous sommes donc contraints de conclure que notre hypothèse initiale selon laquelle S avait vu une ligne peinte sous le haut de son bâton était erronée ! Au lieu de cela, S trouve la ligne peinte juste à la marque des 100 cm sur M. Ensuite, les deux garçons conviendront qu'une ligne est peinte sur M, et ils conviendront également que les deux bâtons mesurent exactement 1 m de long. Nous concluons donc que les mesures d'une longueur transversale doivent être les mêmes dans différents cadres inertiels.
Supposons qu'un astronaute, comme le jumeau dans la discussion sur le double paradoxe, voyage si vite que\(\gamma = 30.00\). a) L'astronaute voyage de la Terre vers le système stellaire le plus proche, Alpha Centauri, à 4 300 années-lumière (ly) de distance, tel que mesuré par un observateur terrestre. Quelle est la distance entre la Terre et Alpha Centauri telle que mesurée par l'astronaute ? (b) En termes de c, quelle est la vitesse de l'astronaute par rapport à la Terre ? Vous pouvez négliger le mouvement de la Terre par rapport au soleil (Figure\(\PageIndex{4}\)).
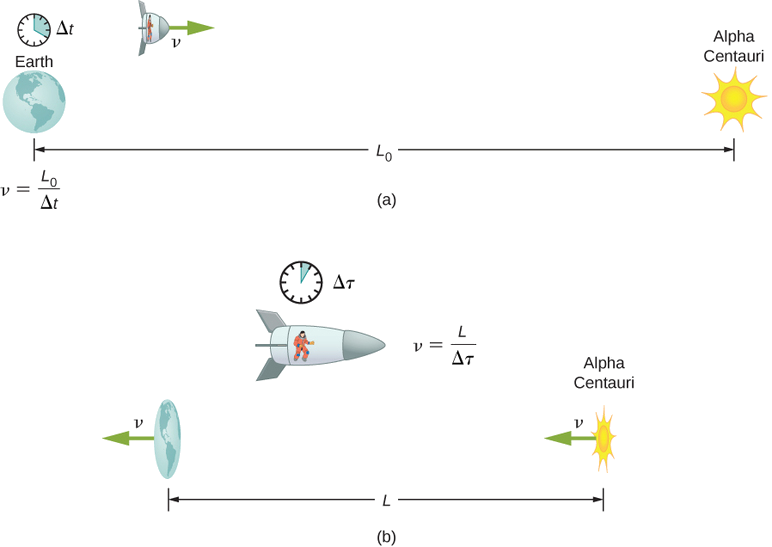
Stratégie
Tout d'abord, notez qu'une année-lumière (ly) est une unité de distance pratique à l'échelle astronomique, c'est-à-dire la distance parcourue par la lumière au cours d'une année. Pour la partie (a), la distance de 4 300 ly entre Alpha Centauri et la Terre est la bonne distance\(L_0\), car elle est mesurée par un observateur terrestre par rapport auquel les deux étoiles sont (approximativement) fixes. Pour l'astronaute, la Terre et Alpha Centauri se déplacent à la même vitesse, de sorte que la distance qui les sépare est la longueur contractée L. Dans la partie (b), nous sommes donnés\(\gamma\), afin que nous puissions trouver\(v\) en réorganisant la définition de\(\gamma\) pour exprimer\(v\) en termes de\(c\).
Solution pour (a)
Pour la partie (a) :
- Identifier les éléments connus :\(L_0 = 4.300 \, ly\)\(\gamma = 30.00.\)
- Identifiez l'inconnu : L.
- Exprimez la réponse sous forme d'équation :\(L = \dfrac{L_0}{\gamma}\).
- Effectuez le calcul :
\[\begin{align*} L &= \dfrac{L_0}{\gamma} \\[4pt] &= \dfrac{4.300 \, ly}{30.00} \\[4pt] &= 0.1433 \, ly. \end{align*} \nonumber \]
Solution pour (b)
Pour la partie (b) :
- Identifiez ce qui est connu :\(\gamma = 30.00\).
- Identifiez l'inconnu : v en termes de c.
- Exprimez la réponse sous forme d'équation. Commencez par :
\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]
Résolvez ensuite le v/c inconnu en mettant d'abord au carré les deux côtés, puis en réorganisant :\[\begin{align*} \gamma^2 &= \dfrac{1}{1 - \dfrac{v^2}{c^2}} \\[4pt] \dfrac{v^2}{c^2} &= 1 - \dfrac{1}{\gamma^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}}. \end{align*} \nonumber \]
- Effectuez le calcul :
\[\begin{align*} \dfrac{v}{c} &= \sqrt{1 - \dfrac{1}{\gamma^2}} \\[4pt] &= \sqrt{1 - \dfrac{1}{(30.00)^2}} \\[4pt] &= 0.99944\end{align*} \nonumber \]
ou\[v = 0.9994 \, c. \nonumber \]
Importance : N'oubliez pas de ne pas arrondir les calculs avant la réponse finale, sinon vous pourriez obtenir des résultats erronés. Cela est particulièrement vrai pour les calculs de relativité spéciale, où les différences peuvent n'être révélées qu'après plusieurs décimales. L'effet relativiste est important ici (\(\gamma = 30.00\)), et nous voyons que v s'approche (et n'est pas égal) de la vitesse de la lumière. Comme la distance mesurée par l'astronaute est beaucoup plus petite, l'astronaute peut la parcourir en beaucoup moins de temps dans son cadre.
Les personnes voyageant à des vitesses extrêmement élevées peuvent parcourir de très grandes distances (des milliers, voire des millions d'années-lumière) et ne vieillir que quelques années en cours de route. Cependant, comme les émigrants des siècles passés qui ont quitté leur foyer, ces personnes quitteraient la Terre qu'elles connaissent pour toujours. Même s'ils étaient revenus, des milliers, voire des millions d'années se seraient écoulées sur Terre, anéantissant la majeure partie de ce qui existe aujourd'hui. Il existe également un obstacle pratique plus sérieux à se déplacer à de telles vitesses ; des énergies beaucoup plus importantes seraient nécessaires pour atteindre des vitesses aussi élevées que ce que la physique classique prédit. Ce point sera abordé plus loin dans le chapitre.
Pourquoi ne remarquons-nous pas de contraction de longueur dans la vie de tous les jours ? La distance jusqu'à l'épicerie ne semble pas dépendre du fait que nous déménageons ou non. En examinant l'équation \ ref {contraction}, nous voyons qu'à de faibles vitesses (\(v \ll c\)), les longueurs sont presque égales, ce qui est une attente classique. Cependant, la contraction de la longueur est réelle, si elle n'est pas courante. Par exemple, une particule chargée telle qu'un électron se déplaçant à une vitesse relativiste possède des lignes de champ électrique qui sont comprimées le long de la direction du mouvement telle que vue par un observateur stationnaire (Figure\(\PageIndex{5}\)). Lorsque l'électron passe devant un détecteur, tel qu'une bobine de fil, son champ interagit beaucoup plus brièvement, un effet observé sur des accélérateurs de particules tels que l'accélérateur linéaire Stanford (SLAC) de 3 km de long. En fait, lorsqu'un électron se déplace dans le tube de faisceau du SLAC, l'accélérateur et la Terre se déplacent tous et se contractent en longueur. L'effet relativiste est si important que l'accélérateur ne mesure que 0,5 m de long par rapport à l'électron. Il est en fait plus facile de faire descendre le faisceau d'électrons dans le tuyau, car il n'est pas nécessaire que le faisceau soit orienté aussi précisément pour descendre dans un tuyau court que pour descendre un tuyau de 3 km de long. Il s'agit là encore d'une vérification expérimentale de la théorie spéciale de la relativité.
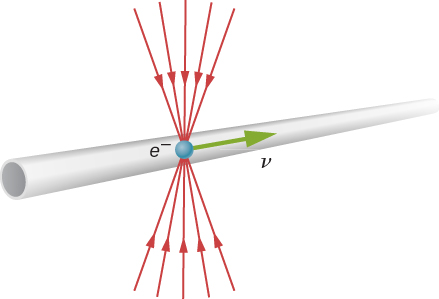
Une particule se déplace dans l'atmosphère terrestre à une vitesse de\(0.750c\). Pour un observateur terrestre, la distance parcourue est de 2,50 km. Quelle est la distance parcourue par la particule depuis son repère de référence ?
- Réponse
-
\[L = L_0\sqrt{1 - \dfrac{v^2}{c^2}} = (2.50 \, km)\sqrt{1 - \dfrac{(0.750c)^2}{c^2}} = 1.65 \, km \nonumber \]


