5.4 : Dilatation temporelle

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Expliquer comment les intervalles de temps peuvent être mesurés différemment dans différents cadres de référence.
• Décrivez comment distinguer un intervalle de temps approprié d'un intervalle de temps dilaté.
• Décrivez l'importance de l'expérience sur les muons.
• Expliquez pourquoi le double paradoxe n'est pas une contradiction.
• Calculez la dilatation temporelle en fonction de la vitesse d'un objet dans une image donnée.

L'analyse de la simultanéité montre que les postulats d'Einstein impliquent un effet important : les intervalles de temps ont des valeurs différentes lorsqu'ils sont mesurés dans différents cadres inertiels. Supposons, par exemple, qu'un astronaute mesure le temps nécessaire à une impulsion lumineuse pour parcourir une distance perpendiculaire à la direction du mouvement de son vaisseau (par rapport à un observateur terrestre), rebondir sur un miroir et revenir (Figure\(\PageIndex{1a}\)). Comment le temps écoulé que l'astronaute mesure dans l'engin spatial se compare-t-il au temps écoulé qu'un observateur terrestre mesure en observant ce qui se passe dans l'engin spatial ?

L'examen de cette question aboutit à un résultat profond. Le temps écoulé pour un processus dépend de l'observateur qui le mesure. Dans ce cas, le temps mesuré par l'astronaute (dans le vaisseau spatial où il est au repos) est inférieur au temps mesuré par l'observateur terrestre (vers lequel l'astronaute se déplace). Le temps écoulé pour le même processus est différent pour les observateurs, car la distance parcourue par l'impulsion lumineuse dans le cadre de l'astronaute est plus petite que dans le cadre terrestre, comme le montre la figure\(\PageIndex{1b}\). La lumière se déplace à la même vitesse dans chaque image, de sorte qu'il faut plus de temps pour parcourir la plus grande distance dans le cadre terrestre.

Figure\(\PageIndex{1}\) : (a) Un astronaute mesure le temps nécessaire à la lumière\(\Delta \tau\) pour parcourir une distance en 2D dans le cadre de l'astronaute. (b) Un scientifique de la NASA sur Terre voit la lumière suivre le plus long trajet 2 s et prendre plus de temps\(\Delta t\). (c) Ces triangles sont utilisés pour trouver la relation entre les deux distances D et s.

Définition : Dilatation temporelle

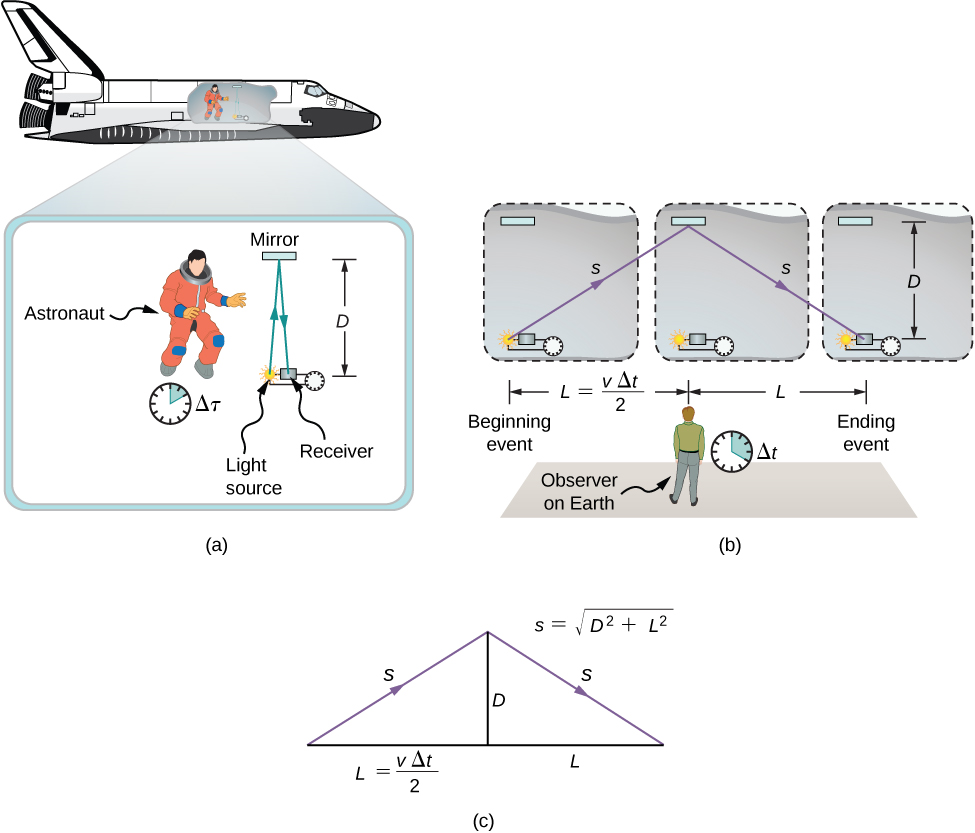
La dilatation temporelle est l'allongement de l'intervalle de temps entre deux événements pour un observateur dans une trame inertielle qui se déplace par rapport à la trame restante des événements (dans laquelle les événements se produisent au même endroit).

Pour comparer quantitativement les mesures de temps dans les deux trames inertielles, nous pouvons relier les distances de la Figure\(\PageIndex{1b}\) entre elles, puis exprimer chaque distance en termes de temps de trajet (respectivement l'un\(\Delta t\) ou l'autre\(\Delta \tau\)) de l'impulsion dans le référentiel correspondant. L'équation résultante peut ensuite être résolue\(\Delta t\) en termes de\(\Delta \tau\).

Les longueurs\(D\) et\(L\) sur la figure\(\PageIndex{1c}\) sont les côtés d'un triangle droit avec hypoténuse\(s\). D'après le théorème de Pythagore,

\[s^2 = D^2 + L^2. \nonumber \]

Les longueurs\(2s\) et\(2L\) sont, respectivement, les distances que l'impulsion lumineuse et l'engin spatial parcourent dans le temps\(\Delta t\) dans le cadre de l'observateur terrestre. La longueur\(D\) est la distance que l'impulsion lumineuse parcourt dans le temps\(\Delta \tau\) dans le cadre de l'astronaute. Cela nous donne trois équations :

\[\begin{align*} 2s &= c\Delta t \\[4pt] 2L &= v\Delta t; \\[4pt] 2D &= c\Delta \tau. \end{align*} \nonumber \]

Notez que nous avons utilisé le deuxième postulat d'Einstein en prenant la vitesse de la lumière comme c dans les deux cadres inertiels. Nous substituons ces résultats à l'expression précédente du théorème de Pythagore :

\[ \begin{align*} s^2 &= D^2 + L^2 \\[4pt] \left(c\dfrac{\Delta t}{2}\right)^2 &= \left(c\dfrac{\Delta \tau}{2}\right)^2 + \left(v\dfrac{\Delta t}{2}\right)^2 \end{align*} \nonumber \]

Ensuite, nous réorganisons pour obtenir

\[(c\Delta t)^2 - (v\Delta t)^2 = (c\Delta \tau)^2. \nonumber \]

Enfin, résoudre\(\Delta t\) en termes de nous\(\Delta \tau\) donne

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - (v/c)^2}}. \nonumber \]

Ceci est équivalent à

\[\Delta t = \gamma \Delta \tau, \label{timedilation} \]

où\(\gamma\) est le facteur relativiste (souvent appelé facteur de Lorentz) donné par

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} \nonumber \]

et\(v\) et\(c\) sont les vitesses de l'observateur en mouvement et de la lumière, respectivement.

Notez l'asymétrie entre les deux mesures. Un seul d'entre eux est la mesure de l'intervalle de temps entre deux événements, l'émission et l'arrivée de l'impulsion lumineuse, à la même position. Il s'agit d'une mesure de l'intervalle de temps dans la trame de repos d'une horloge unique. La mesure dans le cadre terrestre consiste à comparer l'intervalle de temps entre deux événements qui se produisent à des endroits différents. L'intervalle de temps entre les événements qui se produisent à un même endroit porte un nom distinct pour le distinguer du temps mesuré par l'observateur terrestre, et nous utilisons le symbole distinct\(\Delta \tau\) pour le désigner tout au long de ce chapitre.

Définition : Heure appropriée

L'intervalle de temps approprié\(\Delta \tau\) entre deux événements est l'intervalle de temps mesuré par un observateur pour lequel les deux événements se produisent au même endroit.

L'équation relative à\(\delta t\) et\(\Delta \tau\) est vraiment remarquable. Tout d'abord, comme indiqué précédemment, le temps écoulé n'est pas le même pour les différents observateurs se déplaçant l'un par rapport à l'autre, même si les deux se trouvent dans des trames inertielles. L'intervalle de temps approprié\(\Delta \tau\) pour un observateur qui, comme l'astronaute, se déplace avec l'appareil est plus court que l'intervalle de temps pour les autres observateurs. Il s'agit du plus petit temps mesuré possible entre deux événements. L'observateur terrestre voit les intervalles de temps au sein du système en mouvement comme dilatés (c'est-à-dire allongés) par rapport à la façon dont l'observateur se déplaçant par rapport à la Terre les perçoit dans le système en mouvement. Par ailleurs, selon l'observateur terrestre, moins de temps s'écoule entre les événements au sein du cadre mobile. Notez que le temps écoulé le plus court entre les événements se situe dans la trame inertielle dans laquelle l'observateur voit les événements (par exemple, l'émission et l'arrivée du signal lumineux) se produire au même point.

Cet effet de temps est réel et n'est pas dû à des horloges inexactes ou à des mesures incorrectes. Les mesures par intervalles de temps d'un même événement diffèrent pour les observateurs en mouvement relatif. La dilatation du temps est une propriété intrinsèque du temps lui-même. On observe que toutes les horloges qui se déplacent par rapport à un observateur, y compris les horloges biologiques, telles que le rythme cardiaque d'une personne ou le vieillissement, tournent plus lentement qu'une horloge fixe par rapport à l'observateur.

Notez que si la vitesse relative est bien inférieure à la vitesse de la lumière (v << c), elle\(v^2/c^2\) est extrêmement faible et les temps\(\Delta t\) écoulés\(\Delta \tau\) sont presque égaux. À basse vitesse, la physique basée sur la relativité moderne se rapproche de la physique classique : les expériences quotidiennes impliquent de très faibles effets relativistes. Cependant, pour des vitesses proches de la vitesse de la lumière,\(v^2/c^2\) est proche de 1,\(\sqrt{1 - v^2/c^2}\) il est donc très petit et\(\Delta t\) devient nettement supérieur à\(\Delta \tau\).

Demi-vie d'un muon

De nombreuses preuves expérimentales indiquent que l'équation\(\Delta t = \gamma \Delta \tau\) est correcte. On en trouve un exemple dans les particules de rayons cosmiques qui pleuvent continuellement sur Terre depuis l'espace lointain. Certaines collisions de ces particules avec des noyaux dans la haute atmosphère produisent des particules à courte durée de vie appelées muons. La demi-vie (durée pendant laquelle la moitié d'une matière se désintègre) est de 1,52 μs lorsqu'il est au repos par rapport à l'observateur qui mesure la demi-vie. Il s'agit de l'intervalle de temps approprié\(\Delta \tau\). Ce court laps de temps permet à très peu de muons d'atteindre la surface de la Terre et d'être détectés si les hypothèses newtoniennes concernant le temps et l'espace étaient correctes. Cependant, les muons produits par les particules des rayons cosmiques ont une gamme de vitesses, certains se déplaçant à une vitesse proche de celle de la lumière. Il a été découvert que la demi-vie du muon mesurée par un observateur terrestre (\(\Delta t\)) varie avec la vitesse exactement comme le prédit l'équation\(\Delta t = \gamma \Delta \tau\). Plus le muon se déplace rapidement, plus il vit longtemps. Sur Terre, nous voyons le muon durer bien plus longtemps que ne le prédit sa demi-vie dans son propre cadre de repos. Vu de notre cadre, le muon se désintègre plus lentement que lorsqu'il est au repos par rapport à nous. Il en résulte qu'une fraction beaucoup plus importante de muons atteint le sol.

Avant de présenter le premier exemple de résolution d'un problème en relativité, nous présentons une stratégie que vous pouvez utiliser comme guide pour ces calculs.

STRATÉGIE DE RÉSOLUTION DE PROBLÈMES : RELATIVITÉ

1. Dressez une liste de ce qui est indiqué ou peut être déduit du problème tel qu'indiqué (identifier les éléments connus). Recherchez en particulier des informations sur la vitesse relative v.
2. Identifiez exactement ce qui doit être déterminé dans le problème (identifiez les inconnues).
3. Assurez-vous de comprendre les aspects conceptuels du problème avant de faire des calculs (exprimez la réponse sous forme d'équation). Déterminez, par exemple, quel observateur voit le temps dilater ou la longueur se contracter avant de travailler avec les équations ou de les utiliser pour effectuer le calcul. Si vous vous êtes demandé qui voit quoi, qui se déplace en fonction de l'événement observé, qui voit le moment opportun, etc., il sera beaucoup plus facile de déterminer si votre calcul est raisonnable.
4. Déterminez le principal type de calcul à effectuer pour trouver les inconnues identifiées ci-dessus (faites le calcul). Vous trouverez le résumé de la section utile pour déterminer si une contraction de longueur, une énergie cinétique relativiste ou un autre concept est impliqué.

Notez que vous ne devez pas arrondir les points lors du calcul. Comme indiqué dans le texte, vous devez souvent effectuer vos calculs à plusieurs chiffres pour obtenir l'effet souhaité. Vous pouvez arrondir à la toute fin de la solution du problème, mais n'utilisez pas de nombre arrondi dans un calcul ultérieur. Vérifiez également la réponse pour voir si elle est raisonnable : est-ce logique ? Cela peut être plus difficile pour la relativité, qui ne dispose que de peu d'exemples quotidiens pour fournir de l'expérience avec ce qui est raisonnable. Mais vous pouvez rechercher des vitesses supérieures à c ou des effets relativistes qui vont dans la mauvaise direction (comme une contraction temporelle alors qu'une dilatation était attendue).

Exemple\(\PageIndex{1A}\): Time Dilation in a High-Speed Vehicle

Le Hypersonic Technology Vehicle 2 (HTV-2) est une fusée expérimentale capable de se déplacer à 21 000 km/h (5 830 m/s). Si une horloge électronique du HTV-2 mesure un intervalle de temps d'une durée exacte d'une seconde, comment les observateurs sur Terre mesureraient-ils cet intervalle de temps ?

Stratégie

Appliquez la formule de dilatation temporelle pour relier l'intervalle de temps approprié du signal dans HTV-2 à l'intervalle de temps mesuré au sol.

Solution

1. Identifier les éléments connus :\(\Delta \tau = 1 \, s\)\(v = 5830m/s.\)
2. Identifiez l'inconnu :\(\Delta t\).
3. Exprimez la réponse sous forme d'équation :

   \[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

4. Fais le calcul. Utilisez l'expression pour déterminer\(\gamma\) à\(\Delta t\) partir de\(\Delta \tau\) :

   \[\begin{align*} \Delta t &= \dfrac{1 \, s}{\sqrt{1 - \left(\dfrac{5830 \, m/s}{3.00 \times 10^8 m/s}\right)^2}} \\[4pt] &= 1.000000000189 \, s \\[4pt] &= 1 \, s + 1.89 \times 10^{-10}s. \end{align*} \nonumber \]

L'importance

La vitesse très élevée du HTV-2 n'est toujours que 10 à ⁵ fois la vitesse de la lumière. Les effets relativistes du HTV-2 sont négligeables à presque tous les égards, mais ils ne sont pas nuls.

Quelles vitesses sont relativistes ?

À quelle vitesse un véhicule doit-il parcourir pendant une seconde de temps, mesurée sur la montre d'un passager dans le véhicule, pour différer de 1 % pour un observateur qui la mesure depuis le sol à l'extérieur ?

Stratégie

Utilisez la formule de dilatation temporelle pour trouver v/c pour le ratio de temps donné.

Solution

1. Identifiez les éléments connus :

   \[\dfrac{\Delta \tau}{\Delta t} = \dfrac{1}{1.01}. \nonumber \]

2. Identifier l'inconnu : v/c.
3. Exprimez la réponse sous forme d'équation :

   \[ \begin{align*} \Delta t &= \gamma \Delta \tau \\[4pt] &= \dfrac{1}{\sqrt{1 - v^2/c^2}}\Delta \tau \\[4pt] \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 - v^2/c^2} \\[4pt] \left(\dfrac{\Delta \tau}{\Delta t}\right)^2 &= 1 - \dfrac{v^2}{c^2} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - (\Delta \tau/\Delta t)^2}. \end{align*} \nonumber \]

4. Effectuez le calcul :

   \[\dfrac{v}{c} = \sqrt{1 - (1/1.01)^2} = 0.14. \nonumber \]

L'importance

Le résultat montre qu'un objet doit se déplacer à environ 10 % de la vitesse de la lumière pour que son mouvement produise des effets relativistes de dilatation temporelle significatifs.

Calculer\(\Delta t\) en fonction d'un événement relativiste

Supposons qu'un rayon cosmique entre en collision avec un noyau situé dans la haute atmosphère de la Terre produise un muon ayant une certaine vitesse\(v = 0.950c\). Le muon se déplace ensuite à vitesse constante et vit 2,20 μs, tel que mesuré dans le cadre de référence du muon. (Vous pouvez l'imaginer comme l'horloge interne du muon.) Combien de temps vit le muon tel que mesuré par un observateur terrestre (Figure\(\PageIndex{2}\)) ?

Figure\(\PageIndex{2}\) : Un muon présent dans l'atmosphère de la Terre vit plus longtemps si l'on le mesure par un observateur terrestre que si l'horloge interne du muon le mesure.

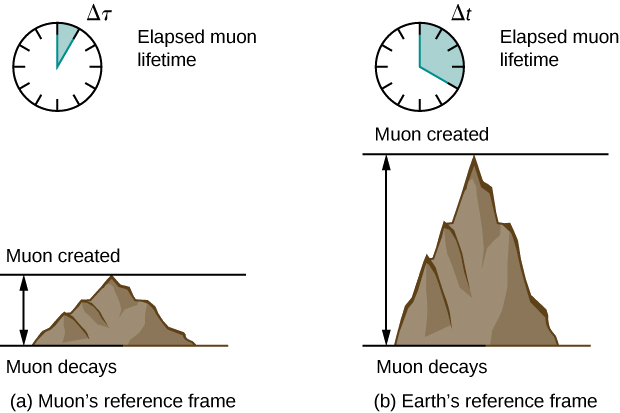
Comme nous le verrons plus loin, dans le référentiel du muon, il parcourt une distance plus courte que celle mesurée dans le référentiel de la Terre.

Stratégie

Une horloge qui se déplace avec le muon mesure le moment approprié de son processus de désintégration, donc le temps qui nous est accordé est égal à celui qui nous est accordé\(\Delta \tau = 2.20 \mu s\). L'observateur terrestre mesure\(\Delta t\) comme indiqué par l'équation\(\Delta t = \gamma \Delta \tau\). Comme la vitesse est donnée, nous pouvons calculer le temps dans le cadre de référence de la Terre.

Solution

1. Identifiez les connus :\(v = 0.950c\) ;\(\delta \tau = 2.20 \mu s\).
2. Identifiez l'inconnu :\(\Delta t\).
3. Exprimez la réponse sous forme d'équation. Utilisation :

   \[\Delta t = \gamma \Delta \tau. \nonumber \]

   avec

   \[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber \]

4. Fais le calcul. Utilisez l'expression pour déterminer\(\gamma\) à\(\Delta t\) partir de\(\Delta \tau\) :

   \[\begin{align*} \Delta t &= \gamma \Delta \tau. \\[4pt] &=\dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}\delta \tau \\[4pt] &=\dfrac{2.20 \mu s}{\sqrt{1 - (0.950)^2}} \\[4pt] &= 7.05 \, \mu s.\end{align*} \nonumber \]

   N'oubliez pas de conserver les chiffres supplémentaires significatifs jusqu'à la réponse finale.

L'importance

L'une des implications de cet exemple est qu'\(\gamma = 3.20\)à 95,0 % de la vitesse de la lumière (\(v = 0.950c\)), les effets relativistes sont significatifs. Les deux intervalles de temps diffèrent d'un facteur 3,20, alors qu'ils seraient classiquement identiques. On dit que quelque chose qui se déplace à 0,950 ° C est hautement relativiste.

Exemple\(\PageIndex{1B}\): Relativistic Television

Un écran de télévision non plat de style ancien (Figure\(\PageIndex{3}\)) fonctionne en accélérant les électrons sur une courte distance jusqu'à une vitesse relativiste, puis en utilisant des champs électromagnétiques pour contrôler l'endroit où le faisceau d'électrons frappe une couche fluorescente à l'avant du tube. Supposons que les électrons se\(6.00 \times 10^7 m/s\) déplacent à une distance de 0,200 m0,200 m entre le début du faisceau et l'écran.

1. Quel est le temps de trajet d'un électron dans le cadre de repos du téléviseur ?
2. Quel est le temps de trajet de l'électron dans son propre cadre de repos ?

Figure\(\PageIndex{3}\) : Le faisceau d'électrons sur un écran de télévision à tube cathodique.

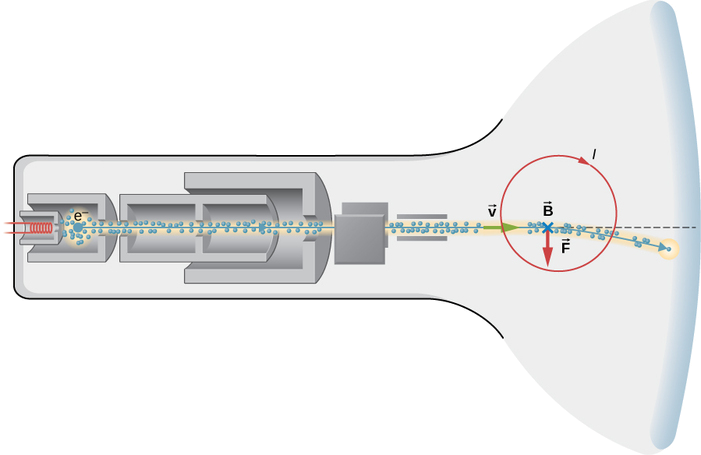
Stratégie pour (a)

(a) Calculez l'heure à partir de\(vt = d\). Même si la vitesse est relativiste, le calcul se fait entièrement dans un cadre de référence, et la relativité n'est donc pas impliquée.

Solution

1. Identifiez les éléments connus :

   \[v = 6.00 \times 10^7 m/s \, d = 0.200 \, m. \nonumber \]

2. Identifiez l'inconnu : l'heure du voyage\(\Delta t\).
3. Exprimez la réponse sous forme d'équation :

   \[\Delta t = \dfrac{d}{v}. \nonumber \]

4. Effectuez le calcul :

   \[ \begin{align*} t &= \dfrac{0.200 \, m}{6.00 \times 10^7 \, m/s} \\[4pt] &= 3.33 \times 10^{-9} \, s. \end{align*} \nonumber \]

L'importance

Le temps de trajet est extrêmement court, comme prévu. Comme le calcul s'inscrit entièrement dans un cadre de référence unique, la relativité n'est pas impliquée, même si la vitesse des électrons est proche de c.

Stratégie pour (b)

(b) Dans le cadre de référence de l'électron, le tube à vide se déplace et l'électron est stationnaire. La cathode émettrice d'électrons quitte l'électron et l'avant du tube à vide frappe l'électron avec l'électron au même endroit. Nous utilisons donc la formule de dilatation temporelle pour relier le temps approprié dans l'image de repos des électrons au temps dans l'image de télévision.

Solution

1. Identifiez les éléments connus (à partir de la partie a) :

   \[\Delta t = 3.33 \times 10^{-9} \, s; \, v = 6.00 \times 10^7 \, m/s; \, d = 0.200 \, m. \nonumber \]

2. Identifiez l'inconnu :\(\tau\).
3. Exprimez la réponse sous forme d'équation :

   \[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{1 - v^2/c^2}}. \nonumber \]

4. Effectuez le calcul :

   \[\begin{align*} \Delta \tau &= (3.33 \times 10^{-9}s)\sqrt{1 - \left(\dfrac{6.00 \times 10^7 m/s}{3.00 \times 10^8 m/s}\right)^2} \\[4pt] &= 3.26 \times 10^{-9}s. \end{align*} \nonumber \]

L'importance

Le temps de trajet est plus court dans le référentiel électronique. Comme le problème nécessite de trouver l'intervalle de temps mesuré dans différents référentiels pour le même processus, la relativité entre en jeu. Si nous avions essayé de calculer le temps dans la base de repos des électrons en divisant simplement 0,200 m par la vitesse, le résultat serait légèrement incorrect en raison de la vitesse relativiste de l'électron.

Exercice\(\PageIndex{1}\)

Qu'est-ce que c'est\(\gamma\) si\(v = 0.650c\) ?

Réponse

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \dfrac{(0.650c)}{c^2}}} = 1.32 \nonumber \]

Le double paradoxe

L'une des conséquences intrigantes de la dilatation du temps est qu'un voyageur spatial se déplaçant à une vitesse élevée par rapport à la Terre vieillirait moins que le jumeau terrestre de l'astronaute. C'est ce que l'on appelle souvent le double paradoxe. Imaginez que l'astronaute se déplace à une vitesse telle que\(\gamma = 30.0\), comme dans la Figure\(\PageIndex{4}\). Un voyage qui dure 2 ans dans son cadre prendrait 60 ans dans le cadre de la jumelle terrestre. Supposons que l'astronaute voyage 1 an vers un autre système stellaire, explore brièvement la région, puis voyage 1 an en arrière. Un astronaute âgé de 40 ans au début du voyage aurait 42 ans au retour du vaisseau spatial. Cependant, tout ce qui se trouve sur Terre aurait vieilli de 60 ans. Le jumeau terrestre, s'il était toujours vivant, aurait 100 ans.

La situation semblerait différente à l'astronaute de la figure\(\PageIndex{4}\). Comme le mouvement est relatif, le vaisseau spatial semble immobile et la Terre semble bouger. (C'est la sensation que vous ressentez lorsque vous volez à bord d'un jet.) En regardant par la fenêtre du vaisseau spatial, l'astronaute verrait le temps ralentir sur Terre d'un facteur\(\gamma = 30.0\). Vu du vaisseau spatial, le frère terrestre n'aura que 2/30 ans, soit 0,07, par an, alors que l'astronaute aurait atteint l'âge de 2 ans.

Figure\(\PageIndex{4}\) : Le double paradoxe consiste en des conclusions contradictoires quant à savoir quel jumeau vieillit le plus à la suite d'un long voyage dans l'espace à une vitesse relativiste.

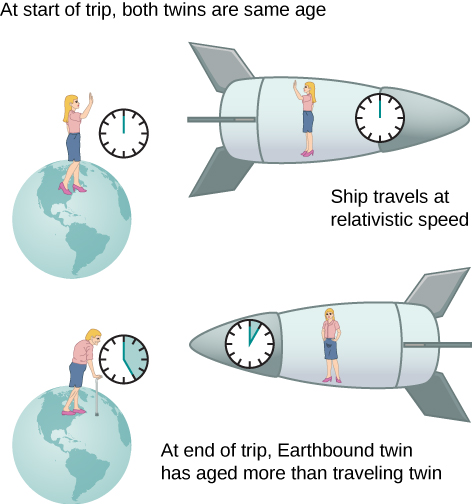
Le paradoxe ici est que les deux jumeaux ne peuvent pas tous deux être corrects. Comme pour tous les paradoxes, les conclusions contradictoires découlent d'une fausse prémisse. En fait, le mouvement de l'astronaute est très différent de celui du jumeau terrestre. L'astronaute accélère à grande vitesse, puis décélère pour observer le système stellaire. Pour revenir sur Terre, elle accélère et décélère à nouveau. L'engin spatial ne se trouve pas dans un cadre inertiel unique auquel la formule de dilatation temporelle peut être directement appliquée. C'est-à-dire que le jumeau de l'astronaute change les références inertielles. Le jumeau terrestre ne subit pas ces accélérations et reste dans le même cadre inertiel. La situation n'est donc pas symétrique et il est faux de prétendre que l'astronaute observe les mêmes effets que sa jumelle. Le manque de symétrie entre les jumeaux sera encore plus évident lorsque nous analyserons le voyage plus loin dans ce chapitre en termes de trajectoire que suit l'astronaute dans l'espace-temps en quatre dimensions.

En 1971, les physiciens américains Joseph Hafele et Richard Keating ont vérifié la dilatation du temps à de faibles vitesses relatives en faisant voler des horloges atomiques extrêmement précises dans le monde entier à bord d'avions commerciaux. Ils ont mesuré le temps écoulé avec une précision de quelques nanosecondes et l'ont comparé au temps mesuré par des horloges laissées derrière elles. Les résultats de Hafele et Keating se situaient dans les limites des incertitudes expérimentales quant aux prédictions de la relativité. La relativité spéciale et la relativité générale devaient être prises en compte, car la gravité et les accélérations étaient impliquées ainsi que le mouvement relatif.

Exercice\(\PageIndex{2A}\)

a. Une particule se déplace\(1.90 \times 10^8 \, m/s\) et vit\(2.1 \times 10^8 \, s\) au repos par rapport à un observateur. Quelle est la durée de vie de la particule observée en laboratoire ?

Réponse

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{2.10 \times 10^{-8}s}{\sqrt{1 - \dfrac{(1.90 \times 10^8 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 2.71 \times 10^{-8} \, s. \nonumber \]

Exercice\(\PageIndex{2B}\)

Les vaisseaux spatiaux A et B passent dans des directions opposées à une vitesse relative de\(4.00 \times 10^7 \, m/s\). Une horloge interne de l'engin A émet un signal radio pendant 1 seconde. L'ordinateur de l'engin B corrige le début et la fin du signal après avoir parcouru différentes distances, afin de calculer l'intervalle de temps pendant lequel le navire A a émis le signal. Quel est l'intervalle de temps calculé par l'ordinateur de l'engin spatial B ?

Réponse

Seule la vitesse relative des deux engins spatiaux est importante, car il n'y a pas de mouvement absolu dans l'espace. Le signal est émis à partir d'un emplacement fixe dans le référentiel de A, de sorte que l'intervalle de temps approprié pour son émission est\(\tau = 1.00 \, s\). La durée du signal mesuré à partir du référentiel B est alors

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1.00 \, s}{\sqrt{1 - \dfrac{(4.00 \times 10^7 \, m/s)^2}{(3.00 \times 10^8 \, m/s)^2}}} = 1.01 \, s. \nonumber \]