B : Principes de base des mathématiques
- Page ID
- 187837
Carrés et autres pouvoirs
Un exposant, ou une puissance, est un raccourci mathématique désignant des multiplications répétées. Par exemple, l'exposant « 2 » signifie multiplier la base de cet exposant par lui-même (dans l'exemple ici, la base est « 5 ») :
\[5^2=5×5=25\]
L'exposant est « 2 » et la base est le nombre « 5 ». Cette expression (multiplication d'un nombre par elle-même) est également appelée carré. Tout nombre élevé à la puissance de 2 est mis au carré. Tout nombre porté à la puissance de 3 est coupé au cube :
\[5^3=5×5×5=125\]
Un nombre élevé à la quatrième puissance est égal à ce nombre multiplié par lui-même quatre fois, et ainsi de suite pour les puissances supérieures. En général :
\[n^x=n×n^{x−1}\]
Calcul des pourcentages
Un pourcentage est une façon d'exprimer une fraction de quelque chose en utilisant un tout divisé en 100 parties. Un pourcentage est un ratio dont le dénominateur est 100. Nous utilisons le symbole du pourcentage, %, pour afficher le pourcentage. Ainsi, 25 % signifie un ratio de\(\frac{25}{100}\), 3 % signifie un ratio de\(\frac{3}{100}\), et 100 % signifie\(\frac{100}{100}\), ou un tout.
Pourcentage de conversion
Un pourcentage peut être converti en fraction en écrivant la valeur du pourcentage sous la forme d'une fraction avec un dénominateur de 100 et en simplifiant la fraction si possible.
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
Un pourcentage peut être converti en décimal en écrivant la valeur du pourcentage sous forme de fraction avec un dénominateur de 100 et en divisant le numérateur par le dénominateur.
\[10\%=\dfrac{10}{100}=0.10\]
Pour convertir une décimale en pourcentage, écrivez la décimale sous forme de fraction. Si le dénominateur de la fraction n'est pas 100, convertissez-la en une fraction avec un dénominateur de 100, puis écrivez la fraction sous forme de pourcentage.
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
Pour convertir une fraction en pourcentage, convertissez d'abord la fraction en décimal, puis convertissez la décimale en pourcentage.
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
Supposons qu'un chercheur découvre que 15 élèves sur 23 d'une classe sont porteurs de Neisseria meningitides. Quel est le pourcentage d'étudiants porteurs ? Pour trouver cette valeur, exprimez d'abord les nombres sous forme de fraction.
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
Divisez ensuite le numérateur par le dénominateur.
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
Enfin, pour convertir un nombre décimal en pourcentage, multipliez-le par 100.
\[0.65 \times 100=65\%\]
Le pourcentage d'étudiants porteurs est de 65 %.
Vous pouvez également obtenir des données sur l'occurrence et la non-occurrence ; par exemple, sur un échantillon d'étudiants, 9 ont donné des résultats positifs pour les anticorps anti-toxoplasme, tandis que 28 ont donné des résultats négatifs. Quel est le pourcentage d'élèves séropositifs ? La première étape consiste à déterminer le « tout », dont font partie les élèves positifs. Pour ce faire, additionnez les tests positifs et négatifs.
\[\mathrm{positive+negative=9+28=37}\]
L'ensemble de l'échantillon était composé de 37 étudiants. La fraction de points positifs est la suivante :
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
Pour déterminer le pourcentage d'élèves porteurs, divisez le numérateur par le dénominateur et multipliez-le par 100.
\ [\ dfrac {9} {37} =9 \ div 37 \ environ 0,24 \ \
0,24 \ fois 100 = 24 \ % \]
Le pourcentage d'élèves positifs est d'environ 24 %.
Une autre façon de calculer un pourcentage consiste à définir des fractions équivalentes, dont l'une est une fraction avec 100 comme dénominateur, et à effectuer une multiplication croisée. L'exemple précédent serait exprimé comme suit :
\[\dfrac{9}{37}=\dfrac{x}{100}\]
Maintenant, croisez, multipliez et résolvez l'inconnu :
\ [\ begin {align}
9 \ times 100 &=37 x & & & \ nonumber \ \ [5pt]
\ frac {9 \ times 100} {37} &=x & & \ text {Divisez les deux côtés par 37} \ nonumber \ \ [5 points] \ frac {900} {37} &=x & & \ text {Multipliez} \ nonumber
\ \ [5 points] \ frac {900} {37} &=x & & \ text {Multipliez} \ nonumber \ \ [5 points]
\ frac {900} {37} &=x & & & \ text {Diviser} \ nonumber
\ end {align} \]
La réponse, arrondie, est la même.
Multiplier et diviser par dizaines
Dans de nombreux domaines, notamment en sciences, il est courant de multiplier les décimales par des puissances de 10. Voyons ce qui se passe lorsque nous multiplions 1,9436 par quelques puissances de 10.
\ [\ begin {align}
1.9436 (10) &=19,436 \ nonnumber \ \
1.9436 (100) &=194,36 \ nonnumber \ \
1.9436 (1000) &=1943,6 \ nonnumber
\ end {align} \]
Le nombre de positions que la virgule décimale déplace est identique au nombre de zéros de la puissance de dix. Le tableau\(\PageIndex{1}\) résume les résultats.
| Multipliez par | Zéros | Déplace la virgule décimale... |
|---|---|---|
| 10 | 1 | 1 place vers la droite |
| 100 | 2 | 2 places vers la droite |
| 1 000 | 3 | 3 places vers la droite |
| 10 000 | 4 | 4 places vers la droite |
Nous pouvons utiliser ce modèle comme raccourci pour multiplier par des puissances de dix au lieu de multiplier en utilisant le format vertical. Nous pouvons compter les zéros avec la puissance de 10, puis déplacer la virgule décimale du même nombre de places vers la droite.
Ainsi, par exemple, pour multiplier 45,86 par 100, déplacez la virgule décimale de 2 places vers la droite.
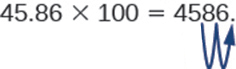
Parfois, lorsque nous devons déplacer le point décimal, il n'y a pas assez de décimales. Dans ce cas, nous utilisons des zéros comme espaces réservés. Par exemple, multiplions 2,4 par 100. Nous devons déplacer la virgule décimale de 2 places vers la droite. Comme il n'y a qu'un seul chiffre à droite de la virgule décimale, il faut écrire un 0 au centième.
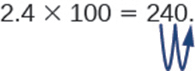
Lorsque vous divisez par des puissances de 10, adoptez simplement l'approche inverse et déplacez la décimale vers la gauche du nombre de zéros de la puissance de dix.
Voyons ce qui se passe lorsque nous divisons 1,9436 par quelques puissances de 10.
\ [\ begin {align}
1.9436 \ div 10&=0.19436 \ nonumber \ \
1.9436 \ div 100&=0.019436 \ nonnumber \ \
1.9436 \ div 1000&=0,0019436 \ nonumber
\ end {align} \]
S'il n'y a pas suffisamment de chiffres pour déplacer la décimale, ajoutez des zéros pour créer des places.
Notation scientifique
La notation scientifique est utilisée pour exprimer de très grands et de très petits nombres sous forme de produit de deux nombres. Le premier chiffre du produit, le terme numérique, est généralement un nombre compris entre 1 et 10. Le deuxième nombre du produit, le terme exponentiel, s'écrit 10 avec un exposant. Quelques exemples de notation scientifique sont donnés dans le tableau\(\PageIndex{2}\).
| Notation standard | Notation scientifique |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0,1 | 1 × 10 −1 |
| 0,01 | 1 × 10 −2 |
La notation scientifique est particulièrement utile pour les très grands et très petits nombres, tels que 1 230 000 000 = 1,23 × 10 9 et 0,000000036 = 3,6 × 10 −10.
Expression de nombres en notation scientifique
La conversion de n'importe quel nombre en notation scientifique est simple. Comptez le nombre de places nécessaires pour déplacer la décimale à côté du chiffre différent de zéro le plus à gauche, c'est-à-dire pour que le nombre soit compris entre 1 et 10. Multipliez ensuite ce nombre par 10, augmenté jusqu'au nombre de positions où vous avez déplacé la décimale. L'exposant est positif si vous avez déplacé la décimale vers la gauche et négatif si vous avez déplacé la décimale vers la droite. Donc
\[2386=2.386\times1000=2.386\times10^3\]
et
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
La puissance (exposant) de 10 est égale au nombre de décimales décalées.
Logarithmes
Le logarithme commun (log) d'un nombre est la puissance à laquelle 10 doit être élevé pour être égal à ce nombre. Par exemple, le logarithme commun de 100 est 2, car 10 doit être élevé à la deuxième puissance pour être égal à 100. Des exemples supplémentaires se trouvent dans le tableau\(\PageIndex{3}\).
| Numéro | Forme exponentielle | Logarithme commun |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0,1 | 10 −1 | −1 |
| 0,001 | 10 −3 | −3 |
Pour trouver le logarithme commun à la plupart des nombres, vous devez utiliser le bouton LOG d'une calculatrice.
Chiffres arrondis et significatifs
Pour communiquer les données numériques obtenues par le biais de mesures, nous utilisons uniquement autant de chiffres significatifs que la précision des mesures le justifie. Supposons, par exemple, qu'un microbiologiste utilise un compteur automatique de cellules pour déterminer qu'il y a 525 341 cellules bactériennes dans un échantillon d'un litre d'eau de rivière. Cependant, elle enregistre la concentration à 525 000 cellules par litre et utilise ce nombre arrondi pour estimer le nombre de cellules qui se trouveraient probablement dans 10 litres d'eau de rivière. Dans ce cas, les trois derniers chiffres de la quantité mesurée ne sont pas considérés comme significatifs. Ils sont arrondis pour tenir compte des variations du nombre de cellules qui se produiraient probablement si davantage d'échantillons étaient mesurés.
L'importance des chiffres significatifs réside dans leur application au calcul fondamental. En plus de la soustraction, la somme ou la différence doit contenir autant de chiffres à droite de la décimale que le nombre le moins certain (indiqué par un trait de soulignement dans l'exemple suivant) des nombres utilisés dans le calcul.
Supposons qu'un microbiologiste souhaite calculer la masse totale de deux échantillons de gélose.
\ [\ begin {array} {l}
4,38 \ underline {3} \ text {g} \ \
\ underline {3.002 \ underline {1}} \ text {g} \ \
7,38 \ underline {5} \ text {g}
\ end {array} \]
La moins certaine des deux masses possède trois décimales, de sorte que la somme doit comporter trois décimales.
Lors de la multiplication et de la division, le produit ou le quotient ne doit pas contenir plus de chiffres que le facteur contenant le moins de chiffres significatifs. Supposons que le microbiologiste souhaite calculer la quantité de réactif qui serait présente dans 6,6 ml si la concentration est de 0,638 g/mL.
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
Encore une fois, la réponse ne comporte qu'une décimale, car il s'agit de la précision du nombre le moins précis dans le calcul.
Lorsque vous arrondissez des nombres, augmentez le chiffre retenu de 1 s'il est suivi d'un nombre supérieur à 5 (« arrondir »). Ne modifiez pas le chiffre retenu si les chiffres qui suivent sont inférieurs à 5 (« arrondi vers le bas »). Si le chiffre retenu est suivi de 5, arrondissez vers le haut si le chiffre retenu est impair, ou arrondissez vers le bas s'il est pair (après arrondissement, le chiffre retenu sera donc toujours pair).
Durée d'une génération
Il est possible d'écrire une équation pour calculer le nombre de cellules à tout moment si le nombre de cellules de départ et le temps de doublement sont connus, à condition que les cellules se divisent à un rythme constant. Nous définissons N 0 comme le nombre de départ de bactéries, le nombre à l'instant t = 0. N i est le nombre de bactéries au temps t = i, un moment arbitraire dans le futur. Enfin, nous définirons j comme étant égal au nombre de générations, ou au nombre de fois que la population de cellules double pendant l'intervalle de temps. Ensuite, nous avons,
\[N_i=N_0\times2^j\]
Cette équation est une expression de la croissance par fission binaire.
Dans notre exemple, N 0 = 4, le nombre de générations, j, est égal à 3 après 90 minutes car le temps de génération est de 30 minutes. Le nombre de cellules peut être estimé à l'aide de l'équation suivante :
\ [\ begin {align}
N_I&=N_0 \ times2^j \ nonumber \ \
N_ {90} &=4 \ times2^3 \ nonnumber \ \
N_ {90} &=4 \ times8=32 \ nonnumber
\ end {align} \]
Le nombre de cellules après 90 minutes est de 32.
Nombre le plus probable
Le tableau de la figure\(\PageIndex{1}\) contient les valeurs utilisées pour calculer l'exemple de nombre le plus probable donné dans How Microbes Grow.