5.2 : La distribution uniforme
- Page ID
- 191665
La distribution uniforme est une distribution de probabilité continue qui concerne les événements qui sont également susceptibles de se produire. Lorsque vous résolvez des problèmes qui ont une distribution uniforme, veillez à noter si les données incluent ou excluent les points de terminaison.
L'énoncé mathématique de la distribution uniforme est
\(f(x) = \frac{1}{b-a}\)pour\(a \leq x \leq b\)
où\(a =\) la valeur la plus faible\(x\) et\(b =\) la valeur la plus élevée de\(x\).
Les formules pour la moyenne théorique et l'écart type sont les suivantes :
\(\mu=\frac{a+b}{2}\)et\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}\)
Exercice\(\PageIndex{1}\)
Les données suivantes sont le nombre de passagers sur 35 bateaux de pêche affrétés différents. La moyenne de l'échantillon = 7,9 et l'écart type de l'échantillon = 4,33. Les données suivent une distribution uniforme où toutes les valeurs comprises entre zéro et 14 inclus sont également probables. Indiquez les valeurs de\(a\) et\(b\). Écrivez la distribution dans la notation appropriée et calculez la moyenne théorique et l'écart type.
\ (\ PageIndex {1} \) « >| 1 | 12 | 4 | 10 | 4 | 14 | 11 |
| 7 | 11 | 4 | 13 | 2 | 4 | 6 |
| 3 | 10 | 0 | 12 | 6 | 9 | 10 |
| 5 | 13 | 4 | 10 | 14 | 12 | 11 |
| 6 | 10 | 11 | 0 | 11 | 13 | 2 |
-
Tableau 5.1
Exemple\(\PageIndex{2}\)
Le temps, exprimé en minutes, pendant lequel une personne doit attendre un bus est réparti uniformément entre zéro et 15 minutes, inclusivement.
a. Quelle est la probabilité qu'une personne attende moins de 12,5 minutes ?
- Réponse
-
a. Soit le\(X\) nombre de minutes pendant lesquelles une personne doit attendre un bus. \(a = 0\)et\(b = 15\). \(X \sim U(0, 15)\). Ecrivez la fonction de densité de probabilité. \(f(x) = \frac{1}{15-0}=\frac{1}{15}\)pour\(0 \leq x \leq 15\).
Trouve\(P(x < 12.5)\). Dessine un graphique.
\[P(x<k)=\text { (base) (height) }=(12.5-0)\left(\frac{1}{15}\right)=0.8333\nonumber\]
La probabilité qu'une personne attende moins de 12,5 minutes est de 0,8333.
Graphique 5.11
b. En moyenne, combien de temps une personne doit-elle attendre ? Trouvez la moyenne\(\mu\), et l'écart type,\(\sigma\).
- Réponse
-
\(\mu=\frac{a+b}{2}=\frac{15+0}{2}=7.5\)b. En moyenne, une personne doit attendre 7,5 minutes.
\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}=\sqrt{\frac{(15-\theta)^{2}}{12}}=4.3\). L'écart type est de 4,3 minutes.
c. Quatre-vingt-dix pour cent du temps, le temps qu'une personne doit attendre est inférieur à quelle valeur ?
Remarque
Cela demande le 90e percentile.
- Réponse
-
c. Déterminez le 90e percentile. Dessine un graphique. Soit\(k =\) le 90 e percentile.
\ (P) (x )<k) >
\(0.90=(k)\left(\frac{1}{15}\right)\)
\(k=(0.90)(15)=13.5\)
Le 90e percentile est de 13,5 minutes. Quatre-vingt-dix pour cent du temps, une personne doit attendre au plus 13,5 minutes.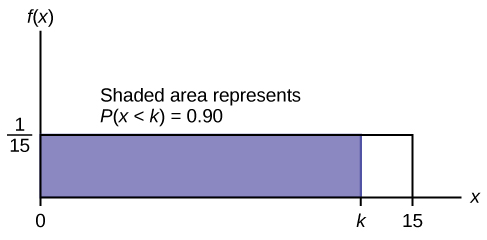 Figurine\(\PageIndex{12}\)
Figurine\(\PageIndex{12}\)
Exercice\(\PageIndex{2}\)
La durée totale des matchs de baseball dans les ligues majeures lors de la saison 2011 est uniformément répartie entre 447 heures et 521 heures inclusivement.
- Trouvez\(a\)\(b\) et décrivez ce qu'ils représentent.
- Écrivez la distribution.
- Détermine la moyenne et l'écart type.
- Quelle est la probabilité que la durée des matchs d'une équipe pour la saison 2011 se situe entre 480 et 500 heures ?


