17.4 : Solutions en séries d'équations différentielles
- Page ID
- 197496
- Utilisez des séries de puissance pour résoudre des équations différentielles du premier et du second ordre.
Auparavant, nous avons étudié comment les fonctions peuvent être représentées sous forme de séries de puissances,\(\displaystyle y(x)=\sum_{n=0}^{\infty} a_nx^n\). Nous avons également vu que nous pouvions trouver des représentations en série des dérivées de telles fonctions en différenciant les séries de puissance terme par terme. Cela donne
\[y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber \]
et
\[y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber \]
Dans certains cas, ces représentations de séries de puissances peuvent être utilisées pour trouver des solutions à des équations différentielles.
Les exemples et les exercices de cette section ont été choisis pour lesquels des solutions d'alimentation existent. Cependant, les solutions d'alimentation n'existent pas toujours. Ceux d'entre vous qui souhaitent un traitement plus rigoureux de ce sujet devraient consulter la section des équations différentielles des LibreTexts.
- Supposons que l'équation différentielle ait une solution de la forme\[y(x)=\sum_{n=0}^{\infty}a_nx^n. \nonumber \]
- Différenciez la série de puissance terme par terme pour obtenir\[y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber \] et\[y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber \]
- Substituez les expressions de la série de puissances dans l'équation différentielle.
- Réindexez les sommes si nécessaire pour combiner les termes et simplifier l'expression.
- Associez des coefficients de puissances similaires\(x\) à afin de déterminer les valeurs des coefficients\(a_n\) de la série de puissances.
- Remplacez les coefficients dans la série de puissances et écrivez la solution.
Trouvez une solution de série de puissance pour les équations différentielles suivantes.
- \(y''−y=0\)
- \((x^2−1)y″+6xy′+4y=−4\)
Solution
Partie a
Supposer
\[y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1} \]
Ensuite,
\[y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2A} \]
et
\[y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2B} \]
Nous voulons trouver des valeurs pour les coefficients\(a_n\) telles que
\[\begin{align*} &y″−y =0 \\[4pt] &\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}−\sum_{n=0}^{∞}a_nx^n =0 \tag{step 3}. \end{align*} \]
Nous voulons que les indices de nos sommes correspondent afin de pouvoir les exprimer en utilisant une seule sommation. C'est-à-dire que nous voulons réécrire la première sommation pour qu'elle commence par\(n=0\).
Pour réindexer le premier terme, remplacez-le\(n\) par\(n+2\) l'intérieur de la somme et remplacez la limite inférieure de sommation par\(n=0.\) We get
\[\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}=\sum_{n=0}^∞ (n+2)(n+1)a_{n+2}x^n. \nonumber \]
Cela donne
\[\begin{align*}\sum_{n=0}^{∞}(n+2)(n+1)a_{n+2}x^n−\sum_{n=0}^{∞}a_nx_n &=0 \\[4pt] \sum_{n=0}^{∞}[(n+2)(n+1)a_{n+2}−a_n]x^n &=0 \tag{step 4}.\end{align*} \]
Les extensions des fonctions en série de puissances étant uniques, cette équation ne peut être vraie que si les coefficients de chaque puissance de\(x\) sont nuls. Nous avons donc
\[(n+2)(n+1)a_{n+2}−a_n=0 \text{ for }n=0,1,2,…. \nonumber \]
Cette relation de récurrence nous permet d'exprimer chaque coefficient\(a_n\) en fonction du coefficient deux termes plus tôt. Cela donne une expression pour les valeurs paires de\(n\) et une autre pour les valeurs impaires de\(n\). En regardant d'abord les équations impliquant des valeurs paires de\(n\), nous voyons que
\[\begin{align*}a_2 &= \dfrac{a_0}{2} \\[5pt] a_4 &= \dfrac{a_2}{4⋅3} = \dfrac{a_0}{4!}\\[5pt] a_6 &= \dfrac{a_4}{6⋅5} =\dfrac{a_0}{6!} \\ &\qquad ⋮ \end{align*}\]
Ainsi, en général, lorsqu'il\(n\) est égal,
\[a_n=\dfrac{a_0}{n!}. \tag{step 5} \]
Pour les équations impliquant des valeurs impaires de,\(n,\) nous voyons que
\[\begin{align*}a_3 &=\dfrac{a_1}{3⋅2}=\dfrac{a_1}{3!} \\[5pt] a_5 &= \dfrac{a_3}{5⋅4}=\dfrac{a_1}{5!} \\[5pt] a_7 &= \dfrac{a_5}{7⋅6}=\dfrac{a_1}{7!} \\ &\qquad ⋮ \end{align*}\]
Donc, en général, quand\(n\) c'est étrange,
\[a_n=\dfrac{a_1}{n!}. \tag{step 5} \]
En rassemblant tout cela, nous avons
\[\begin{align*}y(x) &= \sum_{n=0}^{∞}a_nx^n \\[4pt] &=a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯. \end{align*}\]
En réindexant les sommes pour tenir compte des valeurs paires et impaires de\(n\) séparément, nous obtenons
\[y(x)=a_0 \sum_{k=0}^{∞} \dfrac{1}{(2k)!}x^{2k}+a_1 \sum_{k=0}^{∞}\dfrac{1}{(2k+1)!}x^{2k+1}. \tag{step 6} \]
Analyse pour la partie a.
Comme prévu pour une équation différentielle du second ordre, cette solution dépend de deux constantes arbitraires. Cependant, notez que notre équation différentielle est une équation différentielle à coefficient constant, mais que la solution des séries de puissance ne semble pas avoir la forme familière (contenant des fonctions exponentielles) que nous avons l'habitude de voir. De plus, comme\(y(x)=c_1e^x+c_2e^{−x}\) c'est la solution générale à cette équation, nous devons être en mesure d'écrire n'importe quelle solution sous cette forme, et il n'est pas clair si la solution de la série de puissance que nous venons de trouver peut, en fait, être écrite sous cette forme.
Heureusement, après avoir écrit les représentations des séries de puissance de\(e^x\)\(e^{−x},\) et fait de l'algèbre, nous constatons que si nous choisissons
\[c_0=\dfrac{(a_0+a_1)}{2}, c_1=\dfrac{(a_0−a_1)}{2}, \nonumber \]
nous avons alors\(a_0=c_0+c_1\) et\(a_1=c_0−c_1,\) et
\[\begin{align*}y(x) &= a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯ \\[4pt] &=(c_0+c_1)+(c_0−c_1)x+\dfrac{(c_0+c_1)}{2}x^2+\dfrac{(c_0−c_1)}{3!}x^3+\dfrac{(c_0+c_1)}{4!}x^4+\dfrac{(c_0−c_1)}{5!}x^5+⋯\\[4pt] &=c_0 \sum_{n=0}^{∞} \dfrac{x^n}{n!}+c_1 \sum_{n=0}^{∞}\dfrac{(−x)^n}{n!} \\[4pt] &=c_0e^x+c_1e^{−x}.\end{align*}\]
Nous avons donc trouvé la même solution générale. Notez que ce choix de\(c_1\) et n'\(c_2\)est pas évident. C'est un cas où nous savons quelle devrait être la réponse et que nous avons essentiellement « rétroconçu » notre choix de coefficients.
Partie B
Supposer
\[y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1} \]
Ensuite,
\[y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2} \]
et
\[y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2} \]
Nous voulons trouver des valeurs pour les coefficients\(a_n\) telles que
\[\begin{align*}(x^2−1)y″+6xy′+4y &=−4 \\ (x^2−1) \sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4 \\[4pt] x^2 \sum_{n=2}^{∞} n(n−1)a_nx^{n−2}−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4. \end{align*}\]
En prenant les facteurs externes à l'intérieur des sommations, nous obtenons
\[\sum_{n=2}^{∞}n(n−1)a_nx^n−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+\sum_{n=1}^∞ 6na_nx^n+ \sum_{n=0}^∞ 4a_nx^n=−4 \tag{step 3}. \]
Maintenant, dans la première sommation, nous voyons que lorsque\(n=0\) ou\(n=1\), le terme est évalué à zéro, nous pouvons donc rajouter ces termes à notre somme pour obtenir
\[\sum_{n=2}^{∞}n(n−1)a_nx^n=\sum_{n=0}^∞ n(n−1)a_nx^n. \nonumber \]
De même, dans le troisième terme, nous voyons que lorsque\(n=0\), l'expression est évaluée à zéro, nous pouvons donc également ajouter ce terme. Nous avons
\[\sum_{n=1}^∞ 6na_nx^n=\sum_{n=0}^∞6na_nx^n. \nonumber \]
Ensuite, il ne nous reste plus qu'à modifier les indices lors de notre second mandat. Nous obtenons
\[\sum_{n=2}^∞n(n−1)a_nx^{n−2}=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n. \nonumber \]
Ainsi, nous avons
\[\begin{align*} \sum_{n=0}^∞n(n−1)a_nx^n−\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n+\sum_{n=0}^∞6na_nx^n+\sum_{n=0}^∞4a_nx^n &=−4 \tag{step 4} \\[4pt] \sum_{n=0}^∞[n(n−1)a_n−(n+2)(n+1)a_{n+2}+6na_n+4a_n]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n^2−n)a_n+6na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[n^2a_n+5na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞ [(n^2+5n+4)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \end{align*} \]
En regardant les coefficients de chaque puissance de\(x\), nous voyons que le terme constant doit être égal à\(−4\) zéro et que les coefficients de toutes les autres puissances de\(x\) doivent être nuls. Ensuite, en examinant d'abord le terme constant,
\[\begin{aligned}4a_0−2a_2 &=−4 \\ a_2 &=2a_0+2 \end{aligned} \tag{step 3} \]
Pour\(n≥1\), nous avons
\[\begin{align*}(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2} &= 0 \\[4pt] (n+1)[(n+4)a_n−(n+2)a_{n+2}] &=0. \end{align*}\]
Puisque\(n≥1, \; n+1≠0,\) nous voyons que
\[(n+4)a_n−(n+2)a_{n+2}=0 \nonumber \]
et donc
\[a_{n+2}=\dfrac{n+4}{n+2}a_n. \nonumber \]
Pour des valeurs égales de\(n\), nous avons
\[\begin{align*} a_4 &=\dfrac{6}{4}(2a_0+2)=3a_0+3 \\ a_6 &= \dfrac{8}{6}(3a_0+3)=4a_0+4 \\[4pt] &\qquad ⋮ \end{align*}\]
En général,
\[a_{2k}=(k+1)(a_0+1). \tag{step 5} \]
Pour les valeurs impaires de\(n,\) nous avons
\[\begin{align*}a_3 &=\dfrac{5}{3}a_1 \\[4pt] a_5 &= \dfrac{7}{5}a_3=\dfrac{7}{3}a_1 \\[4pt] a_7 &=\dfrac{9}{7}a_5=\dfrac{9}{3} a_1=3a_1 \\[4pt] &\qquad ⋮ \end{align*}\]
En général,
\[a_{2k+1}=\dfrac{2k+3}{3}a_1. \tag{step 5 continued} \]
En rassemblant tout cela, nous avons
\[y(x)=\sum_{k=0}^∞ (k+1)(a_0+1)x^{2k}+\sum_{k=0}^∞ (\dfrac{2k+3}{3})a_1x^{2k+1}. \tag{step 6} \]
Trouvez une solution de série de puissance pour les équations différentielles suivantes.
- \(y′+2xy=0\)
- \((x+1)y′=3y\)
- Allusion
-
Suivez la stratégie de résolution des problèmes.
- Répondez à une
-
\(\displaystyle y(x)=a_0 \sum_{n=0}^∞ \dfrac{(−1)^n}{n!}x^{2n}=a_0e^{−x^2}\)
- Réponse b
-
\(y(x)=a_0(x+1)^3\)
Fonctions de Bessel
Nous clôturons cette section par une brève présentation des fonctions de Bessel. Le traitement complet des fonctions de Bessel dépasse largement le cadre de ce cours, mais nous avons ici un petit avant-goût du sujet afin de voir comment les solutions en série aux équations différentielles sont utilisées dans des applications réelles. L'équation d'ordre de Bessel\(n\) est donnée par
\[x^2y″+xy′+(x^2−n^2)y=0. \nonumber \]
Cette équation apparaît dans de nombreuses applications physiques, en particulier celles impliquant des coordonnées cylindriques, telles que la vibration d'une tête de tambour circulaire et le chauffage ou le refroidissement transitoires d'un cylindre. Dans l'exemple suivant, nous trouvons une solution de série de puissances à l'équation de Bessel d'ordre 0.
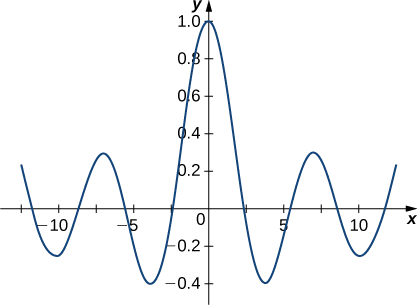
Trouvez une solution de série de puissances à l'équation de Bessel d'ordre 0 et représentez la solution sous forme graphique.
Solution
L'équation de Bessel d'ordre 0 est donnée par
\[x^2y″+xy′+x^2y=0. \nonumber \]
Nous supposons une solution du formulaire\(\displaystyle y=\sum_{n=0}^∞ a_nx^n\). Ensuite,\(\displaystyle y′(x)=\sum_{n=1}^∞ na_nx^{n−1}\) et en\(\displaystyle y''(x)=\sum_{n=2}^∞n(n−1)a_nx^{n−2}.\) substituant cela dans l'équation différentielle, nous obtenons
\[\begin{align*} x^2 \sum_{n=2}^∞ n(n−1)a_nx^{n−2}+x \sum_{n=1}^∞ na_nx^{n−1}+x^2 \sum_{n=0}^∞ a_nx^n&=0 & & \text{Substitution.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+ \sum_{n=0}^∞ a_nx^{n+2}&=0 & & \text{Bring external factors within sums.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Re-index third sum.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+a_1x+\sum_{n=2}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Separate }n=1 \text{ term from second sum.} \\[5pt] a_1x+\sum_{n=2}^∞ [n(n−1)a_n+na_n+a_{n−2}]x^n&=0 & & \text{Collect summation terms.} \\[5pt] a_1x+\sum_{n=2}^∞ [(n^2−n)a_n+na_n+a_{n−2}]x^n &=0 & & \text{Multiply through in first term.} \\[5pt] a_1x+\sum_{n=2}^∞ [n^2a_n+a_{n−2}]x^n &=0. & & \text{Simplify.} \end{align*}\]
Ensuite\(a_1=0\), et pour\(n≥2,\)
\[\begin{align*} n^2a_n+a_{n−2} &= 0 \\[4pt] a_n&=−\dfrac{1}{n^2}a_{n−2}. \end{align*} \nonumber \]
Parce que\(a_1=0\) tous les termes impairs sont nuls. Ensuite, pour des valeurs égales de\(n,\) nous avons
\[\begin{align*}a_2 &=−\dfrac{1}{2^2}a_0 \\[4pt] a_4 &= −\dfrac{1}{4^2}a_2=\dfrac{1}{4^2⋅2^2} a_0. \\[4pt] a_6 &=−\dfrac{1}{6^2}a_4 =−\dfrac{1}{6^2⋅4^2⋅2^2}a_0 \end{align*}\]
En général,
\[a_{2k}=\dfrac{(−1)^k}{(2)^{2k}(k!)^2}a_0. \nonumber \]
Ainsi, nous avons
\[y(x)=a_0 \sum_{k=0}^∞ \dfrac{(−1)^k}{(2)^{2k}(k!)^2}x^{2k}. \nonumber \]
Le graphique apparaît ci-dessous.
Vérifiez que l'expression trouvée dans Example\(\PageIndex{2}\) est une solution à l'équation de Bessel d'ordre 0.
- Allusion
-
Différenciez la série de puissances terme par terme et remplacez-la dans l'équation différentielle.
Concepts clés
- Les représentations de fonctions en série de puissances peuvent parfois être utilisées pour trouver des solutions à des équations différentielles.
- Différenciez la série de puissance terme par terme et remplacez-la dans l'équation différentielle pour trouver des relations entre les coefficients de la série de puissances.


