Skip to main content
Global

17.3E : Exercices pour la section 17.3

  1. Last updated
  2. Save as PDF
  • Page ID
    197507

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Une masse pesant 4 livres étire un ressort de 8 pouces. Trouvez l'équation du mouvement si le ressort est libéré de la position d'équilibre avec une vitesse descendante de 12 pieds/sec. Quelle est la période et la fréquence du mouvement ?

    2. Une masse pesant 2 livres étire un ressort de 2 pieds. Trouvez l'équation du mouvement si le ressort est relâché à 2 pouces sous la position d'équilibre avec une vitesse ascendante de 8 pieds/sec. Quelle est la période et la fréquence du mouvement ?

    Réponse
    équation différentielle :\(x″+16x=0,\)
    équation du mouvement :\(=\,\frac{π}{2} \text{ sec},\)
    fréquence de\(x(t)=\frac{1}{6} \cos (4t)−2 \sin (4t),\)
    la période\(=\,\frac{2}{π} \text{ Hz}\)

    3. Une masse de 100 g étire un ressort de 0,1 m. Trouvez l'équation du mouvement de la masse si elle est libérée du repos d'une position située à 20 cm en dessous de la position d'équilibre. Quelle est la fréquence de ce mouvement ?

    4. Une masse de 400 g étire un ressort de 5 cm. Trouvez l'équation du mouvement de la masse si elle est libérée du repos à partir d'une position située 15 cm en dessous de la position d'équilibre. Quelle est la fréquence de ce mouvement ?

    Réponse
    équation différentielle :\(x″+196x=0,\)
    équation du mouvement :\(=\,\frac{π}{7} \text{ sec},\)
    fréquence de\(x(t)=0.15 \cos (14t),\)
    la période\(=\,\frac{7}{π} \text{ Hz}\)

    5. Un bloc a une masse de 9 kg et est fixé à un ressort vertical avec une constante de ressort de 0,25 N/m. Le bloc est étiré à 0,75 m en dessous de sa position d'équilibre et relâché.

    1. Trouvez la fonction\(x(t)\) de position du bloc.
    2. Déterminez la période et la fréquence de la vibration.
    3. Esquissez un graphique de\(x(t)\).
    4. À quel moment le bloc passe pour la première fois en position d'équilibre ?

    6. Un bloc a une masse de 5 kg et est fixé à un ressort vertical avec une constante de ressort de 20 N/m. Le bloc est libéré de la position d'équilibre à une vitesse descendante de 10 m/sec.

    1. Trouvez la fonction\(x(t)\) de position du bloc.
    2. Déterminez la période et la fréquence de la vibration.
    3. Esquissez un graphique de\(x(t)\).
    4. À quel moment le bloc passe pour la première fois en position d'équilibre ?
    Réponse

    a.\(x(t)=5 \sin (2t)\)
    b.\(=π \text{ sec},\)
    fréquence de la période\(=\frac{1}{π} \text{ Hz}\)
    c.
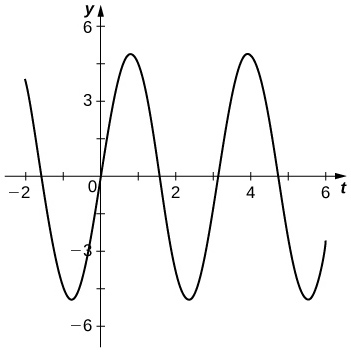
    Cette figure est le graphique d'une fonction. Il s'agit d'une fonction périodique avec une amplitude constante. L'axe horizontal est étiqueté par incréments de 1. L'axe vertical est étiqueté par incréments de 1,5.
    d.\(t=\frac{π}{2} \text{ sec}\)

    7. Une masse de 1 kg est fixée à un ressort vertical avec une constante de ressort de 21 N/m. La résistance dans le système masse-ressort est égale à 10 fois la vitesse instantanée de la masse.

    1. Déterminez l'équation du mouvement si la masse est libérée d'une position située à 2 m en dessous de sa position d'équilibre avec une vitesse descendante de 2 m/sec.
    2. Représentez graphiquement la solution et déterminez si le mouvement est suramorti, amorti de manière critique ou sous-amortie.

    8. Un poids de 800 livres (25 limaces) est fixé à un ressort vertical avec une constante de ressort de 226 lb/pi. Le système est immergé dans un milieu qui confère une force d'amortissement égale à 10 fois la vitesse instantanée de la masse.

    1. Trouvez l'équation du mouvement s'il est relâché d'une position située à 20 pieds en dessous de sa position d'équilibre avec une vitesse descendante de 41 pieds/sec.
    2. Représentez graphiquement la solution et déterminez si le mouvement est suramorti, amorti de manière critique ou sous-amortie.
    Réponse

    un.\(x(t)=e^{−t/5}(20 \cos (3t)+15 \sin(3t))\)

    b. sous-amorti

    9. Une masse de 9 kg est fixée à un ressort vertical avec une constante de ressort de 16 N/m. Le système est immergé dans un milieu qui confère une force d'amortissement égale à 24 fois la vitesse instantanée de la masse.

    1. Trouvez l'équation du mouvement s'il est libéré de sa position d'équilibre avec une vitesse ascendante de 4 m/sec.
    2. Représentez graphiquement la solution et déterminez si le mouvement est suramorti, amorti de manière critique ou sous-amortie.

    10. Une masse de 1 kg étire un ressort de 6,25 cm. La résistance dans le système masse-ressort est égale à huit fois la vitesse instantanée de la masse.

    1. Déterminez l'équation du mouvement si la masse est libérée d'une position située 5 m en dessous de sa position d'équilibre avec une vitesse ascendante de 10 m/sec.
    2. Déterminez si le mouvement est suramorti, amorti de manière critique ou sous-amortie.
    Réponse

    un.\(x(t)=5e^{−4t}+10te^{−4t}\)

    b. fortement amorti

    11. Un poids de 32 livres (1 limace) étire un ressort vertical de 4 po. La résistance dans le système masse-ressort est égale à quatre fois la vitesse instantanée de la masse.

    1. Trouvez l'équation du mouvement s'il est libéré de sa position d'équilibre avec une vitesse descendante de 12 pieds/sec.
    2. Déterminez si le mouvement est suramorti, amorti de manière critique ou sous-amortie.

    12. Un poids de 64 livres est fixé à un ressort vertical avec une constante de ressort de 4,625 lb/pi. La résistance dans le système masse-ressort est égale à la vitesse instantanée. Le poids est mis en mouvement à partir d'une position située à 1 pied en dessous de sa position d'équilibre avec une vitesse ascendante de 2 pieds/sec. La masse est-elle au-dessus ou en dessous de la position de l'équation à la fin de la\(π\) seconde ? À quelle distance ?

    Réponse
    \(x(π)=\frac{7e^{−π/4}}{6}\)pieds en dessous

    13. Une masse qui pèse 8 livres étire un ressort de 6 pouces. Le système est soumis à une force externe de\(8 \sin 8t \) lb. Si la masse est abaissée de 3 pouces puis relâchée, déterminez la position de la masse à tout moment.

    14. Une masse qui pèse 6 livres étire un ressort de 3 pouces. Le système est soumis à une force externe de\(8 \sin (4t) \) lb. Si la masse est abaissée de 1 pouce puis relâchée, déterminez la position de la masse à tout moment.

    Réponse
    \(x(t)=\frac{32}{9} \sin (4t)+ \cos (\sqrt{128}t)−\frac{16}{9\sqrt{2}} \sin (\sqrt{128}t)\)

    15. Trouvez la charge du condensateur dans un circuit de la série RLC où\(L=40\) H\(R=30\,Ω\),\(C=1/200\) F et\(E(t)=200\) V. Supposons que la charge initiale du condensateur est de 7 C et que le courant initial est de 0 A.

    16. Trouvez la charge du condensateur dans un circuit de la série RLC où\(L=2\) H,\(R=24\,Ω,\)\(C=0.005\) F et\(E(t)=12 \sin 10t\) V. Supposons que la charge initiale du condensateur est de 0,001 C et que le courant initial est de 0 A.

    Réponse
    \(q(t)=e^{−6t}(0.051 \cos (8t)+0.03825 \sin (8t))−\frac{1}{20} \cos (10t)\)

    17. Un circuit en série consiste en un dispositif où\(L=1\) H,\(R=20\,Ω,\)\(C=0.002\) F et\(E(t)=12\) V. Si la charge et le courant initiaux sont tous deux nuls, trouvez la charge et le courant à la fois\(t.\)

    18. Un circuit en série consiste en un dispositif où\(L=12\) H\(R=10\,Ω\),\(C=\frac{1}{50}\) F et\(E(t)=250\) V. Si la charge initiale du condensateur est de 0 C et que le courant initial est de 18 A, trouvez la charge et le courant à la fois\(t.\)

    Réponse
    \(q(t)=e^{−10t}(−32t−5)+5,I(t)=2e^{−10t}(160t+9)\)