17.3 : Applications des équations différentielles du second ordre
- Page ID
- 197497
- Résolvez une équation différentielle du second ordre représentant un mouvement harmonique simple.
- Résolvez une équation différentielle du second ordre représentant un mouvement harmonique simple amorti.
- Résolvez une équation différentielle du second ordre représentant un mouvement harmonique simple forcé.
- Résolvez une équation différentielle du second ordre représentant la charge et le courant dans un circuit de la série RLC.
Nous avons vu dans l'introduction du chapitre que les équations différentielles linéaires du second ordre sont utilisées pour modéliser de nombreuses situations en physique et en ingénierie. Dans cette section, nous verrons comment cela fonctionne pour les systèmes composés d'un objet dont la masse est fixée à un ressort vertical et d'un circuit électrique contenant une résistance, une inductance et un condensateur connectés en série. De tels modèles peuvent être utilisés pour approximer d'autres situations plus complexes ; par exemple, les liaisons entre des atomes ou des molécules sont souvent modélisées comme des ressorts qui vibrent, comme le décrivent ces mêmes équations différentielles.
Mouvement harmonique simple
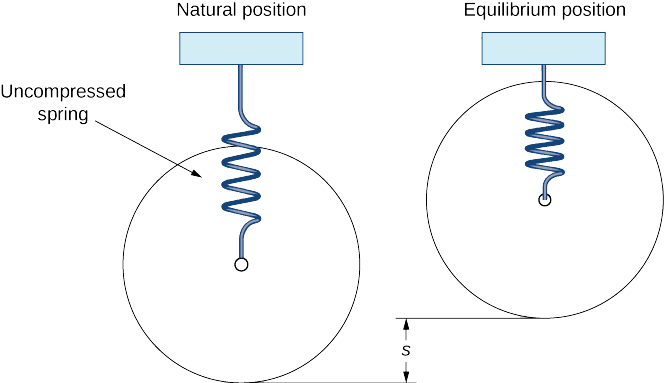
Prenons l'exemple d'une masse suspendue à un ressort fixé à un support rigide. (C'est ce que l'on appelle communément un système de masse à ressort.) La gravité tire la masse vers le bas et la force de rappel du ressort tire la masse vers le haut. Comme le montre la figure\(\PageIndex{1}\), lorsque ces deux forces sont égales, on dit que la masse est en position d'équilibre. Si la masse est déplacée par rapport à l'équilibre, elle oscille de haut en bas. Ce comportement peut être modélisé par une équation différentielle à coefficient constant du second ordre.
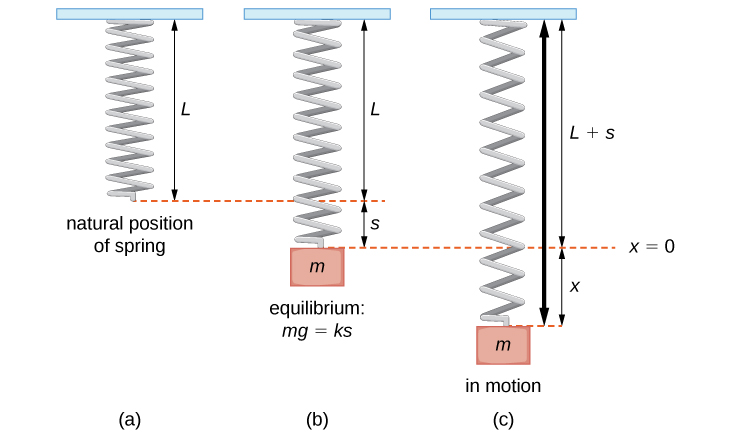
\(x(t)\)Dénotons le déplacement de la masse par rapport à l'équilibre. Notez que pour les systèmes à masse à ressort de ce type, il est habituel d'adopter la convention selon laquelle le duvet est positif. Ainsi, un déplacement positif indique que la masse est en dessous du point d'équilibre, alors qu'un déplacement négatif indique que la masse est au-dessus de l'équilibre. Le déplacement est généralement exprimé en pieds dans le système anglais ou en mètres dans le système métrique.
Considérez les forces qui agissent sur la masse. La force de gravité est donnée par mg.mg. Dans le système anglais, la masse est exprimée en limaces et l'accélération résultant de la gravité est exprimée en pieds par seconde au carré. L'accélération résultant de la gravité est constante, donc dans le système anglais,\(g=32\, ft/sec^2\). Rappelez-vous que 1 pied de limace par seconde 2 correspond à une livre, donc l'expression mg peut être exprimée en livres. Les unités du système métrique sont le kilogramme pour la masse et le m/sec 2 pour l'accélération gravitationnelle. Dans le système métrique, nous avons\(g=9.8\) m/sec 2.
Selon la loi de Hooke, la force de rappel du ressort est proportionnelle au déplacement et agit dans la direction opposée au déplacement. La force de rappel est donc donnée par\(−k(s+x).\) La constante du ressort est donnée en livres par pied dans le système anglais et en newtons par mètre en le système métrique.
Maintenant, selon la deuxième loi de Newton, la somme des forces sur le système (gravité plus force de rappel) est égale à la masse multipliée par l'accélération, donc nous avons
\[\begin{align*}mx″ &=−k(s+x)+mg \\[4pt] &=−ks−kx+mg. \end{align*}\]
Cependant, d'après la façon dont nous avons défini notre position d'équilibre\(mg=ks\), l'équation différentielle devient
\[mx″+kx=0. \nonumber \]
Il est pratique de réorganiser cette équation et d'introduire une nouvelle variable, appelée fréquence angulaire\(ω\). \(ω=\sqrt{k/m}\)En laissant, nous pouvons écrire l'équation comme
\[x''+ω^2x=0. \nonumber \]
Cette équation différentielle a la solution générale
\[x(t)=c_1 \cos ωt+c_2 \sin ωt, \label{GeneralSol} \]
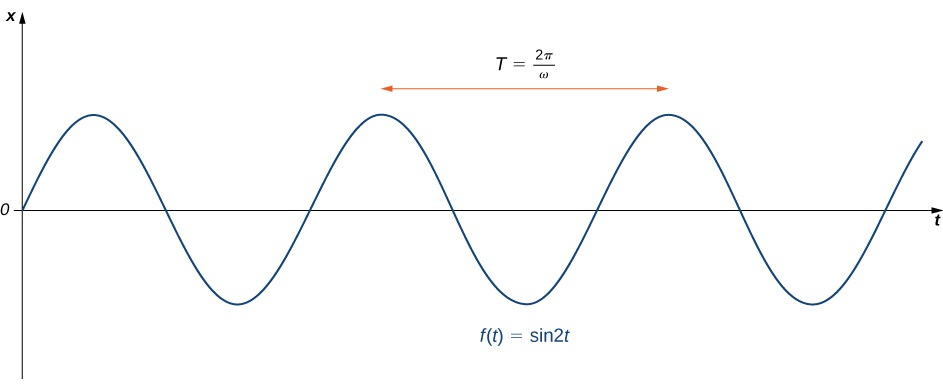
qui donne la position de la masse à tout moment. Le mouvement de la masse est appelé mouvement harmonique simple. La période de ce mouvement (le temps nécessaire pour terminer une oscillation) est\(T=\dfrac{2π}{ω}\) et la fréquence est\(f=\dfrac{1}{T}=\dfrac{ω}{2π}\) (Figure\(\PageIndex{2}\)).
Supposons qu'un objet pesant 2 livres étire un ressort de 6 pouces. Trouvez l'équation du mouvement si le ressort est libéré de la position d'équilibre avec une vitesse ascendante de 16 pieds/sec. Quelle est la durée de la motion ?
Solution
Nous devons d'abord trouver la constante du ressort. Nous avons
\[\begin{align*}mg &=ks\\[4pt] 2 &=k \left(\dfrac{1}{2}\right)\\[4pt] k &=4. \end{align*}\]
Nous savons également que le poids\(W\) est égal au produit de la masse\(m\) et de l'accélération due à la gravité\(g\). En unités anglaises, l'accélération due à la gravité est de 32 pieds/sec 2.
\[\begin{align*}W &=mg\\[4pt] 2 &=m(32)\\[4pt] m &=\dfrac{1}{16}\end{align*}\]
Ainsi, l'équation différentielle représentant ce système est
\[\dfrac{1}{16}x″+4x=0. \nonumber \]
En multipliant par 16, nous obtenons\(x''+64x=0,\) ce qui peut également être écrit sous la forme\(x''+(8^2)x=0.\) Cette équation a la solution générale
\[x(t)=c_1 \cos (8t)+c_2 \sin (8t). \nonumber \]
La masse a été libérée de la position d'équilibre, donc\(x(0)=0\), et elle avait une vitesse ascendante initiale de 16 pieds/sec, donc\(x′(0)=−16\). L'application de ces conditions initiales pour résoudre\(c_1\) et\(c_2\)... donne
\[x(t)=−2 \sin 8t. \nonumber \]
La durée de ce mouvement est de 2\(\dfrac{2π}{8}=\dfrac{π}{4}\) secondes.
Une masse de 200 g étire un ressort de 5 cm. Trouvez l'équation du mouvement de la masse si elle est libérée du repos à partir d'une position située 10 cm en dessous de la position d'équilibre. Quelle est la fréquence de ce mouvement ?
- Allusion
-
Trouvez d'abord la constante du ressort.
- Réponse
-
\(x(t)=0.1 \cos (14t)\)(en mètres) ; la fréquence est\(\dfrac{14}{2π}\) Hz.
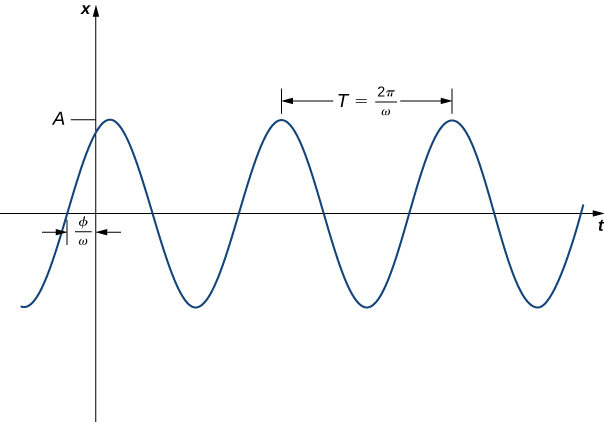
L'écriture de la solution générale sous la forme\(x(t)=c_1 \cos (ωt)+c_2 \sin(ωt)\) (Equation \ ref {GeneralSol}) présente certains avantages. Il est facile de voir le lien entre l'équation différentielle et la solution, et la période et la fréquence du mouvement sont évidentes. Cependant, cette forme de fonction nous en dit très peu sur l'amplitude du mouvement. Dans certains cas, il se peut que nous préférions écrire la solution dans le formulaire
\[x(t)=A \sin (ωt+ϕ). \nonumber \]
Bien que le lien avec l'équation différentielle ne soit pas aussi explicite dans ce cas, la période et la fréquence du mouvement sont toujours évidentes. De plus, l'amplitude du mouvement\(A,\) est évidente dans cette forme de fonction. La constante\(ϕ\) est appelée décalage de phase et a pour effet de déplacer le graphe de la fonction vers la gauche ou vers la droite.
Pour convertir la solution sous cette forme, nous voulons trouver les valeurs de\(A\) et\(ϕ\) telles que
\[c_1 \cos (ωt)+c_2 \sin (ωt)=A \sin (ωt+ϕ). \nonumber \]
Nous appliquons d'abord l'identité trigonométrique
\[\sin (α+β)= \sin α \cos β+ \cos α \sin β \nonumber \]
pour obtenir
\[\begin{align*} c_1 \cos (ωt)+c_2 \sin (ωt) &= A( \sin (ωt) \cos ϕ+ \cos (ωt) \sin ϕ) \\[4pt] &= A \sin ϕ( \cos (ωt))+A \cos ϕ( \sin (ωt)). \end{align*}\]
Ainsi,
\[c1=A \sin ϕ \text{ and } c_2=A \cos ϕ. \nonumber \]
Si nous mettons ces deux équations au carré et les additionnons, nous obtenons
\[\begin{align*}c_1^2+c_2^2 &=A^2 \sin _2 ϕ+A^2 \cos _2 ϕ \\[4pt] &=A^2( \sin ^2 ϕ+ \cos ^2 ϕ) \\[4pt] &=A^2. \end{align*}\]
Ainsi,
\[A=\sqrt{c_1^2+c_2^2}. \nonumber \]
Maintenant, pour trouver\(ϕ\), revenez aux équations pour\(c_1\) et\(c_2\), mais cette fois, divisez la première équation par la deuxième équation pour obtenir
\[\begin{align*} \dfrac{c_1}{c_2} &=\dfrac{A \sin ϕ}{A \cos ϕ} \\[4pt] &= \tan ϕ. \end{align*} \nonumber \]
Ensuite,
\[\tan ϕ= \dfrac{c_1}{c_2}. \nonumber \]
Nous résumons cette constatation dans le théorème suivant.
La fonction\(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\) peut être écrite sous la forme\(x(t)=A \sin (ωt+ϕ)\), où\(A=\sqrt{c_1^2+c_2^2}\) et\( \tan ϕ = \dfrac{c_1}{c_2}\).
Notez que lorsque vous utilisez la formule\( \tan ϕ=\dfrac{c_1}{c_2}\) pour trouver\(ϕ\), nous devons veiller à ce qu'elle\(ϕ\) se trouve dans le bon quadrant (Figure\(\PageIndex{3}\)).
Exprimez les fonctions suivantes dans le formulaire\(A \sin (ωt+ϕ) \). Quelle est la fréquence des mouvements ? L'amplitude ?
- \(x(t)=2 \cos (3t)+ \sin (3t)\)
- \(x(t)=3 \cos (2t)−2 \sin (2t)\)
Solution
Nous avons
\[A=\sqrt{c_1^2+c_2^2}=\sqrt{2^2+1^2}=\sqrt{5} \nonumber \]
et
\[ \tan ϕ = \dfrac{c_1}{c_2}=\dfrac{2}{1}=2. \nonumber \]
Notez que\(c_1\) les deux\(c_2\) sont positifs, il en\(ϕ\) va de même pour le premier quadrant. Ainsi,
\[ϕ≈1.107 \; \text{rad}, \nonumber \]
nous avons donc
\[ x(t) = 2 \cos (3t)+ \sin (3t) =5 \sin (3t+1.107). \nonumber \]
La fréquence est\(\dfrac{ω}{2π}=\dfrac{3}{2π}≈0.477.\) L'amplitude est\(\sqrt{5}\).
- Nous avons
\[A=\sqrt{c_1^2+c_2^2}=\sqrt{3^2+2^2}=\sqrt{13} \nonumber \]
et\[ \tan ϕ = \dfrac{c_1}{c_2}= \dfrac{3}{−2}=−\dfrac{3}{2}. \nonumber \]
Notez que\(c_1\) c'est positif mais\(c_2\) négatif, de même\(ϕ\) que dans le quatrième quadrant. Ainsi,\[ϕ≈−0.983 \; \text{rad}, \nonumber \]
nous avons donc\[\begin{align*} x(t) &=3 \cos (2t) −2 \sin (2t) \\ &= \sqrt{13} \sin (2t−0.983). \end{align*}\]
La fréquence est\(\dfrac{ω}{2π}=\dfrac{2}{2π}≈0.318.\) L'amplitude est\(\sqrt{13}\).
Exprimez la fonction\(x(t)= \cos (4t) + 4 \sin (4t)\) dans le formulaire\(A \sin (ωt+ϕ) \). Quelle est la fréquence des mouvements ? L'amplitude ?
- Allusion
-
Utilisez le processus décrit dans l'exemple\(\PageIndex{2}\).
- Réponse
-
\(x(t)= \sqrt{17} \sin (4t+0.245), \text{frequency} =\dfrac{4}{2π}≈0.637, A=\sqrt{17}\)
Vibrations amorties
Avec le modèle qui vient d'être décrit, le mouvement de la masse se poursuit indéfiniment. De toute évidence, cela ne se produit pas dans le monde réel. Dans le monde réel, il y a presque toujours une certaine friction dans le système, ce qui fait que les oscillations s'éteignent lentement, un effet appelé amortissement. Voyons maintenant comment intégrer cette force d'amortissement dans notre équation différentielle.
Les systèmes physiques à masse à ressort présentent presque toujours un certain amortissement dû à la friction, à la résistance à l'air ou à un amortisseur physique, appelé pot de bord (vérin pneumatique ; Figure\(\PageIndex{4}\)).
Comme l'amortissement est avant tout une force de friction, nous supposons qu'il est proportionnel à la vitesse de la masse et agit dans la direction opposée. La force d'amortissement est donc donnée par\(−bx′\) une constante\(b>0\). Toujours en appliquant la deuxième loi de Newton, l'équation différentielle devient
\[mx″+bx′+kx=0. \nonumber \]
Ensuite, l'équation caractéristique associée est
\[mλ^2+bλ+k=0. \nonumber \]
En appliquant la formule quadratique, nous avons
\[λ=\dfrac{−b±\sqrt{b^2−4mk}}{2m}. \nonumber \]
Tout comme dans les équations linéaires du second ordre, nous considérons trois cas, selon que l'équation caractéristique possède des racines réelles distinctes, une racine réelle répétée ou des racines conjuguées complexes.
Cas 1 : Vibrations suramorties
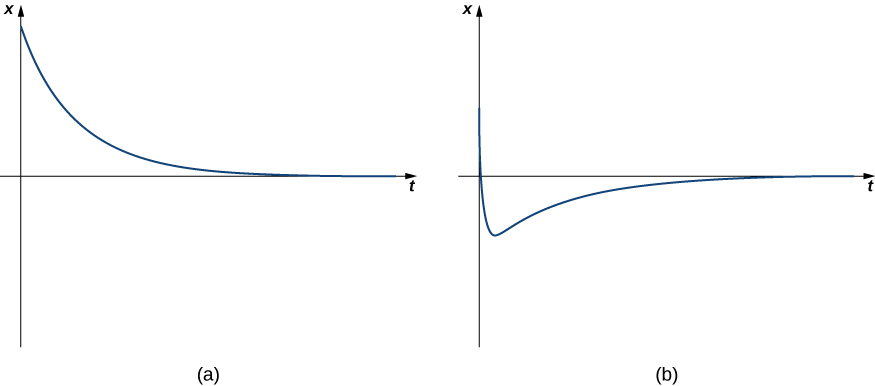
Quand\(b^2>4mk\), on dit que le système est suramorti. La solution générale a la forme
\[x(t)=c_1e^{λ_1t}+c_2e^{λ_2t}, \nonumber \]
où les deux\(λ_1\) et\(λ_2\) sont inférieurs à zéro. Comme les exposants sont négatifs, le déplacement diminue jusqu'à zéro au fil du temps, généralement assez rapidement. Les systèmes suramortis n'oscillent pas (pas plus d'un changement de direction), mais reviennent simplement vers la position d'équilibre. La figure\(\PageIndex{5}\) montre à quoi ressemble un comportement typique avec amortissement critique.
Une masse de 16 livres est fixée à un ressort de 10 pieds. Lorsque la masse s'arrête en position d'équilibre, le ressort mesure 15 pieds 4 pouces. Le système est immergé dans un milieu qui confère une force d'amortissement égale à 5252 fois la vitesse instantanée de la masse. Trouvez l'équation du mouvement si la masse est poussée vers le haut à partir de la position d'équilibre avec une vitesse ascendante initiale de 5 pieds/sec. Quelle est la position de la masse après 10 secondes ? Sa vélocité ?
Solution
La masse étire le ressort de 5 pieds 4 pouces, ou\(\dfrac{16}{3}\) pieds. \(16=\left(\dfrac{16}{3}\right)k,\)Ainsi,\(k=3.\) nous avons également\(m=\dfrac{16}{32}=\dfrac{1}{2}\), donc l'équation différentielle est
\[\dfrac{5}{2}x′+3x=0. \nonumber \]
En multipliant par 2\(x″+5x′+6x=0\), on obtient la solution générale
\[x(t)=c_1e^{−2t}+c_2e^{−3t}. \nonumber \]
En appliquant les conditions initiales\(x′(0)=−5\),\(x(0)=0\) et nous obtenons
\[x(t)=−5e^{−2t}+5e^{−3t}. \nonumber \]
Après 10 secondes, la masse est en position
\[x(10)=−5e^{−20}+5e^{−30}≈−1.0305×10^{−8}≈0, \nonumber \]
il est donc, en fait, en position d'équilibre. Nous l'avons fait\(x′(t)=10e^{−2t}−15e^{−3t}\), donc après 10 secondes, la masse se déplace à une vitesse de
\[x′(10)=10e^{−20}−15e^{−30}≈2.061×10^{−8}≈0. \nonumber \]
Après seulement 10 secondes, la masse bouge à peine.
Une masse de 2 kg est fixée à un ressort avec une constante de ressort de 24 N/m. Le système est ensuite immergé dans un milieu conférant une force d'amortissement égale à 16 fois la vitesse instantanée de la masse. Déterminez l'équation du mouvement s'il est libéré du repos à un point situé à 40 cm en dessous de l'équilibre.
- Allusion
-
Suivez le processus de l'exemple précédent.
- Réponse
-
\(x(t)=0.6e^{−2t}−0.2e^{−6t}\)
Cas 2 : Vibrations fortement amorties
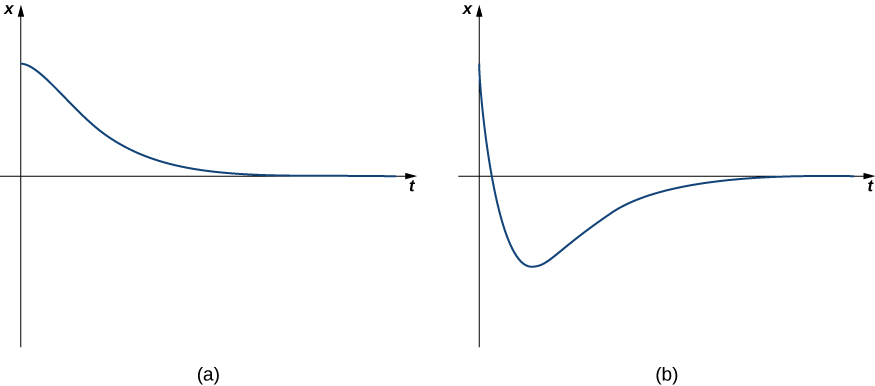
Quand\(b^2=4mk\), nous disons que le système est soumis à un amortissement critique. La solution générale a la forme
\[x(t)=c_1e^{λ_1t}+c_2te^{λ_1t}, \nonumber \]
où\(λ_1\) est inférieur à zéro. Le mouvement d'un système à amortissement critique est très similaire à celui d'un système suramorti. Elle n'oscille pas. Cependant, avec un système à amortissement critique, si l'amortissement est réduit ne serait-ce que légèrement, il en résulte un comportement oscillatoire. D'un point de vue pratique, les systèmes physiques sont presque toujours soit suramortis soit sous-amortis (cas 3, que nous examinons ensuite). Il est impossible d'affiner les caractéristiques d'un système physique de telle sorte qu'\(b^2\)\(4mk\)elles soient exactement égales. La figure\(\PageIndex{6}\) montre à quoi ressemble un comportement typique avec amortissement critique.
Une masse de 1 kg étire un ressort de 20 cm. Le système est fixé à un tableau de bord qui confère une force d'amortissement égale à 14 fois la vitesse instantanée de la masse. Trouvez l'équation du mouvement si la masse est libérée de l'équilibre avec une vitesse ascendante de 3 m/sec.
Solution
Nous avons donc\(mg=1(9.8)=0.2k\),\(k=49.\) alors, l'équation différentielle est
\[x″+14x′+49x=0, \nonumber \]
qui a une solution générale
\[x(t)=c_1e^{−7t}+c_2te^{−7t}. \nonumber \]
L'application des conditions initiales\(x(0)=0\) et\(x′(0)=−3\) donne
\[x(t)=−3te^{−7t}. \nonumber \]
Un poids de 1 livre étire un ressort de 6 pouces, et le système est fixé à un tableau de bord qui confère une force d'amortissement égale à la moitié de la vitesse instantanée de la masse. Déterminez l'équation du mouvement si la masse est libérée du repos à un point situé à 6 pouces sous l'équilibre.
- Allusion
-
Trouvez d'abord la constante du ressort.
- Réponse
-
\(x(t)=\dfrac{1}{2}e^{−8t}+4te^{−8t} \)
Cas 3 : Vibrations non amorties
Quand\(b^2<4mk\), on dit que le système est sous-amorti. La solution générale a la forme
\[x(t)=e^{αt}(c_1 \cos (βt) + c_2 \sin (βt)), \nonumber \]
où\(α\) est inférieur à zéro. Les systèmes sous-amortis oscillent en raison des termes sinus et cosinus de la solution. Cependant, le terme exponentiel finit par dominer, de sorte que l'amplitude des oscillations diminue avec le temps. La figure\(\PageIndex{7}\) montre à quoi ressemble un comportement sous-amorti typique.
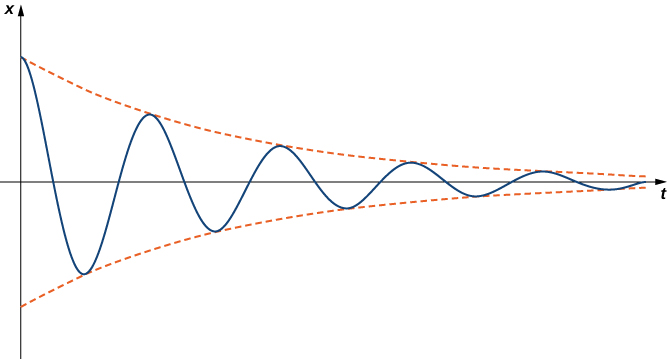
Notez que pour tous les systèmes amortis,\( \lim \limits_{t \to \infty} x(t)=0\). Le système se rapproche toujours de la position d'équilibre au fil du temps.
Un poids de 16 livres étire un ressort de 3,2 pieds. Supposons que la force d'amortissement sur le système est égale à la vitesse instantanée de la masse. Déterminez l'équation du mouvement si la masse est libérée du repos à un point situé à 9 pouces sous l'équilibre.
Solution
Nous l'avons fait\(k=\dfrac{16}{3.2}=5\) et\(m=\dfrac{16}{32}=\dfrac{1}{2},\) donc l'équation différentielle est
\[\dfrac{1}{2} x″+x′+5x=0, \; \text{or} \; x″+2x′+10x=0. \nonumber \]
Cette équation a la solution générale
\[x(t)=e^{−t} ( c_1 \cos (3t)+c_2 \sin (3t) ) . \nonumber \]
En appliquant les conditions initiales,\(x(0)=\dfrac{3}{4}\) et\(x′(0)=0,\) nous obtenons
\[x(t)=e^{−t} \bigg( \dfrac{3}{4} \cos (3t)+ \dfrac{1}{4} \sin (3t) \bigg) . \nonumber \]
Une masse de 1 kg étire un ressort de 49 cm. Le système est immergé dans un milieu qui confère une force d'amortissement égale à quatre fois la vitesse instantanée de la masse. Déterminez l'équation du mouvement si la masse est libérée du repos à un point situé à 24 cm au-dessus de l'équilibre.
- Allusion
-
Trouvez d'abord la constante du ressort.
- Réponse
-
\(x(t)=−0.24e^{−2t} \cos (4t)−0.12e^{−2t} \sin (4t) \)
Pour les pilotes de motocross, les systèmes de suspension de leurs motos sont très importants. Les parcours tout-terrain qu'ils empruntent comportent souvent des sauts, et perdre le contrôle de la moto à l'atterrissage peut leur coûter la course.

Ce système de suspension peut être modélisé comme un système de masse à ressort amorti. Nous définissons notre cadre de référence par rapport au cadre de la moto. Supposons que l'extrémité de l'amortisseur fixé au cadre de la moto soit fixe. Ensuite, la « masse » de notre système de masse à ressort est la roue de la moto. Nous mesurons la position de la roue par rapport au cadre de la moto. Cela peut sembler contre-intuitif, puisque, dans de nombreux cas, c'est en fait le châssis de la moto qui se déplace, mais ce cadre de référence préserve le développement de l'équation différentielle qui a été fait précédemment. Comme pour les développements précédents, nous définissons la direction descendante comme étant positive.
Lorsque la moto est soulevée par son châssis, la roue est suspendue librement et le ressort n'est pas comprimé. Il s'agit de la position naturelle du ressort. Lorsque la moto est posée au sol et que le conducteur la monte, le ressort se comprime et le système est en position d'équilibre (Figure\(\PageIndex{9}\)).
Ce système peut être modélisé à l'aide de la même équation différentielle que nous avons utilisée auparavant :
\[mx″+bx′+kx=0. \nonumber \]
Une motocyclette de motocross pèse 204 livres, et nous supposons que le poids du pilote est de 180 livres. Lorsque le pilote monte la moto, la suspension se comprime de 4 pouces, puis s'arrête à l'équilibre. Le système de suspension fournit un amortissement égal à 240 fois la vitesse verticale instantanée de la moto (et du pilote).
- Définissez l'équation différentielle qui modélise le comportement du système de suspension de la moto.
- Nous nous intéressons à ce qui se passe lorsque la moto atterrit après un saut. Soit le temps\[t=0 \nonumber \] le moment où la moto entre en contact avec le sol pour la première fois. Si la moto heurte le sol à une vitesse de 10 pieds/sec vers le bas, trouvez l'équation du mouvement de la moto après le saut.
- Représentez graphiquement l'équation du mouvement pendant la première seconde après que la moto a heurté le sol.
Solution
- Nous avons défini l'équilibre comme étant le point où\(mg=ks\), donc, nous avons
\[\begin{align*} mg &=ks \\ 384 &=k\left(\dfrac{1}{3}\right)\\ k &=1152. \end{align*}\]
Nous avons également
\[\begin{align*} W &=mg \\ 384 &=m(32) \\ m &=12. \end{align*}\]
Par conséquent, l'équation différentielle qui modélise le comportement de la suspension de la moto est
\[12x″+240x′+1152x=0. \nonumber \]
En divisant par 12, on obtient
\[x''+20x′+96x=0. \nonumber \]
- L'équation différentielle trouvée dans la partie a. a la solution générale
\[x(t)=c_1e^{−8t}+c_2e^{−12t}. \nonumber \]
Maintenant, pour déterminer nos conditions initiales, nous prenons en compte la position et la vitesse de la roue de la moto lorsque celle-ci entre en contact pour la première fois avec le sol. Comme la motocyclette était en l'air avant d'entrer en contact avec le sol, la roue était suspendue librement et le ressort n'était pas comprimé. La roue mesure donc 4 pouces. \(\left(\dfrac{1}{3}\text{ ft}\right)\)en dessous de la position d'équilibre (par rapport au cadre de la moto), et nous avons\(x(0)=\dfrac{1}{3}.\) Selon l'énoncé du problème, la moto a une vitesse de 10 pieds/sec vers le bas lorsque la moto entre en contact avec le sol, donc en\(x′(0)=10.\) appliquant ces conditions initiales, nous obtenons\(c_1=\dfrac{7}{2}\) et \(c_2=−\left(\dfrac{19}{6}\right)\), donc l'équation du mouvement est
\[x(t)=\dfrac{7}{2}e^{−8t}−\dfrac{19}{6}e^{−12t}. \nonumber \]
- Le graphique est illustré dans la figure\(\PageIndex{10}\).

La NASA prépare une mission sur Mars. Pour économiser de l'argent, les ingénieurs ont décidé d'adapter l'un des véhicules d'atterrissage sur la lune pour la nouvelle mission. Cependant, ils s'inquiètent de la façon dont les différentes forces gravitationnelles affecteront le système de suspension qui amortit l'engin lorsqu'il touche le sol. L'accélération due à la gravité sur la Lune est de 1,6 m/sec 2, alors que sur Mars, elle est de 3,7 m/sec 2.
Le système de suspension de l'engin peut être modélisé comme un système de masse à ressort amorti. Dans ce cas, le ressort se trouve sous l'atterrisseur lunaire, de sorte que le ressort est légèrement comprimé à l'équilibre, comme le montre la figure\(\PageIndex{11}\).
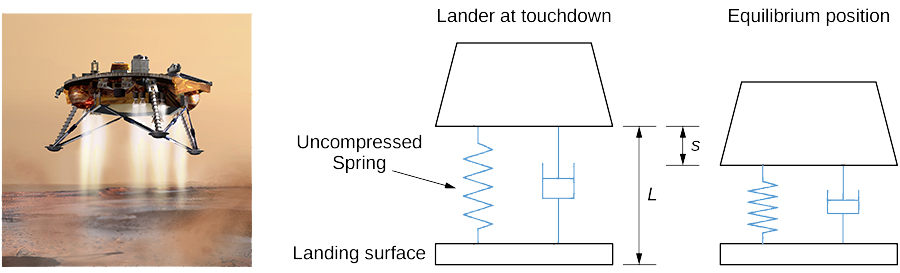
Nous maintenons la convention selon laquelle une baisse est positive. Malgré la nouvelle orientation, l'examen des forces affectant l'atterrisseur montre que la même équation différentielle peut être utilisée pour modéliser la position de l'engin de débarquement par rapport à l'équilibre :
\[mx''+bx′+kx=0, \nonumber \]
où\(m\) est la masse de l'atterrisseur,\(b\) le coefficient d'amortissement et\(k\) la constante du ressort.
- L'atterrisseur a une masse de 15 000 kg et le ressort mesure 2 m de long lorsqu'il n'est pas comprimé. L'atterrisseur est conçu pour comprimer le ressort de 0,5 m afin d'atteindre la position d'équilibre sous la gravité lunaire. Le tableau de bord confère une force d'amortissement égale à 48 000 fois la vitesse instantanée de l'atterrisseur. Définissez l'équation différentielle qui modélise le mouvement de l'atterrisseur lorsque l'engin atterrit sur la lune.
- Supposons que le\(t=0\) temps indique l'instant où l'atterrisseur se pose. La vitesse de descente de l'atterrisseur peut être contrôlée par l'équipage, de sorte qu'il descend à une vitesse de 2 m/sec lorsqu'il touche le sol. Trouvez l'équation du mouvement de l'atterrisseur sur la lune.
- Si l'atterrisseur se déplace trop vite lorsqu'il touche le sol, il peut comprimer complètement le ressort et « du bas vers l'extérieur ». Le creusement du sol pourrait endommager l'embarcation de débarquement et doit être évité à tout prix. Représentez graphiquement l'équation du mouvement trouvée dans la partie 2. Si le ressort mesure 0,5 m de long lorsqu'il est complètement comprimé, l'atterrisseur risque-t-il de tomber au fond ?
- En supposant que les ingénieurs de la NASA n'ajustent ni le ressort ni l'amortisseur, dans quelle mesure l'atterrisseur comprime-t-il le ressort pour atteindre la position d'équilibre sous la gravité martienne ?
- Si l'équipage de l'atterrisseur utilise les mêmes procédures sur Mars que sur la Lune et maintient le taux de descente à 2 m/sec, l'atterrisseur va-t-il atteindre le fond lorsqu'il atterrira sur Mars ?
- Quels ajustements, le cas échéant, les ingénieurs de la NASA devraient-ils apporter pour utiliser l'atterrisseur en toute sécurité sur Mars ?
Vibrations forcées
Le dernier cas que nous considérons est celui où une force extérieure agit sur le système. Dans le cas du système de suspension de la moto, par exemple, les bosses de la route agissent comme une force externe agissant sur le système. Un autre exemple est celui d'un ressort suspendu à un support ; si le support est mis en mouvement, ce mouvement sera considéré comme une force externe exercée sur le système. Nous modélisons ces systèmes forcés à l'aide de l'équation différentielle non homogène
\[mx″+bx′+kx=f(t), \nonumber \]
où la force externe est représentée par le\(f(t)\) terme. Comme nous l'avons vu dans les équations linéaires non homogènes, les équations différentielles de ce type ont des solutions de la forme
\[x(t)=c_1x_1(t)+c_2x_2(t)+x_p(t), \nonumber \]
où\(c_1x_1(t)+c_2x_2(t)\) est la solution générale à l'équation complémentaire et\(x_p(t)\) est une solution particulière à l'équation non homogène. Si le système est amorti,\(\lim \limits_{t \to \infty} c_1x_1(t)+c_2x_2(t)=0.\) puisque ces termes n'affectent pas le comportement à long terme du système, nous appelons cette partie de la solution la solution transitoire. Le comportement à long terme du système est déterminé par\(x_p(t)\), c'est pourquoi nous appelons cette partie de la solution la solution en régime permanent.
Une masse d'une limace étire une source de 2 pieds et vient s'immobiliser en équilibre. Le système est fixé à un tableau de bord qui confère une force d'amortissement égale à huit fois la vitesse instantanée de la masse. Trouvez l'équation du mouvement si une force externe égale à\(f(t)=8 \sin (4t)\) est appliquée au système à partir de l'instant\(t=0\). Qu'est-ce que la solution transitoire ? Qu'est-ce que la solution à l'état d'équilibre ?
Solution
Nous l'avons\(mg=1(32)=2k,\) fait\(k=16\) et l'équation différentielle est
\[x″+8x′+16x=8 \sin (4t). \nonumber \]
La solution générale à l'équation complémentaire est
\[c_1e^{−4t}+c_2te^{−4t}. \nonumber \]
En supposant une solution particulière de la forme\(x_p(t)=A \cos (4t)+ B \sin (4t)\) et en utilisant la méthode des coefficients indéterminés\(x_p (t)=−\dfrac{1}{4} \cos (4t)\), nous trouvons
\[x(t)=c_1e^{−4t}+c_2te^{−4t}−\dfrac{1}{4} \cos (4t). \nonumber \]
\(t=0,\)La masse est au repos dans la position d'équilibre, donc en\(x(0)=x′(0)=0.\) appliquant ces conditions initiales pour résoudre\(c_1\) et\(c_2,\) nous obtenons
\[x(t)=\dfrac{1}{4}e^{−4t}+te^{−4t}−\dfrac{1}{4} \cos (4t). \nonumber \]
La solution transitoire est\(\dfrac{1}{4}e^{−4t}+te^{−4t}\). La solution à l'état d'équilibre est\(−\dfrac{1}{4} \cos (4t).\)
Une masse de 2 kg est fixée à un ressort à 32 N/m constants et s'arrête en position d'équilibre. À partir de ce moment\(t=0\), une force externe égale à\(f(t)=68e^{−2}t \cos (4t) \) est appliquée au système. Trouvez l'équation du mouvement s'il n'y a pas d'amortissement. Qu'est-ce que la solution transitoire ? Qu'est-ce que la solution à l'état d'équilibre ?
- Allusion
-
Trouvez la solution particulière avant d'appliquer les conditions initiales.
- Réponse
-
\(x(t)=−\dfrac{1}{2} \cos (4t)+ \dfrac{9}{4} \sin (4t)+ \dfrac{1}{2} e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)
\(\text{Transient solution:} \dfrac{1}{2}e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)
\(\text{Steady-state solution:} −\dfrac{1}{2} \cos (4t)+ \dfrac{9}{4} \sin (4t) \)
Prenons l'exemple d'un système non amorti présentant un mouvement harmonique simple. Dans le monde réel, nous n'avons jamais vraiment de système non amorti ; il y a toujours un certain amortissement. À des fins théoriques, on pourrait toutefois imaginer un système masse-ressort contenu dans une chambre à vide. En l'absence de résistance à l'air, la masse continuerait de monter et de descendre indéfiniment.
La fréquence du mouvement résultant, donnée par\(f=\dfrac{1}{T}=\dfrac{ω}{2π}\), est appelée fréquence naturelle du système. Si une force externe agissant sur le système a une fréquence proche de la fréquence naturelle du système, il en résulte un phénomène appelé résonance. La force externe renforce et amplifie le mouvement naturel du système.
- Examinez l'équation différentielle\(x″+x=0.\) Trouvez la solution générale. Quelle est la fréquence naturelle du système ?
- Supposons maintenant que ce système soit soumis à une force externe donnée par\(f(t)=5 \cos t.\) Résoudre le problème de la valeur initiale\(x″+x=5 \cos t\),\(x(0)=0\),\(x′(0)=1\).
- Tracez la solution. Qu'advient-il du comportement du système au fil du temps ?
- Dans le monde réel, il y a toujours un certain amortissement. Cependant, si la force d'amortissement est faible et que la force externe est suffisamment forte, les systèmes réels peuvent toujours présenter une résonance. L'un des exemples les plus connus de résonance est l'effondrement du pont Tacoma Narrows le 7 novembre 1940. Le pont avait fait preuve d'un comportement étrange depuis sa construction. La chaussée a connu un étrange « rebond ». Le jour où elle s'est effondrée, une forte tempête de vent a provoqué des torsions et des ondulations violentes de la chaussée. Le pont n'a pas pu résister à ces forces et s'est finalement effondré. Les experts pensent que la tempête a exercé sur le pont des forces très proches de sa fréquence naturelle et que la résonance qui en a résulté a fini par ébranler le pont.
Ce site Web contient plus d'informations sur l'effondrement du pont de Tacoma Narrows.
Pendant la courte période pendant laquelle le pont de Tacoma Narrows a été érigé, il est devenu une attraction touristique. Plusieurs personnes se trouvaient sur place le jour où le pont s'est effondré, et l'une d'elles a filmé l'effondrement.
Regardez la vidéo pour voir l'effondrement du pont « Gallopin' Gertie » de Tacoma Narrows. https://www.youtube.com/watch?v=j-zczJXSxnw
- Un autre exemple concret de résonance est celui d'une chanteuse qui brise un verre à vin en cristal alors qu'elle chante juste la bonne note. Lorsque quelqu'un tape sur un verre à vin en cristal ou mouille un doigt et le passe sur le bord, un ton peut être entendu. Cette note est créée par le verre à vin qui vibre à sa fréquence naturelle. Si un chanteur chante ensuite la même note à un volume suffisamment élevé, le verre se brise à cause de la résonance.
L'émission Mythbusters a diffusé un épisode sur ce phénomène. Visitez ce site Web pour en savoir plus. Adam Savage a également décrit l'expérience. Regardez cette vidéo pour découvrir son compte.
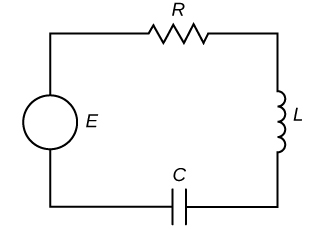
Le circuit de la série RLC
Considérez un circuit électrique contenant une résistance, une bobine d'induction et un condensateur, comme indiqué sur la figure\(\PageIndex{12}\). Un tel circuit est appelé circuit série RLC. Les circuits RLC sont utilisés dans de nombreux systèmes électroniques, notamment comme tuners dans les radios AM/FM. Le bouton de réglage fait varier la capacité du condensateur, qui à son tour règle la radio. De tels circuits peuvent être modélisés par des équations différentielles à coefficient constant du second ordre.
\(I(t)\)Dénotons le courant dans le circuit RLC et\(q(t)\) la charge sur le condensateur. De plus,\(L\) notons l'inductance en henrys (H),\(R\) la résistance en ohms\((Ω)\) et\(C\) la capacité en farads (F). Enfin,\(E(t)\) notons le potentiel électrique en volts (V).
La règle de tension de Kirchhoff stipule que la somme des chutes de tension autour d'une boucle fermée doit être nulle. Nous devons donc prendre en compte les chutes de tension à travers l'inducteur (indiqué\(E_L\)), la résistance (indiqué\(E_R\)) et le condensateur (indiqué\(E_C\)). Comme le circuit RLC illustré sur la figure\(\PageIndex{12}\) comprend une source de tension\(E(t)\), qui ajoute de la tension au circuit, nous avons\(E_L+E_R+E_C=E(t)\).
Nous présentons les formules ci-dessous sans autre développement et ceux d'entre vous qui s'intéressent à la dérivation de ces formules peuvent consulter les liens. En utilisant la loi de Faraday et la loi de Lenz, on peut démontrer que la chute de tension aux bornes d'un inducteur est proportionnelle au taux de variation instantané du courant, avec une constante de proportionnalité.\(L.\) Ainsi,
\[E_L=L\dfrac{dI}{dt}. \nonumber \]
Ensuite, selon la loi d'Ohm, la chute de tension aux bornes d'une résistance est proportionnelle au courant traversant la résistance, avec une constante\(R.\) de proportionnalité.
\[E_R=RI. \nonumber \]
Enfin, la chute de tension aux bornes d'un condensateur est proportionnelle à la charge,\(q,\) sur le condensateur, avec une proportionnalité constante\(1/C\). Ainsi,
\[E_C=\dfrac{1}{C}q. \nonumber \]
En ajoutant ces termes, nous obtenons
\[L\dfrac{dI}{dt}+RI+\dfrac{1}{C}q=E(t). \nonumber \]
En notant que\(I=(dq)/(dt)\), cela devient
\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t). \nonumber \]
Mathématiquement, ce système est analogue aux systèmes de masse à ressort que nous avons examinés dans cette section.
Trouvez la charge du condensateur dans un circuit de la série RLC où\(L=5/3\) H\(R=10Ω\),\(C=1/30\) F et\(E(t)=300\) V. Supposons que la charge initiale du condensateur est de 0 C et que le courant initial est de 9 A. Qu'advient-il de la charge du condensateur au fil du temps ?
Solution
Nous avons
\[\begin{align*} L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q &=E(t) \\[4pt] \dfrac{5}{3} \dfrac{d^2q}{dt^2}+10\dfrac{dq}{dt}+30q &=300 \\[4pt] \dfrac{d^2q}{dt^2}+6\dfrac{dq}{dt}+18q &=180. \end{align*}\]
La solution générale à l'équation complémentaire est
\[e^{−3t}(c_1 \cos (3t)+c_2 \sin (3t)). \nonumber \]
Supposons une solution particulière du formulaire\(q_p=A\), où\(A\) est une constante. En utilisant la méthode des coefficients indéterminés, nous trouvons\(A=10\). Donc,
\[q(t)=e^{−3t}(c_1 \cos (3t)+c_2 \sin (3t))+10. \nonumber \]
En appliquant les conditions initiales\(q(0)=0\) et\(i(0)=((dq)/(dt))(0)=9,\) nous trouvons\(c_1=−10\) et\(c_2=−7.\) donc la charge sur le condensateur est
\[q(t)=−10e^{−3t} \cos (3t)−7e^{−3t} \sin (3t)+10. \nonumber \]
En regardant de plus près cette fonction, nous voyons que les deux premiers termes vont décroître avec le temps (en raison de l'exposant négatif de la fonction exponentielle). Par conséquent, le condensateur se rapproche finalement d'une charge à l'état stable de 10° C.
Trouvez la charge du condensateur dans un circuit de la série RLC où\(L=1/5\) H,\(R=2/5Ω,\)\(C=1/2\) F et\(E(t)=50\) V. Supposons que la charge initiale du condensateur est de 0 C et que le courant initial est de 4 A.
- Allusion
-
N'oubliez pas,\(E_L=L((dI)/(dt)).\)
- Réponse
-
\[q(t)=−25e^{−t} \cos (3t)−7e^{−t} \sin (3t)+25 \nonumber \]
Concepts clés
- Des équations différentielles à coefficient constant du second ordre peuvent être utilisées pour modéliser des systèmes masse-ressort.
- L'examen des forces appliquées à un système masse-ressort donne une équation différentielle de la forme\[mx″+bx′+kx=f(t), \nonumber \] où mm représente la masse, bb est le coefficient de la force d'amortissement,\(k\) est la constante du ressort et\(f(t)\) représente toute force externe nette exercée sur le système.
- Si\(b=0\), aucune force d'amortissement n'agit sur le système, il en résulte un simple mouvement harmonique.
- Si\(b≠0\), le comportement du système dépend\(b^2−4mk>0, b^2−4mk=0,\) du fait que\(b^2−4mk<0.\)
- Si\(b^2−4mk>0,\) le système est suramorti et ne présente pas de comportement oscillatoire.
- Si\(b^2−4mk=0,\) le système est soumis à un amortissement critique. Il ne présente pas de comportement oscillatoire, mais toute légère réduction de l'amortissement se traduirait par un comportement oscillatoire.
- Si\(b^2−4mk<0\), le système est sous-amorti. Il présente un comportement oscillatoire, mais l'amplitude des oscillations diminue avec le temps.
- Si\(f(t)≠0\), la solution de l'équation différentielle est la somme d'une solution transitoire et d'une solution en régime permanent. La solution en régime permanent régit le comportement à long terme du système.
- La charge du condensateur dans un circuit en série RLC peut également être modélisée à l'aide d'une équation différentielle à coefficient constant du second ordre de la forme\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t), \nonumber \] où\(L\)\(R\) est l'inductance,\(C\) la résistance, la capacité et\(E(t)\) la source de tension.
Équations clés
- Équation du mouvement harmonique simple\[x″+ω^2x=0 \nonumber \]
- Solution pour un mouvement harmonique simple\[x(t)=c_1 \cos (ωt)+c_2 \sin (ωt) \nonumber \]
- Autre forme de solution pour SHM\[x(t)=A \sin (ωt+ϕ) \nonumber \]
- Mouvement harmonique forcé\[mx″+bx′+kx=f(t)\nonumber \]
- Recharge dans un circuit de la série RLC\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t),\nonumber \]
Lexique
- Circuit de la série RLC
- un chemin électrique complet composé d'une résistance, d'une inductance et d'un condensateur ; une équation différentielle à coefficient constant du second ordre peut être utilisée pour modéliser la charge sur le condensateur dans un circuit en série RLC
- mouvement harmonique simple
- mouvement décrit par l'équation\(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\), tel que démontré par un système masse-ressort non amorti dans lequel la masse continue d'osciller indéfiniment
- solution à l'état stable
- une solution à une équation différentielle non homogène liée à la fonction de forçage ; à long terme, la solution se rapproche de la solution à l'état d'équilibre


