Skip to main content
Global

16.8E : Exercices pour la section 16.8

  1. Last updated
  2. Save as PDF
  • Page ID
    197816

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pour les exercices 1 à 9, utilisez un système algébrique informatique (CAS) et le théorème de divergence pour évaluer l'intégrale de surface\(\displaystyle \int_S \vecs F \cdot \vecs n \, ds\) pour le choix donné\(\vecs F\) et la surface limite.\(S.\) Pour chaque surface fermée, supposons qu'\(\vecs N\)il s'agit du vecteur normal de l'unité extérieure.

    1. [T]\(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) ;\(S\) est la surface du cube\(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1\).

    2. [T]\(\vecs F(x,y,z) = (\cos yz) \,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + 3z^2 \,\mathbf{\hat k}\) ;\(S\) est la surface de l'hémisphère\(z = \sqrt{4 - x^2 - y^2}\) avec le disque\(x^2 + y^2 \leq 4\) dans le\(xy\) plan.

    Réponse
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 75.3982\)

    3. [T]\(\vecs F(x,y,z) = (x^2 + y^2 - x^2)\,\mathbf{\hat i} + x^2 y\,\mathbf{\hat j} + 3z\,\mathbf{\hat k}; \)\(S\) est la surface des cinq faces du cube unitaire\(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1.\)

    4. [T]\(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}; \)\(S\) est la surface du paraboloïde\(z = x^2 + y^2\) pour\(0 \leq z \leq 9\).

    Réponse
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 127.2345\)

    5. [T]\(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\) ;\(S\) est la surface de la sphère\(x^2 + y^2 + z^2 = 4\).

    6. [T]\(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + (z^2 - 1)\,\mathbf{\hat k}\) ;\(S\) est la surface du solide délimitée par un cylindre\( x^2 + y^2 = 4\) et des plans\(z = 0\) et\(z = 1\).

    Réponse
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 37.699\)

    7. [T]\(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\) ;\(S\) est la surface délimitée en haut par une sphère\(\rho = 2\) et en dessous par un cône\(\varphi = \dfrac{\pi}{4}\) en coordonnées sphériques. (Imaginez-le\(S\) comme la surface d'un « cornet de crème glacée ».)

    8. [T]\(\vecs F(x,y,z) = x^3\,\mathbf{\hat i} + y^3 \,\mathbf{\hat j} + 3a^2z \,\mathbf{\hat k} \, (constant \, a > 0)\) ;\(S\) est la surface délimitée par un cylindre\(x^2 + y^2 = a^2\) et des plans\(z = 0\) et\(z = 1\).

    Réponse
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = \dfrac{9\pi a^4}{2}\)

    9. [T] Intégrale de surface\(\displaystyle \iint_S \vecs F \cdot dS\), où\(S\) est le solide délimité par un paraboloïde\(z = x^2 + y^2\) et un plan\(z = 4\), et\(\vecs F(x,y,z) = (x + y^2z^2)\,\mathbf{\hat i} + (y + z^2x^2)\,\mathbf{\hat j} + (z + x^2y^2) \,\mathbf{\hat k}\)

    10. Utilisez le théorème de divergence pour calculer l'intégrale de surface\(\displaystyle \iint_S \vecs F \cdot dS\), où\(\vecs F(x,y,z) = (e^{y^2} \,\mathbf{\hat i} + (y + \sin (z^2))\,\mathbf{\hat j} + (z - 1)\,\mathbf{\hat k}\) et\(S\) est l'hémisphère supérieur\(x^2 + y^2 + z^2 = 1, \, z \geq 0\), orienté vers le haut.

    Réponse
    \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{\pi}{3}\)

    11. Utilisez le théorème de divergence pour calculer l'intégrale de surface\(\displaystyle \iint_S \vecs F \cdot dS\), où\(\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2z\,\mathbf{\hat k}\) et\(S\) est la surface délimitée par un cylindre\(x^2 + y^2 = 1\) et des plans\(z = x + 2\) et\(z = 0\).

    12. Utilisez le théorème de divergence pour calculer l'intégrale de surface\(\displaystyle \iint_S \vecs F \cdot dS\), quand\(\vecs F(x,y,z) = x^2z^3 \,\mathbf{\hat i} + 2xyz^3\,\mathbf{\hat j} + xz^4 \,\mathbf{\hat k}\) et\(S\) est la surface de la boîte avec des sommets\((\pm 1, \, \pm 2, \, \pm 3)\).

    Réponse
    \(\displaystyle \iint_S \vecs F \cdot dS = 0\)

    13. Utilisez le théorème de divergence pour calculer l'intégrale de surface\(\displaystyle \iint_S \vecs F \cdot dS\), quand\(\vecs F(x,y,z) = z \, \tan^{-1} (y^2)\,\mathbf{\hat i} + z^3 \ln(x^2 + 1) \,\mathbf{\hat j} + z\,\mathbf{\hat k}\) et\(S\) fait partie d'un paraboloïde\(x^2 + y^2 + z = 2\) situé au-dessus du plan\(z = 1\) et orienté vers le haut.

    14. [T] Utilisez un CAS et le théorème de divergence pour calculer le flux\(\displaystyle \iint_S \vecs F \cdot dS\), où\(\vecs F(x,y,z) = (x^3 + y^3)\,\mathbf{\hat i} + (y^3 + z^3)\,\mathbf{\hat j} + (z^3 + x^3)\,\mathbf{\hat k} \) et\(S\) est une sphère avec un centre\((0, 0)\) et un rayon\(2.\)

    Réponse
    \(\displaystyle \iint_S \vecs F \cdot dS = 241.2743\)

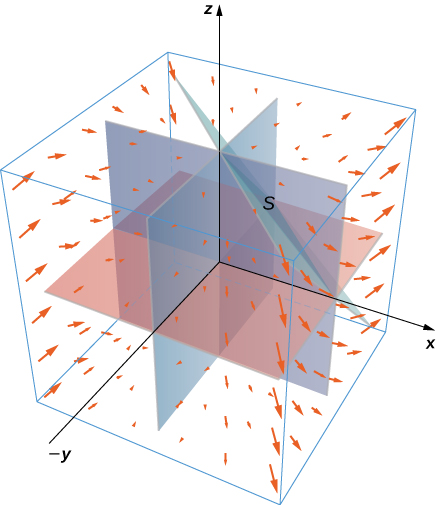
    15. Utilisez le théorème de divergence pour calculer la valeur de l'intégrale du flux\(\displaystyle \iint_S \vecs F \cdot dS\), où\(\vecs F(x,y,z) = (y^3 + 3x)\,\mathbf{\hat i} + (xz + y)\,\mathbf{\hat j} + \left(z + x^4 \cos (x^2y)\right)\,\mathbf{\hat k}\) et\(S\) est l'aire de la région délimitée par\(x^2 + y^2 = 1, \, x \geq 0, \, y \geq 0\), et\(0 \leq z \leq 1\).

    0, y>0, and z>0. A quarter of a cylinder is drawn with center on the z axis. The arrows have positive x, y, and z components; they point away from the origin." data-type="media">Champ vectoriel en trois dimensions, centré sur la zone avec x 0, y>0 et z>0. Un quart de cylindre est dessiné avec son centre sur l'axe Z. Les flèches ont des composantes x, y et z positives ; elles pointent loin de l'origine." src="https://math.libretexts.org/@api/dek...16_08_202.jpeg">

    16. Utiliser le théorème de divergence pour calculer l'intégrale du flux\(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = y\,\mathbf{\hat j} - z\,\mathbf{\hat k}\) and \(S\) consists of the union of paraboloid \(y = x^2 + z^2, \, 0 \leq y \leq 1\), and disk \(x^2 + z^2 \leq 1, \, y = 1\), oriented outward. What is the flux through just the paraboloid?

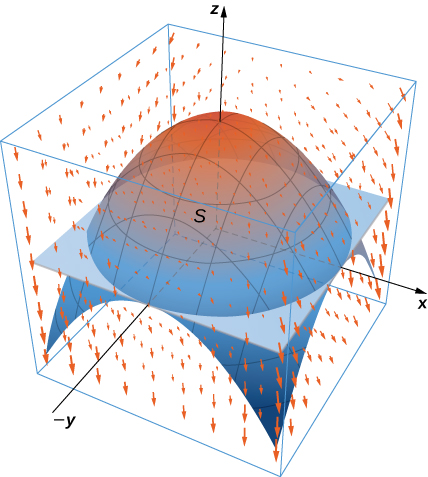
    Answer
    \(\displaystyle \iint_S \vecs F \cdot dS = -\pi\)

    17. Use the divergence theorem to compute flux integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z^4 \,\mathbf{\hat k}\) and \(S\) is a part of cone \(z = \sqrt{x^2 + y^2}\) beneath top plane \(z = 1\) oriented downward.

    18. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\) for \(\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2 z\,\mathbf{\hat k}\), where \(S\) is the surface bounded by cylinder \(x^2 + y^2 = 1\) and planes \(z = x + 2\) and \(z = 0\).

    Answer
    \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{2\pi}{3}\)

    19. Consider \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + xy\,\mathbf{\hat j} + (z + 1)\,\mathbf{\hat k}\). Let \(E\) be the solid enclosed by paraboloid \(z = 4 - x^2 - y^2\) and plane \(z = 0\) with normal vectors pointing outside \(E.\) Compute flux \(\vecs F\) across the boundary of \(E\) using the divergence theorem.

    In exercises 20 - 23, use a CAS along with the divergence theorem to compute the net outward flux for the fields across the given surfaces \(S.\)

    20. [T] \(\vecs F = \langle x,\, -2y, \, 3z \rangle; \) \(S\) is sphere \(\{(x,y,z) : x^2 + y^2 + z^2 = 6 \}\).

    Answer
    \(15\sqrt{6}\pi\)

    21. [T] \(\vecs F = \langle x, \, 2y, \, z \rangle\); \(S\) is the boundary of the tetrahedron in the first octant formed by plane \(x + y + z = 1\).

    22. [T] \(\vecs F = \langle y - 2x, \, x^3 - y, \, y^2 - z \rangle\); \(S\) is sphere \(\{(x,y,z) \,:\, x^2 + y^2 + z^2 = 4\}.\)

    Answer
    \(-\dfrac{128}{3} \pi\)

    23. [T] \(\vecs F = \langle x,y,z \rangle\); \(S\) is the surface of paraboloid \(z = 4 - x^2 - y^2\), for \(z \geq 0\), plus its base in the \(xy\)-plane.

    For exercises 24 - 26, use a CAS and the divergence theorem to compute the net outward flux for the vector fields across the boundary of the given regions \(D.\)

    24. [T] \(\vecs F = \langle z - x, \, x - y, \, 2y - z \rangle\); \(D\) is the region between spheres of radius 2 and 4 centered at the origin.

    Answer
    \(-703.7168\)

    25. [T] \(\vecs F = \dfrac{\vecs r}{\|\vecs r\|} = \dfrac{\langle x,y,z\rangle}{\sqrt{x^2+y^2+z^2}}\); \(D\) is the region between spheres of radius 1 and 2 centered at the origin.

    26. [T] \(\vecs F = \langle x^2, \, -y^2, \, z^2 \rangle\); \(D\) is the region in the first octant between planes \(z = 4 - x - y\) and \(z = 2 - x - y\).

    Answer
    \(20\)

    27. Let \(\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3xy\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\). Use the divergence theorem to calculate \(\displaystyle \iint_S \vecs F \cdot dS\), where \(S\) is the surface of the cube with corners at \((0,0,0), \, (1,0,0), \, (0,1,0), \, (1,1,0), \, (0,0,1), \, (1,0,1), \, (0,1,1)\), and \((1,1,1)\), oriented outward.

    28. Use the divergence theorem to find the outward flux of field \(\vecs F(x,y,z) = (x^3 - 3y)\,\mathbf{\hat i} + (2yz + 1)\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}\) through the cube bounded by planes \(x = \pm 1, \, y = \pm 1, \) and \(z = \pm 1\).

    Answer
    \(\displaystyle \iint_S \vecs F \cdot dS = 8\)

    29. Let \(\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3y\,\mathbf{\hat j} + 5z\,\mathbf{\hat k}\) and let \(S\) be hemisphere \(z = \sqrt{9 - x^2 - y^2}\) together with disk \(x^2 + y^2 \leq 9\) in the \(xy\)-plane. Use the divergence theorem.

    30. Evaluate \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS\), where \(\vecs F(x,y,z) = x^2 \,\mathbf{\hat i} + xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}\) and \(S\) is the surface consisting of all faces except the tetrahedron bounded by plane \(x + y + z = 1\) and the coordinate planes, with outward unit normal vector \(\vecs N.\)

    A vector field in three dimensions, with arrows becoming larger the further away from the origin they are, especially in their x components. S is the surface consisting of all faces except the tetrahedron bounded by the plane x + y + z = 1. As such, a portion of the given plane, the (x, y) plane, the (x, z) plane, and the (y, z) plane are shown. The arrows point towards the origin for negative x components, away from the origin for positive x components, down for positive x and negative y components, as well as positive y and negative x components, and for positive x and y components, as well as negative x and negative y components.

    Réponse
    \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS = \dfrac{1}{8}\)

    31. Déterminez le flux net de champ sortant\(\vecs F = \langle bz - cy, \, cx - az, \, ay - bx \rangle\) sur toute surface lisse fermée à l'\(R^3\)endroit où\(a, \, b,\) et\(c\) sont des constantes.

    32. Utilisez le théorème de divergence pour évaluer\(\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds,\) où\(\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) et\(S\) est la sphère\(x^2 + y^2 + z^2 = a^2\), avec une constante\(a > 0\).

    Réponse
    \(\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds = 4\pi a^4\)

    33. Utilisez le théorème de divergence pour évaluer\(\displaystyle \iint_S \vecs F \cdot dS,\) où\(\vecs F(x,y,z) = y^2 z\,\mathbf{\hat i} + y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}\) et\(S\) se trouve la limite du cube définie par\(-1 \leq x \leq 1, \, -1 \leq y \leq 1\), et\(0 \leq z \leq 2\).

    34. \(R\)Soyons la région définie par\(x^2 + y^2 + z^2 \leq 1\). Utilisez le théorème de divergence pour trouver\(\displaystyle \iiint_R z^2 \, dV.\)

    Réponse
    \(\displaystyle \iiint_R z^2 dV = \dfrac{4\pi}{15}\)

    35. \(E\)Soit le solide délimité par le\(xy\) plan -et le paraboloïde,\(z = 4 - x^2 - y^2\) c'\(S\)est-à-dire la surface de la pièce paraboloïde avec le disque dans le\(xy\) plan -qui forme son fond. Si\(\vecs F(x,y,z) = (xz \, \sin(yz) + x^3) \,\mathbf{\hat i} + \cos (yz) \,\mathbf{\hat j} + (3zy^2 - e^{x^2+y^2})\,\mathbf{\hat k}\), trouvez\(\displaystyle \iint_S \vecs F \cdot dS\) en utilisant le théorème de divergence.

    Un champ vectoriel en trois dimensions avec toutes les flèches pointant vers le bas. Ils semblent suivre la trajectoire du paraboloïde dessiné s'ouvrant vers le bas avec un sommet à l'origine. S est la surface de ce paraboloïde et le disque dans le plan (x, y) qui forme son fond.

    36. Laissez

    Template:ContribOpenStaxCalc