Skip to main content
Global

15.7E : Exercices pour la section 15.7

  1. Last updated
  2. Save as PDF
  • Page ID
    197482

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 6, la fonction\(T : S \rightarrow R, \space T (u,v) = (x,y)\) sur la région\(S = \big\{(u,v) \,|\, 0 \leq u \leq 1, \space 0 \leq v \leq 1\big\}\) délimitée par l'unité carrée est donnée, où se\(R \in R^2\) trouve l'image du\(S\) dessous\(T\).

    a. Justifiez que la fonction\(T\) est une\(C^1\) transformation.

    b. Trouvez les images des sommets de l'unité de carré\(S\) à l'aide de la fonction\(T\).

    c. Déterminez l'image\(R\) du carré de l'unité\(S\) et représentez-la graphiquement.

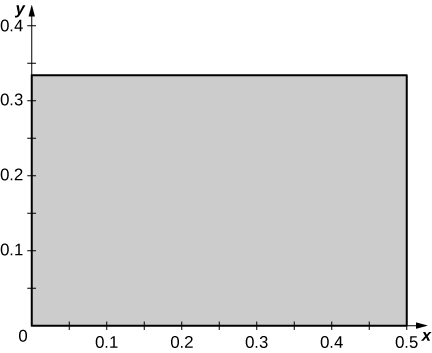
    1. \(x = 2u, \space y = 3v\)

    2. \(x = \frac{u}{2}, \space y = \frac{v}{3}\)

    Réponse

    a.\(T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = \frac{u}{2}\) et\(y = h(u,v) = \frac{v}{3}\). Les fonctions\(g\) et\(h\) sont continues et dérivables, et les dérivées\(g_u (u,v) = \frac{1}{2}, \space g_v (u,v) = 0, \space h_u (u,v) = 0\) partielles\(h_v (u,v) = \frac{1}{3}\) sont continues\(S\) ;

    b.\(T(0,0) = (0,0), \space T(1,0) = \left(\frac{1}{2},0\right), \space T(0,1) = \left(0,\frac{1}{3}\right)\), et\(T(1,1) = \left(\frac{1}{2}, \frac{1}{3} \right)\) ;

    c.\(R\) est le rectangle de sommets\((0,0), \space \left(0,\frac{1}{3}\right), \space \left(\frac{1}{2}, \frac{1}{3} \right)\), et\(\left(0,\frac{1}{3}\right)\) dans le\(xy\) plan -; la figure suivante.

    Un rectangle avec un coin à l'origine, une longueur horizontale de 0,5 et une hauteur verticale de 0,34.

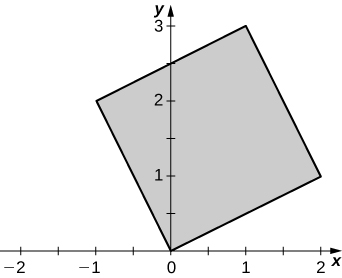
    3. \(x = u - v, \space y = u + v\)

    4. \(x = 2u - v, \space y = u + 2v\)

    Answer

    a. \(T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = 2u - v\) and \(y = h(u,v) = u + 2v\). The functions \(g\) and \(h\) are continuous and differentiable, and the partial derivatives \(g_u (u,v) = 2, \space g_v (u,v) = -1, \space h_u (u,v) = 1\) and \(h_v (u,v) = 2\) are continuous on \(S\);

    b. \(T(0,0) = (0,0), \space T(1,0) = (2,1), \space T(0,1) = (-1,2)\), and \(T(1,1) = (1,3)\);

    c. \(R\) is the parallelogram of vertices \((0,0), \space (2,1) \space (1,3)\), and \((-1,2)\) in the \(xy\)-plane; the following figure.

    A square of side length square root of 5 with one corner at the origin and another at (2, 1).

    5. \(x = u^2, \space y = v^2\)

    6. \(x = u^3, \space y = v^3\)

    Réponse

    a.\(T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = u^3\) et\(y = h(u,v) = v^3\). Les fonctions\(g\) et\(h\) sont continues et dérivables, et les dérivées\(g_u (u,v) = 3u^2, \space g_v (u,v) = 0, \space h_u (u,v) = 0\) partielles\(h_v (u,v) = 3v^2\) sont continues\(S\) ;

    b.\(T(0,0) = (0,0), \space T(1,0) = (1,0), \space T(0,1) = (0,1)\), et\(T(1,1) = (1,1)\) ;

    c.\(R\) est l'unité carrée dans le\(xy\) plan (voir la figure dans la réponse à l'exercice précédent).

    Dans les exercices 7 à 12, déterminez si les transformations\(T : S \rightarrow R\) sont biunivoques ou non.

    7. \(x = u^2, \space y = v^2\), où\(S\) est le rectangle de sommets\((-1,0), \space (1,0), \space (1,1)\), et\((-1,1)\).

    8. \(x = u^4, \space y = u^2 + v\), où\(S\) se trouve le triangle des sommets\((-2,0), \space (2,0)\), et\((0,2)\).

    Réponse
    \(T\)n'est pas un à un : deux points\(S\) ont la même image. En effet,\(T(-2,0) = T(2,0) = (16,4)\).

    9. \(x = 2u, \space y = 3v\), où\(S\) est le carré des sommets\((-1,1), \space (-1,-1), \space (1,-1)\), et\((1,1)\).

    10. \(T(u, v) = (2u - v, u),\)où\(S\) est le triangle avec des sommets\((-1,1), \, (-1,-1)\), et\((1,-1)\).

    Réponse
    \(T\)est un à un : nous argumentons par contradiction. \(T(u_1,v_1) = T(u_2,v_2)\)implique\(2u_1 - v_1 = 2u_2 - v_2\) et\(u_1 = u_2\). Ainsi,\(u_1 = u+2\) et\(v_1 = v_2\).

    11. \(x = u + v + w, \space y = u + v, \space z = w\), où\(S = R = R^3\).

    12. \(x = u^2 + v + w, \space y = u^2 + v, \space z = w\), où\(S = R = R^3\).

    Réponse
    \(T\)n'est pas un à un :\(T(1,v,w) = (-1,v,w)\)

    Dans les exercices 13 à 18, les transformations\(T : R \rightarrow S\) se font une à une. Trouvez leurs transformations inverses associées\(T^{-1} : R \rightarrow S\).

    13. \(x = 4u, \space y = 5v\), où\(S = R = R^2\).

    14. \(x = u + 2v, \space y = -u + v\), où\(S = R = R^2\).

    Réponse
    \(u = \frac{x-2y}{3}, \space v= \frac{x+y}{3}\)

    15. \(x = e^{2u+v}, \space y = e^{u-v}\), où\(S = R^2\) et\(R = \big\{(x,y) \,|\, x > 0, \space y > 0\big\}\)

    16. \(x = \ln u, \space y = \ln(uv)\), où\(S = \big\{(u,v) \,|\, u > 0, \space v > 0\big\}\) et\(R = R^2\).

    Réponse
    \(u = e^x, \space v = e^{-x+y}\)

    17. \(x = u + v + w, \space y = 3v, \space z = 2w\), où\(S = R = R^3\).

    18. \(x = u + v, \space y = v + w, \space z = u + w\), où\(S = R = R^3\).

    Réponse
    \(u = \frac{x-y+z}{2}, \space v = \frac{x+y-z}{2}, \space w = \frac{-x+y+z}{2}\)

    Dans les exercices 19 à 22, la transformation\(T : S \rightarrow R, \space T (u,v) = (x,y)\) et la région\(R \subset R^2\) sont données. Trouvez la région\(S \subset R^2\).

    19. \(x = au, \space y = bv, \space R = \big\{(x,y) \,|\, x^2 + y^2 \leq a^2 b^2\big\}\)où\(a,b > 0\)

    20. \(x = au, \space y = bc, \space R = \big\{(x,y) \,|\, \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1\big\}\), où\(a,b > 0\)

    Réponse
    \(S = \big\{(u,v) \,|\, u^2 + v^2 \leq 1\big\}\)

    21. \(x = \frac{u}{a}, \space y = \frac{v}{b}, \space z = \frac{w}{c}, \space R = \big\{(x,y)\,|\,x^2 + y^2 + z^2 \leq 1\big\}\), où\(a,b,c > 0\)

    22. \(x = au, \space y = bv, \space z = cw, \space R = \big\{(x,y)\,|\,\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} \leq 1, \space z > 0\big\}\), où\(a,b,c > 0\)

    Réponse
    \(R = \big\{(u,v,w)\,|\,u^2 - v^2 - w^2 \leq 1, \space w > 0\big\}\)

    Dans les exercices 23 à 32, trouvez le jacobien\(J\) de la transformation.

    23. \(x = u + 2v, \space y = -u + v\)

    24. \(x = \frac{u^3}{2}, \space y = \frac{v}{u^2}\)

    Réponse
    \(\frac{3}{2}\)

    25. \(x = e^{2u-v}, \space y = e^{u+v}\)

    26. \(x = ue^v, \space y = e^{-v}\)

    Réponse
    \(-1\)

    27. \(x = u \space \cos (e^v), \space y = u \space \sin(e^v)\)

    28. \(x = v \space \sin (u^2), \space y = v \space \cos(u^2)\)

    Réponse
    \(2uv\)

    29. \(x = u \space \cosh v, \space y = u \space \sinh v, \space z = w\)

    30. \(x = v \space \cosh \left(\frac{1}{u}\right), \space y = v \space \sinh \left(\frac{1}{u}\right), \space z = u + w^2\)

    Réponse
    \(\frac{v}{u^2}\)

    31. \(x = u + v, \space y = v + w, \space z = u\)

    32. \(x = u - v, \space y = u + v, \space z = u + v + w\)

    Réponse
    \(2\)

    33. La région triangulaire\(R\) avec les sommets\((0,0), \space (1,1)\), et\((1,2)\) est illustrée dans la figure suivante.

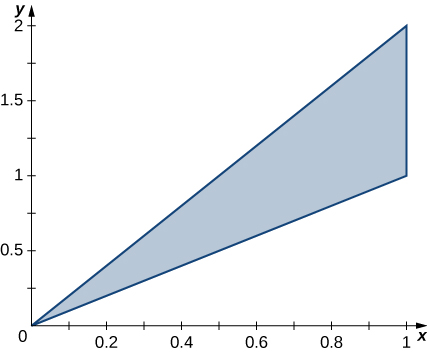
    Un triangle avec des coins à l'origine, (1, 1) et (1, 2).

    a. Trouvez une transformation\(T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)\), where \(a,b,c\), and \(d\) are real numbers with \(ad - bc \neq 0\) such that \(T^{-1} (0,0) = (0,0), \space T^{-1} (1,1) = (1,0)\), and \(T^{-1}(1,2) = (0,1)\).

    b. Use the transformation \(T\) to find the area \(A(R)\) of the region \(R\).

    34. The triangular region \(R\) with the vertices \((0,0), \space (2,0)\), and \((1,3)\) is shown in the following figure.

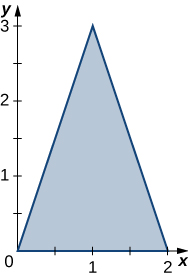
    A triangle with corners at the origin, (2, 0), and (1, 3).

    a. Trouvez une transformation\(T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)\)\(a,b,c\), où et\(d\) sont des nombres réels avec des valeurs\(ad - bc \neq 0\) telles que\(T^{-1} (0,0) = (0,0), \space T^{-1} (2,0) = (1,0)\), et\(T^{-1}(1,3) = (0,1)\).

    b. Utilisez la transformation\(T\) pour trouver la superficie\(A(R)\) de la région\(R\).

    Réponse

    a.\(T (u,v) = (2u + v, \space 3v)\)
    b. La superficie\(R\) de\(\displaystyle A(R) = \int_0^3 \int_{y/3}^{(6-y)/3} \, dx \, dy = \int_0^1 \int_0^{1-u} \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \, dv \space du = \int_0^1 \int_0^{1-u} 6 \, dv \, du = 3.\)

    Dans les exercices 35 à 36, utilisez la transformation\(u = y - x, \space v = y\) pour évaluer les intégrales sur le parallélogramme\(R\) des sommets\((0,0), \space (1,0), \space (2,1)\),\((1,1)\) comme illustré dans la figure suivante.

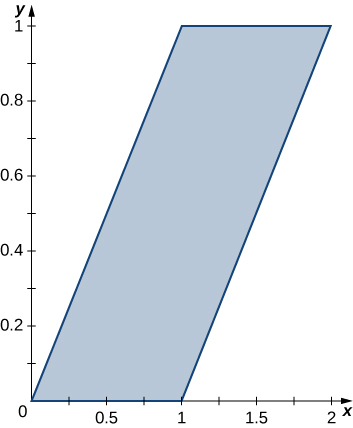
    Un losange avec des coins à l'origine, (1, 0), (1, 1) et (2, 1).

    35. \(\displaystyle \iint_R (y - x) \, dA\)

    36. \(\displaystyle \iint_R (y^2 - xy) \, dA\)

    Answer
    \(-\frac{1}{4}\)

    In exercises 37 - 38, use the transformation \(y = x = u, \space x + y = v\) to evaluate the integrals on the square \(R\) determined by the lines \(y = x, \space y = -x + 2, \space y = x + 2\), and \(y = -x\) shown in the following figure.

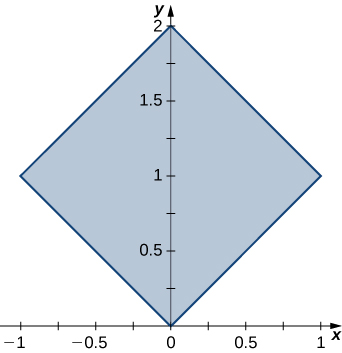
    A square with side lengths square root of 2 rotated 45 degrees with one corner at the origin and another at (1, 1).

    37. \(\displaystyle \iint_R e^{x+y} \, dA\)

    38. \(\displaystyle \iint_R \sin (x - y) \, dA\)

    Réponse
    \(-1 + \cos 2\)

    Dans les exercices 39 à 40, utilisez la transformation\(x = u, \space 5y = v\) pour évaluer les intégrales de la région\(R\) délimitée par l'ellipse\(x^2 + 25y^2 = 1\) illustrée dans la figure suivante.

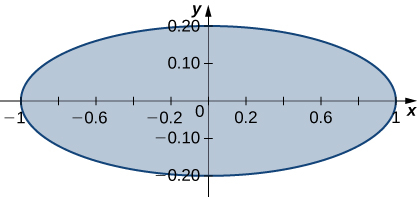
    Ellipse dont le centre est à l'origine, le grand axe 2 et le petit 0,4.

    39. \(\displaystyle \iint_R \sqrt{x^2 + 25y^2} \, dA\)

    40. \(\displaystyle \iint_R (x^2 + 25y^2)^2 \, dA\)

    Answer
    \(\frac{\pi}{15}\)

    In exercises 41 - 42, use the transformation \(u = x + y, \space v = x - y\) to evaluate the integrals on the trapezoidal region \(R\) determined by the points \((1,0), \space (2,0), \space (0,2)\), and \((0,1)\) shown in the following figure.

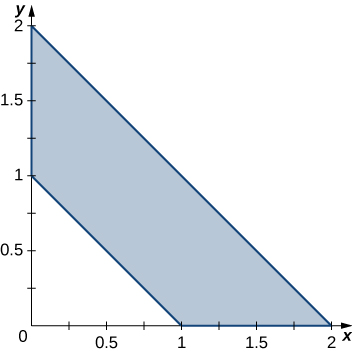
    A trapezoid with corners at (1, 0), (0, 1), (0, 2), and (2, 0).

    41. \(\displaystyle \iint_R (x^2 - 2xy + y^2) \space e^{x+y} \, dA\)

    42. \(\displaystyle \iint_R (x^3 + 3x^2y + 3xy^2 + y^3) \, dA\)

    Réponse
    \(\frac{31}{5}\)

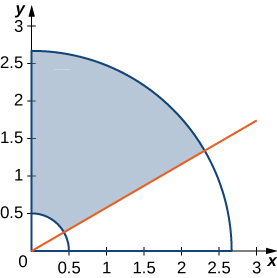
    43. Le secteur annulaire circulaire\(R\) délimité par les cercles\(4x^2 + 4y^2 = 1\) et\(9x^2 + 9y^2 = 64\), la ligne\(x = y \sqrt{3}\) et l'\(y\)axe y est illustré dans la figure suivante. Trouvez une transformation\(T\) d'une région rectangulaire\(S\) dans le\(r\theta\) plan -vers la\(R\) région du\(xy\) plan. Graphe\(S\).

    Dans le premier quadrant, une section d'un anneau décrite par un rayon intérieur de 0,5, un rayon extérieur légèrement supérieur à 2,5 et un centre de l'origine. Il y a une ligne qui divise cet anneau et qui part d'un angle d'environ 30 degrés. La partie correspondant à 60 degrés est ombrée.

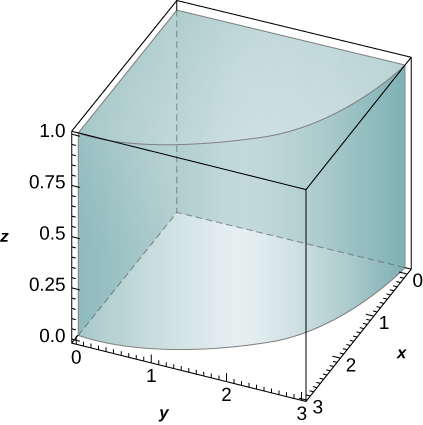
    44. Le solide\(R\) bounded by the circular cylinder \(x^2 + y^2 = 9\) and the planes \(z = 0, \space z = 1, \space x = 0\), and \(y = 0\) is shown in the following figure. Find a transformation \(T\) from a cylindrical box \(S\) in \(r\theta z\)-space to the solid \(R\) in \(xyz\)-space.

    A quarter of a cylinder with height 1 and radius 3. The center axis is the z axis.

    Réponse
    \(T (r,\theta,z) = (r \space \cos \theta, \space r \space \sin \theta, \space z); \space S = [0,3] \times [0,\frac{\pi}{2}] \times [0,1]\)dans l'\(r\theta z\)espace

    45. Montrez que l'\[\iint_R f \left(\sqrt{\frac{x^2}{3} + \frac{y^2}{3}}\right) dA = 2 \pi \sqrt{15} \int_0^1 f (\rho) \rho \space d\rho, \nonumber \]endroit où\(f\) se\(R\) trouve une fonction continue\([0,1]\) et la région délimitée par l'ellipse\(5x^2 + 3y^2 = 15\).

    46. Montrez que l'\[\iiint_R f \left(\sqrt{16x^2 + 4y^2 + z^2}\right) dV = \frac{\pi}{2} \int_0^1 f (\rho) \rho^2 d\rho, \nonumber \]endroit où\(f\) se\(R\) trouve une fonction continue\([0,1]\) et la région délimitée par l'ellipsoïde\(16x^2 + 4y^2 + z^2 = 1\).

    47. [T] Trouvez l'aire de la région délimitée par les courbes\(xy = 1, \space xy = 3, \space y = 2x\), et\(y = 3x\) en utilisant la transformation\(u = xy\) et\(v = \frac{y}{x}\). Utilisez un système d'algèbre informatique (CAS) pour représenter graphiquement les courbes limites de la région\(R\).

    48. [T] Trouvez l'aire de la région délimitée par les courbes\(x^2y = 2, \space x^2y = 3, \space y = x\), et\(y = 2x\) en utilisant la transformation\(u = x^2y\) et\(v = \frac{y}{x}\). Utilisez un CAS pour représenter graphiquement les courbes limites de la région\(R\).

    Réponse

    L'aire de\(R\) est\(10 - 4\sqrt{6}\) ; les courbes limites de\(R\) sont représentées graphiquement dans la figure suivante.

    Quatre lignes sont tracées, à savoir y = 3, y = 2, y = 3/ (x carré) et y = 2/ (x carré). Les lignes y = 3 et y = 2 sont parallèles entre elles. Les lignes y = 3/ (x carré) et y = 2/ (x carré) sont des courbes légèrement parallèles entre elles.

    49. Evaluer la triple intégrale\[\int_0^1 \int_1^2 \int_z^{z+1} (y + 1) \space dx \space dy \space dz \nonumber \] by using the transformation \(u = x - z, \space v = 3y\), and \(w = \frac{z}{2}\).

    50. Evaluate the triple integral \[\int_0^2 \int_4^6 \int_{3z}^{3z+2} (5 - 4y) \space dx \space dy \space dz \nonumber \] by using the transformation \(u = x - 3z, \space v = 4y\), and \(w = z\).

    Answer
    \(8\)

    51. A transformation \(T : R^2 \rightarrow R^2, \space T (u,v) = (x,y)\) of the form \(x = au + bv, \space y = cu + dv\), where \(a,b,c\), and \(d\) are real numbers, is called linear. Show that a linear transformation for which \(ad - bc \neq 0\) maps parallelograms to parallelograms.

    52. A transformation \(T_{\theta} : R^2 \rightarrow R^2, \space T_{\theta} (u,v) = (x,y)\) of the form \(x = u \space \cos \theta - v \space \sin \theta, \space y = u \space \sin \theta + v \space \cos \theta\), is called a rotation angle \(\theta\). Show that the inverse transformation of \(T_{\theta}\) satisfies \(T_{\theta}^{-1} = T_{-\theta}\) where \(T_{-\theta}\) is the rotation of angle \(-\theta\).

    53. [T] Find the region \(S\) in the \(uv\)-plane whose image through a rotation of angle \(\frac{\pi}{4}\) is the region \(R\) enclosed by the ellipse \(x^2 + 4y^2 = 1\). Use a CAS to answer the following questions.

    a. Graph the region \(S\).

    b. Evaluate the integral \(\displaystyle \iint_S e^{-2uv} \, du \, dv.\) Round your answer to two decimal places.

    54. [T] The transformations \(T_i : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space i = 1, . . . , 4,\) defined by \(T_1(u,v) = (u,-v), \space T_2 (u,v) = (-u,v), \space T_3 (u,v) = (-u, -v)\), and \(T_4 (u,v) = (v,u)\) are called reflections about the \(x\)-axis, \(y\)-axis origin, and the line \(y = x\), respectively.

    a. Find the image of the region \(S = \big\{(u,v)\,|\,u^2 + v^2 - 2u - 4v + 1 \leq 0\big\}\) in the \(xy\)-plane through the transformation \(T_1 \circ T_2 \circ T_3 \circ T_4\).

    b. Use a CAS to graph \(R\).

    c. Evaluate the integral \(\displaystyle \iint_S \sin (u^2) \, du \, dv\) by using a CAS. Round your answer to two decimal places.

    Answer

    a. \(R = \big\{(x,y)\,|\,y^2 + x^2 - 2y - 4x + 1 \leq 0\big\}\);
    b. \(R\) is graphed in the following figure;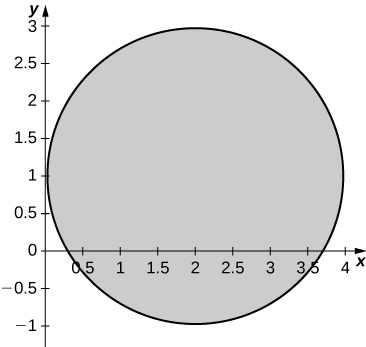

    A circle with radius 2 and center (2, 1).

    c.\(3.16\)

    55. [T] Les transformations\(T_{k,1,1} : \mathbb{R}^3 \rightarrow \mathbb{R}^3, \space T_{k,1,1}(u,v,w) = (x,y,z)\) de la forme\(x = ku, \space y = v, \space z = w\), où\(k \neq 1\) est un nombre réel positif, sont appelées étirement\(k > 1\) et compression si elles se\(0 < k < 1\) situent dans la\(x\) direction. Utilisez un CAS pour évaluer l'intégrale\(\displaystyle \iiint_S e^{-(4x^2+9y^2+25z^2)} \, dx \, dy \, dz\) du solide\(S = \big\{(x,y,z) \,|\, 4x^2 + 9y^2 + 25z^2 \leq 1\big\}\) en tenant compte de la compression\(T_{2,3,5}(u,v,w) = (x,y,z)\) définie par\(x = \frac{u}{2}, \space y = \frac{v}{3}\), et\(z = \frac{w}{5}\). Arrondissez votre réponse à quatre décimales.

    56. [T] La transformation\(T_{a,0} : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space T_{a,0} (u,v) = (u + av, v)\), où\(a \neq 0\) est un nombre réel, est appelée cisaillement dans la\(x\) direction. La transformation\(T_{b,0} : R^2 \rightarrow R^2, \space T_{o,b}(u,v) = (u,bu + v)\), où\(b \neq 0\) est un nombre réel, est appelée cisaillement dans la\(y\) direction.

    a. Trouvez des transformations\(T_{0,2} \circ T_{3,0}\).

    b. Trouvez l'image\(R\) de la région trapézoïdale\(S\) délimitée par\(u = 0, \space v = 0, \space v = 1\) et\(v = 2 - u\) à travers la transformation\(T_{0,2} \circ T_{3,0}\).

    c. Utilisez un CAS pour représenter graphiquement l'image\(R\) dans le\(xy\) plan.

    d. Trouvez la superficie de la région\(R\) en utilisant la superficie de la région\(S\).

    Réponse

    un\(T_{0,2} \circ T_{3,0}(u,v) = (u + 3v, 2u + 7v)\) ;.

    b. L'image\(S\) est le quadrilatère de sommets\((0,0), \space (3,7), \space (2,4)\), et\((4,9)\) ;

    c.\(S\) est représenté graphiquement dans la figure suivante ;

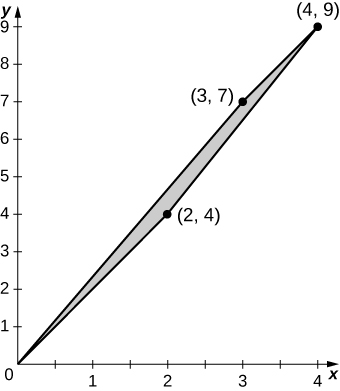
    Figure à quatre faces avec des points sur l'origine, (2, 4), (4, 9) et (3, 7).

    d.

    Template:ContribOpenStaxCalc