15.5 : Intégrales triples en coordonnées cylindriques et sphériques
- Page ID
- 197491
- Évaluez une intégrale triple en utilisant des coordonnées cylindriques.
- Evaluez une triple intégrale en la remplaçant par des coordonnées sphériques.
Plus tôt dans ce chapitre, nous avons montré comment convertir une intégrale double en coordonnées rectangulaires en une intégrale double en coordonnées polaires afin de traiter plus facilement les problèmes liés à la symétrie circulaire. Une situation similaire se produit avec les intégrales triples, mais nous devons ici faire la distinction entre la symétrie cylindrique et la symétrie sphérique. Dans cette section, nous convertissons des intégrales triples en coordonnées rectangulaires en une intégrale triple en coordonnées cylindriques ou sphériques.
Rappelez-vous également le prélude du chapitre, qui présentait l'opéra L'Hemisphèric à Valence, en Espagne. Il comprend quatre sections, l'une des sections étant un théâtre dans une sphère de cinq étages (balle) sous un toit ovale aussi long qu'un terrain de football. À l'intérieur se trouve un écran IMAX qui transforme la sphère en planétarium avec un ciel plein d'étoiles\(9000\) scintillantes. En utilisant des intégrales triples en coordonnées sphériques, nous pouvons trouver les volumes de différentes formes géométriques comme celles-ci.
Révision des coordonnées cylindriques
Comme nous l'avons vu précédemment, dans\(\mathbb{R}^2\) un espace bidimensionnel, un point avec des coordonnées rectangulaires\((x,y)\) peut être identifié\((r,\theta)\) en coordonnées polaires et vice versa\(x = r \, \cos \theta\), où\(y = r \, \sin \, \theta, \, r^2 = x^2 + y^2\) et\(\tan \, \theta = \left(\frac{y}{x}\right)\) sont les relations entre les variables.
Dans l'espace tridimensionnel,\(\mathbb{R}^3\) un point avec des coordonnées rectangulaires\((x,y,z)\) peut être identifié par des coordonnées cylindriques\((r, \theta, z)\) et vice versa. Nous pouvons utiliser ces mêmes relations de conversion, en ajoutant\(z\) comme distance verticale entre le point et le\((xy\) plan, comme indiqué à la\(\PageIndex{1}\).
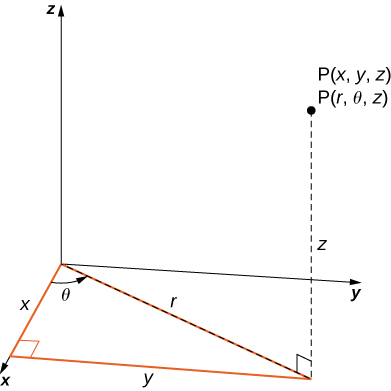
Pour convertir des coordonnées rectangulaires en coordonnées cylindriques, nous utilisons la conversion
- \(x = r \, \cos \theta\)
- \(y = r \, \sin \, \theta\)
- \(z=z\)
Pour convertir des coordonnées cylindriques en coordonnées rectangulaires, nous utilisons
- \(r^2 = x^2 + y^2\)et
- \(\theta = \tan^{-1} \left(\frac{y}{x}\right)\)
- \(z=z\)
Notez que cette\(z\) coordonnée reste la même dans les deux cas.
Dans le plan bidimensionnel avec un système de coordonnées rectangulaires, lorsque nous disons\(x = k\) (constante), nous entendons une ligne verticale illimitée parallèle à l'\(y\)axe et lorsque\(y = l\) (constante), nous entendons une ligne horizontale illimitée parallèle à l'\(x\)axe. Avec le système de coordonnées polaires, lorsque nous disons\(r = c\) (constant), nous entendons un cercle d'\(c\)unités de rayon et lorsque\(\theta = \alpha\) (constant) nous entendons un rayon infini faisant un angle\(\alpha\) avec l'\(x\)axe positif.
De même, dans un espace tridimensionnel\((x,y,z)\) aux coordonnées rectangulaires, les équations\(x = k, \, y = l\)\(k, \, l\) et\(z = m\) où et\(m\) sont des constantes représentent des plans illimités parallèles au\(yz\) plan, au\(xz\) plan et au\(xy\) plan, respectivement. Avec des coordonnées cylindriques\((r, \theta, z)\)\(r = c, \, \theta = \alpha\), by\(z = m\), et\(c, \alpha\), où et\(m\) sont des constantes, nous entendons un cylindre vertical illimité dont l'axe radial est l'axe z ; un plan faisant un angle constant\(\alpha\) avec le\(xy\) plan -; et un plan horizontal illimité parallèlement au\(xy\) plan -, respectivement. Cela signifie que le cylindre circulaire\(x^2 + y^2 = c^2\) en coordonnées rectangulaires peut être représenté simplement comme\(r = c\) en coordonnées cylindriques. (Reportez-vous aux coordonnées cylindriques et sphériques pour plus de détails.)
Intégration dans les coordonnées cylindriques
Les intégrales triples peuvent souvent être évaluées plus facilement en utilisant des coordonnées cylindriques plutôt que des coordonnées rectangulaires. Certaines équations courantes de surfaces en coordonnées rectangulaires ainsi que les équations correspondantes en coordonnées cylindriques sont répertoriées dans le tableau\(\PageIndex{1}\). Ces équations seront utiles lorsque nous procéderons à la résolution de problèmes à l'aide d'intégrales triples.
| Cylindre circulaire | Cône circulaire | sphère | Paraboloïde | |
|---|---|---|---|---|
| rectangulaire | \(x^2 + y^2 = c^2\) | \(z^2 = c^2 (x^2 + y^2)\) | \(x^2 + y^2 + z^2 = c^2\) | \(z = c(x^2 + y^2)\) |
| cylindrique | \(r = c\) | \(z = cr\) | \(r^2 + z^2 = c^2\) | \(z = cr^2\) |
Comme précédemment, nous commençons par la région bornée la\(B\) plus simple\(\mathbb{R}^3\) à décrire en coordonnées cylindriques, sous la forme d'une boîte cylindrique\(B = \{(r,\theta,z) | a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}\) (Figure\(\PageIndex{2}\)). Supposons que nous divisions chaque intervalle en\(l, \, m\), et\(n\) subdivisions telles que\(\Delta r = \frac{b \cdot a}{l}, \, \Delta \theta = \frac{\beta \cdot \alpha}{m}\), et\(\Delta z = \frac{d \cdot c}{n}\). Ensuite, nous pouvons énoncer la définition suivante pour une intégrale triple en coordonnées cylindriques.
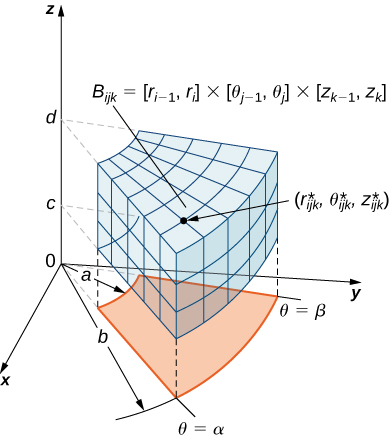
Considérez la boîte cylindrique (exprimée en coordonnées cylindriques)
\[B = \{(r, \theta, z)|a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}. \nonumber \]
Si la fonction\(f(r, \theta, z)\) est continue\(B\) et qu'il s'\((r_{ijk}^*, \theta_{ijk}^*, z_{ijk}^*)\)agit d'un point d'échantillonnage dans la sous-boîte cylindrique\(B_{ijk} = |r_{i-1}, r_i| \times |\theta_{j-1}, \theta_j| \times |z_{k-1}, k_i|\) (Figure\(\PageIndex{2}\)), nous pouvons définir la triple intégrale en coordonnées cylindriques comme la limite d'une triple somme de Riemann, à condition que la limite suivante existe :
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(r_{ijk}^*, \theta_{ijk}^*, z_{ijk}^*) \Delta r \Delta \theta \Delta z. \nonumber \]
Notez que si\(g(x,y,z)\) est la fonction en coordonnées rectangulaires et que la boîte\(B\) est exprimée en coordonnées rectangulaires, alors la triple intégrale
\[\iiint_B g(x,y,z)dV \nonumber \]
est égal à la triple intégrale
\[\iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz \nonumber \]
et nous avons
\[\iiint_B g(x,y,z)dV = \iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz = \iiint_B f(r, \theta \, z) r \, dr \, d\theta \, dz. \nonumber \]
Comme indiqué dans la section précédente, toutes les propriétés d'une intégrale double fonctionnent bien dans les intégrales triples, que ce soit en coordonnées rectangulaires ou en coordonnées cylindriques. Ils s'appliquent également aux intégrales itérées. Pour réitérer, en coordonnées cylindriques, le théorème de Fubini prend la forme suivante :
Supposons que cela\(g(x,y,z)\) soit continu sur une boîte rectangulaire\(B\) qui, lorsqu'elle est décrite en coordonnées cylindriques, ressemble à\(B = \{(r,\theta,z) | a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}\).
Puis\(g(x,y,z) = g(r \, \cos \theta, r \, \sin \, \theta,z) = f(r, \theta,z)\) et
\[\iiint_B g(x,y,z)dV = \int_c^d \int_{\beta}^{\alpha} \int_a^b f(r, \theta, z) r \, dr \, d\theta \, dz. \nonumber \]
L'intégrale itérée peut être remplacée de manière équivalente par n'importe laquelle des cinq autres intégrales itérées obtenues par intégration par rapport aux trois variables dans d'autres ordres.
Les systèmes de coordonnées cylindriques fonctionnent bien pour les solides symétriques autour d'un axe, tels que les cylindres et les cônes. Examinons quelques exemples avant de définir l'intégrale triple en coordonnées cylindriques sur des régions cylindriques générales.
Evaluer la triple intégrale
\[\iiint_B (zr \, \sin \, \theta) r \, dr \, d\theta \, dz \nonumber \]
où se trouve la boîte\(B\) cylindrique\(B = \{(r,\theta,z) |0 \leq r \leq 2, \, 0 \leq \theta \leq \pi/2, \, 0, \leq z \leq 4\}.\)
Solution
Comme indiqué dans le théorème de Fubini, nous pouvons écrire l'intégrale triple comme l'intégrale itérée
\[\iiint_B (zr \, \sin \, \theta) r \, dr \, d\theta \, dz = \int_{\theta=0}^{\theta=\pi/2} \int_{r=0}^{r=2} \int_{z=0}^{z=4} (zr \, \sin \, \theta) r \, dz \, dr \, d\theta. \nonumber \]
L'évaluation de l'intégrale itérée est simple. Chaque variable de l'intégrale est indépendante des autres, de sorte que nous pouvons intégrer chaque variable séparément et multiplier les résultats ensemble. Cela facilite grandement le calcul :
\[\int_{\theta=0}^{\theta=\pi/2} \int_{r=0}^{r=2} \int_{z=0}^{z=4} (zr \, \sin \, \theta) r \, dz \, dr \, d\theta = \left(\int_0^{\pi/2} \sin \, \theta \, d\theta \right) \left( \int_0^2 r^2 dr\right) \left( \int_0^4 z \, dz\right) = \left(\left. -\cos \theta \right|_0^{\pi/2} \right) \left(\left.\frac{r^3}{3} \right|_0^2 \right) \left( \left. \frac{z^2}{2} \right|_0^4 \right) = \frac{64}{3}. \nonumber \]
Evaluer la triple intégrale\[\int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1} \int_{z=0}^{z=4} rz \, \sin \, \theta r \, dz \, dr \, d\theta. \nonumber \]
- Allusion
-
Suivez les mêmes étapes que dans l'exemple précédent.
- Réponse
-
\(8\)
Si la région cylindrique sur laquelle nous devons intégrer est un solide général, nous examinons les projections sur les plans de coordonnées. Ainsi, la triple intégrale d'une fonction continue\(f(r, \theta, z)\) sur une région solide générale\(E = \{(r, \theta, z)|(r, \theta) \in D, u_1 (r, \theta) \leq z \leq u_2 (r, \theta)\}\) dans\(\mathbb{R}^3\) laquelle se\(D\) trouve la\(E\) projection de sur le\(r\theta\) plan -est
\[\iiint_E f(r, \theta, z) r \, dr \, d\theta \, dz = \iint_D \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r, \theta, z) dz \right] r \, dr \, d\theta. \nonumber \]
En particulier, si\(D = \{(r, \theta) |G_1 (\theta) \leq r \leq g_2(\theta), \alpha \leq \theta \leq \beta \}\), alors nous avons
\[ \iiint_E f(r,\theta, z) r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)} \int_{z=u_1(r,\theta)}^{z=u_2(r,\theta)} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Des formules similaires existent pour les projections sur les autres plans de coordonnées. Nous pouvons utiliser les coordonnées polaires de ces plans si nécessaire.
Considérez la région\(E\) située à l'intérieur du cylindre circulaire droit avec équation\(r = 2 \, \sin \, \theta\), délimitée en bas par le\(r\theta\) plan -et délimitée au-dessus par la sphère dont le rayon est\(4\) centré sur l'origine (Figure 15.5.3). Définissez une intégrale triple sur cette région avec une fonction\(f(r, \theta, z)\) en coordonnées cylindriques.
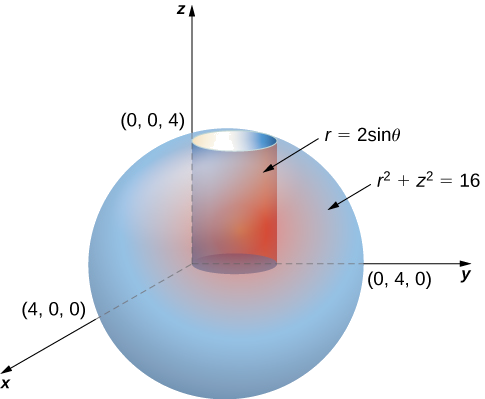
Solution
Tout d'abord, identifiez que l'équation de la sphère est\(r^2 + z^2 = 16\). Nous pouvons voir que les limites pour\(z\) sont comprises entre\(0\) et\(z = \sqrt{16 - r^2}\). Ensuite, les limites pour\(r\) sont comprises entre\(0\) et\(r = 2 \, \sin \, \theta\). Enfin, les limites pour\(\theta\) sont comprises entre\(0\) et\(\pi\). Par conséquent, la région est.\(E = \{(r,\theta, z)|0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \sin \, \theta, \, 0 \leq z \leq \sqrt{16 - r^2} \}.\) Par conséquent, la triple intégrale est
\[\iiint_E f(r,\theta, z) r \, dz \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \sin \, \theta} \int_{z=0}^{z=\sqrt{16-r^2}} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Considérez la région située à l'intérieur du cylindre circulaire droit avec une équation\(r=2 \, \sin \, \theta\) limitée en dessous par le\(r\theta\) plan -et délimitée au-dessus par\(z = 4 - y\). Définissez une intégrale triple avec une fonction\(f(r,\theta,z)\) en coordonnées cylindriques.
- Allusion
-
Analysez la région et dessinez un croquis.
- Réponse
-
\[\iiint_E f(r,\theta, z) r \, dz \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \sin \, \theta} \int_{z=0}^{z=4-r \, \sin \, \theta} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
\(E\)Soit la région délimitée en bas par le cône\(z = \sqrt{x^2 + y^2}\) et au-dessus par le paraboloïde\(z = 2 - x^2 - y^2\). (Figure 15.5.4). Définissez une intégrale triple en coordonnées cylindriques pour trouver le volume de la région, en utilisant les ordres d'intégration suivants :
un.\(dz \, dr \, d\theta\)
b.\(dr \, dz \, d\theta\)
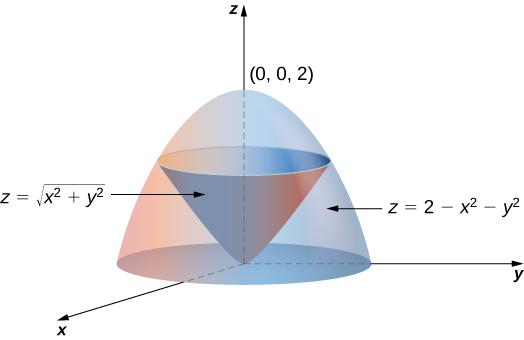
Solution
a. Le cône a un rayon 1 à l'endroit où il rencontre le paraboloïde. Depuis\(z = 2 - x^2 - y^2 = 2 - r^2\) et\(z = \sqrt{x^2 + y^2} = r^2\) (en supposant que\(r\) ce n'est pas négatif), nous avons\(2 - r^2 = r\). Résoudre, nous l'avons fait\(r^2 + r - 2 = (r + 2)(r - 1) = 0\). Depuis\(r \geq 0\), nous avons\(r = 1\). Par conséquent\(z = 1\). L'intersection de ces deux surfaces est donc un cercle de rayon\(1\) dans le plan\(z = 1\). Le cône est la limite inférieure pour\(z\) et le paraboloïde est la limite supérieure. La projection de la région sur le\(xy\) plan est le cercle de rayon\(1\) centré sur l'origine.
Ainsi, nous pouvons décrire la région comme\(E = \{(r, \theta, z) |0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 1, \, r \leq z \leq 2 - r^2 \}\).
Par conséquent, l'intégrale du volume est
\[V = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=r}^{z=2-r^2} r \, dz \, dr \, d\theta. \nonumber \]
b. On peut également écrire la surface du cône comme\(r = z\) et le paraboloïde comme\(r^2 = 2 - z\). La borne inférieure pour\(r\) est zéro, mais la limite supérieure est parfois le cône et les autres fois c'est le paraboloïde. Le plan\(z = 1\) divise la région en deux régions. La région peut alors être décrite comme\[E = \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 0 \leq z \leq 1, \, 0 \leq r \leq z\} \cup \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 1 \leq z \leq 2, \, 0 \leq r \leq \sqrt{2 - z}\}. \nonumber \]
Maintenant, l'intégrale du volume devient
\[V = \int_{\theta=0}^{\theta=2\pi} \int_{z=0}^{z=1} \int_{r=0}^{r=z} r \, dr \, dz \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{z=1}^{z=2} \int_{r=0}^{r=\sqrt{2-z}} r \, dr \, dz \, d\theta. \nonumber \]
Refaites l'exemple précédent avec l'ordre d'intégration\(d\theta \, dz \, dr\).
- Allusion
-
Notez que\(\theta\) c'est indépendant de\(r\) et\(z\).
- Réponse
-
\(E = \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 0 \leq z \leq 1, \, 0 \leq r \leq 2 - z^2\}\)et\[V = \int_{r=0}^{r=1} \int_{z=0}^{z=2 - r^2} \int_{\theta=0}^{\theta=2\pi} r \, d\theta \, dz \, dr. \nonumber \]
Solution
a. Notez que l'équation de la sphère est
\[x^2 + y^2 + z^2 = 4 \, \text{or} \, r^2 + z^2 = 4 \nonumber \]
et l'équation pour le cylindre est
\[x^2 + y^2 = 1 \, \text{or} \, r^2 = 1. \nonumber \]
Ainsi, nous avons pour la région\(E\)
\[E = \{(r,\theta,z)|0 \leq z \leq \sqrt{4 - r^2}, \, 0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\} \nonumber \]
Par conséquent, l'intégrale du volume est
\[\begin{align} V (E) = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=0}^{z=\sqrt{4-r^2}} r \, dz \, dr \, d\theta \\ = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left[ \left>rz\right|_{z=0}^{z=\sqrt{4-r^2}}\right] dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left(r\sqrt{4 - r^2}\right) dr \, d\theta\\ = \int_0^{2\pi} \left(\frac{8}{3} - \sqrt{3} \right) d\theta = 2\pi \left(\frac{8}{3} - \sqrt{3} \right) \, \text{cubic units.} \end{align} \nonumber \]
b. Puisque la sphère est\(x^2 + y^2 + z^2 = 4\), qui est\(r^2 + z^2 = 4\), et que le cylindre est\(x^2 + y^2 = 1\), ce qui est\(r^2 = 1\), nous avons\(1 + z^2 = 4\), c'est-à-dire\(z^2 = 3\). Nous avons donc deux régions, puisque la sphère et le cylindre se croisent\((1,\sqrt{3})\) dans le\(rz\) plan
\[E_1 = \{ (r,\theta,z) | 0 \leq r \leq \sqrt{4 - r^2}, \, \sqrt{3} \leq z \leq 2, \, 0 \leq \theta \leq 2\pi\} \nonumber \]et
\[E_2 = \{(r,\theta,z) | 0 \leq r \leq 1, \, 0 \leq z \leq \sqrt{3}, \, 0 \leq \theta \leq 2\pi\}. \nonumber \]
Par conséquent, l'intégrale du volume est
\[\begin{align} V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{z=\sqrt{3}}^{z=2} \int_{r=0}^{r=\sqrt{4-r^2}} r \, dr \, dz \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{z=0}^{z=\sqrt{3}} \int_{r=0}^{r=1} r \, dr \, dz \, d\theta\\ = \sqrt{3} \pi + \left( \dfrac{16}{3} - 3 \sqrt{3} \right) \pi = 2\pi \left( \frac{8}{3} - \sqrt{3} \right) \, \text{cubic units.} \end{align} \nonumber \]
Refaites l'exemple précédent avec l'ordre d'intégration\(d\theta \, dz \, dr\).
- Allusion
-
Un chiffre peut être utile. Notez que\(\theta\) c'est indépendant de\(r\) et\(z\).
- Réponse
-
\(E_2 = \{(r,\theta,z) | 0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 1, \, r \leq z \leq \sqrt{4 - r^2}\}\)et
\[V = \int_{r=0}^{r=1} \int_{z=r}^{z=\sqrt{4-r^2}} \int_{\theta=0}^{\theta=2\pi} r \, d\theta \, dz \, dr. \nonumber \]
Révision des coordonnées sphériques
\(\mathbb{R}^3\)Dans l'espace tridimensionnel du système de coordonnées sphériques, nous spécifions un point\(P\) en fonction de sa\(\rho\) distance par rapport à l'origine,\(\theta\) de l'angle polaire par rapport à\(x\) l'axe positif (comme dans le système de coordonnées cylindriques) et\(\varphi\) de l'angle par rapport au positif \(z\)-axe et ligne\(OP\) (Figure\(\PageIndex{6}\)). Notez que\(\rho > 0\) et\(0 \leq \varphi \leq \pi\). (Reportez-vous à la section Coordonnées cylindriques et sphériques pour un examen.) Les coordonnées sphériques sont utiles pour les intégrales triples sur des régions symétriques par rapport à l'origine.
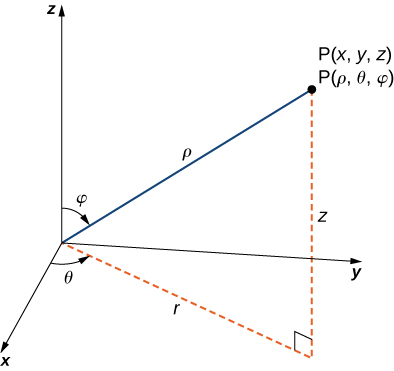
Rappelez les relations qui relient les coordonnées rectangulaires aux coordonnées sphériques.
Des coordonnées sphériques aux coordonnées rectangulaires :
\[x = \rho \, \sin \, \varphi \, \cos \theta, \, y = \rho \, \sin \, \varphi \, \sin \, \theta, \, and \, z = \rho \, \cos \, \varphi. \nonumber \]
Des coordonnées rectangulaires aux coordonnées sphériques :
\[\rho^2 = x^2 + y^2 + z^2, \, \tan \, \theta = \frac{y}{x}, \, \varphi = \arccos \left( \frac{z}{\sqrt{x^2 + y^2 + z^2}}\right). \nonumber \]
Les autres relations qu'il est important de connaître pour les conversions sont
- \(r = \rho \, \sin \, \varphi\)
- \(\theta = \theta\)Ces équations sont utilisées pour convertir des coordonnées sphériques en coordonnées cylindriques.
- \(z = \rho \, \cos \, \varphi\)
et
- \(\rho = \sqrt{r^2 + z^2}\)
- \(\theta = \theta\)Ces équations sont utilisées pour convertir des coordonnées cylindriques en coordonnées sphériques.
- \(\varphi = \arccos \left(\frac{z}{\sqrt{r^2 + z^2}}\right)\)
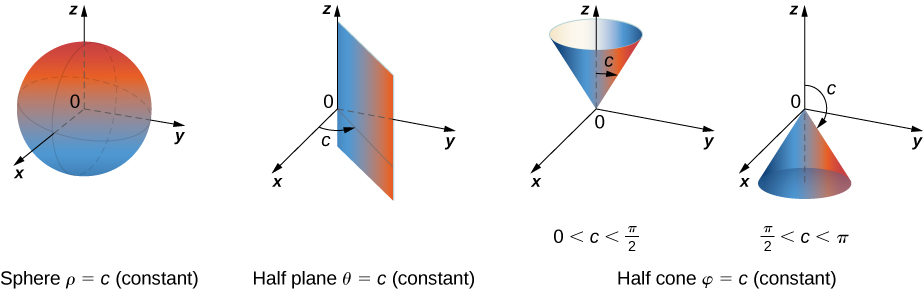
\(\PageIndex{7}\)montre quelques régions solides qu'il est pratique d'exprimer en coordonnées sphériques.
Intégration dans les coordonnées sphériques
Nous établissons maintenant une triple intégrale dans le système de coordonnées sphériques, comme nous le faisions auparavant dans le système de coordonnées cylindriques. Laissez la fonction\(f(\rho,\theta,\varphi)\) être continue dans une boîte sphérique bornée,\(B = \{(\rho,\theta,\varphi) | a \leq \rho \leq b, \, \alpha \leq \theta \leq \beta, \, \gamma \leq \varphi \leq \psi \}\). Nous divisons ensuite chaque intervalle en\(l,m,n\)\(n\) subdivisions de telle sorte que\(\Delta \rho = \frac{b - a}{l}, \, \Delta \theta = \frac{\beta - \alpha}{m}. \, \Delta \varphi = \frac{\psi - \gamma}{n}\). Nous pouvons maintenant illustrer le théorème suivant pour les intégrales triples en coordonnées sphériques avec\((\rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*)\) n'importe quel point d'échantillonnage dans la sous-boîte sphérique\(B_{ijk}\). Pour l'élément de volume de la sous-boîte\(\Delta V\) en coordonnées sphériques, nous avons\(\Delta V = (\Delta \rho)\, (\rho \Delta \varphi)\, (\rho \, \sin \, \varphi \, \Delta \theta)\), comme indiqué dans la figure suivante.
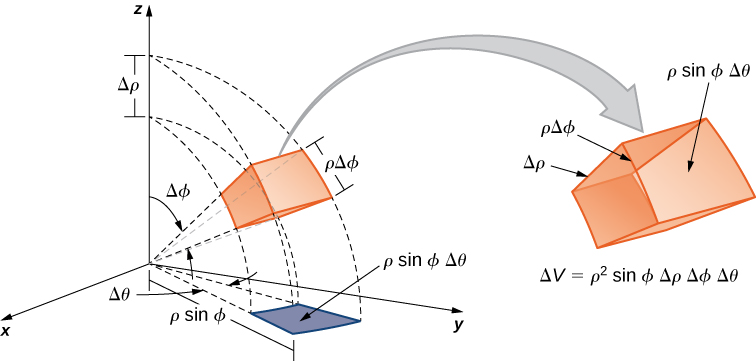
La triple intégrale en coordonnées sphériques est la limite d'une triple somme de Riemann,
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( \rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*) (\rho_{ijk}^*)^2 \sin \, \varphi \Delta \rho \Delta \theta \Delta \varphi \nonumber \]
à condition que la limite existe.
Comme pour les autres intégrales multiples que nous avons examinées, toutes les propriétés fonctionnent de la même manière pour une intégrale triple dans le système de coordonnées sphériques, de même que les intégrales itérées. Le théorème de Fubini prend la forme suivante.
S'il\(f(\rho,\theta, \varphi)\) est continu sur une boîte solide sphérique\(B = [a,b] \times [\alpha,\beta] \times [\gamma , \psi]\), alors
\[\iiint_B f(\rho,\theta,\varphi ) \, \rho^2 \sin \, \varphi d\rho \, d\varphi \, d\theta = \int_{\varphi=\gamma}^{\varphi=\psi} \int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=a}^{\rho=b} f(\rho,\theta,\varphi) \, \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Cette intégrale itérée peut être remplacée par d'autres intégrales itérées par intégration par rapport aux trois variables dans d'autres ordres.
Comme indiqué précédemment, les systèmes de coordonnées sphériques fonctionnent bien pour les solides symétriques autour d'un point, tels que les sphères et les cônes. Examinons quelques exemples avant de considérer les intégrales triples en coordonnées sphériques sur des régions sphériques générales.
Evaluer la triple intégrale itérée
\[\int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/2} \int_{\rho=0}^{\rho=1} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Solution
Comme précédemment, dans ce cas, les variables de l'intégrale itérée sont en fait indépendantes les unes des autres et nous pouvons donc intégrer chaque élément et les multiplier :
\[\int_0^{2\pi} \int_0^{\pi/2} \int_0^1 \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta = \int_0^{2\pi} d\theta \int_0^{\pi/2} \sin \, \varphi \, d\varphi \int_0^1 \rho^2 d\rho = (2\pi) \, (1) \, \left(\frac{1}{3}\right) = \frac{2\pi}{3} \nonumber \]
Le concept de triple intégration en coordonnées sphériques peut être étendu à l'intégration sur un solide général, en utilisant les projections sur les plans de coordonnées. Notez cela\(dV\) et\(dA\) signifiez les incréments de volume et de surface, respectivement. Les variables\(V\) et\(A\) sont utilisées comme variables d'intégration pour exprimer les intégrales.
Intégrale triple d'une fonction continue\(f(\rho,\theta,\varphi)\) sur une région solide générale
\[E = \{(\rho,\theta,\varphi) |(\rho,\theta) \in D, u_1 (\rho, \theta) \leq \varphi \leq u_2 (\rho,\theta)\} \nonumber \]
dans\(\mathbb{R}^3\), où\(D\) est la projection de\(E\) sur le\(\rho \theta\) plan -plane, est
\[\iiint_E f(\rho, \theta,\varphi) dV = \iint_D \left[ \int_{u_1(\rho,\theta)}^{u_2(\rho,\theta)} f(\rho,\theta,\varphi) \, d\varphi \right] \, dA. \nonumber \]
En particulier, si\(D = \{(\rho,\theta) | g_1 (\theta) \leq \rho \leq g_2 (\theta), \, \alpha \leq \theta \leq \beta\}\), le nous avons
\[\iiint_E f(\rho,\theta,\varphi) dV = \int_{\alpha}^{\beta} \int_{g_1(\theta)}^{g_2(\theta)} \int_{u_1(\rho,\theta)}^{u_2(\rho,\theta)} f(\rho,\theta,\varphi ) \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta. \nonumber \]
Des formules similaires s'appliquent aux projections sur les autres plans de coordonnées.
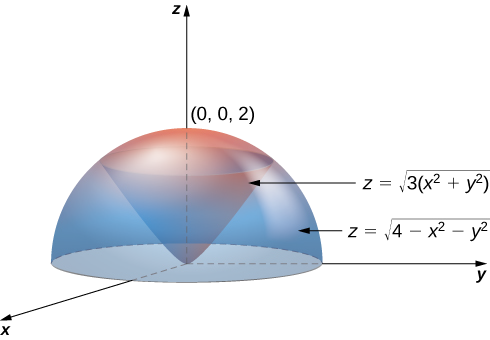
Établissez une intégrale pour le volume de la région délimitée par le cône\(z = \sqrt{3(x^2 + y^2)}\) et l'hémisphère\(z = \sqrt{4 - x^2 - y^2}\) (voir la figure ci-dessous).
Solution
En utilisant les formules de conversion des coordonnées rectangulaires en coordonnées sphériques, nous avons :
Pour le cône :\(z = \sqrt{3(x^2 + y^2)}\) ou\(\rho \, \cos \, \varphi = \sqrt{3} \rho \, \sin \, \varphi\) ou\(\tan \, \varphi = \frac{1}{\sqrt{3}}\) ou\(\varphi = \frac{\pi}{6}\).
Pour la sphère :\(z = \sqrt{4 - x^2 - y^2}\) ou\(z^2 + x^2 + y^2 = 4\) ou\(\rho^2 = 4\) ou\(\rho = 2\).
Ainsi, l'intégrale triple du volume est
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi+\pi/6} \int_{\rho=0}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Établissez une intégrale triple pour le volume de la région solide délimitée au-dessus par la sphère\(\rho = 2\) et limitée en dessous par le cône\(\varphi = \pi/3\).
- Allusion
-
Suivez les étapes de l'exemple précédent.
- Réponse
-
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/3} \int_{\rho=0}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta \nonumber \]
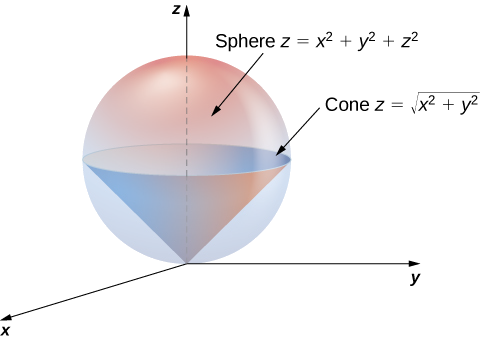
\(E\)Soit la région délimitée en bas par le cône\(z = \sqrt{x^2 + y^2}\) et au-dessus par la sphère\(z = x^2 + y^2 + z^2\) (Figure 15.5.10). Définissez une triple intégrale en coordonnées sphériques et déterminez le volume de la région en utilisant les ordres d'intégration suivants :
- \(d\rho \, d\phi \, d\theta\)
- \(d\varphi \, d\rho \, d\theta\)
Solution
a. Utilisez les formules de conversion pour écrire les équations de la sphère et du cône en coordonnées sphériques.
Pour la sphère :
\[\begin{align} x^2 + y^2 + z^2 = z \\\rho^2 = \rho \, \cos \, \varphi \\\rho = \cos \, \varphi. \end{align} \nonumber \]
Pour le cône :
\[\begin{align} z = \sqrt{x^2 + y^2}\\\rho \, \cos \, \varphi = \sqrt{\rho^2 \sin^2 \, \varphi \, \cos^2 \phi } \\ \rho \, \cos \, \varphi = \sqrt{\rho^2 \sin^2 \varphi \, (\cos^2\phi + \sin^2 \phi)}\\ \rho \, \cos \, \varphi = \rho \, \sin \, \varphi\\ \cos \, \varphi = \sin \, \varphi\\ \varphi = \pi/4. \end{align} \nonumber \]
Ainsi, l'intégrale du volume de la région solide\(E\) devient
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/4} \int_{\rho=0}^{\rho=\cos \, \varphi} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
b. Considérez le\(\varphi\rho\) plan. Notez que les plages pour\(\varphi\) et\(\rho\) (à partir de la partie a.) sont
\[\begin{align} 0\leq \rho \sqrt{2}/2 \text{and}\, \sqrt{2} \leq \rho 1 \\ 0 \leq \varphi \leq \pi/4 0 \leq \rho \leq \cos \, \varphi \end{align} \nonumber \]
La courbe\(\rho = \cos \, \varphi\) rejoint la droite\(\varphi = \pi/4\) au point\((\pi/4,\sqrt{2}/2)\). Ainsi, pour modifier l'ordre d'intégration, nous devons utiliser deux éléments :
\[0 \leq \rho \leq \sqrt{2}/2, \, 0 \leq \varphi \leq \pi/4 \nonumber \]et
\[\sqrt{2}/2 \leq \rho \leq 1, \, 0 \leq \varphi \leq \cos^{-1} \rho. \nonumber \]
Ainsi, l'intégrale du volume de la région solide\(E\) devient
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\rho=0}^{\rho=\sqrt{2}/2} \int_{\varphi=0}^{\varphi=\pi/4} \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\sqrt{2}/2}^{\rho=1} \int_{\varphi=0}^{\varphi=\cos^{-1}\rho} \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta \nonumber \]
Dans chaque cas, l'intégration aboutit à\(V(E) = \frac{\pi}{8}\).
Avant de terminer cette section, nous présentons quelques exemples qui peuvent illustrer la conversion de coordonnées rectangulaires en coordonnées cylindriques et de coordonnées rectangulaires en coordonnées sphériques.
Convertissez l'intégrale suivante en coordonnées cylindriques :
\[\int_{y=-1}^{y=1} \int_{x=0}^{x=\sqrt{1-y^2}} \int_{z=x^2+y^2}^{z=\sqrt{x^2+y^2}} xyz \, dz \, dx \, dy. \nonumber \]
Solution
Les plages des variables sont
\[\begin{align} -1 \leq y \leq y \\ 0 \leq x \leq \sqrt{1 - y^2} \\x^2 + y^2 \leq z \leq \sqrt{x^2 + y^2}. \end{align} \nonumber \]
Les deux premières inégalités décrivent la moitié droite d'un cercle de rayon\(1\). Par conséquent, les plages pour\(\theta\) et\(r\) sont
\[-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \, \text{and} \, 0 \leq r \leq 1. \nonumber \]
Les limites de\(z\) sont\(r^2 \leq z \leq r\) donc
\[\int_{y=-1}^{y=1} \int_{x=0}^{x=\sqrt{1-y^2}} \int_{z=x^2+y^2}^{z=\sqrt{x^2+y^2}} xyz \, dz \, dx \, dy = \int_{\theta=-\pi/2}^{\theta=\pi/2} \int_{r=0}^{r=1} \int_{z=r^2}^{z=r} r(r \, \cos \theta) \, (r \, \sin \, \theta) \, z \, dz \, dr \, d\theta. \nonumber \]
Convertissez l'intégrale suivante en coordonnées sphériques :
\[\int_{y=0}^{y=3} \int_{x=0}^{x=\sqrt{9-y^2}} \int_{z=\sqrt{x^2+y^2}}^{z=\sqrt{18-x^2-y^2}} (x^2 + y^2 + z^2) dz \, dx \, dy. \nonumber \]
Solution
Les plages des variables sont
\[\begin{align} 0 \leq y \leq 3\\ 0 \leq x \leq \sqrt{9 - y^2} \\ \sqrt{x^2 + y^2} \leq z \leq \sqrt{18 - x^2 - y^2}. \end{align} \nonumber \]
Les deux premières plages de variables décrivent un quart de disque dans le premier quadrant du\(xy\) plan. D'où la gamme pour\(\theta\) is\(0 \leq \theta \leq \frac{\pi}{2}\).
La limite inférieure\(z = \sqrt{x^2 + y^2}\) est la moitié supérieure d'un cône et la limite supérieure\(z = \sqrt{18 - x^2 - y^2}\) est la moitié supérieure d'une sphère. Par conséquent, nous avons\(0 \leq \rho \leq \sqrt{18}\), ce qui est\(0 \leq \rho \leq 3\sqrt{2}\).
Pour les plages de,\(\varphi\) nous devons trouver où le cône et la sphère se croisent, donc résolvez l'équation
\[\begin{align} r^2 + z^2 = 18\\(\sqrt{x^2 + y^2})^2 + z^2 = 18 \\z^2 + z^2 = 18 \\2z^2 = 18 \\z^2 = 9 \\z = 3. \end{align} \nonumber \]
Cela donne
\[\begin{align} 3\sqrt{2} \, \cos \, \varphi = 3 \\\cos \, \varphi = \frac{1}{\sqrt{2}} \\\varphi = \frac{\pi}{4}. \end{align} \nonumber \]
En mettant tout cela ensemble, nous obtenons
\[\int_{y=0}^{y=3} \int_{x=0}^{x=\sqrt{9-y^2}} \int_{z=\sqrt{x^2+y^2}}^{z=\sqrt{18-x^2-y^2}} (x^2 + y^2 + z^2) dz \, dx \, dy = \int_{\varphi=0}^{\varphi=\pi/4} \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=3\sqrt{2}} \rho^4 \sin \, \varphi \, d\rho \, d\theta \, d\varphi. \nonumber \]
Utilisez des coordonnées rectangulaires, cylindriques et sphériques pour définir des intégrales triples afin de déterminer le volume de la région à l'intérieur de la sphère\(x^2 + y^2 + z^2 = 4\) mais à l'extérieur du cylindre\(x^2 + y^2 = 1\).
- Réponse : Rectangulaire
-
\[\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} \int_{z=-\sqrt{4-x^2-y^2}}^{z=\sqrt{4-x^2-y^2}} dz \, dy \, dx - \int_{x=-1}^{x=1} \int_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}} \int_{z=-\sqrt{4-x^2-y^2}}^{z=\sqrt{4-x^2-y^2}} dz \, dy \, dx. \nonumber \]
- Réponse : cylindrique
-
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=1}^{r=2} \int_{z=-\sqrt{4-r^2}}^{z=\sqrt{4-r^2}} r \, dz \, dr \, d\theta. \nonumber \]
- Réponse : Sphérique
-
\[\int_{\varphi=\pi/6}^{\varphi=5\pi/6} \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\csc \, \varphi}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\theta \, d\varphi. \nonumber \]
Maintenant que nous connaissons le système de coordonnées sphériques, découvrons le volume de certaines figures géométriques connues, telles que les sphères et les ellipsoïdes.
Trouvez le volume du planétarium sphérique de L'Hemisphèric à Valence, en Espagne, qui mesure cinq étages et a un rayon d'environ\(50\) pieds, à l'aide de l'équation\(x^2 + y^2 + z^2 = r^2\).

Solution
Nous calculons le volume de la balle dans le premier octant, où et\(x \leq 0, \, y \leq 0\)\(z \leq 0\), en utilisant des coordonnées sphériques, puis nous multiplions le résultat par\(8\) pour la symétrie. Puisque nous considérons la région\(D\) comme le premier octant de l'intégrale, les plages des variables sont
\[0 \leq \varphi \leq \frac{\pi}{2}, \, 0 \leq \rho \leq r, \, 0 \leq \theta \leq \frac{\pi}{2}. \nonumber \]
Par conséquent,
\[\begin{align} V = \iiint_D dx \, dy \, dz = 8 \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=\pi} \int_{\varphi=0}^{\varphi=\pi/2} \rho^2 \sin \, \theta \, d\varphi \, d\rho \, d\varphi \\ =8 \int_{\varphi=0}^{\varphi=\pi/2} d\varphi \int_{\rho=0}^{\rho=r} \rho^2 d\rho \int_{\theta=0}^{\theta=\pi/2} \sin \, \theta \, d\theta \\ = 8 \, \left(\frac{\pi}{2}\right) \, \left( \frac{r^3}{3} \right) \, (1) \\ =\dfrac{4}{3} \pi r^3.\end{align} \nonumber \]
Cela correspond exactement à ce que nous savions. Donc, pour une sphère avec un rayon d'environ\(50\) pieds, le volume est\(\frac{4}{3} \pi (50)^3 \approx 523,600 \, ft^3\).
Pour l'exemple suivant, nous trouvons le volume d'un ellipsoïde.
Détermine le volume de l'ellipsoïde\(\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1\).
Solution
Nous utilisons à nouveau la symétrie et évaluons le volume de l'ellipsoïde à l'aide de coordonnées sphériques. Comme précédemment, nous utilisons le premier octant\(x \leq 0, \, y \leq 0\),\(z \leq 0\) puis nous multiplions le résultat par\(8\).
Dans ce cas, les plages des variables sont
\[0 \leq \varphi \leq \frac{\pi}{2} \, 0 \leq \rho \leq 1, \, \text{and} \, 0 \leq \theta \leq \frac{\pi}{2}. \nonumber \]
De plus, nous devons changer les coordonnées rectangulaires en coordonnées sphériques de cette manière :
\[x = a \rho \, \cos \, \varphi \, \sin \, \theta, \, y = b\rho \, \sin \, \varphi \, \sin \, \theta, \, \text{and} \, z = cp \, \cos \theta. \nonumber \]
Ensuite, le volume de l'ellipsoïde devient
\[\begin{align} V = \iiint_D dx \, dy \, dz \\ = 8 \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=1} \int_{\varphi=0}^{\varphi=\pi/2} abc \, \rho^2 \sin \, \theta \, d\varphi \, d\rho \, d\theta \\ \\ = 8abc \int_{\varphi=0}^{\varphi=\pi/2} d\varphi \int_{\rho=0}^{\rho=1} \rho^2 d\rho \int_{\theta=0}^{\theta=\pi/2} \sin \, \theta \, d\theta \\ = 8abc \left(\frac{\pi}{2}\right) \left( \frac{1}{3}\right) (1) \\ = \frac{4}{3} \pi abc. \end{align} \nonumber \]
Déterminez le volume de l'espace à l'intérieur de l'ellipsoïde\(\frac{x^2}{75^2} + \frac{y^2}{80^2} + \frac{z^2}{90^2} = 1\) et à l'extérieur de la sphère\(x^2 + y^2 + z^2 = 50^2\).
Solution
Ce problème est directement lié à la structure de l'hémisphère. Le volume d'espace à l'intérieur de l'ellipsoïde et à l'extérieur de la sphère peut être utile pour déterminer le coût du chauffage ou du refroidissement de cet espace. Nous pouvons utiliser les deux exemples précédents pour le volume de la sphère et de l'ellipsoïde, puis soustraire.
Nous trouvons d'abord le volume de l'ellipsoïde en utilisant\(a = 75\) ft,\(b = 80\) ft et\(c = 90\) ft dans le résultat de l'exemple. Le volume de l'ellipsoïde est donc
\[V_{ellipsoid} = \frac{4}{3} \pi (75)(80)(90) \approx 2,262,000 \, ft^3. \nonumber \]
À partir de l'exemple, le volume de la sphère est
\[V_{sphere} \approx 523,600 \, ft^3. \nonumber \]
Par conséquent, le volume de l'espace à l'intérieur de l'ellipsoïde\(\frac{x^2}{75^2} + \frac{y^2}{80^2} + \frac{z^2}{90^2} = 1\) et à l'extérieur de la sphère\(x^2 + y^2 + z^2 = 50^2\) est d'environ
\[V_{Hemispheric} = V_{ellipsoid} - V_{sphere} = 1,738,400 \, ft^3. \nonumber \]
La montgolfière est un passe-temps relaxant et paisible que beaucoup de gens apprécient. De nombreux rassemblements de montgolfières ont lieu dans le monde entier, comme l'Albuquerque International Balloon Fiesta. L'événement d'Albuquerque est le plus grand festival de montgolfières au monde, avec plus de\(500\) ballons participants chaque année.

Comme leur nom l'indique, les montgolfières utilisent l'air chaud pour générer de la portance. (L'air chaud étant moins dense que l'air froid, le ballon flotte tant que l'air chaud reste chaud.) La chaleur est générée par un brûleur à propane suspendu sous l'ouverture du panier. Une fois que le ballon a décollé, le pilote contrôle l'altitude du ballon, soit en utilisant le brûleur pour chauffer l'air et monter, soit en utilisant un évent situé près du sommet du ballon pour libérer l'air chaud et descendre. Le pilote a toutefois très peu de contrôle sur l'orientation du ballon, car les ballons sont à la merci des vents. L'incertitude quant à notre destination est l'une des raisons pour lesquelles les aérostistes sont attirés par ce sport.
Dans ce projet, nous utilisons des intégrales triples pour en savoir plus sur les montgolfières. Nous modélisons le ballon en deux pièces. Le sommet du ballon est modélisé par une demi-sphère de rayon 28
pieds. Le bas du ballon est modelé par un tronc de cône (imaginez un cornet de crème glacée dont l'extrémité pointue est coupée). Le rayon de la grande extrémité du tronc est en\(28\) pieds et le rayon de la petite extrémité du tronc est en\(28\) pieds. Un graphique de notre modèle de ballon et un diagramme en coupe montrant les dimensions sont présentés dans la figure suivante.
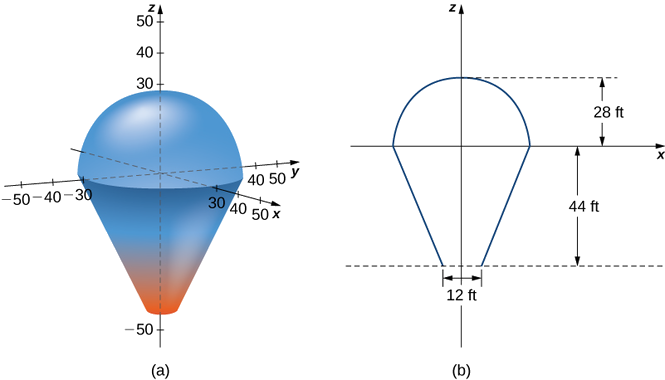
Nous voulons d'abord connaître le volume du ballon. Si nous examinons séparément la partie supérieure et la partie inférieure du ballon, nous constatons qu'il s'agit de solides géométriques avec des formules de volume connues. Cependant, il est toujours intéressant de configurer et d'évaluer les intégrales dont nous aurions besoin pour trouver le volume. Si nous calculons le volume par intégration, nous pouvons utiliser les formules de volume connues pour vérifier nos réponses. Cela nous permettra de nous assurer que les intégrales sont correctement configurées pour les étapes ultérieures et plus complexes du projet.
1. Trouvez le volume du ballon de deux manières.
a. Utilisez des intégrales triples pour calculer le volume. Examinez chaque partie du ballon séparément. (Envisagez d'utiliser des coordonnées sphériques pour la partie supérieure et des coordonnées cylindriques pour la partie inférieure.)
b. Vérifiez la réponse à l'aide des formules pour le volume d'une sphère et pour le volume d'un cône,\(V = \frac{1}{3} \pi r^2 h\).\(V = \frac{4}{3}\pi r^3\)
En réalité, le calcul de la température à un point situé à l'intérieur du ballon est une tâche extrêmement complexe. En fait, toute une branche de la physique (la thermodynamique) est consacrée à l'étude de la chaleur et de la température. Pour les besoins de ce projet, nous allons toutefois émettre quelques hypothèses simplificatrices sur la façon dont la température varie d'un point à l'autre à l'intérieur du ballon. Supposons que juste avant le décollage, la température (en degrés Fahrenheit) de l'air à l'intérieur du ballon varie en fonction de la fonction\[T_0 (r,\theta,z) = \frac{z - r}{10} + 210. \nonumber \]
2. Quelle est la température moyenne de l'air dans le ballon juste avant le décollage ? (Encore une fois, regardez chaque partie de la bulle séparément et n'oubliez pas de convertir la fonction en coordonnées sphériques lorsque vous regardez la partie supérieure de la bulle.)
Maintenant, le pilote active le brûleur pendant\(10\) quelques secondes. Cette action affecte la température dans une colonne\(12\) d'un pied de largeur de\(20\) pieds de haut, directement au-dessus du brûleur. Une coupe transversale du ballon représentant cette colonne est illustrée dans la figure suivante
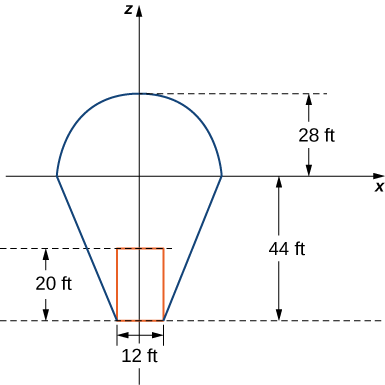
Supposons qu'après que le pilote active le brûleur pendant\(10\) quelques secondes, la température de l'air dans la colonne décrite ci-dessus augmente selon la formule
\[H(r,\theta,z) = -2z - 48. \nonumber \]
Ensuite, la température de l'air dans la colonne est donnée par\[T_1(r,\theta,z) = \frac{z - r}{10} + 210 + (-2z - 48), \nonumber \]
tandis que la température dans le reste du ballon est toujours donnée par\[T_0(r,\theta,z) = \frac{z - r}{10} + 210. \nonumber \]
3. Déterminez la température moyenne de l'air dans le ballon une fois que le pilote a activé le brûleur pendant\(10\) quelques secondes.
Concepts clés
- Pour évaluer une intégrale triple en coordonnées cylindriques, utilisez l'intégrale itérée\[\int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)} \int_{z=u_1(r,\theta)}^{u_2(r,\theta)} f(r,\theta,z)r \, dz \, dr \, d\theta. \nonumber \nonumber \]
- Pour évaluer une triple intégrale en coordonnées sphériques, utilisez l'intégrale itérée\[\int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=g_1(\theta)}^{\rho=g_2(\theta)} \int_{\varphi=u_1(r,\theta)}^{u_2(r,\theta)} f(\rho,\theta,\varphi) \, \rho^2 \sin \varphi \, d\varphi \, d\rho \, d\theta. \nonumber \nonumber \]
Équations clés
- Intégrale triple en coordonnées cylindriques\[\iiint_B g(s,y,z)dV = \iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz = \iiint_B f(r,\theta,z) r \, dr \, d\theta \, dz \nonumber \]
- Intégrale triple en coordonnées sphériques\[\iiint_B f(\rho,\theta,\varphi) \rho^2 \sin \varphi \, d\rho \, d\varphi \, d\theta = \int_{\varphi=\gamma}^{\varphi=\psi} \int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=a}^{\rho=b} f(\rho, \theta, \varphi) \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta\nonumber \]
Lexique
- intégrale triple en coordonnées cylindriques
-
la limite d'une triple somme de Riemann, à condition que la limite suivante existe :
\[lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(r_{ijk}^*, \theta_{ijk}^*, s_{ijk}^*) r_{ijk}^* \Delta r \Delta \theta \Delta z \nonumber \]
- intégrale triple en coordonnées sphériques
-
la limite d'une triple somme de Riemann, à condition que la limite suivante existe :
\[lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*) (\rho_{ijk}^*)^2 \sin \, \varphi \Delta \rho \Delta \theta \Delta \varphi \nonumber \]



Soit E la région délimitée en bas par le\(r\theta\) plan, au-dessus par la sphère\(x^2 + y^2 + z^2 = 4\) et sur les côtés par le cylindre\(x^2 + y^2 = 1\) (Figure 15.5.5). Définissez une intégrale triple en coordonnées cylindriques pour trouver le volume de la région en utilisant les ordres d'intégration suivants, et dans chaque cas, trouvez le volume et vérifiez que les réponses sont les mêmes :