Skip to main content
Global

15.5E : Exercices pour la section 15.5

  1. Last updated
  2. Save as PDF
  • Page ID
    197501

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 8, évaluez les intégrales triples\(\displaystyle \iiint_E f(x,y,z) \, dV\) par rapport au solide\(E\).

    1. \(f(x,y,z) = z, \quad B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 9, \quad x \leq 0, \quad y \leq 0, \quad 0 \leq z \leq 1\big\}\)

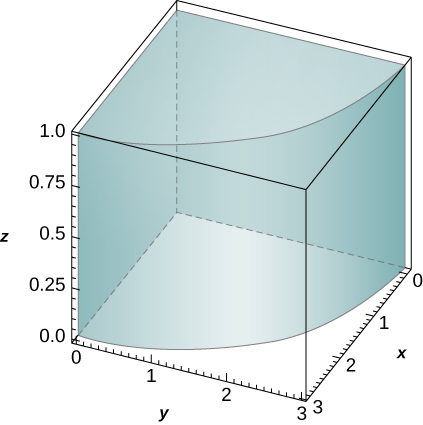
    Un quart de section d'un cylindre de hauteur 1 et de rayon 3.

    Réponse
    \(\frac{9\pi}{8}\)

    2. \(f(x,y,z) = xz^2, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 16, \space x \geq 0, \space y \leq 0, \space -1 \leq z \leq 1\big\}\)

    3. \(f(x,y,z) = xy, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 1, \space x \geq 0, \space x \geq y, \space -1 \leq z \leq 1\big\}\)

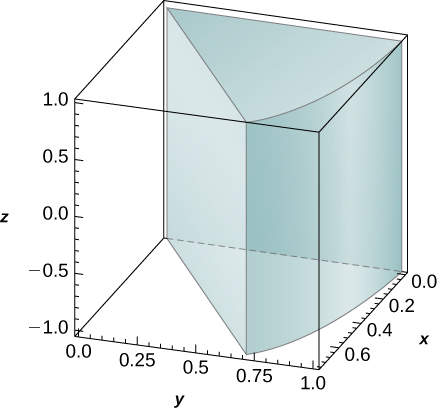
    A wedge with radius 1, height 1, and angle pi/4.

    Réponse
    \(\frac{1}{8}\)

    4. \(f(x,y,z) = x^2 + y^2, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 4, \space x \geq 0, \space x \leq y, \space 0 \leq z \leq 3\big\}\)

    5. \(f(x,y,z) = e^{\sqrt{x^2+y^2}}, \space B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 4, \space y \leq 0, \space x \leq y\sqrt{3}, \space 2 \leq z \leq 3 \big\}\)

    Réponse
    \(\frac{\pi e^2}{6}\)

    6. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 9, \space y \leq 0, \space 0 \leq z \leq 1\big\}\)

    7. a.\(B\) Soit une coque cylindrique avec un rayon intérieur\(b\), un rayon\(a\) extérieur et une hauteur\(c\) où\(0 < a < b\) et\(c>0\). Supposons qu'une fonction\(F\) définie sur\(B\) puisse être exprimée en coordonnées cylindriques sous la forme de fonctions\(h\) dérivables\(F(x,y,z) = f(r) + h(z)\), où\(f\) et sous forme de fonctions dérivables. Si\(\displaystyle \int_a^b \bar{f} (r) \,dr = 0\) et\(\bar{h}(0) = 0\), où\(\bar{f}\) et\(\bar{h}\) sont des antidérivés de\(f\) et\(h\), respectivement, montrent que\(\displaystyle \iiint_B F(x,y,z) \,dV = 2\pi c (b\bar{f} (b) - a \bar{f}(a)) + \pi(b^2 - a^2) \bar{h} (c).\)

    b. Utilisez le résultat précédent pour montrer\( \displaystyle \iiint_B \left(z + \sin \sqrt{x^2 + y^2}\right) \,dx \space dy \space dz = 6 \pi^2 ( \pi - 2),\) où se\(B\) trouve une coque cylindrique avec un rayon intérieur\(2\pi\), un rayon\(\pi\) extérieur et une hauteur\(2\).

    8. a.\(B\) Soit une coque cylindrique avec un rayon intérieur, un rayon\(a\) extérieur\(b\) et une hauteur\(c\) où\(0 < a < b\) et\(c > 0\). Supposons qu'une fonction\(F\) définie sur\(B\) puisse être exprimée en coordonnées cylindriques sous la forme de fonctions\(h\) dérivables\(F(x,y,z) = f(r) g(\theta) f(z)\), où\(f, \space g,\) et sous forme de fonctions dérivables. Si\(\displaystyle\int_a^b \tilde{f} (r) \, dr = 0,\) où\(\tilde{f}\) est un antidérivé de\(f\), montrez que\(\displaystyle\iiint_B F (x,y,z)\,dV = [b\tilde{f}(b) - a\tilde{f}(a)] [\tilde{g}(2\pi) - \tilde{g}(0)] [\tilde{h}(c) - \tilde{h}(0)],\) où\(\tilde{g}\) et\(\tilde{h}\) sont des antidérivés de\(g\) et\(h\), respectivement.

    b. Utilisez le résultat précédent pour montrer\(\displaystyle\iiint_B z \sin \sqrt{x^2 + y^2} \,dx \space dy \space dz = - 12 \pi^2,\) où se\(B\) trouve une coque cylindrique avec un rayon intérieur\(2\pi\), un rayon\(\pi\) extérieur et une hauteur\(2\).

    Dans les exercices 9 à 12, les limites du solide\(E\) sont données en coordonnées cylindriques.

    a. Exprime la région\(E\) en coordonnées cylindriques.

    b. Convertissez l'intégrale\(\displaystyle \iiint_E f(x,y,z) \,dV\) en coordonnées cylindriques.

    9. \(E\)est délimité par le cylindre circulaire droit\(r = 4 \sin \theta\), le\(r\theta\) plan et la sphère\(r^2 + z^2 = 16\).

    Réponse

    un.\(E = \big\{(r,\theta,z)\, | \,0 \leq \theta \leq \pi, \space 0 \leq r \leq 4 \sin \theta, \space 0 \leq z \leq \sqrt{16 - r^2}\big\}\)

    b.\(\displaystyle\int_0^{\pi} \int_0^{4 \sin \theta} \int_0^{\sqrt{16-r^2}} f(r,\theta, z) r \, dz \space dr \space d\theta\)

    10. \(E\)est délimité par le cylindre circulaire droit\(r = \cos \theta\), le\(r\theta\) plan et la sphère\(r^2 + z^2 = 9\).

    11. \(E\)est situé dans le premier octant et est délimité par le paraboloïde circulaire\(z = 9 - 3r^2\), le cylindre\(r = \sqrt{3}\) et le plan\(r(\cos \theta + \sin \theta) = 20 - z\).

    Réponse

    un.\(E = \big\{(r,\theta,z) \, | \, 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq r \leq \sqrt{3}, \space 9 - r^2 \leq z \leq 10 - r(\cos \theta + \sin \theta)\big\}\)

    b.\(\displaystyle\int_0^{\pi/2} \int_0^{\sqrt{3}} \int_{9-r^2}^{10-r(\cos \theta + \sin \theta)} f(r,\theta,z) r \space dz \space dr \space d\theta\)

    12. \(E\)est situé dans le premier octant à l'extérieur du paraboloïde circulaire\(z = 10 - 2r^2\) et à l'intérieur du cylindre\(r = \sqrt{5}\) et est délimité également par les plans\(z = 20\) et\(\theta = \frac{\pi}{4}\).

    Dans les exercices 13 à 16, la fonction\(f\) et la région\(E\) sont données.

    a. Exprime la région\(E\) et la fonction\(f\) en coordonnées cylindriques.

    b. Convertissez l'intégrale\(\displaystyle \iiint_B f(x,y,z) \,dV\) en coordonnées cylindriques et évaluez-la.

    13. \(f(x,y,z) = x^2 + y^2\),\(E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 \leq 9, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x + 3\big\}\)

    Réponse

    un.\(E = \big\{(r,\theta,z)\, | \,0 \leq r \leq 3, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq z \leq r \space \cos \theta + 3\big\},\)
    \(f(r,\theta,z) = \frac{1}{r \space \cos \theta + 3}\)

    b.\(\displaystyle \int_0^3 \int_0^{\pi/2} \int_0^{r \space \cos \theta+3} \frac{r}{r \space \cos \theta + 3} \, dz \space d\theta \space dr = \frac{9\pi}{4}\)

    14. \(f(x,y,z) = x^2 + y^2, \space E = \big\{(x,y,z) |0 \leq x^2 + y^2 \leq 4, \space y \geq 0, \space 0 \leq z \leq 3 - x \big\}\)

    15. \(f(x,y,z) = x, \space E = \big\{(x,y,z)\, | \,1 \leq y^2 + z^2 \leq 9, \space 0 \leq x \leq 1 - y^2 - z^2\big\}\)

    Réponse

    un\(y = r \space \cos \theta, \space z = r \space \sin \theta, \space x = z,\space E = \big\{(r,\theta,z)\, | \,1 \leq r \leq 3, \space 0 \leq \theta \leq 2\pi, \space 0 \leq z \leq 1 - r^2\big\}, \space f(r,\theta,z) = z\) ;.

    b.\(\displaystyle \int_1^3 \int_0^{2\pi} \int_0^{1-r^2} z r \space dz \space d\theta \space dr = \frac{356 \pi}{3}\)

    16. \(f(x,y,z) = y, \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + z^2 \leq 9, \space 0 \leq y \leq 1 - x^2 - z^2 \big\}\)

    Dans les exercices 17 à 24, trouvez le volume du solide\(E\) dont les limites sont données en coordonnées rectangulaires.

    17. \(E\)est au-dessus du\(xy\) plan, à l'intérieur du cylindre\(x^2 + y^2 = 1\) et en dessous du plan\(z = 1\).

    Réponse
    \(\pi\)

    18. \(E\)se trouve sous le plan\(z = 1\) et à l'intérieur du paraboloïde\(z = x^2 + y^2\).

    19. \(E\)est délimité par le cône circulaire\(z = \sqrt{x^2 + y^2}\) et\(z = 1\).

    Réponse
    \(\frac{\pi}{3}\)

    20. \(E\)est situé au-dessus du\(xy\) plan, en dessous\(z = 1\), à l'extérieur de l'hyperboloïde\(x^2 + y^2 - z^2 = 1\) à une feuille et à l'intérieur du cylindre\(x^2 + y^2 = 2\).

    21. \(E\)est situé à l'intérieur du cylindre\(x^2 + y^2 = 1\) et entre les paraboloïdes circulaires\(z = 1 - x^2 - y^2\) et\(z = x^2 + y^2\).

    Réponse
    \(\pi\)

    22. \(E\)est situé à l'intérieur de la sphère\(x^2 + y^2 + z^2 = 1\), au-dessus du\(xy\) plan et à l'intérieur du cône circulaire\(z = \sqrt{x^2 + y^2}\).

    23. \(E\)est situé à l'extérieur du cône circulaire\(x^2 + y^2 = (z - 1)^2\) et entre les plans\(z = 0\) et\(z = 2\).

    Réponse
    \(\frac{4\pi}{3}\)

    24. \(E\)est situé à l'extérieur du cône circulaire\(z = 1 - \sqrt{x^2 + y^2}\), au-dessus du\(xy\) plan -, en dessous du paraboloïde circulaire et entre les plans\(z = 0\) et\(z = 2\).

    25. [T] Utilisez un système d'algèbre informatique (CAS) pour représenter graphiquement le solide dont le volume est donné par l'intégrale itérée en coordonnées cylindriques\(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^1 \int_{r^2}^r r \, dz \, dr \, d\theta.\) Trouvez le volume\(V\) du solide. Arrondissez votre réponse à quatre décimales.

    Réponse

    \(V = \frac{pi}{12} \approx 0.2618\)

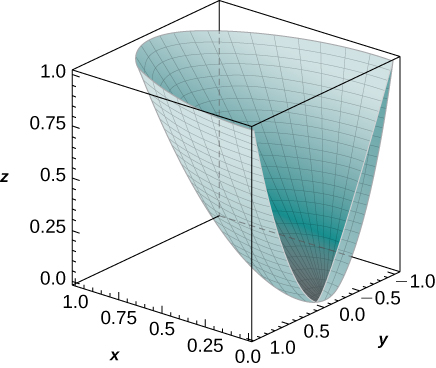
    Un quart de section d'un ellipsoïde avec une largeur 2, une hauteur de 1 et une profondeur de 1.

    26. [T] Utilisez un CAS pour représenter graphiquement le solide dont le volume est donné par l'intégrale itérée en coordonnées cylindriques\(\displaystyle \int_0^{\pi/2} \int_0^1 \int_{r^4}^r r \, dz \, dr \, d\theta.\) Find the volume \(E\) of the solid. Round your answer to four decimal places.

    27. Convert the integral \(\displaystyle\int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xz \space dz \space dx \space dy\) into an integral in cylindrical coordinates.

    Answer
    \(\displaystyle\int_0^1 \int_0^{\pi} \int_{r^2}^r zr^2 \space \cos \theta \, dz \space d\theta \space dr\)

    28. Convert the integral \(\displaystyle \int_0^2 \int_0^y \int_0^1 (xy + z) \, dz \space dx \space dy\) into an integral in cylindrical coordinates.

    In exercises 29 - 32, evaluate the triple integral \(\displaystyle \iiint_B f(x,y,z) \,dV\) over the solid \(B\).

    29. \(f(x,y,z) = 1, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 90, \space z \geq 0\big\}\)

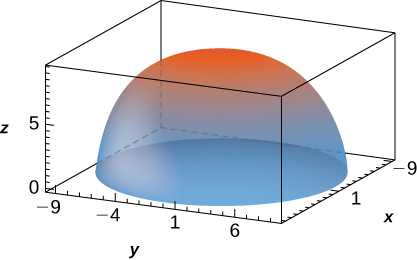
    A filled-in half-sphere with radius 3 times the square root of 10.

    [Masquer la solution]

    Réponse
    \(180 \pi \sqrt{10}\)

    30. \(f(x,y,z) = 1 - \sqrt{x^2 + y^2 + z^2}, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 9, \space y \geq 0, \space z \geq 0\big\}\)

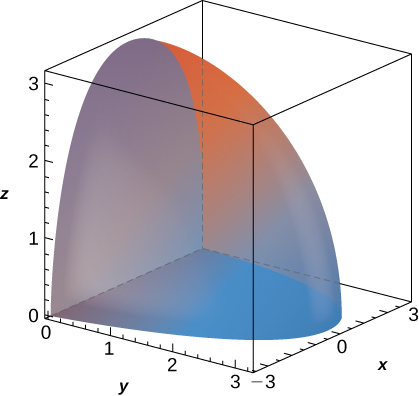
    Un quart de section d'un ovoïde d'une hauteur 8, d'une largeur de 8 et d'une longueur de 18.

    31. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B \) is bounded above by the half-sphere \(x^2 + y^2 + z^2 = 9\) with \(z \geq 0\) and below by the cone \(2z^2 = x^2 + y^2\).

    Answer
    \(\frac{81\pi(\pi - 2)}{16}\)

    32. \(f(x,y,z) = \sqrt{x^2 + y^2}, \space B \) is bounded above by the half-sphere \(x^2 + y^2 + z^2 = 16\) with \(z \geq 0\) and below by the cone \(2z^2 = x^2 + y^2\).

    33. Show that if \(F ( \rho,\theta,\varphi) = f(\rho)g(\theta)h(\varphi)\) is a continuous function on the spherical box \(B = \big\{(\rho,\theta,\varphi)\, | \,a \leq \rho \leq b, \space \alpha \leq \theta \leq \beta, \space \gamma \leq \varphi \leq \psi\big\}\), then \(\displaystyle\iiint_B F \space dV = \left(\int_a^b \rho^2 f(\rho) \space dr \right) \left( \int_{\alpha}^{\beta} g (\theta) \space d\theta \right)\left( \int_{\gamma}^{\psi} h (\varphi) \space \sin \varphi \space d\varphi \right).\)

    34. A function \(F\) is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as \(F(x,y,z) = f(\rho)\), where \(\rho = \sqrt{x^2 + y^2 + z^2}\). Show that \(\displaystyle\iiint_B F(x,y,z) \,dV = 2\pi \int_a^b \rho^2 f(\rho) \,d\rho,\) where \(B\) is the region between the upper concentric hemispheres of radii \(a\) and \(b\) centered at the origin, with \(0 < a < b\) and \(F\) a spherical function defined on \(B\).

    Use the previous result to show that \(\displaystyle\iiint_B (x^2 + y^2 + z^2) \sqrt{x^2 + y^2 + z^2} dV = 21 \pi,\) where \(B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0\big\}\).

    35. Let \(B\) be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where \(0 < a < b\). Consider F a function defined on B whose form in spherical coordinates \((\rho,\theta,\varphi)\) is \(F(x,y,z) = f(\rho)\cos \varphi\). Show that if \(g(a) = g(b) = 0\) and \(\displaystyle\int_a^b h (\rho) \, d\rho = 0,\) then \(\displaystyle\iiint_B F(x,y,z)\,dV = \frac{\pi^2}{4} [ah(a) - bh(b)],\) where \(g\) is an antiderivative of \(f\) and \(h\) is an antiderivative of \(g\).

    Use the previous result to show that \(\displaystyle \iiint_B = \frac{z \cos \sqrt{x^2 + y^2 + z^2}}{\sqrt{x^2 + y^2 + z^2}} \, dV = \frac{3\pi^2}{2},\) where \(B\) is the region between the upper concentric hemispheres of radii \(\pi\) and \(2\pi\) centered at the origin and situated in the first octant.

    In exercises 36 - 39, the function \(f\) and region \(E\) are given.

    a. Express the region \(E\) and function \(f\) in cylindrical coordinates.

    b. Convert the integral \(\displaystyle \iiint_B f(x,y,z)\, dV\) into cylindrical coordinates and evaluate it.

    36. \(f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 + z^2 \leq 1, \space z \geq 0\big\}\)

    37. \(f(x,y,z) = x + y; \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0, \space y \geq 0\big\}\)

    Answer

    a. \(f(\rho,\theta, \varphi) = \rho \space \sin \varphi \space (\cos \theta + \sin \theta), \space E = \big\{(\rho,\theta,\varphi)\, | \,1 \leq \rho \leq 2, \space 0 \leq \theta \leq \pi, \space 0 \leq \varphi \leq \frac{\pi}{2}\big\}\);

    b. \(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \int_1^2 \rho^3 \cos \varphi \space \sin \varphi \space d\rho \space d\varphi \space d\theta = \frac{15\pi}{8}\)

    38. \(f(x,y,z) = 2xy; \space E = \big\{(x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{1 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}\)

    39. \(f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 - 2x \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}\)

    Answer

    a. \(f(\rho,\theta,\varphi) = \rho \space \cos \varphi; \space E = \big\{(\rho,\theta,\varphi)\, | \,0 \leq \rho \leq 2 \space \cos \varphi, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq \varphi \leq \frac{\pi}{4}\big\}\);

    b. \(\displaystyle\int_0^{\pi/2} \int_0^{\pi/4} \int_0^{2 \space \cos \varphi} \rho^3 \sin \varphi \space \cos \varphi \space d\rho \space d\varphi \space d\theta = \frac{7\pi}{24}\)

    In exercises 40 - 41, find the volume of the solid \(E\) whose boundaries are given in rectangular coordinates.

    40. \(E = \big\{ (x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{16 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}\)

    41. \(E = \big\{ (x,y,z)\, | \,x^2 + y^2 + z^2 - 2z \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}\)

    Answer
    \(\frac{\pi}{4}\)

    42. Use spherical coordinates to find the volume of the solid situated outside the sphere \(\rho = 1\) and inside the sphere \(\rho = \cos \varphi\), with \(\varphi \in [0,\frac{\pi}{2}]\).

    43. Use spherical coordinates to find the volume of the ball \(\rho \leq 3\) that is situated between the cones \(\varphi = \frac{\pi}{4}\) and \(\varphi = \frac{\pi}{3}\).

    Answer
    \(9\pi (\sqrt{2} - 1)\)

    44. Convert the integral \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{\sqrt{16-y^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2) \, dz \, dx \, dy\) into an integral in spherical coordinates.

    45. Convert the integral \(\displaystyle \int_0^4 \int_0^{\sqrt{16-x^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^2 \, dz \space dy \space dx\) into an integral in spherical coordinates.

    Answer
    \(\displaystyle\int_0^{\pi/2} \int_0^{\pi/2} \int_0^4 \rho^6 \sin \varphi \, d\rho \, d\phi \, d\theta\)

    47. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates \(\displaystyle \int_{\pi/2}^{\pi} \int_{5\pi}^{\pi/6} \int_0^2 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.\) Find the volume \(V\) of the solid. Round your answer to three decimal places.

    Answer

    \(V = \frac{4\pi\sqrt{3}}{3} \approx 7.255\)

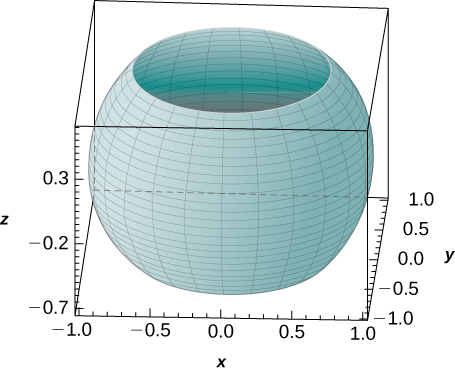
    A sphere of radius 1 with a hole drilled into it of radius 0.5.

    48. [T] Utilisez un CAS pour représenter graphiquement le solide dont le volume est donné par l'intégrale itérée en coordonnées sphériques sous la forme\(\displaystyle \int_0^{2\pi} \int_{3\pi/4}^{\pi/4} \int_0^1 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.\) Trouvez le volume\(V\) du solide. Arrondissez votre réponse à la troisième décimale.

    49. [T] Utilisez un CAS pour évaluer l'intégrale\(\displaystyle \iiint_E (x^2 + y^2) \, dV\) où\(E\) se trouve au-dessus du paraboloïde\(z = x^2 + y^2\) et au-dessous du plan\(z = 3y\).

    Réponse
    \(\frac{343\pi}{32}\)

    50. [T]

    a. Évaluez l'intégrale\(\displaystyle \iiint_E e^{\sqrt{x^2+y^2+z^2}}\, dV,\) là où elle\(E\) est délimitée par\(4x^2 + 4y^2 + 4z^2 = 1\) des sphères et\(x^2 + y^2 + z^2 = 1\).

    b. Utilisez un CAS pour trouver une approximation de l'intégrale précédente. Arrondissez votre réponse à deux décimales.

    51. Exprime le volume du solide à l'intérieur de la sphère\(x^2 + y^2 + z^2 = 16\) et à l'extérieur du cylindre\(x^2 + y^2 = 4\) sous forme d'intégrales triples en coordonnées cylindriques et en coordonnées sphériques, respectivement.

    Réponse
    \(\displaystyle \int_0^{2\pi}\int_2^4\int_{−\sqrt{16−r^2}}^{\sqrt{16−r^2}}r\,dz\,dr\,dθ\)et\(\displaystyle \int_{\pi/6}^{5\pi/6}\int_0^{2\pi}\int_{2\csc \phi}^{4}\rho^2\sin \rho \, d\rho \, d\theta \, d\phi\)

    52. Exprimez le volume du solide à l'intérieur de la sphère\(x^2 + y^2 + z^2 = 16\) et à l'extérieur du cylindre\(x^2 + y^2 = 4\) situé dans le premier octant sous forme d'intégrales triples en coordonnées cylindriques et en coordonnées sphériques, respectivement.

    53. La puissance émise par une antenne a une densité de puissance par unité de volume donnée en coordonnées sphériques par\(p(\rho,\theta,\varphi) = \frac{P_0}{\rho^2} \cos^2 \theta \space \sin^4 \varphi\), où\(P_0\) est une constante avec les unités en watts. La puissance totale dans une sphère\(B\) de\(r\) mètres de rayon est définie comme\(\displaystyle P = \iiint_B p(\rho,\theta,\varphi) \, dV.\) Trouver la puissance totale\(P\).

    Réponse
    \(P = \frac{32P_0 \pi}{3}\)watts

    54. Utilisez l'exercice précédent pour déterminer la puissance totale dans une sphère d'un rayon\(B\) de 5 mètres lorsque la densité de puissance par unité de volume est donnée par\(p(\rho, \theta,\varphi) = \frac{30}{\rho^2} \cos^2 \theta \sin^4 \varphi\).

    55. Un nuage de charge contenu dans une sphère\(B\) de rayon de\(r\) centimètres centrée à l'origine a sa densité de charge donnée par\(q(x,y,z) = k\sqrt{x^2 + y^2 + z^2}\frac{\mu C}{cm^3}\), où\(k > 0\). La charge totale contenue dans\(B\) est donnée par\(\displaystyle Q = \iiint_B q(x,y,z) \, dV.\) Trouver la charge totale\(Q\).

    Réponse
    \(Q = kr^4 \pi \mu C\)

    56. Utilisez l'exercice précédent pour trouver le nuage de charge total contenu dans la sphère unitaire si la densité de charge est de\(q(x,y,z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}\).