13.5 : Exercices de révision du chapitre 13
- Page ID
- 197233
Vrai ou faux ? Justifiez votre réponse par une preuve ou un contre-exemple.
1. Une équation paramétrique qui passe par des points\(P\) et\(Q\) peut être donnée par\(\vecs r(t)=⟨t^2,\, 3t+1,\, t−2⟩,\) où\(P(1,4,−1)\) et\(Q(16,11,2).\)
2. \(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=2\vecs u′(t)×\vecs u(t)\)
- Réponse
- Faux,\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=\vecs 0.\)
3. La courbure d'un cercle de rayon\(r\) est constante partout. De plus, la courbure est égale à\(1/r.\)
4. La vitesse d'une particule avec une fonction de position\(\vecs r(t)\) est\(\dfrac{\vecs r′(t)}{\|\vecs r′(t)\|}.\)
- Réponse
- C'est faux, c'est\(\|\vecs r′(t)\|\)
Trouvez les domaines des fonctions à valeurs vectorielles.
5. \(\vecs r(t)=⟨\sin(t),\, \ln(t),\, \sqrt{t}⟩\)
6. \(\vecs r(t)=\left\langle e^t,\,\dfrac{1}{\sqrt{4−t}},\,\sec t\right\rangle\)
- Réponse
- \(t<4, \; t≠\dfrac{nπ}{2}\)
Esquissez les courbes pour les équations vectorielles suivantes. Utilisez une calculatrice si nécessaire.
7. [T]\(\vecs r(t)=⟨t^2,\, t^3⟩\)
8. [T]\(\vecs r(t)=⟨\sin(20t)e^{−t}, \, \cos(20t)e^{−t}, \, e^{−t}⟩\)
- Réponse
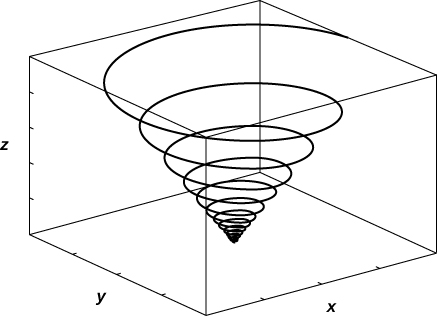
Trouvez une fonction vectorielle qui décrit les courbes suivantes.
9. Intersection du cylindre\(x^2+y^2=4\) avec le plan\(x+z=6\)
10. Intersection du cône\(z=\sqrt{x^2+y^2}\) et du plan\(z=y−4\)
- Réponse
- \(\vecs r(t)=\left\langle t, \, 2-\frac{t^2}{8},\, -2 - \frac{t^2}{8}\right\rangle\)
Trouvez les dérivées\(\vecs u(t), \, \vecs u′(t), \, \vecs u′(t)×\vecs u(t), \, \vecs u(t)×\vecs u′(t),\) et\(\vecs u(t)·\vecs u′(t).\) trouvez le vecteur tangent unitaire.
11. \(\vecs u(t)=⟨e^t, \, e^{−t}⟩\)
12. \(\vecs u(t)=⟨t^2,\, 2t+6, \, 4t^5−12⟩\)
- Réponse
- \(\vecs u′(t)=⟨2t, \, 2, \, 20t^4⟩,\)
\(\vecs u″(t)=⟨2, \, 0, \, 80t^3⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u′(t)×\vecs u(t)\Big]=⟨−480t^3−160t^4, \, 24+75t^2, \, 12+4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u′(t)\Big]=⟨480t^3+160t^4, \, -24-75t^2, \, -12-4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)⋅\vecs u′(t)\Big]=720t^8−9600t^3+6t^2+4,\)
vecteur tangent unitaire :\(\vecs T(t)=\dfrac{2t}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat i}+\dfrac{2}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat j}+\dfrac{20t^4}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat k}\)
Évaluez les intégrales suivantes.
13. \(\displaystyle ∫\left(\tan(t)\sec(t)\,\mathbf{\hat i}−te^{3t}\,\mathbf{\hat j}\right)\, dt\)
14. \(\displaystyle ∫_1^4 \vecs u(t) \, dt,\)avec\(\vecs u(t)=\left\langle\dfrac{\ln t}{t}, \, \dfrac{1}{\sqrt{t}}, \, \sin\left(\frac{tπ}{4}\right)\right\rangle\)
- Réponse
- \(\dfrac{\ln(4^2)}{2}\,\mathbf{\hat i}+2\,\mathbf{\hat j}+\dfrac{2(2+\sqrt{2})}{\pi}\,\mathbf{\hat k}\)
Trouvez la longueur des courbes suivantes.
15. \(\vecs r(t)=⟨3t,\, 4\cos t, \, 4\sin t ⟩\)pour\(1≤t≤4\)
16. \(\vecs r(t)=2\,\mathbf{\hat i}+t\,\mathbf{\hat j}+3t^2\,\mathbf{\hat k}\)pour\(0≤t≤1\)
- Réponse
- \(\dfrac{\sqrt{37}}{2}+\frac{1}{12}\sinh^{−1} 6\)
Reparamétrer les fonctions suivantes en fonction de leur longueur d'arc mesurée\(t=0\) dans le sens de l'augmentation\(t.\)
17. \(\vecs r(t)=2t\,\mathbf{\hat i}+(4t−5)\,\mathbf{\hat j}+(1−3t)\,\mathbf{\hat k}\)
18. \(\vecs r(t)=\cos(2t)\,\mathbf{\hat i}+8t\,\mathbf{\hat j}−\sin(2t)\,\mathbf{\hat k}\)
- Réponse
- \(\vecs r(t(s))=\cos\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat i}+\frac{8s}{\sqrt{65}}\,\mathbf{\hat j}−\sin\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat k}\)
Trouvez la courbure des fonctions vectorielles suivantes.
19. \(\vecs r(t)=(2\sin t)\,\mathbf{\hat i}−4t\,\mathbf{\hat j}+(2\cos t)\,\mathbf{\hat k}\)
20. \(\vecs r(t)=\sqrt{2}e^t\,\mathbf{\hat i}+\sqrt{2}e^{−t}\,\mathbf{\hat j}+2t\,\mathbf{\hat k}\)
- Réponse
- \(\dfrac{e^{2t}}{\left(e^{2t}+1\right)^2}\)
21. Trouvez le vecteur tangente unitaire, le vecteur normal unitaire et le vecteur binormal pour\(\vecs r(t)=2\cos t\,\mathbf{\hat i} +3t\,\mathbf{\hat j}+2sint\,\mathbf{\hat k}.\)
22. Trouvez les composantes d'accélération tangentielle et normale avec le vecteur de position\(\vecs r(t)=⟨\cos t,\, \sin t, \, e^t⟩.\)
- Réponse
- \(a_T=\dfrac{e^{2t}}{1+e^{2t}},\)
\(a_N=\dfrac{\sqrt{2e^{2t}+4e^{2t}\sin t\cos t+1}}{1+e^{2t}}\)
23. Un wagon à grandes roues se déplace à une vitesse constante\(v\) et a un rayon constant\(r.\) Trouvez l'accélération tangentielle et normale du wagon à grandes roues.
24. La position d'une particule est donnée par l'\(\vecs r(t)=⟨t^2, \, \ln t, \, \sin(πt)⟩,\)endroit où elle\(t\) est mesurée en secondes et\(r\) est mesurée en mètres. Trouvez les fonctions de vitesse, d'accélération et de vitesse. Quelles sont la position, la vitesse, la vitesse et l'accélération de la particule en 1 seconde ?
- Réponse
- \(\vecs v(t)=\left\langle 2t,\, \frac{1}{t}, \, \pi\cos(πt)\right\rangle\text{ m/sec},\)
\(\vecs a(t)=\left\langle 2, \, −\frac{1}{t^2}, \, −\pi^2\sin(πt) \right\rangle\text{ m/sec}^2,\)
\(\text{speed}(t)=\sqrt{4t^2+\frac{1}{t^2}+\pi^2\cos^2(πt)}\text{ m/sec}\);
À\(t=1,\; \vecs r(1)=⟨1,0,0⟩\) m,\(\vecs v(1)=⟨2,−1,\pi⟩\) m/sec,\(\vecs a(1)=⟨2,−1,0⟩\) m/sec 2 et\(\text{speed}(1) =\sqrt{5+\pi^2}\) m/sec
Les problèmes suivants concernent le lancement d'un boulet de canon à partir d'un canon. Le boulet de canon est tiré du canon avec un angle\(θ\) et une vitesse initiale.\(\vecs v_0.\) La seule force qui agit sur le boulet est la gravité, nous commençons donc par une accélération constante\(\vecs a(t)=−g\,\mathbf{\hat j}.\)
25. Trouvez la fonction vectorielle de vitesse\(\vecs v(t).\)
26. Trouvez le vecteur de position\(\vecs r(t)\) et la représentation paramétrique de la position.
- Réponse
- \(\vecs r(t)=\vecs v_0t−\dfrac{gt^2}{2}\,\mathbf{\hat j},\)
\(\vecs r(t)=⟨v_0(\cos θ)t,\,v_0(\sin θ)t,−\dfrac{gt^2}{2}⟩\)où\(v_0 = \|\vecs v_0\|.\)
27. À quel angle devez-vous tirer le boulet de canon pour que la distance horizontale soit la plus grande possible ? Quelle est la distance totale qu'il parcourrait ?


