Skip to main content
Global

13.3E : Exercices pour la section 13.3

  1. Last updated
  2. Save as PDF
  • Page ID
    197209

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Déterminer la longueur d'arc

    Dans les questions 1 à 5, trouvez la longueur de l'arc de la courbe sur l'intervalle donné.

    1)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+(2t^2+1)\,\hat{\mathbf{j}}, \quad 1≤t≤3\)

    Réponse
    \(8\sqrt{5}\)unités

    2)\(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+14t \,\hat{\mathbf{j}},\quad 0≤t≤7\). Cette partie du graphique est présentée ici :

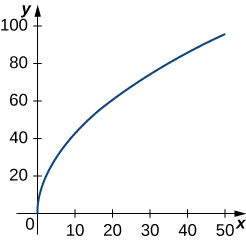
    3)\(\vecs r(t)=⟨t^2+1,4t^3+3⟩, \quad −1≤t≤0\)

    Réponse
    \(\frac{1}{54}(37^{3/2}−1)\)unités

    4)\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩,\quad 0≤t≤π\). Cette partie du graphique est présentée ici :

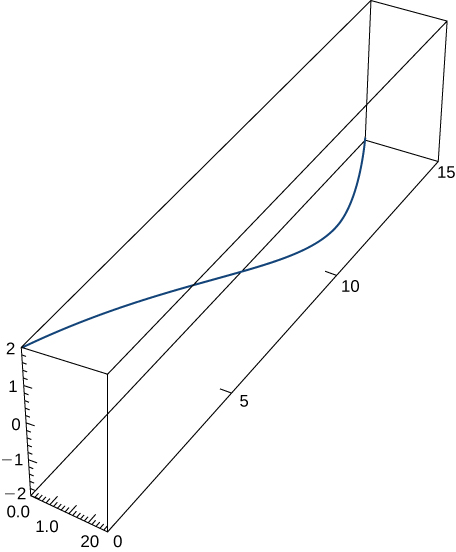
    5)\(\vecs r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩\) pendant l'intervalle\([0,\frac{π}{2}]\). Voici la partie du graphique correspondant à l'intervalle indiqué :

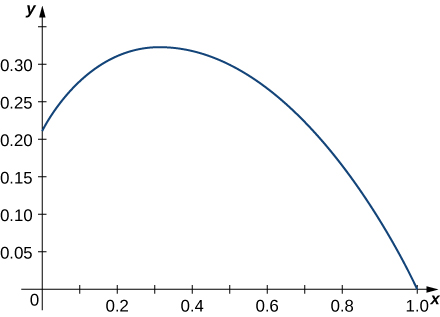
    6) Définissez une intégrale pour représenter la longueur de l'arc entre et\(t = 2\) le long de\(t = 0\) la courbe tracée par\(\vecs r(t) = \langle t, \, t^4\rangle.\) Ensuite, utilisez la technologie pour approximer cette longueur au millième d'unité le plus proche.

    7) Détermine la longueur d'un tour de l'hélice donnée par\(\vecs r(t)= \frac{1}{2} \cos t \,\hat{\mathbf{i}}+\frac{1}{2} \sin t \,\hat{\mathbf{j}}+\frac{\sqrt{3}}{2}\,t \,\hat{\mathbf{k}}\).

    Réponse
    \(=2π\)Unités de longueur

    8) Déterminez la longueur de l'arc de la fonction\(\vecs r(t)=−t \,\hat{\mathbf{i}}+4t \,\hat{\mathbf{j}}+3t \,\hat{\mathbf{k}}\) à valeur vectorielle\([0,1]\).

    9) Une particule se déplace en cercle avec l'équation du mouvement\(\vecs r(t)=3 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}} +0 \,\hat{\mathbf{k}}\). Détermine la distance parcourue par la particule autour du cercle.

    Réponse
    \(6π\)unités

    10) Définissez une intégrale pour trouver la circonférence de l'ellipse à l'aide de l'équation\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\).

    11) Détermine la longueur de la courbe\(\vecs r(t)=⟨\sqrt{2}t,\, e^t, \, e^{−t}⟩\) sur l'intervalle\(0≤t≤1\). Le graphique est présenté ici :

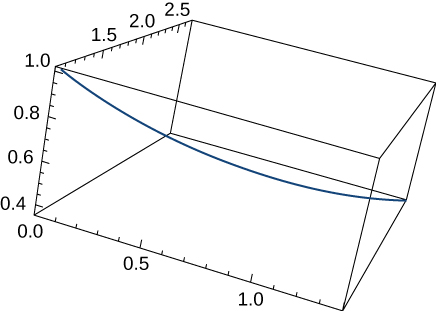
    Réponse
    \(\left(e−\frac{1}{e}\right)\)unités

    12) Trouvez la longueur de la courbe\(\vecs r(t)=⟨2 \sin t, \, 5t, \, 2 \cos t⟩\) pour\(t∈[−10,10]\).

    Vecteurs tangents unitaires et vecteurs normaux unitaires

    13) La fonction de position d'une particule est\(\vecs r(t)=a \cos( ωt) \,\hat{\mathbf{i}}+b \sin (ωt) \,\hat{\mathbf{j}}\). Trouvez le vecteur de tangente unitaire et le vecteur normal de l'unité à\(t=0\).

    Solution :
    \ (\ begin {align*} \ vecs r' (t) &= -aω \ sin (ωt) \, \ hat {\ mathbf {i}} +bω \ cos (ωt) \, \ hat {\ mathbf {j}} \ \ [5 points]
     \ | \ vecs r' (t) \ | &= \ sqrt {a^2 ω^2 \ sin^2 \ sin^2 2 (ωt) +b^2ω^2 \ cos^2 (ωt)} \ \ [5 points]
     \ vecs T (t) &= \ dfrac {\ vecs r' (t)} {\ | \ vecs r' (t) \ |} = \ dfrac {-aω \ sin (ωt) \, \ hat {\ mathbf {i}} +bω \ cos (ωt) \, \ hat {\ mathbf {j}}} {\ sqrt {a^2 ω^2 \ sin^2 (ωt) +b^2ω^2 \ cos^2 (ωt)}} \ \ [5 points]
     \ vecs T (0) &= \ dfrac {bω \, \ hat {\ mathp] bf {j}}} {\ sqrt {(bω) ^2}} = \ dfrac {bω \, \ hat {\ mathbf {j}}} {|bω|} \ end {align*} \)

    Si\(bω > 0, \; \vecs T(0) = \hat{\mathbf{j}},\) et si\( bω < 0, \; T(0)= -\hat{\mathbf{j}}\)
    Réponse
    Si\(bω > 0, \; \vecs T(0)= \hat{\mathbf{j}},\) et si\( bω < 0, \; \vecs T(0)= -\hat{\mathbf{j}}\)

    Si\(a > 0, \; \vecs N(0)= -\hat{\mathbf{i}},\) et si\( a < 0, \; \vecs N(0)= \hat{\mathbf{i}}\)

    14) Étant donné\(\vecs r(t)=a \cos (ωt) \,\hat{\mathbf{i}} +b \sin (ωt) \,\hat{\mathbf{j}}\), trouvez le vecteur binormal\(\vecs B(0)\).

    15) Étant donné\(\vecs r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩\), déterminez le vecteur tangent unitaire\(\vecs T(t)\).

    Réponse
    \ (\ begin {align*} \ vecs T (t) &= \ left \ langle \ frac {2} {\ sqrt {6}}, \, \ frac {\ cos t− \ sin t} {\ sqrt {6}}, \, \ frac {\ cos t+ \ sin t} {\ sqrt {6}} \ droite \ triangle \ \ [4pt]
    &= \ left \ langle \ frac {\ sqrt {6}} {3}, \, \ frac {\ sqrt {6}} {6} (\ cos t− \ sin t), \, \ frac {\ sqrt {6}} {6} (\ cos t+ \ sin t) \ droite \ rangle \ fin { aligner*} \)

    16) Étant donné\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), trouvez le vecteur tangent unitaire\(\vecs T(t)\) évalué à\(t=0\),\(\vecs T(0)\).

    17) Étant donné\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), déterminez le vecteur normal unitaire\(\vecs N(t)\).

    Réponse
    \(\vecs N(t)=⟨0,\, -\frac{\sqrt{2}}{2} (\sin t + \cos t), \, \frac{\sqrt{2}}{2} (\cos t- \sin t)⟩\)

    18) Étant donné\(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), trouvez le vecteur normal unitaire\(\vecs N(t)\) évalué à\(t=0\),\(\vecs N(0)\).

    Réponse
    \(\vecs N(0)=⟨0, \;-\frac{\sqrt{2}}{2},\;\frac{\sqrt{2}}{2}⟩\)

    19) Étant donné\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\), trouvez le vecteur tangent unitaire\(\vecs T(t)\). Le graphique est présenté ici :

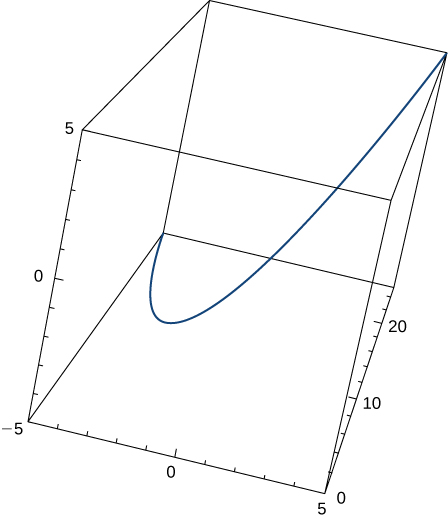
    Réponse
    \(\vecs T(t)=\dfrac{1}{\sqrt{4t^2+2}}<1,2t,1>\)

    20) Trouvez le vecteur tangente unitaire\(\vecs T(t)\) et le vecteur normal unitaire\(\vecs N(t)\) à\(t=0\) pour la courbe plane\(\vecs r(t)=⟨t^3−4t,5t^2−2⟩\). Le graphique est présenté ici :

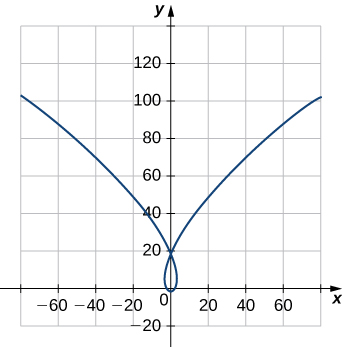
    21) Trouvez le vecteur de tangente unitaire\(\vecs T(t)\) pour\(\vecs r(t)=3t \,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}+2t \,\hat{\mathbf{k}}\).

    Réponse
    \(\vecs T(t)=\dfrac{1}{\sqrt{100t^2+13}}(3 \,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}})\)

    22) Trouvez le vecteur normal principal de la courbe\(\vecs r(t)=⟨6 \cos t,6 \sin t⟩\) au point déterminé par\(t=\frac{π}{3}\).

    23)\(\vecs T(t)\) Recherchez la courbe\(\vecs r(t)=(t^3−4t) \,\hat{\mathbf{i}}+(5t^2−2) \,\hat{\mathbf{j}}\).

    Réponse
    \(\vecs T(t)=\dfrac{1}{\sqrt{9t^4+76t^2+16}}\big((3t^2−4)\,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}\big)\)

    24)\(\vecs N(t)\) Recherchez la courbe\(\vecs r(t)=(t^3−4t)\,\hat{\mathbf{i}}+(5t^2−2)\,\hat{\mathbf{j}}\).

    25) Trouvez le vecteur de tangente unitaire\(\vecs T(t)\) pour\(\vecs r(t)=⟨2 \sin t,\, 5t,\, 2 \cos t⟩\).

    Réponse
    \(\vecs T(t)=⟨\frac{2\sqrt{29}}{29}\cos t,\, \frac{5\sqrt{29}}{29},\,−\frac{2\sqrt{29}}{29}\sin t⟩\)

    26) Trouvez le vecteur normal de l'unité\(\vecs N(t)\) pour\(\vecs r(t)=⟨2\sin t,\,5t,\,2\cos t⟩\).

    Réponse
    \(\vecs N(t)=⟨−\sin t,\, 0,\, −\cos t⟩\)

    Paramétrisations de longueur d'arc

    27) Trouvez la fonction de longueur d'arc\(\vecs s(t)\) pour le segment de ligne indiqué par\(\vecs r(t)=⟨3−3t,\, 4t⟩\). Écrivez ensuite le paramétrage de la longueur d'arc de\(r\) avec\(s\) comme paramètre.

    Réponse
    Fonction de longueur d'arc :\(s(t)=5t\) ; Paramétrage de la longueur d'arc de\(\vecs r(t)\) :\(\vecs r(s)=\left(3−\dfrac{3s}{5}\right)\,\hat{\mathbf{i}}+\dfrac{4s}{5}\,\hat{\mathbf{j}}\)

    28) Paramétrez l'hélice à l'\(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+ \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\)aide du paramètre de longueur de l'arc\(s\), à partir de\(t=0\).

    29) Paramétérisez la courbe à l'aide du paramètre de longueur de l'arc\(s\), au point où\(t=0\)\(\vecs r(t)=e^t \sin t \,\hat{\mathbf{i}} + e^t \cos t \,\hat{\mathbf{j}}\)

    Réponse
    \(\vecs r(s)=\left(1+\dfrac{s}{\sqrt{2}}\right) \sin \left( \ln \left(1+ \dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{i}} +\left(1+ \dfrac{s}{\sqrt{2}}\right) \cos \left( \ln \left(1+\dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{j}}\)

    Courbure et cercle osculant

    30) Déterminez la courbure de la courbe\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}\) à\(t=π/3\). (Remarque : le graphique est une ellipse.)

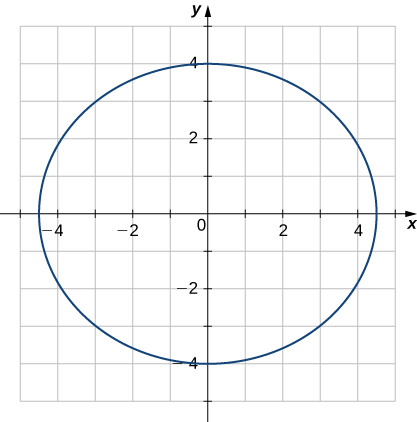
    31) Trouvez la\(x\) coordonnée pour laquelle la courbure de la courbe\(y=1/x\) est une valeur maximale.

    Réponse
    La valeur maximale de la courbure se trouve à\(x=1\).

    32) Déterminez la courbure de la courbe\(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+5 \sin t \,\hat{\mathbf{j}}\). La courbure dépend-elle du paramètre\(t\) ?

    33) Déterminez\(κ\) la courbure de la courbe\(y=x−\frac{1}{4}x^2\) au point\(x=2\).

    Réponse
    \(\frac{1}{2}\)

    34) Détermine la courbure\(κ\) de la courbe\(y=\frac{1}{3}x^3\) au point\(x=1\).

    35) Déterminez la courbure\(κ\) de la courbe\(\vecs r(t)=t \,\hat{\mathbf{i}}+6t^2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}\). Le graphique est présenté ici :

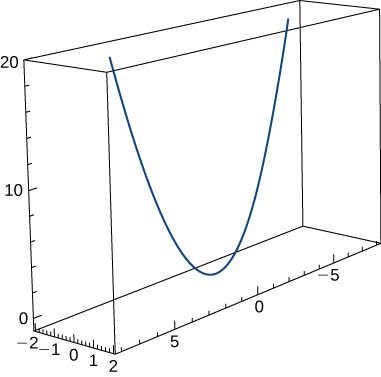
    Réponse
    \(κ≈\dfrac{49.477}{(17+144t^2)^{3/2}}\)

    36) Déterminez la courbure de\(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩\).

    37) Détermine la courbure d'\(\vecs r(t)=\sqrt{2}t \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+e^{−t} \,\hat{\mathbf{k}}\)un point\(P(0,1,1)\).

    Réponse
    \(\frac{1}{2\sqrt{2}}\)

    38) À quel point la courbure de la courbe\(y=e^x\) est-elle maximale ?

    39) Qu'advient-il de la courbure par\(x→∞\) rapport à la courbe\(y=e^x\) ?

    Réponse
    La courbure est proche de zéro.

    40) Détermine le point de courbure maximale sur la courbe\(y=\ln x\).

    41) Détermine les équations du plan normal et du plan osculant de la courbe\(\vecs r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩\) au point\((0,π,−2)\).

    Réponse
    \(y=6x+π\)et\(x+6y=6π\)

    42) Trouvez les équations des cercles osculants de l'\(4y^2+9x^2=36\)ellipse aux points\((2,0)\) et\((0,3)\).

    43) Trouvez l'équation du plan osculant au point de\(t=π/4\) la courbe\(\vecs r(t)=\cos (2t) \,\hat{\mathbf{i}}+ \sin (2t) \,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\).

    Réponse
    \(x+2z=\frac{π}{2}\)

    44) Détermine le rayon de courbure d'\(6y=x^3\)au point\((2,\frac{4}{3}).\)

    45) Déterminez la courbure en chaque point\((x,y)\) de l'hyperbole\(\vecs r(t)=⟨a \cosh( t),b \sinh (t)⟩\).

    Réponse
    \(\dfrac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}\)

    46) Calculez la courbure de l'hélice circulaire\(\vecs r(t)=r \sin (t) \,\hat{\mathbf{i}}+r \cos (t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\).

    47) Détermine le rayon de courbure\(y= \ln (x+1)\) d'un point\((2,\ln 3)\).

    Réponse
    \(\frac{10\sqrt{10}}{3}\)

    48) Détermine le rayon de courbure de l'hyperbole\(xy=1\) au point\((1,1)\).

    Une particule se déplace le long de la courbe plane\(C\) décrite par\(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}\). Utilisez ce paramétrage pour répondre aux questions 49 à 51.

    49) Détermine la longueur de la courbe sur l'intervalle\([0,2]\).

    Réponse
    \(\frac{1}{4}\big[ 4\sqrt{17} + \ln\left(4+\sqrt{17}\right)\big]\text{ units }\approx 4.64678 \text{ units}\)

    50) Détermine la courbure de la courbe plane à\(t=0,1,2\).

    51) Décrivez la courbure lorsqu'elle augmente de\(t=0\) à\(t=2\).

    Réponse
    La courbure diminue au cours de cet intervalle.

    La surface d'une grande coupelle est formée en faisant pivoter le graphe de la fonction\(y=0.25x^{1.6}\) de\(x=0\) vers\(x=5\) autour de l'\(y\)axe (mesuré en centimètres).

    52) [T] Utilisez la technologie pour représenter graphiquement la surface.

    53) Détermine la courbure\(κ\) de la courbe génératrice en fonction de\(x\).

    Réponse
    \(κ=\dfrac{30}{x^{2/5}\left(25+4x^{6/5}\right)^{3/2}}\)

    Notez qu'au départ, votre réponse peut être la suivante :
     \ (\ begin {align*} \ dfrac {6} {25x^ {2/5} \ left (1+ \ frac {4} {25} x^ {6/5} \ right) ^ {3/2}} &= \ dfrac {6} {25x^ {2/
    \(\dfrac{6}{25x^{2/5}\left(1+\frac{4}{25}x^{6/5}\right)^{3/2}}\)

    5} \ grand [\ frac {1} {25} \ gauche (25+4x^ {6/5} \ droite) \ grand] ^ {3/2}} \ \ [4 points]
    &= \ dfrac {6} {25x^ {2/5} \ gauche (\ frac {1} {25} \ droite) ^ {3/2} \ grand [25+4x^ {6/5} \ grand] ^ {3/2} \ grand] ^ {3/2}} \ \ [4 points]
    &= \ dfrac {6} {\ frac {25} {125} x^ {2/5} \ grand [25+4x^ {6/5} \ grand] ^ {3/2}} \ \ [4 points]
    &= \ dfrac {30} {x^ {2/ 5} \ left (25+4x^ {6/5} \ right) ^ {3/2}} \ end {align*} \)

    54) [T] Utilisez la technologie pour représenter graphiquement la fonction de courbure.

    Contributeurs :