13.3 : Longueur et courbure de l'arc
- Page ID
- 197201
- Déterminez la longueur du trajet d'une particule dans l'espace à l'aide de la fonction de longueur d'arc.
- Expliquez la signification de la courbure d'une courbe dans l'espace et énoncez sa formule.
- Décrivez la signification des vecteurs normal et binormal d'une courbe dans l'espace.
Dans cette section, nous étudions les formules relatives aux courbes en deux et en trois dimensions et voyons comment elles sont liées aux différentes propriétés d'une même courbe. Supposons, par exemple, qu'une fonction à valeur vectorielle décrit le mouvement d'une particule dans l'espace. Nous aimerions déterminer la distance parcourue par la particule sur un intervalle de temps donné, qui peut être décrit par la longueur de l'arc de la trajectoire qu'elle suit. Ou supposons que la fonction à valeur vectorielle décrit une route que nous construisons et que nous souhaitions déterminer la netteté de la courbe de la route en un point donné. Ceci est décrit par la courbure de la fonction à ce point. Nous explorons chacun de ces concepts dans cette section.
Longueur d'arc pour les fonctions vectorielles
Nous avons vu comment une fonction à valeur vectorielle décrit une courbe en deux ou trois dimensions. Rappelons que la formule de la longueur d'arc d'une courbe définie par les fonctions paramétriques\(x=x(t),y=y(t),t_1≤t≤t_2\) est donnée par
\[s=\int^{t_2}_{t_1} \sqrt{(x′(t))^2+(y′(t))^2}dt. \nonumber \]
De la même manière, si nous définissons une courbe lisse à l'aide d'une fonction à valeur vectorielle\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}\)\(a≤t≤b\), où la longueur de l'arc est donnée par la formule
\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2}dt. \nonumber \]
En trois dimensions, si la fonction à valeur vectorielle est décrite par\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}\) sur le même intervalle\(a≤t≤b\), la longueur de l'arc est donnée par
\[s=\int^{b}_{a} \sqrt{(f′(t))^2+(g′(t))^2+(h′(t))^2}dt. \nonumber \]
Courbe plane : étant donné une courbe lisse\(C\) définie par la fonction\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \, \hat{\mathbf{j}}\), où\(t\) se trouve dans l'intervalle\([a,b]\), la longueur de l'arc\(C\) sur l'intervalle est
\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc2D}\end{align} \]
Courbe spatiale : étant donné une courbe lisse\(C\) définie par la fonction\(\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}}\), où\(t\) se trouve dans l'intervalle\([a,b]\), la longueur de l'arc\(C\) sur l'intervalle est
\[\begin{align} s &=\int^{b}_{a} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2}dt \\[4pt] &=\int^{b}_{a} \|\vecs r′(t)\|dt . \label{Arc3D} \end{align} \]
Les deux formules sont très similaires ; elles ne diffèrent que par le fait qu'une courbe spatiale possède trois fonctions composantes au lieu de deux. Notez que les formules sont définies pour les courbes lisses, c'est-à-dire les courbes où la fonction à valeur vectorielle\(\vecs r(t)\) est dérivable par une dérivée non nulle. La condition de lissage garantit que la courbe ne présente aucune pointe (ou angle) susceptible de rendre la formule problématique.
Calculez la longueur de l'arc pour chacune des fonctions à valeurs vectorielles suivantes :
- \(\vecs r(t)=(3t−2) \,\hat{\mathbf{i}}+(4t+5) \,\hat{\mathbf{j}},\quad 1≤t≤5\)
- \(\vecs r(t)=⟨t\cos t,t\sin t,2t⟩,0≤t≤2 \pi \)
Solution
- En utilisant l'équation \ ref {Arc2D}\(\vecs r′(t)=3 \,\hat{\mathbf{i}}+4 \,\hat{\mathbf{j}}\), donc
\[\begin{align*} s &=\int^{b}_{a} \|\vecs r′(t)\|dt \\[4pt] &=\int^{5}_{1} \sqrt{3^2 + 4^2} dt \\[4pt] &=\int^{5}_{1} 5 dt = 5t\big|^{5}_{1} = 20. \end{align*}\]
- En utilisant l'équation \ ref {Arc3D}\(\vecs r′(t)=⟨ \cos t−t \sin t, \sin t+t \cos t,2⟩ \), donc
\[\begin{align*} s &=\int^{b}_{a} ∥\vecs r′(t)∥dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{(\cos t−t \sin t)^2+( \sin t+t \cos t)^2+2^2} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{( \cos ^2 t−2t \sin t \cos t+t^2 \sin ^2 t)+( \sin^2 t+2t \sin t \cos t+t^2 \cos ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{\cos ^2 t+ \sin^2 t+t^2( \cos ^2 t+ \sin ^2 t)+4} dt \\[4pt] &=\int^{2 \pi}_{0} \sqrt{t^2+5} dt\end{align*}\]
Ici, nous pouvons utiliser une formule d'intégration tabulaire
\[\int \sqrt{u^2+a^2}du = \dfrac{u}{2}\sqrt{u^2+a^2} + \dfrac{a^2}{2} \ln \,\left|\, u + \sqrt{u^2+a^2} \,\right| + C, \nonumber \]
nous obtenons donc
\[\begin{align*} \int^{2 \pi}_{0} \sqrt{t^2+5} dt \; &= \frac{1}{2} \bigg( t \sqrt{t^2+5}+5 \ln \,\left|t+\sqrt{t^2+5}\right| \bigg) _0^{2π} \\[4pt] &= \frac{1}{2} \bigg( 2π \sqrt{4π^2+5}+5 \ln \bigg( 2π+ \sqrt{4π^2+5} \bigg) \bigg)−\frac{5}{2} \ln \sqrt{5} \\[4pt] &≈25.343 \,\text{units}. \end{align*}\]
Calculez la longueur de l'arc de la courbe paramétrée
\[\vecs r(t)=⟨2t^2+1,2t^2−1,t^3⟩,\quad 0≤t≤3. \nonumber \]
- Allusion
-
Utilisez l'équation \ ref {Arc3D}.
- Réponse
-
\(\vecs r′(t)=⟨4t,4t,3t^2⟩,\)donc\(s= \frac{1}{27}(113^{3/2}−32^{3/2})≈37.785\) unités
Nous revenons maintenant à l'hélice présentée plus tôt dans ce chapitre. Une fonction à valeur vectorielle qui décrit une hélice peut être écrite sous la forme
\[\vecs r(t)=R \cos \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}} +R \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}},0≤t≤h, \nonumber \]
où\(R\) représente le rayon de l'hélice,\(h\) représente la hauteur (distance entre deux tours consécutifs) et l'hélice complète les\(N\) tours. Dérivons une formule pour la longueur de l'arc de cette hélice à l'aide de l'équation \ ref {Arc3D}. Tout d'abord,
\[\vecs r′(t)=−\dfrac{2πNR}{h} \sin \left(\dfrac{2πNt}{h}\right) \,\hat{\mathbf{i}}+ \dfrac{2πNR}{h} \cos \left(\dfrac{2πNt}{h} \right) \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}. \nonumber \]
Par conséquent,
\[\begin{align*} s & =\int_a^b ‖\vecs r′(t)‖dt \\[4pt] &=\int_0^h\sqrt{ \bigg(−\dfrac{2πNR}{h} \sin \bigg(\dfrac{2πNt}{h} \bigg) \bigg)^2+ \bigg( \dfrac{2πNR}{h} \cos \bigg( \dfrac{2πNt}{h} \bigg) \bigg)^2+1^2}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} \bigg( \sin ^2 \bigg(\dfrac{2πNt}{h} \bigg) + \cos ^2 \bigg( \dfrac{2πNt}{h} \bigg) \bigg)+1}dt \\[4pt] &=\int_0^h\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}dt \\[4pt] &=\bigg[ t\sqrt{ \dfrac{4π^2N^2R^2}{h^2} +1}\bigg]^h_0 \\[4pt] &=h \sqrt{ \dfrac{4π^2N^2R^2 + h^2}{h^2}} \\[4pt] &=\sqrt{ 4π^2N^2R^2 + h^2}.\end{align*}\]
Cela donne une formule pour la longueur d'un fil nécessaire pour former une hélice dont les\(N\) spires ont un rayon\(R\) et une hauteur\(h\).
Paramétrage de la longueur d'arc
Nous avons maintenant une formule pour la longueur d'arc d'une courbe définie par une fonction à valeur vectorielle. Allons encore plus loin et examinons ce qu'est une fonction de longueur d'arc.
Si une fonction à valeur vectorielle représente la position d'une particule dans l'espace en fonction du temps, la fonction de longueur d'arc mesure la distance parcourue par cette particule en fonction du temps. La formule de la fonction de longueur d'arc découle directement de la formule de la longueur de l'arc :
\[s=\int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du. \label{arclength2} \]
Si la courbe est en deux dimensions, seuls deux termes apparaissent sous la racine carrée à l'intérieur de l'intégrale. La raison de l'utilisation de la variable indépendante u est de faire la distinction entre le temps et la variable d'intégration. Puisque\(s(t)\) mesure la distance parcourue en fonction du temps,\(s′(t)\) mesure la vitesse de la particule à un moment donné. Puisque nous avons une formule pour\(s(t)\) dans l'équation \ ref {arclength2}, nous pouvons différencier les deux côtés de l'équation :
\[ \begin{align*} s′(t) &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} \sqrt{(f′(u))^2+(g′(u))^2+(h′(u))^2}du \bigg] \\[4pt] &=\dfrac{d}{dt} \bigg[ \int^{t}_{a} ‖\vecs r′(u)‖du \bigg] \\[4pt] &=\|\vecs r′(t)\|.\end{align*}\]
Si nous supposons que cela\(\vecs r(t)\) définit une courbe lisse, alors la longueur de l'arc augmente toujours, donc\(s′(t)>0\) de\(t>a\). Enfin, si\(\vecs r(t)\) c'est une courbe sur laquelle,\(\|\vecs r′(t)\|=1 \) pour tous\(t\),
\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du=\int^{t}_{a} 1\,du=t−a, \nonumber \]
ce qui signifie que cela\(t\) représente la longueur de l'arc aussi longue que\(a=0\).
\(\vecs r(t)\)Décrivons une courbe lisse pour\(t≥a\). Ensuite, la fonction de longueur d'arc est donnée par
\[s(t)=\int^{t}_{a} ‖\vecs r′(u)‖\,du \nonumber \]
En outre,
\[\dfrac{ds}{dt}=‖\vecs r′(t)‖>0. \nonumber \]
Si\(‖\vecs r′(t)‖=1\) ce paramètre est égal à tous\(t≥a\), alors le paramètre\(t\) représente la longueur de l'arc à partir du point de départ à\(t=a\).
Une application utile de ce théorème consiste à trouver un paramétrage alternatif d'une courbe donnée, appelé paramétrage de la longueur de l'arc. Rappelons que toute fonction à valeur vectorielle peut être reparamétrée via un changement de variables. Par exemple, si nous avons une fonction\(\vecs r(t)=⟨3 \cos t,3 \sin t⟩,0≤t≤2π\) qui paramètre un cercle de rayon 3, nous pouvons modifier le paramètre de\(t\) à\(4t\), pour obtenir un nouveau paramétrage\(\vecs r(t)=⟨3 \cos 4t,3 \sin 4t⟩\). Le nouveau paramétrage définit toujours un cercle de rayon 3, mais il ne nous reste plus qu'à utiliser les valeurs\(0≤t≤π/2\) pour traverser le cercle une seule fois.
Supposons que nous trouvions la fonction de longueur d'arc\(s(t)\) et que nous soyons capables de résoudre cette fonction\(t\) en fonction de\(s\). Nous pouvons ensuite reparamétrer la fonction d'origine\(\vecs r(t)\) en remplaçant l'expression par\(t\) back into\(\vecs r(t)\). La fonction à valeur vectorielle est désormais écrite en termes de paramètre\(s\). Puisque la variable\(s\) représente la longueur de l'arc, nous appelons cela un paramétrage de la longueur d'arc de la fonction d'origine\(\vecs r(t)\). L'un des avantages de trouver le paramétrage de la longueur de l'arc est que la distance parcourue le long de la courbe à partir de celle-ci\(s=0\) est désormais égale au paramètre\(s\). Le paramétrage de la longueur de l'arc apparaît également dans le contexte de la courbure (que nous examinerons plus loin dans cette section) et des intégrales de lignes.
Trouvez le paramétrage de la longueur de l'arc pour chacune des courbes suivantes :
- \(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+ 4 \sin t \,\hat{\mathbf{j}},\quad t≥0\)
- \(\vecs r(t)=⟨t+3,2t−4,2t⟩,\quad t≥3\)
Solution
- Nous trouvons d'abord la fonction de longueur d'arc en utilisant l'équation \ ref {arclength2} :
\[\begin{align*} s(t) &= \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_0^t ‖⟨−4 \sin u,4 \cos u⟩‖ \,du \\[4pt] &= \int_0^t \sqrt{(−4 \sin u)^2+(4 \cos u)^2} \,du \\[4pt] &= \int_0^t \sqrt{16 \sin ^2 u+16 \cos ^2 u} \,du \\[4pt] &= \int_0^t 4\,du = 4t, \end{align*}\]
- qui donne la relation entre la longueur de l'arc\(s\) et le paramètre\(t\)\(s=4t;\) ainsi,\(t=s/4\). Ensuite, nous remplaçons la variable\(t\) dans la fonction\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}\) d'origine par l'expression\(s/4\) pour obtenir
\[\vecs r(s)=4 \cos \left(\frac{s}{4}\right) \,\hat{\mathbf{i}} + 4 \sin \left( \frac{s}{4}\right) \,\hat{\mathbf{j}}. \nonumber \]
Il s'agit du paramétrage de la longueur d'arc de\(\vecs r(t)\). Puisque la restriction initiale sur\(t\) a été donnée par\(t≥0\), la restriction sur s devient\(s/4≥0\), ou\(s≥0\). - La fonction de longueur d'arc est donnée par l'équation \ ref {arclength2} :
\[\begin{align*} s(t) & = \int_a^t ‖\vecs r′(u)‖ \,du \\[4pt] &= \int_3^t ‖⟨1,2,2⟩‖ \,du \\[4pt] &= \int_3^t \sqrt{1^2+2^2+2^2} \,du \\[4pt] &= \int_3^t 3 \,du \\[4pt] &= 3t - 9. \end{align*}\]
Par conséquent, la relation entre la longueur de l'arc\(s\) et le paramètre\(t\) est\(s=3t−9\) vraie\(t= \frac{s}{3}+3\). En la remplaçant par la fonction d'origine, vous\(\vecs r(t)=⟨t+3,2t−4,2t⟩ \) obtenez\[\vecs r(s)=⟨\left(\frac{s}{3}+3\right)+3,\,2\left(\frac{s}{3}+3\right)−4,\,2\left(\frac{s}{3}+3\right)⟩=⟨\frac{s}{3}+6, \frac{2s}{3}+2,\frac{2s}{3}+6⟩.\nonumber \]
Il s'agit d'un paramétrage de la longueur d'arc de\(\vecs r(t)\). La restriction initiale sur le paramètre\(t\) était\(t≥3\), donc la restriction sur\(s\) is\((s/3)+3≥3\), ou\(s≥0\).
Trouvez la fonction de longueur d'arc pour l'hélice
\[\vecs r(t)=⟨3 \cos t, 3 \sin t,4t⟩,\quad t≥0. \nonumber \]
Ensuite, utilisez la relation entre la longueur de l'arc et le paramètre\(t\) pour trouver un paramétrage de la longueur de l'arc de\(\vecs r(t)\).
- Allusion
-
Commencez par trouver la fonction de longueur d'arc.
- Réponse
-
\(s=5t\), ou\(t=s/5\). Le substituer à cela\(\vecs r(t)=⟨3 \cos t,3 \sin t,4t⟩\) donne
\[\vecs r(s)=⟨3 \cos \left(\frac{s}{5}\right),3 \sin \left(\frac{s}{5}\right),\frac{4s}{5}⟩,\quad s≥0 \nonumber \]
courbure
La courbure est un sujet important lié à la longueur de l'arc. Le concept de courbure permet de mesurer la vitesse de rotation d'une courbe lisse. Un cercle possède une courbure constante. Plus le rayon du cercle est petit, plus la courbure est grande.
Pensez à conduire sur une route. Supposons que la route se trouve sur un arc de grand cercle. Dans ce cas, vous n'aurez guère à tourner le volant pour rester sur la route. Supposons maintenant que le rayon soit plus petit. Dans ce cas, vous devrez tourner plus brusquement pour rester sur la route. Dans le cas d'une courbe autre qu'un cercle, il est souvent utile d'inscrire d'abord un cercle sur la courbe en un point donné afin qu'il soit tangent à la courbe en ce point et « épouse » la courbe le plus étroitement possible au voisinage du point (Figure\(\PageIndex{1}\)). La courbure du graphe à ce point est alors définie comme étant identique à la courbure du cercle inscrit.
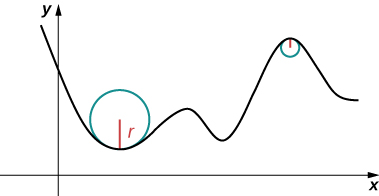
Définition : Courbure
\(C\)Soit une courbe lisse dans le plan ou dans l'espace indiqué par\(\vecs r(s)\), où\(s\) est le paramètre de longueur de l'arc. La courbure\(κ\) à\(s\) est
\[κ =\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}=‖\vecs T′(s)‖. \nonumber \]
Visionnez cette vidéo pour plus d'informations sur la courbure d'une courbe spatiale.
La formule utilisée pour définir la courbure n'est pas très utile en termes de calcul. En particulier, rappelons que\(\vecs T(t)\) représente le vecteur tangent unitaire à une fonction à valeur vectorielle donnée\(\vecs r(t)\), et que la formule pour\(\vecs T(t)\) est
\[\vecs T(t)=\frac{\vecs r′(t)}{∥\vecs r′(t)∥}. \nonumber \]
Pour utiliser la formule de la courbure, il faut d'abord l'exprimer\(\vecs r(t)\) en termes de paramètre de longueur d'arc\(s\), puis trouver le vecteur de tangente unitaire\(\vecs T(s)\) pour la fonction\(\vecs r(s)\), puis prendre la\(\vecs T(s)\) dérivée de par rapport à\(s\). Il s'agit d'un processus fastidieux. Heureusement, il existe des formules équivalentes pour la courbure.
Si\(C\) est une courbe lisse donnée par\(\vecs r(t)\), alors la courbure\(κ\) de\(C\) at\(t\) est donnée par
\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}. \label{EqK2} \]
S'il s'\(C\)agit d'une courbe tridimensionnelle, la courbure peut être donnée par la formule
\[κ =\dfrac{‖\vecs r′(t)×\vecs r′′(t)‖}{‖\vecs r′(t)‖^3}.\label{EqK3} \]
Si\(C\) est le graphe d'une fonction\(y=f(x)\)\(y′\) et que les deux\(y''\) existent, alors la courbure\(κ\) au point\((x,y)\) est donnée par
\[κ =\dfrac{|y''|}{[1+(y′)^2]^{3/2}}.\label{EqK4} \]
La première formule découle directement de la règle de la chaîne :
\[\dfrac{d\vecs{T}}{dt} = \dfrac{d\vecs{T}}{ds} \dfrac{ds}{dt}, \nonumber \]
où\(s\) est la longueur de l'arc le long de la courbe\(C\). En divisant les deux côtés par\(ds/dt\) et en prenant l'ampleur des deux côtés, on obtient
\[\bigg{\|}\dfrac{d\vecs{T}}{ds}\bigg{\|}= \left\lVert\frac{\vecs T′(t)}{\dfrac{ds}{dt}}\right\rVert.\nonumber \]
Puisque\(ds/dt=‖\vecs r′(t)‖\), cela donne la formule de la courbure\(κ\) d'une courbe\(C\) en termes de paramétrage quelconque de\(C\) :
\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}.\nonumber \]
Dans le cas d'une courbe tridimensionnelle, nous commençons par les formules\(\vecs T(t)=(\vecs r′(t))/‖\vecs r′(t)‖\) et\(ds/dt=‖\vecs r′(t)‖\). Par conséquent,\(\vecs r′(t)=(ds/dt)\vecs T(t)\). Nous pouvons prendre la dérivée de cette fonction en utilisant la formule du produit scalaire :
\[\vecs r″(t)=\dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t).\nonumber \]
En utilisant ces deux dernières équations, nous obtenons
\[\begin{align*} \vecs r′(t)×\vecs r″(t) &=\dfrac{ds}{dt}\vecs T(t)× \bigg( \dfrac{d^2s}{dt^2}\vecs T(t)+\dfrac{ds}{dt}\vecs T′(t) \bigg) \\[4pt] &=\dfrac{ds}{dt} \dfrac{d^2s}{dt^2}\vecs T(t)×\vecs T(t)+(\dfrac{ds}{dt})^2\vecs T(t)×\vecs T′(t). \end{align*}\]
Puisque\(\vecs T(t)×\vecs T(t)=0\), cela se réduit à
\[\vecs r′(t)×\vecs r′′(t)=\left(\dfrac{ds}{dt}\right)^2\vecs T(t)×\vecs T′(t).\nonumber \]
Comme\(\vecs T′\) il est parallèle à\(\vecs N\) et\(\vecs T\) orthogonal à\(\vecs N\), il s'ensuit que\(\vecs T\) et\(\vecs T′\) sont orthogonaux. Cela signifie que\(‖\vecs T×\vecs T′‖=‖\vecs T‖‖\vecs T′‖ \sin (π/2)=‖\vecs T′‖\), donc
\[\|\vecs r′(t)×\vecs r″(t)\|=\left(\dfrac{ds}{dt}\right)^2‖\vecs T′(t)‖.\nonumber \]
Maintenant, nous résolvons cette équation\(‖\vecs T′(t)‖\) et utilisons le fait que\(ds/dt=‖\vecs r′(t)‖\) :
\[‖\vecs T′(t)‖=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^2}.\nonumber \]
Ensuite, nous divisons les deux côtés par\(‖\vecs r′(t)‖\). Cela donne
\[κ =\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖}=\dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}.\nonumber \]
Cela prouve\(\ref{EqK3}\). Pour le prouver\(\ref{EqK4}\), nous partons de l'hypothèse que la courbe\(C\) est définie par la fonction\(y=f(x)\). Ensuite, nous pouvons définir\(\vecs r(t)=x \,\hat{\mathbf{i}}+f(x) \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}\). En utilisant la formule précédente pour la courbure :
\[\begin{align*} \vecs r′(t) &=\,\hat{\mathbf{i}}+f′(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r″(t) &=f″(x)\,\hat{\mathbf{j}} \\[4pt] \vecs r′(t)×\vecs r″(t) &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\ 1 & f′(x) & 0 \\ 0 & f″(x) & 0 \end{vmatrix} =f″(x)\,\hat{\mathbf{k}}. \end{align*}\]
Par conséquent,
\[κ= \dfrac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3}=\dfrac{|f″(x)|}{(1+[f′(x)]^2)^{3/2}} \nonumber \]
Détermine la courbure de chacune des courbes suivantes au point donné :
- \(\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}+4 \sin t\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}},\quad t=\dfrac{4π}{3}\)
- \(\mathrm{f(x)= \sqrt{4x−x^2},x=2}\)
Solution
- Cette fonction décrit une hélice.
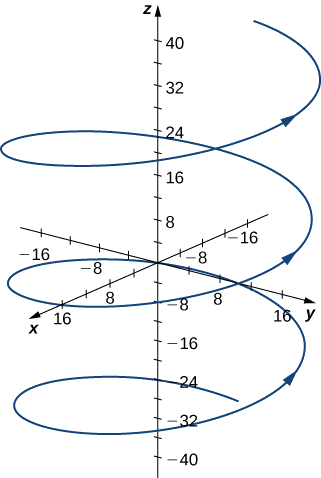
La courbure de l'hélice à\(t=(4π)/3\) peut être déterminée en utilisant\(\ref{EqK2}\). D'abord, calculez\(\vecs T(t)\) :
\[\begin{align*} \vecs T(t) &=\dfrac{\vecs r′(t)}{‖\vecs r′(t)‖} \\[4pt] &=\dfrac{⟨−4 \sin t,4 \cos t,3⟩}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+3^2}}\\[4pt] &=⟨−\dfrac{4}{5} \sin t,\dfrac{4}{5} \cos t, \dfrac{3}{5}⟩. \end{align*}\]
Ensuite, calculez\(\vecs T′(t):\)
\[\vecs T′(t)=⟨−\dfrac{4}{5} \cos t,− \dfrac{4}{5} \sin t,0⟩. \nonumber \]
Enfin, appliquez\(\ref{EqK2}\) :
\[ \begin{align*} κ &=\dfrac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} = \dfrac{‖⟨−\dfrac{4}{5} \cos t,−\dfrac{4}{5} \sin t,0⟩‖}{‖⟨−4 \sin t,4 \cos t,3⟩‖} \\[4pt] &=\dfrac{\sqrt{(−\dfrac{4}{5} \cos t)^2+(−\dfrac{4}{5} \sin t)^2+0^2}}{\sqrt{(−4 \sin t)^2+(4 \cos t)^2+ 3^2}} \\[4pt] &=\dfrac{4/5}{5}=\dfrac{4}{25}. \end{align*}\]
La courbure de cette hélice est constante en tout point de l'hélice.
- Cette fonction décrit un demi-cercle.
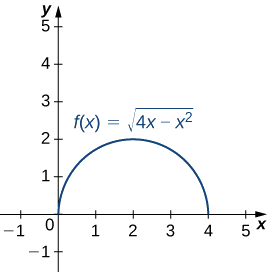
Pour trouver la courbure de ce graphe, il faut utiliser\(\ref{EqK4}\). Tout d'abord, nous calculons\(y′\) et\(y″:\)
\[\begin{align*}y &=\sqrt{4x−x^2}=(4x−x^2)^{1/2} \\[4pt] y′ &=\dfrac{1}{2}(4x−x^2)^{−1/2}(4−2x)=(2−x)(4x−x^2)^{−1/2} \\[4pt] y″ &=−(4x−x^2)^{−1/2}+(2−x)(−\dfrac{1}{2})(4x−x^2)^{−3/2}(4−2x) \\[4pt] & =−\dfrac{4x−x^2}{(4x−x^2)^{3/2}}− \dfrac{(2−x)^2}{(4x−x^2)^{3/2}} \\[4pt] &=\dfrac{x^2−4x−(4−4x+x^2)}{(4x−x^2)^{3/2}} \\[4pt] &=−\dfrac{4}{(4x−x^2)^{3/2}}. \end{align*} \nonumber \]
Ensuite, nous appliquons\(\ref{EqK4}\) :
\[ \begin{align*} κ &=\dfrac{|y''|}{[1+(y′)^2]^{3/2}} \\[4pt] &= \dfrac{\bigg| −\dfrac{4}{(4x−x^2)^{3/2}}\bigg|}{\bigg[1+((2−x)(4x−x^2)^{−1/2})^2 \bigg]^{3/2}} = \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{\bigg[ 1+\dfrac{(2−x)^2}{4x−x^2} \bigg]^ {3/2}} \\[4pt] &= \dfrac{\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg|}{ \bigg[ \dfrac{4x−x^2+x^2−4x+4}{4x−x^2} \bigg]^{3/2}}=\bigg| \dfrac{4}{(4x−x^2)^{3/2}} \bigg| ⋅\dfrac{(4x−x^2)^{3/2}}{8} \\[4pt] &=\dfrac{1}{2}. \end{align*}\]
La courbure de ce cercle est égale à l'inverse de son rayon. Il y a un problème mineur avec la valeur absolue de\(\ref{EqK4}\) ; cependant, un examen plus approfondi du calcul révèle que le dénominateur est positif pour toute valeur de\(x\).
Trouve la courbure de la courbe définie par la fonction
\[y=3x^2−2x+4 \nonumber \]
au point\(x=2\).
- Allusion
-
Utiliser\(\ref{EqK4}\).
- Réponse
-
\(κ \; =\frac{6}{101^{3/2}}≈0.0059\)
Les vecteurs normal et binormal
Nous avons vu que la dérivée\(\vecs r′(t)\) d'une fonction à valeur vectorielle est un vecteur tangent à la courbe définie par\(\vecs r(t)\), et que le vecteur tangent unitaire\(\vecs T(t)\) peut être calculé en divisant\(\vecs r′(t)\) par sa magnitude. Lors de l'étude du mouvement en trois dimensions, deux autres vecteurs sont utiles pour décrire le mouvement d'une particule le long d'une trajectoire dans l'espace : le vecteur normal unitaire principal et le vecteur binormal.
Définition : Vecteurs binoraux
\(C\)Soit une courbe lisse tridimensionnelle représentée par un\(\vecs r\) intervalle ouvert\(I\). Si\(\vecs T′(t)≠\vecs 0\), alors le vecteur normal de l'unité principale at\(t\) est défini comme étant
\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \label{EqNormal} \]
Le vecteur binormal at\(t\) est défini comme
\[\vecs B(t)=\vecs T(t)×\vecs N(t),\label{EqBinormal} \]
où\(\vecs T(t)\) est le vecteur de tangente unitaire.
Notez que, par définition, le vecteur binormal est orthogonal à la fois au vecteur tangent unitaire et au vecteur normal. De plus,\(\vecs B(t)\) c'est toujours un vecteur unitaire. Cela peut être démontré à l'aide de la formule de l'amplitude d'un produit croisé.
\[‖\vecs B(t)‖=‖\vecs T(t)×\vecs N(t)‖=‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta, \nonumber \]
où\(\theta\) est l'angle entre\(\vecs T(t)\) et\(\vecs N(t)\). Puisque\(\vecs N(t)\) c'est la dérivée d'un vecteur unitaire, la propriété (vii) de la dérivée d'une fonction à valeur vectorielle nous le dit\(\vecs T(t)\) et\(\vecs N(t)\) sont orthogonales l'une à l'autre, donc\(\theta=π/2\). De plus, ils sont tous deux des vecteurs unitaires, leur magnitude est donc de 1. Par conséquent,\(‖\vecs T(t)‖‖\vecs N(t)‖ \sin \theta=(1)(1) \sin (π/2)=1\) et\(\vecs B(t)\) est un vecteur unitaire.
Le vecteur normal unitaire principal peut être difficile à calculer car le vecteur tangent unitaire implique un quotient, et ce quotient a souvent une racine carrée dans le dénominateur. Dans le cas tridimensionnel, il peut être encore plus difficile de trouver le produit croisé du vecteur tangent unitaire et du vecteur normal unitaire. Heureusement, nous avons des formules alternatives pour trouver ces deux vecteurs, et elles sont présentées dans Motion in Space.
Pour chacune des fonctions à valeur vectorielle suivantes, trouvez le vecteur normal de l'unité principale. Ensuite, si possible, trouvez le vecteur binormal.
- \(\vecs r(t)=4 \cos t\,\hat{\mathbf{i}}− 4 \sin t\,\hat{\mathbf{j}}\)
- \(\vecs r(t)=(6t+2)\,\hat{\mathbf{i}}+5t^2\,\hat{\mathbf{j}}−8t\,\hat{\mathbf{k}}\)
Solution
- Cette fonction décrit un cercle.
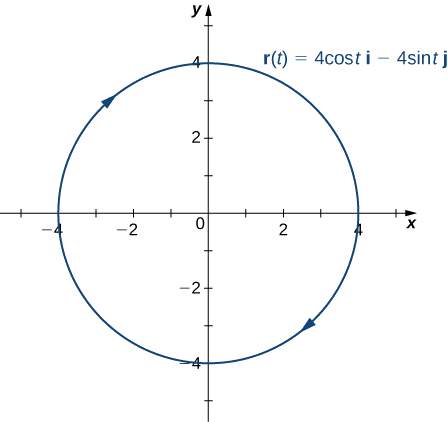
Pour trouver le vecteur normal de l'unité principale, il faut d'abord trouver le vecteur de tangente unitaire\(\vecs T(t):\)
\ [\ begin {align*} \ vecs T (t) &= \ dfrac {\ vecs r′ (t)} {] \ vecs r′ (t)} \ \ [4pt]
&= \ dfrac {−4 \ sin t \, \ hat {\ mathbf {i}} −4 \ cos t \, \ hat {\ mathbf {j}} {\ mathbf {j}} {\ mathbf {i}} −4 \ cos t \, \ hat {\ mathbf {j}} {\ mathbf {j}} sqrt {(−4 \ sin t) ^2+ (−4 \ cos t) ^2}} \ \ [4 points]
&= \ dfrac {−4 \ sin t \, \ hat {\ mathbf {i}} −4 \ cos t \, \ hat {\ mathbf {j}}} {\ sqrt {16 \ sin ^2 t+16 \ cos ^2 t}} \ \ [4 points]
&= \ dfrac {−4 \ sin t \, \ hat {\ mathbf {i}} −4 \ cos t \, \ hat {\ mathbf {j}}} {\ sqrt {16 (\ sin ^2 t+ \ cos ^2 t)}} \ \ [4 points]
&= \ dfrac {−4 \ sin t \, \ hat {\ mathbf {i}} −4 \ cos t \, \ hat {\ mathbf {j}}} {4} \\[4pt] &=− \sin t\,\hat{\mathbf{i}}− \cos t\,\hat{\mathbf{j}}.\end{align*}\]
Ensuite, nous utilisons\(\ref{EqNormal}\) :
\ [\ begin {align*} \ vecs N (t) &= \ dfrac {\ vecs T' (t)} {« \ vecs T' (t)} \ \ [4pt] &= \ dfrac {− \ cos t \, \ hat {\ mathbf {i}} + \ sin t \, \ hat {\ mathbf {j}}} {\ mathbf {j}} {\ sqrt {(− \ cos t) ^2+ (\ sin t) ^2}} \ \ [4pt]
&= \ dfrac {− \ cos t \, \ hat {\ mathbf {i}} + \ sin t \, \ hat {\ mathbf {j}}} {\ sqrt {\ cos ^2 t+ \ sin ^2 t}} \ \ [4 points]
&=− \ cos t \, \ hat {\ mathbf {i}} + \ sin t \, \ hat {\ mathbf {j}}. \ end {align*} \]
Notez que le vecteur de tangente unitaire et le vecteur normal de l'unité principale sont orthogonaux l'un à l'autre pour toutes les valeurs de\(t\) :
\[\begin{align*} \vecs T(t)·\vecs N(t) &=⟨− \sin t,− \cos t⟩·⟨− \cos t, \sin t⟩ \\[4pt] &= \sin t \cos t−\cos t \sin t \\[4pt] &=0. \end{align*}\]
De plus, le vecteur normal de l'unité principale pointe vers le centre du cercle à partir de chaque point du cercle. Comme\(\vecs r(t)\) définit une courbe en deux dimensions, nous ne pouvons pas calculer le vecteur binormal.
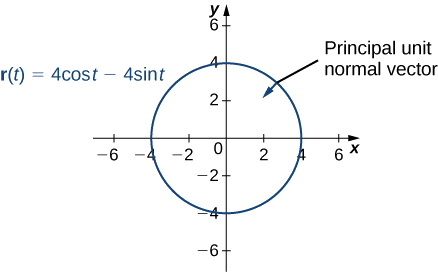
- Cette fonction se présente comme suit :
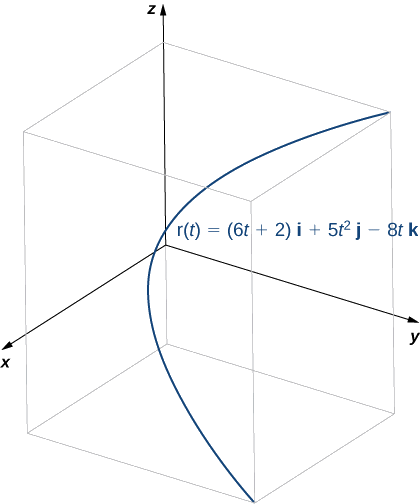
Pour trouver le vecteur normal unitaire principal, nous trouvons d'abord le vecteur tangent unitaire\(\vecs T(t):\)
\ [\ begin {align*} \ vecs T (t) &= \ dfrac {\ vecs r′ (t)} {] \ vecs r′ (t)} \ \ [4pt]
&= \ dfrac {6 \, \ hat {\ mathbf {i}} +10t \, \ hat {\ mathbf {j}} −8 \, \ hat {\ mathbf {j}} −8 \, \ hat {\ mathbf {j}} bf {k}}} {\ sqrt {6^2+ (10t) ^2+ (−8) ^2}} \ \ [4 points]
&= \ dfrac {6 \, \ hat {\ mathbf {i}} +10t \, \ hat {\ mathbf {j}} −8 \, \ hat {\ mathbf {k}}} {\ sqrt {36+j}} 100 t^2+64 }} \ \ [4 points]
&= \ dfrac {6 \, \ hat {\ mathbf {i}} +10t \, \ hat {\ mathbf {j}} −8 \, \ hat {\ mathbf {k}}} {\ sqrt {100 (t^2+1)}} \ \ [4 points]
&= \ dfrac {3 \, \ {\ chapeau mathbf {i}} −5t \, \ hat {\ mathbf {j}} −4 \, \ hat {\ mathbf {k}}} {5 \ sqrt {t^2+1}} \ \ [4pt]
&= \ dfrac {3} {5} (t^2+1) ^ {−1/2} \, \ hat {\ mathbf {i}} −t (t^2) +1) ^ {−1/2} \, \ hat {\ mathbf {j}} − \ dfrac {4} {5} (t^2+1) ^ {−1/2} \, \ hat {\ mathbf {k}}. \ end {align*} \]
Ensuite, nous calculons\(\vecs T′(t)\) et\(‖\vecs T′(t)‖\) :
\ [\ begin {align*} \ vecs T' (t) &= \ dfrac {3} {5} (− \ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t) \, \ hat {\ mathbf {i}} − ((t^2+1) ^ {−1/2} −t (\ dfrac {1} {2}}) (t^2+1) ^ {−3/2} (2t)) \, \ hat {\ mathbf {j}} − \ dfrac {4} {5} (− \ dfrac {1} {2}) (t^2+1) ^ {−3/2} (2t) \, \ hat {\ mathbf {k}} \ \ [4 points]
&=− \ \ dfrac {3t} {5 (t^2+1) ^ {3/2}} \, \ hat {\ mathbf {i}} − \ dfrac { 1} {(t^2+1) ^ {3/2}} \, \ hat {\ mathbf {j}} + \ dfrac {4t} {5 (t^2+1) ^ {3/2}} \, \ hat {\ mathbf {k}} \ \ [4 points], \ vecs T' (t) ※ &= \ sqrt {\ bigg (− \ dfrac) {3t} {5 (t^2+1) ^ {3/2}} \ bigg) ^2+ \ bigg (− \ dfrac {1} {(t^2+1) ^ {3/2}} \ bigg) ^2+ \ bigg (\ dfrac {4t} {5 (t^2+1) ^ {3/2}} \ bigg) ^2} \ \ [4pt]
&&= \ sqrt {\ dfrac {9t^2} {25 (t^2+1) ^3} + \ dfrac {1} {(t^2+1) ^3} + \ dfrac {16t^2} {25 (t^2+1) ^3}} \ \ [4 points]
&= \ sqrt {\ dfrac {25t^2+25} {25 (t^2+1) ^3}} \ \ [4 points]
&= \ sqrt {\ dfrac {1} (t^2+1) ^2}} \ \ [4 points]
&= \ dfrac {1} {t^2+1}. \ end {align*} \]
Par conséquent, selon\(\ref{EqNormal}\) :
\ [\ begin {align*} \ vecs N (t) &= \ dfrac {\ vecs T' (t)} {« \ vecs T' (t)} \ \ [4pt]
&= \ bigg (− \ dfrac {3t} {5 (t^2+1) ^ {3/2}} \, \ hat {\ mathbf {i}} − \ dfrac {2+1) ^ {3/2}} \, \ hat {\ mathbf {i}} − \ dfrac {2+1) ^ {3/2}} \ ac {1} {(t^2+1) ^ {3/2}} \, \ hat {\ mathbf {j}} + \ dfrac {4t} {5 (t^2+1) ^ {3/2}} \, \ hat {\ mathbf {k}} \ bigg) (t^2+1) \ \ [4pt]
&=− \ dfrac {3t} {5 (t^2+1) ^ {1/2}} \, \ hat {\ mathbf {i}} − \ dfrac {5} {5 (t^2+1) ^ {1/2}} \, \ hat {\ mathbf {j}} + \ dfrac {4t} {5 (t^2+1) ^ {1/2}} \, \ hat {\ mathbf {k}} \ \ [4pt]
&=− \ dfrac {3t] \, \ hat {\ mathbf {i}} +5 \, \ hat {\ mathbf {j}} −4t \, \ hat {\ mathbf {k}}} {5 \ sqrt {t^2+1}}. \ end {align*} \]
Encore une fois, le vecteur tangent unitaire et le vecteur normal unitaire principal sont orthogonaux l'un à l'autre pour toutes les valeurs de\(t\) :
\ [\ begin {align*} \ vecs T (t) · \ vecs N (t) &= \ bigg (\ dfrac {3 \, \ hat {\ mathbf {i}} −5t \, \ hat {\ mathbf {j}} −4 \, \ hat {\ mathbf {k}}} {5 \ sqrt {t^2+1}} \ bigg) · \ bigg (− \ dfrac {3t \, \ hat {\ mathbf {i}} +5 \, \ hat {\ mathbf {j}} −4t \, \ hat {\ mathbf {k}}} {5 \ sqrt {t^2+1}} \ bigg) \ \ [4 points] &= \ dfrac {3 (−3t) −5+1}} \ bigg) \ \ [4 points]
&= \ dfrac {3 (−3) −5 t (−5) −4 (4)} {25 (t^2+1)} \ \ [4 points]
&= \ dfrac {−9t+25 t−16 t} {25 (t^2+1)} \ \ [4 points]
&=0. \ end {align*} \ nonumber \]
Enfin, comme il s'\(\vecs r(t)\)agit d'une courbe tridimensionnelle, nous pouvons calculer le vecteur binormal en utilisant\(\ref{EqBinormal}\) :
\ [\ begin {align*} \ vecs B (t) &= \ ; \ vecs T (t) × \ vecs N (t) \ \ [4pt]
&= \ begin {vmatrix} \ hat {\ mathbf {i}} & \ hat {\ mathbf {j}} & \ hat {\ mathbf {k}} \ \ dfrac {3} {5 \ sqrt {t^2+1}} & − \ dfrac {5t} {5 \ sqrt {t^2+1}} & − \ dfrac {4} {5 \ sqrt {t^2+1}} \ \ − \ dfrac {3t} {5 \ sqrt {t^2+1}} & − \ dfrac {5} {5 \ sqrt {t^2+1}} & \ dfrac {4t} {5 \ sqrt {t^2+1}} \ end {vmatrix} \ \ [4pt]
&= \ bigg (\ bigg (− \ dfrac {5t} {5 \ sqrt {t^2+1}} \ bigg) \ bigg (\ dfrac {4t} {5 \ sqrt {t^2+1}} \ bigg) − \ bigg (− \ dfrac {4} {5 \ sqrt {t^2+1}} \ bigg) \ bigg (− \ dfrac {5} {5} \ sqrt {t^2+1}} \ bigg) \, \ hat {\ mathbf {i}} \ \
& - \ bigg (\ bigg (\ dfrac {3} {5 \ sqrt {t^2+1}} \ bigg) \ bigg (\ dfrac {4t} {5 \ sqrt {t^2+1}} \ bigg) − \ bigg (− \ dfrac {4} {5 \ sqrt {t^2+1}} \ bigg) \ bigg (\ dfrac {3t} {5 \ sqrt {t^2+1}} \ bigg) \, \ hat {\ mathbf {j}} \ \
& + \ bigg (\ bigg (\ dfrac {3} {5 \ sqrt {t^2+1}} \ bigg) \ bigg (- \ dfrac {5} {5} {5 \ sqrt ^2+1}} \ bigg) − \ bigg (− \ dfrac {5t} {5 \ sqrt {t^2+1}} \ bigg) \ bigg (− \ dfrac {3t} {5 \ sqrt {t^2+1}} \ bigg) \, \ hat {\ mathbf {k}} \ \ [4pt]
&= \ bigg (\ dfrac {−20t^2−20} {25 (t^2+1)} \ bigg) \, \ hat {\ mathbf {i}} + \ bigg (\ dfrac {−15−15t^2} {25 (t^2+1)} \ bigg) \, \ hat {\ mathbf {k}} \ \ [4 points]
&= −20 \ bigg (\ dfrac {t^2+1} {25 (t^2+1)} \ bigg) \, \ hat {\ mathbf {i}} −15 \ bigg (\ dfrac {t^2+1}} {25 (t^2+1)} \ bigg) \, \ hat {\ mathbf {k}} \ \ [4 points]
&= − \ dfrac {4} {5} \, \ hat {\ mathbf {i}} − \ dfrac {3} {5} \, \ hat {\ mathbf {k}}. \ end {align*} \ nonumber \]
Trouvez le vecteur normal unitaire pour la fonction à valeur vectorielle\(\vecs r(t)=(t^2−3t)\,\hat{\mathbf{i}}+(4t+1)\,\hat{\mathbf{j}}\) et évaluez-le à\(t=2\).
- Allusion
-
Tout d'abord, trouvez\(\vecs T(t)\), puis utilisez\(\ref{EqNormal}\).
- Réponse
-
\(\vecs N(2)=\dfrac{\sqrt{2}}{2}(\,\hat{\mathbf{i}}−\,\hat{\mathbf{j}})\)
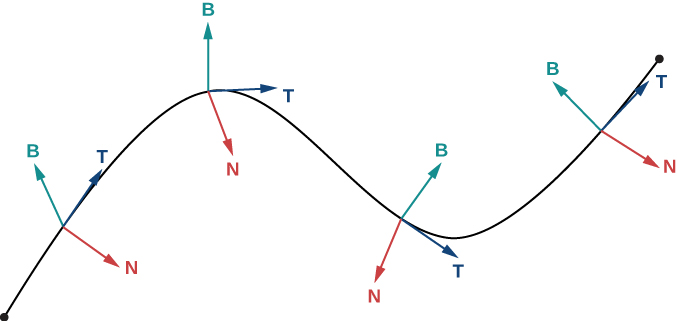
Pour toute courbe lisse en trois dimensions définie par une fonction à valeur vectorielle, nous avons maintenant des formules pour le vecteur tangente unitaire\(\vecs T\), le vecteur\(\vecs N\) normal unitaire et le vecteur binormal\(\vecs B\). Le vecteur normal unitaire et le vecteur binormal forment un plan perpendiculaire à la courbe en tout point de la courbe, appelé plan normal. De plus, ces trois vecteurs forment un cadre de référence dans l'espace tridimensionnel appelé référentiel Frenet (également appelé cadre TNB) (Figure\(\PageIndex{2}\)). Enfin, le plan déterminé par les vecteurs\(\vecs T\) et\(\vecs N\) forme le plan osculant de n'\(C\)importe quel point de\(P\) la courbe.
Supposons que nous formions un cercle dans le plan osculant d'\(C\)\(P\)au point de la courbe. Supposons que le cercle ait la même courbure que la courbe au point\(P\) et que le cercle ait un rayon\(r\). Ensuite, la courbure du cercle est donnée par\(\frac{1}{r}\). Nous appelons\(r\) le rayon de courbure de la courbe, et il est égal à l'inverse de la courbure. Si ce cercle se trouve sur le côté concave de la courbe et qu'il est tangent à la courbe en un point\(P\), alors ce cercle est appelé cercle osculant de\(C\) at\(P\), comme indiqué sur la figure\(\PageIndex{3}\).
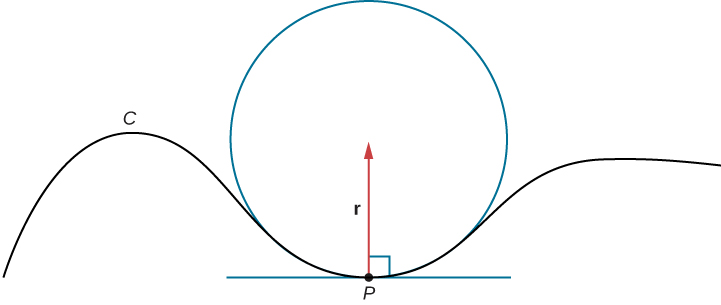
Pour plus d'informations sur les cercles osculants, voir cette démonstration sur la courbure et la torsion, cet article sur les cercles osculants et cette discussion sur les formules de Serret.
Pour trouver l'équation d'un cercle osculant en deux dimensions, il suffit de trouver le centre et le rayon du cercle.
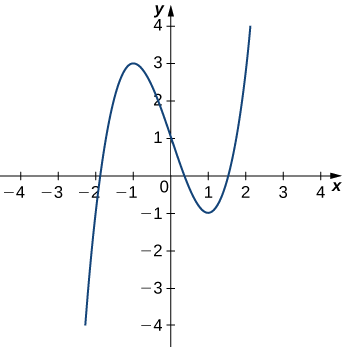
Détermine l'équation du cercle osculant de la courbe définie par la fonction\(y=x^3−3x+1\) at\(x=1\).
Solution
La figure\(\PageIndex{4}\) montre le graphique de\(y=x^3−3x+1\).
Tout d'abord, calculons la courbure à\(x=1\) :
\[κ =\dfrac{|f″(x)|}{\bigg( 1+[f′(x)]^2 \bigg) ^{3/2}} = \dfrac{|6x|}{(1+[3x^2−3]^2)^{3/2}}. \nonumber \]
Cela donne\(κ=6\). Par conséquent, le rayon du cercle osculant est donné par\(R=\frac{1}{κ}=\dfrac{1}{6}\). Ensuite, nous calculons les coordonnées du centre du cercle. Lorsque\(x=1\), la pente de la tangente est nulle. Par conséquent, le centre du cercle osculant se trouve directement au-dessus du point du graphique avec ses coordonnées\((1,−1)\). Le centre est situé à\((1,−\frac{5}{6})\). La formule pour un cercle avec rayon\(r\) et centre\((h,k)\) est donnée par\((x−h)^2+(y−k)^2=r^2\). Par conséquent, l'équation du cercle osculant est\((x−1)^2+(y+\frac{5}{6})^2=\frac{1}{36}\). Le graphe et son cercle osculant apparaissent dans le graphique suivant.
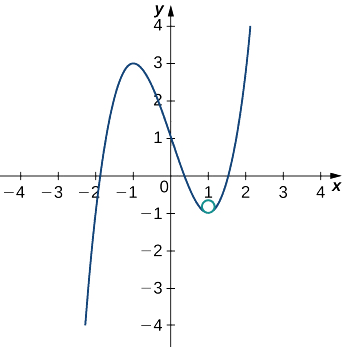
Trouvez l'équation du cercle osculant de la courbe définie par la fonction\(y=2x^2−4x+5\) à valeur vectorielle à\(x=1\).
- Allusion
-
\(\ref{EqK4}\)Utilisez-le pour trouver la courbure du graphique, puis dessinez un graphique de la fonction environnante\(x=1\) pour vous aider à visualiser le cercle par rapport au graphique.
- Réponse
-
\(κ =\frac{4}{[1+(4x−4)^2]^{3/2}}\)
Au point\(x=1\), la courbure est égale à\(4\). Par conséquent, le rayon du cercle osculant est\(\frac{1}{4}\).
Un graphique de cette fonction apparaît ensuite :
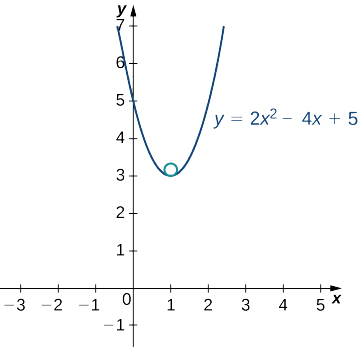
Le sommet de cette parabole est situé au point\((1,3)\). De plus, le centre du cercle osculant se trouve directement au-dessus du sommet. Par conséquent, les coordonnées du centre sont\((1,\frac{13}{4})\). L'équation du cercle osculant est
\((x−1)^2+(y−\frac{13}{4})^2=\frac{1}{16}\).
Concepts clés
- La fonction de longueur d'arc pour une fonction à valeur vectorielle est calculée à l'aide de la formule intégrale\(\displaystyle s(t)=\int_a^b ‖\vecs r′(t)‖\,dt \). Cette formule est valable en deux et en trois dimensions.
- La courbure d'une courbe en un point en deux ou trois dimensions est définie comme étant la courbure du cercle inscrit à ce point. Le paramétrage de la longueur de l'arc est utilisé dans la définition de la courbure.
- Il existe différentes formules pour la courbure. La courbure d'un cercle est égale à l'inverse de son rayon.
- Le vecteur normal unitaire principal at\(t\) est défini comme étant
\[\vecs N(t)=\dfrac{\vecs T′(t)}{‖\vecs T′(t)‖}. \nonumber \]
- Le vecteur binormal at\(t\) est défini comme\(\vecs B(t)=\vecs T(t)×\vecs N(t)\), où\(\vecs T(t)\) est le vecteur tangent unitaire.
- Le cadre de référence Frenet est formé par le vecteur tangent unitaire, le vecteur normal unitaire principal et le vecteur binormal.
- Le cercle osculant est tangent à une courbe en un point et possède la même courbure que la courbe tangente à ce point.
Équations clés
- Longueur de l'arc de la courbe spatiale
\(s= {\displaystyle \int _a^b} \sqrt{[f′(t)]^2+[g′(t)]^2+[h′(t)]^2} \,dt= {\displaystyle \int _a^b} ‖\vecs r′(t)‖\,dt\) - Fonction de longueur d'arc
\(s(t)={\displaystyle \int _a^t} \sqrt{f′(u))^2+(g′(u))^2+(h′(u))^2} \,du \; or \; s(t)={\displaystyle \int _a^t}‖\vecs r′(u)‖\,du\) - \(κ=\frac{‖\vecs T′(t)‖}{‖\vecs r′(t)‖} \; or \; κ=\frac{‖\vecs r′(t)×\vecs r″(t)‖}{‖\vecs r′(t)‖^3} \; or \; κ=\frac{|y″|}{[1+(y′)^2]^{3/2}}\)
- Vecteur normal de l'unité principale
\(\vecs N(t)=\frac{\vecs T′(t)}{‖\vecs T′(t)‖}\) - Vecteur binormal
\(\vecs B(t)=\vecs T(t)×\vecs N(t)\)
Lexique
- fonction de longueur d'arc
- une fonction\(s(t)\) qui décrit la longueur de l'arc de la courbe\(C\) en fonction de\(t\)
- paramétrage de la longueur de l'arc
- un reparamétrage d'une fonction à valeur vectorielle dans laquelle le paramètre est égal à la longueur de l'arc
- vecteur binormal
- un vecteur unitaire orthogonal au vecteur tangent unitaire et au vecteur normal unitaire
- courbure
- la dérivée du vecteur tangent unitaire par rapport au paramètre de longueur de l'arc
- Cadre de référence Frenet
- (trame TNB) un cadre de référence dans un espace tridimensionnel formé par le vecteur tangent unitaire, le vecteur normal unitaire et le vecteur binormal
- plan normal
- un plan perpendiculaire à une courbe en tout point de la courbe
- cercle osculant
- un cercle tangent à une courbe\(C\) en un point\(P\) et qui partage la même courbure
- plan osculant
- le plan déterminé par la tangente unitaire et le vecteur normal unitaire
- vecteur normal de l'unité principale
- un vecteur orthogonal au vecteur tangent unitaire, donné par la formule\(\frac{\vecs T′(t)}{‖\vecs T′(t)‖}\)
- rayon de courbure
- l'inverse de la courbure
- lisse
- courbes où la fonction à valeur vectorielle\(\vecs r(t)\) est dérivable avec une dérivée non nulle


