13.2E : Exercices pour la section 13.2

Last updated
Save as PDF

Page ID: 197232

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Prendre des dérivées de fonctions à valeur vectorielle

Dans les questions 1 à 10, calculez la dérivée de chaque fonction à valeur vectorielle.

1)$\vecs r(t)=t^3 \,\hat{\mathbf{i}}+3t^2 \,\hat{\mathbf{j}}+\dfrac{t^3}{6}\,\hat{\mathbf{k}}$

Réponse: $\vecs r'(t)= 3t^2 \,\hat{\mathbf{i}}+6t\,\hat{\mathbf{j}}+\frac{1}{2}t^2\,\hat{\mathbf{k}}$

2)$\vecs r(t)=\sin(t) \,\hat{\mathbf{i}}+\cos(t) \,\hat{\mathbf{j}}+e^t \,\hat{\mathbf{k}}$

3)$\vecs r(t)=e^{−t} \,\hat{\mathbf{i}}+\sin(3t) \,\hat{\mathbf{j}}+10 \sqrt{t} \,\hat{\mathbf{k}}$. Un croquis du graphique est présenté ici. Remarquez la nature périodique variable du graphique.

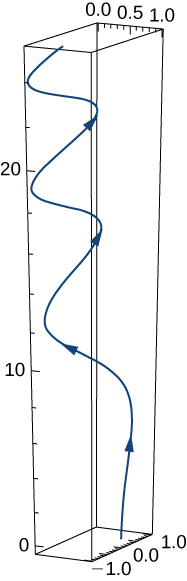
$Graphique de la trajectoire 3D du tire-bouchon de r (t) =e^ (−t) i+ sin (3t) j+10 sqrt (t) k.$

Réponse: $\vecs r'(t) = −e^{−t}\,\hat{\mathbf{i}}+3\cos (3t)\,\hat{\mathbf{j}}+\dfrac{5}{\sqrt{t}}\,\hat{\mathbf{k}}$

4)$\vecs r(t)=e^t \,\hat{\mathbf{i}}+2e^t \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$

5)$\vecs r(t)=\,\hat{\mathbf{i}}+\,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$

Réponse: $\vecs r'(t) = ⟨0,0,0⟩ = \vecs 0$

6)$\vecs r(t)=te^t \,\hat{\mathbf{i}}+t \ln(t) \,\hat{\mathbf{j}}+\sin(3t)\,\hat{\mathbf{k}}$

7)$\vecs r(t)=\left\langle\dfrac{1}{t+1},\,\arctan(t), \,\ln t^3 \right\rangle$

Réponse: $\vecs r'(t) = ⟨\dfrac{−1}{(t+1)^2},\dfrac{1}{1+t^2},\dfrac{3}{t}⟩$

8)$\vecs r(t)= \langle\tan 2t, \,\sec 2t, \,\sin ^2 t\rangle$

9)$\vecs r(t)=\langle 3,\, 4 \sin (3t),\, t \cos(t)\rangle$

Réponse: $\vecs r'(t) = ⟨0,12 \cos(3t), \cos t−t \sin t⟩$

10)$\vecs r(t)=t^2 \,\hat{\mathbf{i}}+te^{−2t} \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}$

11) a. Décrivez et esquissez la courbe représentée par la fonction à valeur vectorielle$\vecs r(t)=⟨6t,6t−t^2⟩$.

b. Localisez le point le plus haut de la courbe$\vecs r(t)=⟨6t,6t−t^2⟩$ et donnez la valeur de la fonction à ce point.

Réponse: b.$\vecs r(t)=⟨18,9⟩$ à$ t=3$

12) Trouvez les équations paramétriques de la tangente à la courbe$\vecs r(t)=⟨t, t^2,t⟩$ à$t=2$.

13) Trouvez les équations paramétriques de la tangente à la courbe$\vecs r(t)=⟨e^t,e^{−t},0⟩$ à$t=0$.

Réponse: $x=1+t,\quad y=1−t,\quad z=0$

14) Calculez les première, deuxième et troisième dérivées de$\vecs r(t)=3t \,\hat{\mathbf{i}}+6\ln(t) \,\hat{\mathbf{j}}+5e^{−3t}\,\hat{\mathbf{k}}$.

Décrire le mouvement à l'aide de fonctions à valeurs vectorielles

Dans les questions 15 à 17, trouvez la vitesse et l'accélération aux moments donnés, tracez le graphique de la fonction de position et tracez les vecteurs de vitesse et d'accélération aux emplacements correspondants sur la courbe.

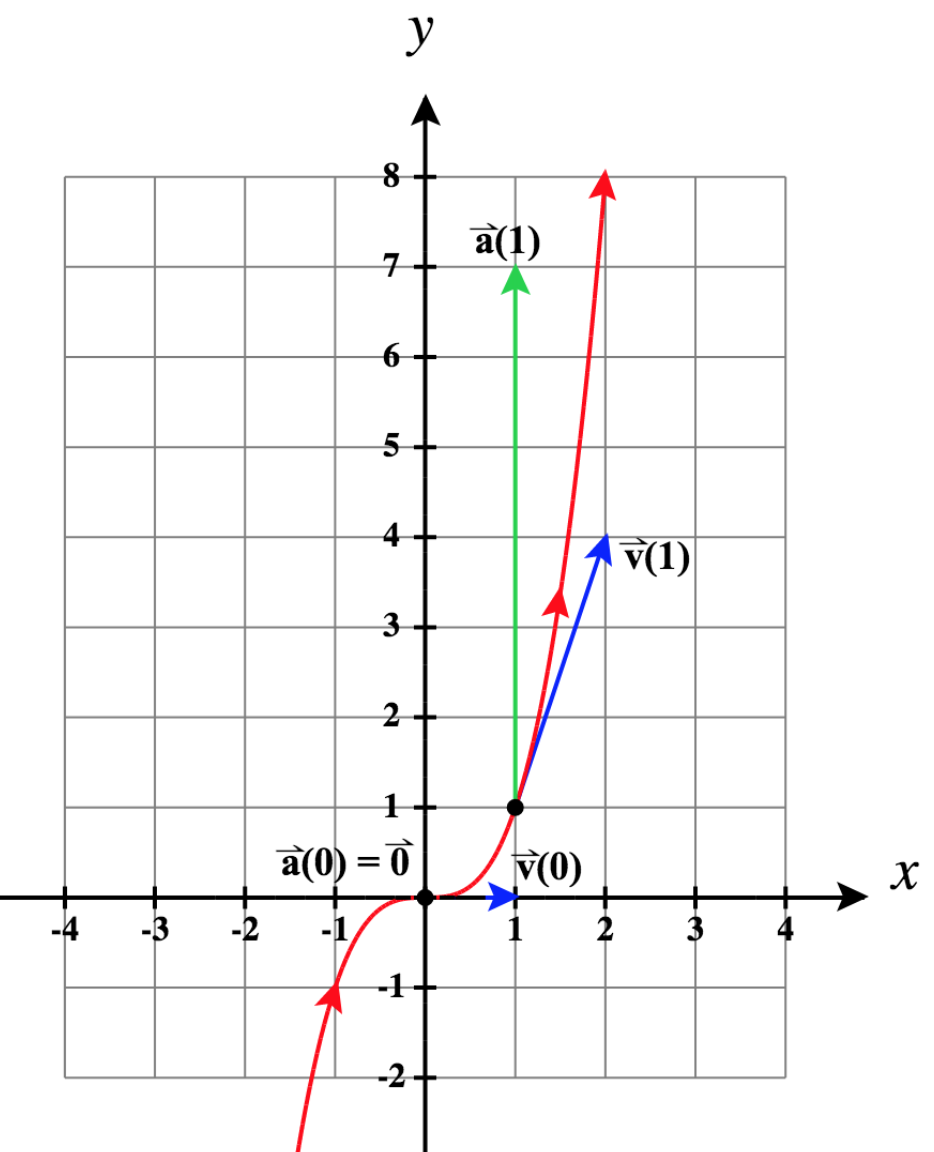
15)$\vecs r(t)= t \,\hat{\mathbf{i}}+t^3\,\hat{\mathbf{j}}$, à$t = 0$ et à$t = 1$

Réponse: \ (\ begin {array} {lll} \, & t = 0 : & t = 1 : \ \
\ vecs r (t) = t \, \ mathbf {\ hat i} + t^3 \, \ mathbf {\ hat j}, & \ vecs r (0) = \ vecs 0, & \ vecs r (1) = \ mathbf {\ hat i} + mathbf {\ hat j} \ \
\ vecs v (t) = \ mathbf {\ hat i} + 3t^2 \, \ mathbf {\ hat j}, & \ vecs v (0) = \ mathbf {\ hat i}, & \ vecs v (1) = \ mathbf {\ hat i} + 3 \, \ mathbf {\ hat j} \ \
\ vecs a (t) = 6t \, \ mathbf {\ hat j}, & \ vecs a (0) = \ vecs 0, & \ vecs a (1) = 6 \, \ mathbf {\ hat j} \ end {tableau} \)
$Tracé le long du graphe de y = x^3 de gauche à droite. Affichage des vecteurs de vitesse et d'accélération à t = 0 et t = 1.$

16)$\vecs r(t)= \cos t \,\hat{\mathbf{i}}+\sin 3t \,\hat{\mathbf{j}}$, à$t = 0$$t = \frac{\pi}{4}$, à et à$t = \frac{\pi}{2}$

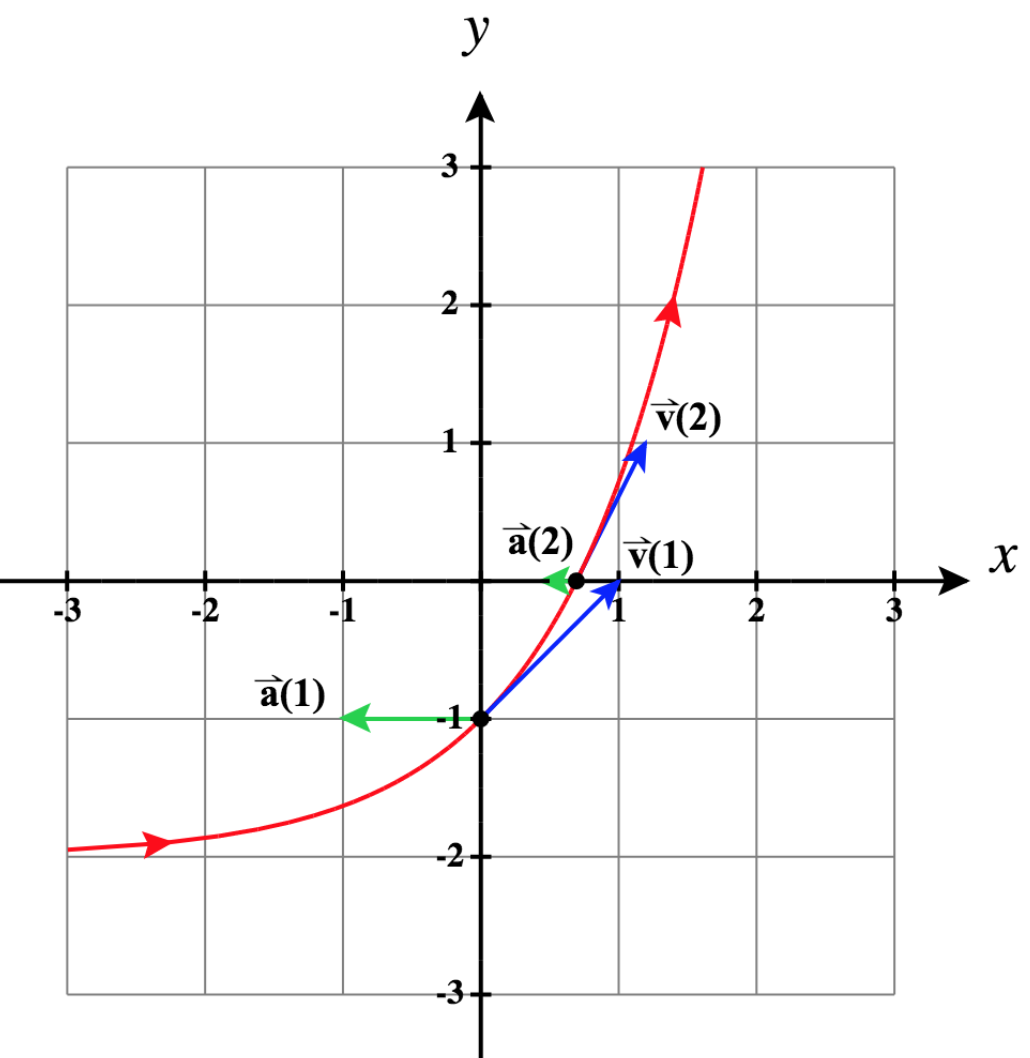
17)$\vecs r(t)= \ln t \,\hat{\mathbf{i}}+(t-2)\,\hat{\mathbf{j}}$, à$t = 1$ et à$t = 2$

Réponse: \ (\ begin {array} {lll} \, & t = 1 : & t =2 : \ \
\ vecs r (t) = (\ ln t) \, \ mathbf {\ hat i} + (t - 2) \, \ mathbf {\ hat j}, & \ vecs r (1) = - \ mathbf {\ hat j}, & \ vecs r (2) = (\ ln 2) \, \ mathbf {\ hat i} \ \
\ vecs v (t) = \ dfrac {1} {t} \, \ mathbf {\ hat i} + \ mathbf {\ hat j}, & \ vecs v (1) = \ mathbf {\ hat i} + \ mathbf {\ hat j}, & \ vecs v (2) = \ frac {1} {2} \ mathbf {\ hat i} + \ mathbf {\ hat j} \ \
\ vecs a (t) = - \ dfrac {1} {t^2} \, \ mathbf {\ hat i}, & \ vecs a (1) = - \ mathbf {\ hat i}, & \ vecs a (2) = - \ frac {1} {4} \, \ mathbf {\ hat i} \ end {tableau} \)
$Trajet le long du graphe de r (t) = ln (t) i + (t - 2) j. Affichage des vecteurs de vitesse et d'accélération à t = 1 et t = 2.$

Dans les questions 18 à 24, déterminez la vitesse, la vitesse et l'accélération d'une particule avec la fonction de position donnée. N'oubliez pas que la vitesse est l'amplitude de la vitesse représentée par$‖\vecs v(t)‖$ ou$‖\vecs r′(t)‖$.

18)$\vecs r(t)=e^{2t} \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}$

19)$\vecs r(t)=\cos t^3 \,\hat{\mathbf{i}}+\sin t^3 \,\hat{\mathbf{j}}$

Réponse: $\vecs v(t)=-3t^2\sin t^3 \,\hat{\mathbf{i}}+3t^2\cos t^3 \,\hat{\mathbf{j}}, \quad \text{speed}(t)=‖\vecs v(t)‖=3t^2, \quad \vecs a(t) = \left( -6t\sin t^3 - 9t^4\cos t^3 \right) \,\hat{\mathbf{i}}+\left( 6t\cos t^3 - 9t^4\sin t^3 \right) \,\hat{\mathbf{j}}$

20)$\vecs r(t)=⟨e^t,e^{−t},0⟩$

(21)$\vecs r(t)=⟨t+ \cos t,t− \sin t⟩$

Réponse: $\vecs v(t)=⟨1− \sin t,1−\cos t⟩, \quad \text{speed}(t)=‖\vecs v(t)‖=\sqrt{3−2( \sin t+\cos t)}, \quad \vecs a(t) = ⟨- \cos t, \sin t⟩$

22)$\vecs r(t)=\dfrac{2t−1}{2t+1} \,\hat{\mathbf{i}}+\ln(1−4t^2) \,\hat{\mathbf{j}}$

23)$\vecs r(t)=\cos 3t \,\hat{\mathbf{i}}+\sin 3t \,\hat{\mathbf{j}} + 0.5t \,\hat{\mathbf{k}} $

Réponse: $\vecs v(t)=-3\sin 3t \,\hat{\mathbf{i}}+3\cos 3t \,\hat{\mathbf{j}} +0.5 \,\mathbf{\hat k}, \quad \text{speed}(t)=‖\vecs v(t)‖=\sqrt{9.25}\text{ units/sec}, \quad \vecs a(t) = -9\cos 3t \,\hat{\mathbf{i}}-9\sin 3t \,\hat{\mathbf{j}}$

(24)$\vecs r(t)=e^{-t} \,\hat{\mathbf{i}}+(\ln t) \,\hat{\mathbf{j}}+(\sin 7t)\,\hat{\mathbf{k}}$

25) Considérez le vecteur de position d'une particule$\vecs r(t)=t \,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+t^3 \,\hat{\mathbf{k}}$. Le graphique est présenté ici :

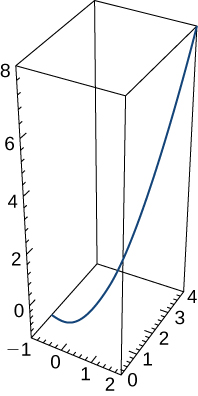
a. Trouvez le vecteur de vitesse à tout moment.

b. Détermine la vitesse de la particule au temps$t=2$ sec.

c. Trouvez l'accélération au temps$t=2$ sec.

Réponse: a.$\vecs v(t)=\hat{\mathbf{i}}+2t\,\hat{\mathbf{j}}+3t^2 \,\hat{\mathbf{k}}$
b.$\sqrt{161}$ unités/sec
Notez que,$\text{speed}(t) = \|\vecs v(t)\| = \sqrt{1^2 + (2t)^2 + (3t^2)^2} = \sqrt{1 + 4t^2 + 9t^4}.$
par conséquent,$\text{speed}(2) = \sqrt{1 + 16 + 9(16)} = \sqrt{161}$ unités/sec.
c. Depuis$\vecs a(t)=2\,\hat{\mathbf{j}}+6t \,\hat{\mathbf{k}},$$\vecs a(2) = 2\,\hat{\mathbf{j}}+12 \,\hat{\mathbf{k}}$

26) Une particule se déplace le long de la trajectoire d'une ellipse avec l'équation$\vecs r(t)=\cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$. Trouvez ce qui suit :

a. Vitesse de la particule

Réponse: $\vecs v(t)=⟨−\sin t,2 \cos t,0⟩$

b. Vitesse de la particule à$t=\frac{π}{4}$

c. Accélération de la particule à$t=\frac{π}{4}$

Réponse: $\vecs a(t)=⟨−\frac{\sqrt{2}}{2},−\sqrt{2},0⟩$

27) Montrez que si la vitesse d'une particule se déplaçant le long d'une courbe représentée par une fonction à valeur vectorielle est constante, la fonction de vitesse est toujours perpendiculaire à la fonction d'accélération.

Réponse: $\begin{align*} ‖\vecs v(t)‖ \; & = k \\ \vecs v(t)·\vecs v(t) \; & = k^2 \\ \frac{d}{dt}\Big(\vecs v(t)·\vecs v(t)\Big) \; & =\frac{d}{dt}\Big(k^2\Big)=0 \\ \vecs v(t)·\vecs v′(t)+\vecs v′(t)·\vecs v(t) \; & = 0 \\ 2\vecs v(t)·\vecs v′(t) \; & =0 \\ \vecs v(t)·\vecs v′(t) \; & = 0\end{align*}$

La dernière déclaration implique que la vitesse et l'accélération sont perpendiculaires ou orthogonales.

28) Compte tenu de la fonction à valeur vectorielle$\vecs r(t)=⟨\tan t,\sec t,0⟩$ (le graphique est illustré ici), trouvez ce qui suit :

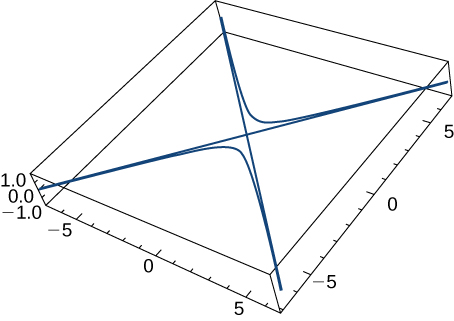
a. Vélocité

Réponse: $\vecs v(t)=\langle \sec ^2 t,\,\sec t \tan t\rangle$

b. Vitesse

Réponse: $‖\vecs v(t)‖=\sqrt{\sec ^4 t+\sec ^2 t \tan ^2 t}=\sqrt{(\sec ^2 t)(\sec ^2 t+\tan ^2 t)}$

c. Accélération

Réponse: $\vecs a(t)=\langle 2\sec ^2 t\tan t,\,\sec t \tan^2 t+\sec^3 t\rangle$

29) Déterminez la vitesse minimale d'une particule se déplaçant le long de la courbe$\vecs r(t)=⟨t+\cos t,t−\sin t⟩$, où$t∈[0,2π)$. Ensuite, trouvez également sa vitesse maximale sur cet intervalle.

Réponse: La vitesse minimale, c'est$\sqrt{3-2\sqrt{2}}\approx 0.41421$ quand$t=\tfrac{\pi}{4}$.
La vitesse maximale est$\sqrt{3+2\sqrt{2}}\approx 2.41421$ quand$t=\tfrac{5\pi}{4}$.

Pour les questions 30 à 31, considérez une particule qui se déplace sur une trajectoire circulaire de rayon$b$ selon la fonction$\vecs r(t)=b \cos(\omega t) \,\hat{\mathbf{i}}+b\sin(\omega t) \,\hat{\mathbf{j}}$, où$\omega$ est la vitesse angulaire,$\dfrac{d \theta}{dt}$.

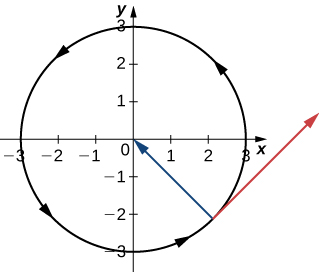
30) Montrez que la vitesse de la particule est proportionnelle à la vitesse angulaire.

31) Trouvez la fonction de vitesse et montrez qui$\vecs v(t)$ est toujours orthogonale à$\vecs r(t)$.

Réponse: $\vecs r'(t)=−b \omega \sin( \omega t)\,\hat{\mathbf{i}}+b \omega \cos(\omega t)\,\hat{\mathbf{j}}$. Pour montrer l'orthogonalité, notez que$\vecs r'(t)⋅\vecs r(t)=0$.

Fluidité des fonctions à valeur vectorielle

Pour les questions 32 à 40,

a. Déterminez toutes les valeurs dont$t$ la valeur n'$\vecs r$est pas uniforme.

b. Déterminez les intervalles ouverts sur lesquels$\vecs r$ est lisse.

c. Représentez graphiquement la fonction à valeur vectorielle et décrivez son comportement aux points où elle n'est pas lisse.

32)$\vecs r(t) = \langle 3t, 5t^2 - 1\rangle$

33)$\vecs r(t)= t^3\,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}$

Réponse: a. n'$\vecs r$est pas fluide à$t = 0$, puisque$\vecs r'(0) = \vecs 0$.
b.$\vecs r$ est lisse sur les intervalles ouverts$(-\infty, 0)$ et$(0, \infty)$.
c. Il y a un moment où$t = 0$.

34)$\vecs r(t)=\langle 5,\, 2 \sin (t),\, \cos(t)\rangle$

35)$\vecs r(t) = \langle t^3 - 3t^2, 7\rangle$

Réponse: a. n'$\vecs r$est pas fluide à$t = 0$ et$t = 2$, depuis$\vecs r'(0) = \vecs 0$ et$\vecs r'(2) = \vecs 0$.
b.$\vecs r$ est lisse sur les intervalles ouverts$(-\infty, 0)$$(0, 2)$, et$(2, \infty)$.
c. Le mouvement sur la courbe s'inverse le long de la même trajectoire à la fois$t = 0$ et$t = 2$.

36)$\vecs r(t)=t^2 \,\hat{\mathbf{i}}+t^3 \,\hat{\mathbf{j}}−5e^{−4t} \,\hat{\mathbf{k}}$

37)$\vecs r(t)=\left\langle \ln(t^2+4t+5), \,\dfrac{t^3}{3} - 4t,\, 5\right\rangle$

Réponse: a. n'$\vecs r$est pas fluide à$t = -2$, puisque$\vecs r'(-2) = \vecs 0$.
Puisque le domaine$\vecs r$ est$(-\infty, \infty)$, c'est tout ce que nous avons à supprimer.
b.$\vecs r$ est lisse sur les intervalles ouverts$(-\infty, -2)$ et$(-2, \infty)$.
c. Il y a un moment où$t = -2$.

38)$\vecs r(t) = \left( 5\cos t - \cos 5t\right) \,\hat{\mathbf{i}} + \left( 5\sin t - \sin 5t \right) \,\hat{\mathbf{j}}$, pour$0 \le t \le 2\pi$

39)$\vecs r(t)=\sqrt{t^3 + 9t^2} \,\hat{\mathbf{i}}+\left(t^2 +12t\right) \,\hat{\mathbf{j}}+7\,\hat{\mathbf{k}}$

Réponse: a. Le domaine de$\vecs r$ est$[-9, \infty)$.
Et n'$\vecs r$est pas fluide à$t = -6$, puisque$\vecs r'(-6) = \vecs 0$.
Le domaine de$\vecs r'$ est$(-9, \infty)$, puisqu'il n'$\vecs r'$est pas défini à$t = -9$.
b.$\vecs r$ est lisse sur les intervalles ouverts$(-9, -6)$ et$(-6, \infty)$.
c. Il y a un moment où$t = -6$.

40)$\vecs r(t)= \cos^3 t\,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}$, pour$0 \le t \le 2\pi$

Réponse: a. Le domaine de$\vecs r$ est$(-\infty, \infty)$.
$\vecs r'(t) = -3(\cos^2 t)(\sin t)\,\hat{\mathbf{i}}+\cos t \,\hat{\mathbf{j}}$. Son domaine l'est également$(-\infty, \infty)$.
Mais notez que les deux composants ont un facteur de$\cos t$, donc les deux composants seront$0$ quand$\cos t = 0$.
Par conséquent, n'$\vecs r$est pas lisse à$t = \frac{\pi}{2}$ et à$t = \frac{3\pi}{2}$, depuis$\vecs r'\left( \frac{\pi}{2}\right) = \vecs 0$ et$\vecs r'\left( \frac{3\pi}{2}\right) = \vecs 0$. Notez donc que ce n'$\vecs r$est pas lisse pour un multiple impair de$\frac{\pi}{2}$, c'est-à-dire pour$t = \frac{(2n + 1)\pi}{2}$ n'importe quelle valeur entière$n$.
b.$\vecs r$ est lisse sur les intervalles ouverts$\left(\dfrac{(2n - 1)\pi}{2}, \dfrac{(2n + 1)\pi}{2}\right)$, quelle que soit la valeur entière$n$.
c. Il y a un point critique où$t = \dfrac{(2n + 1)\pi}{2}$, pour n'importe quelle valeur entière$n$.

Propriétés du dérivé

Pour les questions 41 à 43, évaluez chaque expression étant donné que$\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}−t^4 \,\hat{\mathbf{k}} $ et$\vecs s(t)=\sin(t) \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+ \cos(t) \,\hat{\mathbf{k}} $

41)$\dfrac{d}{dt}\big[\vecs r(t^2)\big]$

Réponse: $\dfrac{d}{dt}\big[\vecs r(t^2)\big] = ⟨2t,4t^3,−8t^7⟩$

42)$\dfrac{d}{dt}\big[t^2⋅\vecs s(t)\big]$

43)$\dfrac{d}{dt}\big[\vecs r(t)⋅\vecs s(t)\big]$

Réponse: $\dfrac{d}{dt}\big[\vecs r(t)⋅\vecs s(t)\big]=\sin t+2te^t−4t^3 \cos t+t\cos t+t^2e^t+t^4\sin t$

44) Trouvez$\vecs r'(t)⋅\vecs r''(t) \; for \; \vecs r(t)=−3t^5 \,\hat{\mathbf{i}}+5t \,\hat{\mathbf{j}}+2t^2 \,\hat{\mathbf{k}}$.

Réponse: $\vecs r'(t)⋅\vecs r''(t) = 900t^7+16t$

45) Donné$\vecs r(t)=t \,\hat{\mathbf{i}}+3t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}}$ et$\vecs u(t)=4t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t^3 \,\hat{\mathbf{k}}$, trouvez$\frac{d}{dt}(\vecs r(t) \times \vecs u(t))$.

46) Évaluer$\dfrac{d}{dt}\big[\vecs u(t) \times\vecs u′(t)\big]$ donné$\vecs u(t)=t^2 \,\hat{\mathbf{i}}−2t \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$.

Réponse: $\dfrac{d}{dt}\big[\vecs u(t) \times\vecs u′(t)\big] = 0 \,\hat{\mathbf{i}} +2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}$

47) Étant donné$\vecs r(t)=t \,\hat{\mathbf{i}}+2\sin t \,\hat{\mathbf{j}}+2 \cos t \,\hat{\mathbf{k}}$ et$\vecs u(t)=\dfrac{1}{t} \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+2 \cos t \,\hat{\mathbf{k}}$, trouvez ce qui suit :

un.$\vecs r(t) \times \vecs u(t)$

Réponse: $\vecs r(t) \times \vecs u(t) = \left\langle 0, \;2(\cos t)\left(\frac{1}{t}-t\right),\; 2 (\sin t)\left(t- \frac{1}{t}\right)\right\rangle$

b.$\frac{d}{dt}\big(\vecs r(t) \times \vecs u(t)\big)$

Réponse: $\frac{d}{dt}\big(\vecs r(t) \times \vecs u(t)\big) = \left\langle 0, \;2(\sin t)\left(t− \frac{1}{t}\right)−2 (\cos t)\left(1+ \frac{1}{t^2}\right),\;2 \left(\sin t\right)\left(1+ \frac{1}{t^2}\right)+2 \left(\cos t\right)\left(t−\frac{1}{t}\right)\right\rangle$

c. Maintenant, utilisez la règle du produit pour la dérivée du produit croisé de deux vecteurs et montrez que ce résultat est identique à la réponse au problème précédent.

Vecteurs tangents unitaires

Pour les questions 48 à 51, trouvez un vecteur tangent unitaire à la valeur indiquée de$t$.

48)$\vecs r(t)=3t^3 \,\hat{\mathbf{i}}+2t^2 \,\hat{\mathbf{j}}+\dfrac{1}{t} \,\hat{\mathbf{k}}; \quad t=1$

49)$\vecs r(t)=t \,\hat{\mathbf{i}}+\sin(2t) \,\hat{\mathbf{j}}+\cos(3t) \,\hat{\mathbf{k}}; \quad t=\frac{π}{3}$

Réponse: $\vecs r'\left(\frac{π}{3}\right) = \langle 1, \,-1,0\rangle$est un vecteur tangent, donc un vecteur tangent unitaire serait :
$\frac{1}{\sqrt{2}}⟨1,−1,0⟩ \quad = \quad \langle \frac{\sqrt{2}}{2}, \,-\frac{\sqrt{2}}{2},\, 0\rangle$

50)$\vecs r(t)=\cos(2t) \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}};\quad t=\frac{π}{2}$

51)$\vecs r(t)=3e^t \,\hat{\mathbf{i}}+2e^{−3t} \,\hat{\mathbf{j}}+4e^{2t} \,\hat{\mathbf{k}}; \quad t= \ln(2)$

Réponse: $\vecs r'(\ln(2))= ⟨6,−\frac{3}{4},32⟩$est un vecteur tangent, donc un vecteur tangent unitaire serait :
$\dfrac{1}{\sqrt{1060.5625}}\left\langle 6,−\frac{3}{4},32\right\rangle \quad = \quad \left\langle \dfrac{24\sqrt{16969}}{16969}, -\dfrac{12\sqrt{16969}}{67876}, \frac{128\sqrt{16969}}{16969}\right\rangle$

Pour les questions 52 à 58, trouvez le vecteur de tangente unitaire$\vecs T(t)$ pour les courbes paramétrées suivantes.

52)$\vecs r(t)=t \,\hat{\mathbf{i}}+3t \,\hat{\mathbf{j}}+t^2 \,\hat{\mathbf{k}}$

53)$\vecs r(t)=6 \,\hat{\mathbf{i}}+\cos(3t) \,\hat{\mathbf{j}}+3\sin(4t) \,\hat{\mathbf{k}}, \quad 0≤t<2π$

Réponse: $\vecs T(t)=\dfrac{1}{\sqrt{9\sin ^2 (3t)+144\cos ^2 (4t)}}⟨0,−3\sin(3t),12\cos(4t)⟩$

(54)$\vecs r(t)=⟨t \cos t,t \sin t⟩$

55)$\vecs r(t)=⟨t+1,2t+1,2t+2⟩$

Réponse: $\vecs T(t)=\frac{1}{3} ⟨1,2,2⟩$

56)$\vecs r(t)=\cos t \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}+\sin t \,\hat{\mathbf{k}}, \quad 0≤t<2π$. Deux vues de cette courbe sont présentées ici :

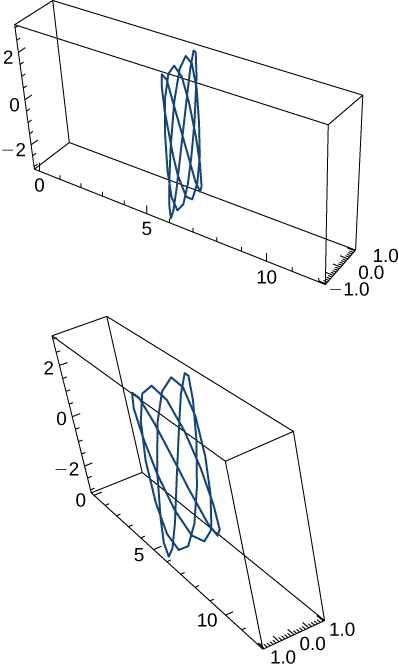
57)$\vecs r(t)=\left\langle t,\dfrac{1}{t}\right\rangle$. Le graphique est présenté ici :

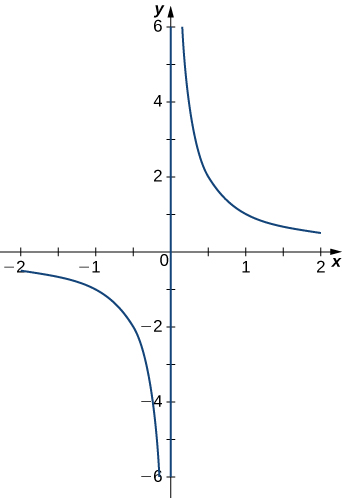
Réponse: $\vecs T(t)=\left\langle\dfrac{t^2}{\sqrt{t^4+1}},\frac{-1}{\sqrt{t^4+1}}\right\rangle$

58)$\vecs r(t)=3 \cos(4t) \,\hat{\mathbf{i}}+3 \sin(4t) \,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}},\quad 1 \le t \le 2$

Réponse: $\vecs T(t)=−\frac{12}{13} \sin(4t) \,\hat{\mathbf{i}}+ \frac{12}{13}\cos (4t) \,\hat{\mathbf{j}}+\frac{5}{13} \,\hat{\mathbf{k}}$

59) Une particule suit la trajectoire d'une hélice avec l'équation$\vecs r(t)= \cos(t) \,\hat{\mathbf{i}}+\sin(t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}$. Voir le graphique présenté ici :

Trouvez ce qui suit :

a. Vitesse de la particule à tout moment

Réponse: $\vecs v(t)=⟨−\sin t,\cos t,1⟩$

b. Vitesse de la particule à tout moment

c. Accélération de la particule à tout moment

Réponse: $\vecs a(t)=−\cos t \,\hat{\mathbf{i}}− \sin t \,\hat{\mathbf{j}}+0 \,\hat{\mathbf{k}}$

d. Déterminez le vecteur tangent unitaire de l'hélice.

Intégration de fonctions à valeur vectorielle

Évaluez les intégrales suivantes :

60)$\displaystyle \int \left(e^t \,\hat{\mathbf{i}}+\sin t \,\hat{\mathbf{j}}+ \frac{1}{2t−1} \,\hat{\mathbf{k}}\right)\, dt$

61)$\displaystyle \int_0^1 \vecs r(t)\,dt$, où$\vecs r(t)=\left\langle\sqrt[3]{t},\dfrac{1}{t+1},e^{−t}\right\rangle$

Réponse: $\frac{3}{4}\,\hat{\mathbf{i}}+\ln(2) \,\hat{\mathbf{j}}+(1−\frac{1}{e}) \,\hat{\mathbf{k}}$

62) Évaluer$\displaystyle \int_0^3‖t\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}‖dt$.

Réponse: $\frac{1}{3}(10^{\frac{3}{2}}−1)$

63) La fonction d'accélération, la vitesse initiale et la position initiale d'une particule sont

\[\begin{align*} \vecs a(t)&=−5 \cos t \,\hat{\mathbf{i}}−5\sin t \,\hat{\mathbf{j}}, \\ \vecs v(0)&=9 \,\hat{\mathbf{i}}+2 \,\hat{\mathbf{j}}, \quad \text{and} \\ \vecs r(0)&=5 \,\hat{\mathbf{i}} \end{align*}\]

Trouvez$\vecs v(t)$ et$\vecs r(t)$.

Réponse: $\vecs v(t) = \left(9 - 5\sin t\right)\,\hat{\mathbf{i}} + \left(-3 + 5\cos t\right)\,\hat{\mathbf{j}}$
$\vecs r(t) = \left(9t + 5\cos t\right)\,\hat{\mathbf{i}} + \left(-3t + 5\sin t\right)\,\hat{\mathbf{j}}$

64) Trouvez l'antidérivé$\vecs r'(t)=\cos(2t) \,\hat{\mathbf{i}}−2\sin t \,\hat{\mathbf{j}}+\dfrac{1}{1+t^2} \,\hat{\mathbf{k}}$ qui satisfait la condition initiale$\vecs r(0)=3 \,\hat{\mathbf{i}}−2 \,\hat{\mathbf{j}}+\,\hat{\mathbf{k}}$.

65) Un objet part de l'arrêt$P(1,2,0)$ et se déplace avec une accélération de$\vecs a(t)=\,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}}$, où elle$‖\vecs a(t)‖$ est mesurée en pieds par seconde et par seconde. Trouvez l'emplacement de l'objet après une$t=2$ seconde.

Contributeurs :

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created questions 11 - 19.