11.4 : Surface et longueur de l'arc en coordonnées polaires

Objectifs d'apprentissage

• Appliquez la formule pour l'aire d'une région en coordonnées polaires.
• Déterminez la longueur de l'arc d'une courbe polaire.

Dans le système de coordonnées rectangulaires, l'intégrale définie permet de calculer l'aire sous une courbe. En particulier, si nous avons une fonction\(y=f(x)\) définie de\(x=a\) à partir de l'\(x=b\)endroit où\(f(x)>0\) sur cet intervalle, l'aire entre la courbe et l'axe des abscisses est donnée par

\[A=\int ^b_af(x)dx. \nonumber \]

Ce fait, ainsi que la formule d'évaluation de cette intégrale, sont résumés dans le théorème fondamental du calcul. De même, la longueur de l'arc de cette courbe est donnée par

\[L=\int ^b_a\sqrt{1+(f′(x))^2}dx. \nonumber \]

Dans cette section, nous étudions des formules analogues pour la surface et la longueur de l'arc dans le système de coordonnées polaires.

Zones de régions délimitées par des courbes polaires

Nous avons étudié les formules de l'aire sous une courbe définie en coordonnées rectangulaires et en courbes définies de manière paramétrique. Nous allons maintenant nous concentrer sur la dérivation d'une formule pour l'aire d'une région délimitée par une courbe polaire. Rappelons que la preuve du théorème fondamental du calcul a utilisé le concept d'une somme de Riemann pour approximer l'aire sous une courbe à l'aide de rectangles. Pour les courbes polaires, nous utilisons à nouveau la somme de Riemann, mais les rectangles sont remplacés par des secteurs de cercle.

Considérons une courbe définie par la fonction\(r=f(θ),\) où\(α≤θ≤β.\) Notre première étape consiste à partitionner l'intervalle\([α,β]\) en n sous-intervalles de largeur égale. La largeur de chaque sous-intervalle est donnée par la formule\(Δθ=(β−α)/n\), et le i ième point de partition\(θ_i\) est donné par la formule\(θ_i=α+iΔθ\). Chaque point de partition\(θ=θ_i\) définit une ligne dont la pente\(\tan θ_i\) passe par le pôle, comme indiqué dans le graphique suivant.

Figure\(\PageIndex{1}\) : Partition d'une courbe typique en coordonnées polaires.

Les segments de ligne sont reliés par des arcs de rayon constant. Cela définit les secteurs dont les surfaces peuvent être calculées à l'aide d'une formule géométrique. La surface de chaque secteur est ensuite utilisée pour approximer la surface entre les segments de ligne successifs. Nous additionnons ensuite les superficies des secteurs pour obtenir une superficie approximative totale. Cette approche donne une approximation de la somme de Riemann pour la superficie totale. La formule pour l'aire d'un secteur de cercle est illustrée dans la figure suivante.

Figure\(\PageIndex{2}\) : L'aire d'un secteur de cercle est donnée par\(A=\dfrac{1}{2}θr^2\).

Rappelez-vous que l'aire d'un cercle est\(A=πr^2\). Lorsque vous mesurez des angles en radians, 360 degrés sont égaux à\(2π\) des radians. Par conséquent, une fraction de cercle peut être mesurée par l'angle central\(θ\). La fraction du cercle est donnée par\(\dfrac{θ}{2π}\), donc la surface du secteur est cette fraction multipliée par la surface totale :

\[A=(\dfrac{θ}{2π})πr^2=\dfrac{1}{2}θr^2. \nonumber \]

Puisque le rayon d'un secteur typique de la figure\(\PageIndex{1}\) est donné par\(r_i=f(θ_i)\), l'aire du secteur i est donnée par

\[A_i=\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Par conséquent, une somme de Riemann qui se rapproche de la surface est donnée par

\[A_n=\sum_{i=1}^nA_i≈\sum_{i=1}^n\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Nous prenons la limite\(n→∞\) pour obtenir la superficie exacte :

\[A=\lim_{n→∞}A_n=\dfrac{1}{2}\int ^β_α(f(θ))^2dθ. \nonumber \]

Cela donne le théorème suivant.

Aire d'une région délimitée par une courbe polaire

Supposons que\(f\) c'est continu et non négatif sur l'intervalle\(α≤θ≤β\) avec\(0<β−α≤2π\). L'aire de la région délimitée par le graphe\(r=f(θ)\) entre les lignes radiales\(θ=α\) et\(θ=β\) est

\[\begin{align} A =\dfrac{1}{2}\int ^β_α[f(θ)]^2 dθ \\[4pt] =\dfrac{1}{2}\int ^β_αr^2 dθ. \label{areapolar}\end{align} \]

Exemple\(\PageIndex{1}\): Finding an Area of a Polar Region

Détermine l'aire d'un pétale de rose définie par l'équation\(r=3\sin(2θ).\)

Solution

Le graphique\(r=3\sin (2θ)\) suivant.

Figure\(\PageIndex{3}\) : Le graphique de\(r=3\sin (2θ).\)

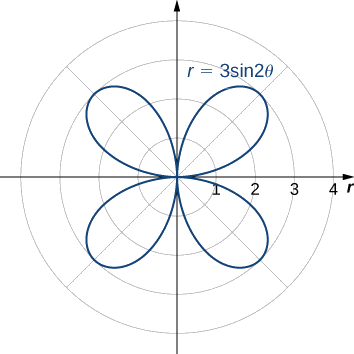
Quand\(θ=0\) nous l'aurons fait\(r=3\sin(2(0))=0\). La valeur suivante pour laquelle\(r=0\) est\(θ=π/2\). Cela peut être vu en résolvant l'équation\(3\sin (2θ)=0\) pour\(θ\). D'où les valeurs\(θ=0\) permettant de\(θ=π/2\) tracer le premier pétale de la rose. Pour trouver la zone située à l'intérieur de ce pétale, utilisez l'équation \ ref {areapolar} avec\(f(θ)=3\sin (2θ), α=0,\) et\(β=π/2\) :

\[\begin{align*} A &=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_0[3\sin (2θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ. \end{align*}\]

Pour évaluer cette intégrale, utilisez la formule\(\sin^2α=(1−\cos (2α))/2\) avec\(α=2θ:\)

\[\begin{align*} A &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ \\[4pt] &=\dfrac{9}{2}\int ^{π/2}_0\dfrac{(1−\cos(4θ))}{2}dθ \\[4pt] &=\dfrac{9}{4}(\int ^{π/2}_01−\cos(4θ)dθ) \\[4pt] &=\dfrac{9}{4}(θ−\dfrac{\sin(4θ)}{4}∣^{π/2}_0 \\[4pt] &=\dfrac{9}{4}(\dfrac{π}{2}−\dfrac{\sin 2π}{4})−\dfrac{9}{4}(0−\dfrac{\sin 4(0)}{4}) \\[4pt] &=\dfrac{9π}{8}\end{align*}\]

Exercice\(\PageIndex{1}\)

Déterminez la zone à l'intérieur de la cardioïde définie par l'équation\(r=1−\cos θ\).

Allusion

Utilisez l'équation \ ref {areapolar}. Assurez-vous de déterminer les bonnes limites d'intégration avant de procéder à une évaluation.

Réponse

\(A=3π/2\)

L'exemple\(\PageIndex{1}\) consistait à trouver l'aire à l'intérieur d'une courbe. Nous pouvons également utiliser l'équation \ ref {areapolar} pour trouver l'aire entre deux courbes polaires. Cependant, nous avons souvent besoin de trouver les points d'intersection des courbes et de déterminer quelle fonction définit la courbe extérieure ou la courbe intérieure entre ces deux points.

Exemple\(\PageIndex{2}\): Finding the Area between Two Polar Curves

Trouvez la zone à l'extérieur du cardioïde\(r=2+2\sin θ\) et à l'intérieur du cercle\(r=6\sin θ\).

Solution

Dessinez d'abord un graphique contenant les deux courbes, comme indiqué.

Figure\(\PageIndex{4}\) : La région située entre les courbes\(r=2+2\sin θ\) et\(r=6\sin θ.\)

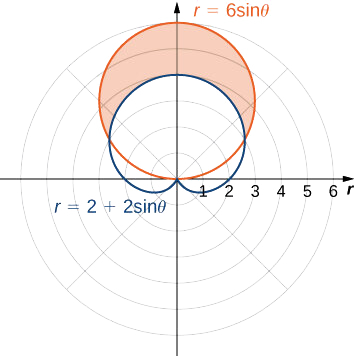
Pour déterminer les limites de l'intégration, trouvez d'abord les points d'intersection en mettant les deux fonctions égales l'une à l'autre et en résolvant les problèmes\(θ\) suivants :

\[\begin{align*} 6 \sin θ &=2+2\sin θ \\[4pt] 4\sin θ &=2 \\[4pt] \sin θ &=\dfrac{1}{2} \end{align*}. \nonumber \]

Cela donne les solutions\(θ=\dfrac{π}{6}\) et\(θ=\dfrac{5π}{6}\), qui sont les limites de l'intégration. Le cercle\(r=3\sin θ\) est le graphe rouge, qui est la fonction externe, et le cardioïde\(r=2+2\sin θ\) est le graphe bleu, qui est la fonction interne. Pour calculer l'aire entre les courbes, commencez par la zone située à l'intérieur du cercle entre\(θ=\dfrac{π}{6}\) et\(θ=\dfrac{5π}{6}\), puis soustrayez la zone située à l'intérieur de la cardioïde entre\(θ=\dfrac{π}{6}\) et\(θ=\dfrac{5π}{6}\) :

\(A=\text{circle}−\text{cardioid}\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}[6\sin θ]^2dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}[2+2\sin θ]^2dθ\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}36\sin^2θ\,dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}4+8\sin θ+4\sin^2θ\,dθ\)

\(=18\int ^{5π/6}_{π/6}\dfrac{1−\cos(2θ)}{2}dθ−2\int ^{5π/6}_{π/6}1+2\sin θ+\dfrac{1−\cos(2θ)}{2}dθ\)

\(=9[θ−\dfrac{\sin(2θ)}{2}]^{5π/6}_{π/6}−2[\dfrac{3θ}{2}−2\cos θ−\dfrac{\sin(2θ)}{4}]^{5π/6}_{π/6}\)

\(=9(\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})−9(\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})−(3(\dfrac{5π}{6})−4\cos\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})+(3(\dfrac{π}{6})−4\cos\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})\)

\(=4π\).

Exercice\(\PageIndex{2}\)

Trouvez la zone à l'intérieur du cercle\(r=4\cos θ\) et à l'extérieur du cercle\(r=2\).

Allusion

Utilisez l'équation \ ref {areapolar} et tirez parti de la symétrie.

Réponse

\(A=\dfrac{4π}{3}+2\sqrt{3}\)

Dans l'exemple,\(\PageIndex{2}\) nous avons trouvé la zone à l'intérieur du cercle et à l'extérieur du cardioïde en trouvant d'abord leurs points d'intersection. Notez que la résolution directe de l'équation pour\(θ\) a donné deux solutions :\(θ=\dfrac{π}{6}\) et\(θ=\dfrac{5π}{6}\). Cependant, dans le graphique, il y a trois points d'intersection. Le troisième point d'intersection est l'origine. La raison pour laquelle ce point n'apparaissait pas comme solution est que l'origine se trouve sur les deux graphes mais pour des valeurs différentes de\(θ\). Par exemple, pour le cardioïde, nous obtenons

\[\begin{align*} 2+2\sin θ =0 \\[4pt] \sin θ =−1 ,\end{align*}. \nonumber \]

donc les valeurs pour\(θ\) qui résolvent cette équation sont\(θ=\dfrac{3π}{2}+2nπ\), où\(n\) est un entier. Pour le cercle, nous obtenons

\[6\sin θ=0. \nonumber \]

Les solutions de cette équation sont de la forme\(θ=nπ\) pour toute valeur entière de\(n\). Ces deux ensembles de solutions n'ont aucun point commun. Indépendamment de ce fait, les courbes se croisent à l'origine. Ce cas doit toujours être pris en considération.

Longueur de l'arc dans les courbes polaires

Nous dérivons ici une formule pour la longueur de l'arc d'une courbe définie en coordonnées polaires. En coordonnées rectangulaires, la longueur de l'arc d'une courbe paramétrée\((x(t),y(t))\) pour\(a≤t≤b\) est donnée par

\[L=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt. \nonumber \]

En coordonnées polaires, nous définissons la courbe par l'équation\(r=f(θ)\), où\(α≤θ≤β.\) Pour adapter la formule de longueur d'arc pour une courbe polaire, nous utilisons les équations

\[x=r\cos θ=f(θ)\cos θ \nonumber \]

et

\[y=r\sin θ=f(θ)\sin θ, \nonumber \]

et nous remplaçons le paramètre\(t\) par\(θ\). Alors

\[\dfrac{dx}{dθ}=f′(θ)\cos θ−f(θ)\sin θ \nonumber \]

\[\dfrac{dy}{dθ}=f′(θ)\sin θ+f(θ)\cos θ. \nonumber \]

Nous les remplaçons\(dt\) par\(dθ\), et les limites inférieure et supérieure de l'intégration sont\(α\) et\(β\), respectivement. Ensuite, la formule de longueur d'arc devient

\[ \begin{align*} L &=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \\[4pt] &=\int ^β_α\sqrt{\left(\dfrac{dx}{dθ}\right)^2+\left(\dfrac{dy}{dθ}\right)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ)\cos θ−f(θ)\sin θ)^2+(f′(θ)\sin θ+f(θ)\cos θ)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2(\cos^2 θ+\sin^2 θ)+(f(θ))^2(\cos^2 θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2+(f(θ))^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ \end{align*}\]

Cela nous donne le théorème suivant.

Longueur d'arc d'une courbe définie par une fonction polaire

\(f\)Soit une fonction dont la dérivée est continue sur un intervalle\(α≤θ≤β\). La longueur du graphique\(r=f(θ)\) de\(θ=α\) à\(θ=β\) est

\[ \begin{align} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \label{arcpolar1} \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ. \label{arcpolar2} \end{align} \]

Exemple\(\PageIndex{3}\): Finding the Arc Length of a cardioid

Détermine la longueur de l'arc du cardioïde\(r=2+2\cos θ\).

Solution

Quand en\(θ=0,r=2+2\cos 0 =4.\) outre, comme\(θ\) cela va de\(0\) à\(2π\), le cardioïde est tracé exactement une fois. Telles sont donc les limites de l'intégration. L'utilisation\(f(θ)=2+2\cos θ, α=0,\) de\(β=2π,\) l'équation \ ref {arcpolar1} devient

\[\begin{align*} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{[2+2\cos θ]^2+[−2\sin θ]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4\cos^2θ+4\sin^2θ}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4(\cos^2θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{8+8\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ. \end{align*}\]

Ensuite, en utilisant l'identité,\(\cos(2α)=2\cos^2α−1,\) ajoutez 1 aux deux côtés et multipliez par 2. Cela donne la\(2+2\cos(2α)=4\cos^2α.\) substitution\(α=θ/2\) donne\(2+2\cos θ=4\cos^2(θ/2)\), de sorte que l'intégrale devient

\[\begin{align*} L &= 2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{4\cos^2(\dfrac{θ}{2})}\,dθ \\[4pt] &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ.\end{align*}\]

La valeur absolue est nécessaire car le cosinus est négatif pour certaines valeurs de son domaine. Pour résoudre ce problème, modifiez les limites de\(0\) à\(π\) et doublez la réponse. Cette stratégie fonctionne car le cosinus est positif entre\(0\) et\(\dfrac{π}{2}\). Ainsi,

\[\begin{align*} L &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ \\[4pt] &=8\int ^π_0 \cos(\dfrac{θ}{2})\,dθ \\[4pt] &=8(2\sin(\dfrac{θ}{2})∣^π_0 \\[4pt] &=16\end{align*}\]

Exercice\(\PageIndex{3}\)

Détermine la longueur totale de l'arc de\(r=3\sin θ\).

Allusion

Utilisez l'équation \ ref {arcpolar1}. Pour déterminer les limites correctes, créez un tableau de valeurs.

Réponse

\(s=3π\)

Concepts clés

• L'aire d'une région en coordonnées polaires définie par l'équation\(r=f(θ)\) avec\(α≤θ≤β\) est donnée par l'intégrale\(A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\).
• Pour déterminer l'aire entre deux courbes dans le système de coordonnées polaires, trouvez d'abord les points d'intersection, puis soustrayez les zones correspondantes.
• La longueur de l'arc d'une courbe polaire définie par l'équation\(r=f(θ)\) avec\(α≤θ≤β\) est donnée par l'intégrale\(L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ\).

Équations clés

• Aire d'une région délimitée par une courbe polaire\[A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ=\dfrac{1}{2}\int ^β_αr^2dθ \nonumber \]
• Longueur de l'arc d'une courbe polaire\[L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ \nonumber \]