8.4 : L'équation logistique

Last updated
Save as PDF

Page ID: 197413

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Décrire le concept de capacité de charge environnementale dans le modèle logistique de la croissance démographique.
Dessinez un champ de direction pour une équation logistique et interprétez les courbes de solution.
Résolvez une équation logistique et interprétez les résultats.

Des équations différentielles peuvent être utilisées pour représenter la taille d'une population telle qu'elle varie dans le temps. Nous l'avons vu dans un chapitre précédent de la section sur la croissance et la décroissance exponentielles, qui est le modèle le plus simple. Un modèle plus réaliste inclut d'autres facteurs qui influent sur la croissance de la population. Dans cette section, nous étudions l'équation différentielle logistique et voyons comment elle s'applique à l'étude de la dynamique des populations dans le contexte de la biologie.

Croissance démographique et capacité d'accueil

Pour modéliser la croissance démographique à l'aide d'une équation différentielle, nous devons d'abord introduire certaines variables et certains termes pertinents. La variable$t$. représentera le temps. Les unités de temps peuvent être des heures, des jours, des semaines, des mois ou même des années. Tout problème donné doit spécifier les unités utilisées dans ce problème particulier. La variable$P$ représentera la population. Comme la population varie au fil du temps, elle est considérée comme une fonction du temps. Nous utilisons donc la notation$P(t)$ de la population en fonction du temps. S'il s'$P(t)$agit d'une fonction dérivable, alors la dérivée première$\frac{dP}{dt}$ représente le taux instantané de variation de la population en fonction du temps.

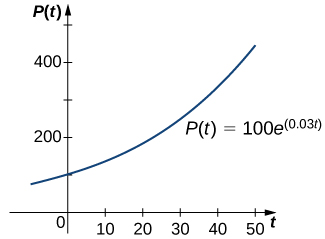
Dans Croissance et décroissance exponentielles, nous avons étudié la croissance et la décroissance exponentielles des populations et des substances radioactives. Un exemple de fonction de croissance exponentielle est$P(t)=P_0e^{rt}.$ Dans cette fonction,$P(t)$ représente la population à la fois,$t,P_0$ représente la population initiale (population à l'époque$t=0$), et la constante$r>0$ est appelée taux de croissance. La figure$\PageIndex{1}$ montre un graphique de$P(t)=100e^{0.03t}$. Ici$P_0=100$ et$r=0.03$.

Un graphique d'une fonction exponentielle p (t) = 100 e ^ (0,03 t). Il s'agit d'une fonction ascendante concave croissante qui commence dans le quadrant 2, traverse l'axe y en (0, 100) et augmente dans le quadrant 1. — Figure$\PageIndex{1}$ : Un modèle de croissance exponentielle de la population.

Nous pouvons vérifier que la fonction$P(t)=P_0e^{rt}$ répond au problème de valeur initiale

\[ \dfrac{dP}{dt}=rP \nonumber \]

avec$P(0)=P_0.$

L'interprétation de cette équation différentielle est intéressante. Le côté gauche représente le taux auquel la population augmente (ou diminue). Le côté droit est égal à une constante positive multipliée par la population actuelle. Par conséquent, l'équation différentielle indique que le taux auquel la population augmente est proportionnel à la population à ce moment-là. En outre, il indique que la constante de proportionnalité ne change jamais.

L'un des problèmes de cette fonction est qu'elle prédit qu'au fil du temps, la population croît sans limite. Cela n'est pas réaliste dans un contexte réel. Divers facteurs limitent le taux de croissance d'une population donnée, notamment le taux de natalité, le taux de mortalité, l'approvisionnement alimentaire, les prédateurs, etc. La constante de croissance prend$r$ généralement en compte les taux de natalité et de mortalité, mais aucun autre facteur, et elle peut être interprétée comme un taux de croissance net (naissance moins décès) par unité de temps. Il est naturel de se demander si le taux de croissance de la population reste constant ou s'il évolue au fil du temps. Les biologistes ont découvert que dans de nombreux systèmes biologiques, la population augmente jusqu'à atteindre un certain état d'équilibre. Cette possibilité n'est pas prise en compte dans le cas d'une croissance exponentielle. Cependant, le concept de capacité de charge permet la possibilité que, dans une zone donnée, seul un certain nombre d'organismes ou d'animaux puissent prospérer sans rencontrer de problèmes de ressources.

Définition : Capacité de charge

La capacité de charge d'un organisme dans un environnement donné est définie comme étant la population maximale de cet organisme que l'environnement peut maintenir indéfiniment.

Nous utilisons la variable$K$ pour indiquer la capacité de charge. Le taux de croissance est représenté par la variable$r$. À l'aide de ces variables, nous pouvons définir l'équation différentielle logistique.

Définition : Équation différentielle logistique

Soit$K$ la capacité de charge d'un organisme particulier dans un environnement donné, et$r$ soit un nombre réel qui représente le taux de croissance. La fonction$P(t)$ représente la population de cet organisme en fonction du temps$t$, et la constante$P_0$ représente la population initiale (population de l'organisme au temps$t=0$). L'équation différentielle logistique est alors

\[\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right). \label{LogisticDiffEq} \]

L'équation logistique a été publiée pour la première fois par Pierre Verhulst dans$1845$. Cette équation différentielle peut être couplée à la condition initiale$P(0)=P_0$ pour former un problème de valeur initiale pour$P(t).$

Supposons que la population initiale soit faible par rapport à la capacité de charge. Alors$\frac{P}{K}$ est petit, peut-être proche de zéro. Ainsi, la quantité entre parenthèses sur le côté droit de l'équation \ ref {LogisticDiffeq} est proche de$1$, et la partie droite de cette équation est proche de$rP$. Si$r>0$, alors la population augmente rapidement, ressemblant à une croissance exponentielle.

Cependant, à mesure que la population augmente, le ratio augmente$\frac{P}{K}$ également, car$K$ il est constant. Si la population reste inférieure à la capacité de charge, alors$\frac{P}{K}$ est inférieure à$1$, donc$1−\frac{P}{K}>0$. Par conséquent, le côté droit de l'équation \ ref {LogisticDiffEq} est toujours positif, mais la quantité entre parenthèses diminue et le taux de croissance diminue en conséquence. Si$P=K$ alors le côté droit est égal à zéro et que la population ne change pas.

Supposons maintenant que la population commence à une valeur supérieure à la capacité de charge. Puis$\frac{P}{K}>1,$ et$1−\frac{P}{K}<0$. Ensuite, le côté droit de l'équation \ ref {LogisticDiffEq} est négatif et la population diminue. Tant que$P>K$ la population diminue. Elle n'atteint jamais K car elle$\frac{dP}{dt}$ deviendra de plus en plus petite, mais la population s'approche de la capacité de charge à mesure que l'infini se$t$ rapproche de l'infini. Cette analyse peut être représentée visuellement au moyen d'une ligne de phase. Une ligne de phase décrit le comportement général d'une solution à une équation différentielle autonome, en fonction de la condition initiale. Pour le cas d'une capacité de charge dans l'équation logistique, la ligne de phase est celle indiquée sur la figure$\PageIndex{2}$.

Diagramme de la ligne de phase pour l'équation différentielle donnée. Une ligne bleue verticale avec des flèches à chaque extrémité comporte deux points marqués, à P = K et P = 0, par K — Figure$\PageIndex{2}$ : Une ligne de phase pour l'équation différentielle$\dfrac{dP}{dt}=rP(1−\dfrac{P}{K}).$

Cette ligne de phase montre que lorsque la valeur$P$ est inférieure à zéro ou supérieure à zéro$K$, la population diminue avec le temps. Quand$P$ se situe entre$0$ et$K$, la population augmente avec le temps.

Exemple$\PageIndex{1}$: Examining the Carrying Capacity of a Deer Population

Prenons la population de cerfs de Virginie (Odocoileus virginianus) dans l'État du Kentucky. Le ministère des Ressources halieutiques et fauniques du Kentucky (KDFWR) établit des directives pour la chasse et la pêche dans l'État. Avant la saison de chasse de 2004, la population était estimée à 900 000 cerfs. Johnson note : « Une population de cerfs qui ont beaucoup à manger et qui n'est pas chassée par les humains ou d'autres prédateurs doublera tous les trois ans. » (George Johnson, « The Problem of Exploding Deer Populations Has No Attractive Solutions », 12 janvier 2001, consulté le 9 avril 2015)

Voici la photographie d'un cerf. — Figure$\PageIndex{3}$ : (source : modification de l'œuvre de Rachel Kramer, Flickr)

Cette observation correspond à un taux d'augmentation, de$r=\dfrac{\ln (2)}{3}=0.2311,$ sorte que le taux de croissance approximatif est de 23,11 % par an. (Cela suppose que la population croît de façon exponentielle, ce qui est raisonnable, du moins à court terme, avec une alimentation abondante et l'absence de prédateurs.) Le KDFWR rapporte également les densités de population de cerfs dans 32 comtés du Kentucky, dont la moyenne est d'environ 27 cerfs par mile carré. Supposons qu'il s'agisse de la densité des cerfs pour l'ensemble de l'État (39 732 miles carrés). La capacité de charge$K$ est de 39 732 miles carrés fois 27 cerfs par mile carré, soit 1 072 764 cerfs.

Pour cette application, nous avons$P_0=900,000,K=1,072,764,$ et$r=0.2311.$ substituons ces valeurs dans l'équation \ ref {LogisticDiffeq} et formons le problème de valeur initiale.
Résolvez le problème de la valeur initiale à partir de la partie a.
Selon ce modèle, quelle sera la population dans les$3$ années à venir ? Rappelons que le temps de doublement prédit par Johnson pour la population de cerfs était de$3$ plusieurs années. Comment se comparent ces valeurs ?

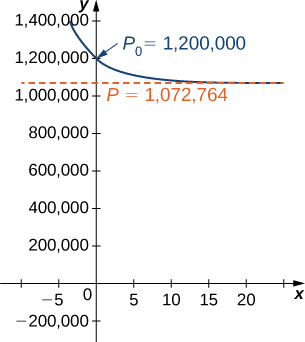
Supposons que la population ait réussi à atteindre 1 200 000 habitants. Que prévoit l'équation logistique pour la population dans ce scénario ?

Solution

a. Le problème de valeur initiale est

\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right),\,\,P(0)=900,000. \nonumber \]

b. L'équation logistique est une équation différentielle autonome, nous pouvons donc utiliser la méthode de séparation des variables.

Étape 1 : Mettre le côté droit à zéro donne$P=0$ et$P=1,072,764.$ Cela signifie que si la population commence à zéro, elle ne changera jamais, et si elle commence à la capacité de charge, elle ne changera jamais.

Étape 2 : Réécrivez l'équation différentielle et multipliez les deux côtés par :

\[ \begin{align*} \dfrac{dP}{dt} =0.2311P\left(\dfrac{1,072,764−P}{1,072,764} \right) \\[4pt] dP =0.2311P\left(\dfrac{1,072,764−P}{1,072,764}\right)dt \\[4pt] \dfrac{dP}{P(1,072,764−P)} =\dfrac{0.2311}{1,072,764}dt. \end{align*}\]

Étape 3 : Intégrez les deux côtés de l'équation à l'aide de la décomposition par fractions partielles :

\[ \begin{align*} ∫\dfrac{dP}{P(1,072,764−P)} =∫\dfrac{0.2311}{1,072,764}dt \\[4pt] \dfrac{1}{1,072,764}∫ \left(\dfrac{1}{P}+\dfrac{1}{1,072,764−P}\right)dP =\dfrac{0.2311t}{1,072,764}+C \\[4pt] \dfrac{1}{1,072,764}\left(\ln |P|−\ln |1,072,764−P|\right) =\dfrac{0.2311t}{1,072,764}+C. \end{align*} \nonumber \]

Étape 4 : Multipliez les deux côtés par 1 072 764 et utilisez la règle du quotient pour les logarithmes :

\[\ln \left|\dfrac{P}{1,072,764−P}\right|=0.2311t+C_1. \nonumber \]

Ici$C_1=1,072,764C.$, exponentiez les deux côtés et éliminez la valeur absolue :

\[ \begin{align*} e^{\ln \left|\dfrac{P}{1,072,764−P} \right|} =e^{0.2311t + C_1} \\[4pt] \left|\dfrac{P}{1,072,764 - P}\right| =C_2e^{0.2311t} \\[4pt] \dfrac{P}{1,072,764−P} =C_2e^{0.2311t}. \end{align*}\]

Ici$C_2=e^{C_1}$, mais après élimination de la valeur absolue, elle peut également être négative. Résolvez maintenant pour :

\[ \begin{align*} P =C_2e^{0.2311t}(1,072,764−P) \\[4pt] P =1,072,764C_2e^{0.2311t}−C_2Pe^{0.2311t} \\[4pt] P + C_2Pe^{0.2311t} = 1,072,764C_2e^{0.2311t} \\[4pt] P(1+C_2e^{0.2311t} =1,072,764C_2e^{0.2311t} \\[4pt] P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.23\nonumber11t}}. \end{align*}\]

Étape 5 : Pour déterminer la valeur de$C_2$, il est en fait plus facile de revenir en arrière quelques étapes jusqu'à l'endroit où elle$C_2$ a été définie. En particulier, utilisez l'équation

\[\dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]

La condition initiale est$P(0)=900,000$. Remplacer$P$ par$900,000$ et$t$ par zéro :

\[ \begin{align*} \dfrac{P}{1,072,764−P} =C_2e^{0.2311t} \\[4pt] \dfrac{900,000}{1,072,764−900,000} =C_2e^{0.2311(0)} \\[4pt] \dfrac{900,000}{172,764} =C_2 \\[4pt] C_2 =\dfrac{25,000}{4,799} \\[4pt] ≈5.209. \end{align*}\]

Donc

\[ \begin{align*} P(t) =\dfrac{1,072,764 \left(\dfrac{25000}{4799}\right)e^{0.2311t}}{1+(250004799)e^{0.2311t}}\\[4pt] =\dfrac{1,072,764(25000)e^{0.2311t}}{4799+25000e^{0.2311t}.} \end{align*}\]

Diviser le numérateur et le dénominateur par 25 000 donne

\[P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]

La figure est un graphique de cette équation.

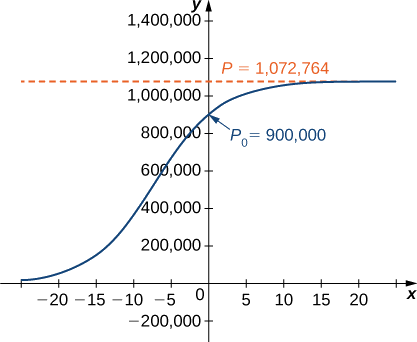
Un graphique d'une courbe logistique pour la population de cerfs avec une population initiale P_0 de 900 000. Le graphique commence par une fonction ascendante concave croissante dans le quadrant deux, passe à une fonction concave descendante croissante, traverse l'axe x à (0, 900 000) et se rapproche de manière asymptotique de P = 1 072 764 lorsque x passe à l'infini. — Figure$\PageIndex{4}$ : Courbe logistique de la population de cerfs avec une population initiale de **900 000** cerfs.

c. À l'aide de ce modèle, nous pouvons prédire la population dans 3 ans.

\[P(3)=\dfrac{1,072,764e^{0.2311(3)}}{0.19196+e^{0.2311(3)}}≈978,830\,deer \nonumber \]

C'est bien moins du double de la population initiale de$900,000.$ Souvenez-vous que le temps de doublement est basé sur l'hypothèse que le taux de croissance ne change jamais, mais le modèle logistique tient compte de cette possibilité.

d. Si la population atteignait 1 200 000 cerfs, le nouveau problème de valeur initiale serait

\[ \dfrac{dP}{dt}=0.2311P \left(1−\dfrac{P}{1,072,764}\right), \, P(0)=1,200,000. \nonumber \]

La solution générale de l'équation différentielle resterait la même.

\[ P(t)=\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \nonumber \]

Pour déterminer la valeur de la constante, retournez à l'équation

\[ \dfrac{P}{1,072,764−P}=C_2e^{0.2311t}. \nonumber \]

En remplaçant les valeurs$t=0$,$P=1,200,000,$ vous obtenez

\[ \begin{align*} C_2e^{0.2311(0)} =\dfrac{1,200,000}{1,072,764−1,200,000} \\[4pt] C_2 =−\dfrac{100,000}{10,603}≈−9.431.\end{align*}\]

Donc

\[ \begin{align*} P(t) =\dfrac{1,072,764C_2e^{0.2311t}}{1+C_2e^{0.2311t}} \\[4pt] =\dfrac{1,072,764 \left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}}{1+\left(−\dfrac{100,000}{10,603}\right)e^{0.2311t}} \\[4pt] =−\dfrac{107,276,400,000e^{0.2311t}}{100,000e^{0.2311t}−10,603} \\[4pt] ≈\dfrac{10,117,551e^{0.2311t}}{9.43129e^{0.2311t}−1} \end{align*}\]

Cette équation est représentée graphiquement dans la figure$\PageIndex{5}$.

Un graphique de la courbe logistique pour une population initiale de 1 200 000 cerfs. Le graphique est une fonction ascendante concave décroissante qui commence dans le quadrant deux, traverse l'axe y à (0, 1 200 000) et s'approche asymptotiquement de P = 1 072 764 lorsque x passe à l'infini. — Figure$\PageIndex{5}$ : Courbe logistique de la population de cerfs avec une population initiale de **1 200 000** cerfs.

Résolution de l'équation différentielle logistique

L'équation différentielle logistique est une équation différentielle autonome, nous pouvons donc utiliser la séparation des variables pour trouver la solution générale, comme nous venons de le faire dans Example$\PageIndex{1}$.

Étape 1 : Mettre le côté droit à zéro conduit à$P=0$ et en$P=K$ tant que solutions constantes. La première solution indique que lorsqu'aucun organisme n'est présent, la population n'augmentera jamais. La deuxième solution indique que lorsque la population commence à atteindre sa capacité de charge, elle ne changera jamais.

Étape 2 : Réécrire l'équation différentielle dans le formulaire

\[ \dfrac{dP}{dt}=\dfrac{rP(K−P)}{K}. \nonumber \]

Multipliez ensuite les deux côtés par$dt$ et divisez les deux côtés par$P(K−P).$ Cela conduit à

\[ \dfrac{dP}{P(K−P)}=\dfrac{r}{K}dt. \nonumber \]

Multipliez les deux côtés de l'équation par$K$ et intégrez :

\[ ∫\dfrac{K}{P(K−P)}dP=∫rdt. \label{eq20a} \]

Le côté gauche de cette équation peut être intégré à l'aide d'une décomposition par fraction partielle. Nous vous laissons le soin de vérifier que

\[ \dfrac{K}{P(K−P)}=\dfrac{1}{P}+\dfrac{1}{K−P}. \nonumber \]

Ensuite, l'équation \ ref {eq20a} devient

\[ ∫\dfrac{1}{P}+\dfrac{1}{K−P}dP=∫rdt \nonumber \]

\[ \ln |P|−\ln |K−P|=rt+C \nonumber \]

\[ \ln ∣\dfrac{P}{K−P}∣=rt+C. \nonumber \]

Maintenant, exponentiez les deux côtés de l'équation pour éliminer le logarithme naturel :

\[ e^{\ln ∣\dfrac{P}{K−P}∣}=e^{rt+C} \nonumber \]

\[ ∣\dfrac{P}{K−P}∣=e^Ce^{rt}. \nonumber \]

Nous définissons de$C_1=e^c$ telle sorte que l'équation devienne

\[ \dfrac{P}{K−P}=C_1e^{rt}. \label{eq30a} \]

Pour résoudre cette équation$P(t)$, multipliez d'abord les deux côtés par$K−P$ et collectez$P$ les termes contenus dans la partie gauche de l'équation :

\[\begin{align*} P =C_1e^{rt}(K−P) \\[4pt] =C_1Ke^{rt}−C_1Pe^{rt} \\[4pt] P+C_1Pe^{rt} =C_1Ke^{rt}.\end{align*}\]

Ensuite, factorisez$P$ à partir du côté gauche et divisez les deux côtés par l'autre facteur :

\[\begin{align*} P(1+C_1e^{rt}) =C_1Ke^{rt} \\[4pt] P(t) =\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}. \end{align*}\]

La dernière étape consiste à déterminer la valeur de.$C_1.$ Le moyen le plus simple de le faire est de remplacer$t=0$ et de remplacer$P_0$$P$ dans l'équation et de résoudre par$C_1$ :

\[\begin{align*} \dfrac{P}{K−P} = C_1e^{rt} \\[4pt] \dfrac{P_0}{K−P_0} =C_1e^{r(0)} \\[4pt] C_1 = \dfrac{P_0}{K−P_0}. \end{align*}\]

Enfin, remplacez l'expression par$C_1$ dans l'équation \ ref {eq30a} :

\[ P(t)=\dfrac{C_1Ke^{rt}}{1+C_1e^{rt}}=\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \nonumber \]

Multipliez maintenant le numérateur et le dénominateur du côté droit par$(K−P_0)$ et simplifiez :

\[\begin{align*} P(t) =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}} \\[4pt] =\dfrac{\dfrac{P_0}{K−P_0}Ke^{rt}}{1+\dfrac{P_0}{K−P_0}e^{rt}}⋅\dfrac{K−P_0}{K−P_0} =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}. \end{align*}\]

Nous énonçons ce résultat sous forme de théorème.

Solution de l'équation différentielle logistique

Considérez l'équation différentielle logistique soumise à une population initiale$P_0$ ayant une capacité de charge$K$ et un taux de croissance$r$. La solution au problème de valeur initiale correspondant est donnée par

\[P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \nonumber \].

Maintenant que nous avons trouvé la solution au problème de la valeur initiale, nous pouvons choisir des valeurs pour$P_0,r$$K$ et étudier la courbe de solution. Par exemple, dans Example, nous avons utilisé les valeurs$r=0.2311,K=1,072,764,$ et une population initiale de$900,000$ cerfs. Cela conduit à la solution

\[\begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{(1,072,764−900,000)+900,000e^{0.2311t}}\\[4pt] =\dfrac{900,000(1,072,764)e^{0.2311t}}{172,764+900,000e^{0.2311t}}.\end{align*}\]

Diviser le haut et le bas par$900,000$ donne

\[ P(t)=\dfrac{1,072,764e^{0.2311t}}{0.19196+e^{0.2311t}}. \nonumber \]

Il s'agit de la même solution que celle d'origine. Le graphique de cette solution est à nouveau représenté en bleu sur la figure$\PageIndex{6}$, superposé au graphique du modèle de croissance exponentielle avec population$900,000$ et taux de croissance initiaux$0.2311$ (apparaissant en vert). La ligne pointillée rouge représente la capacité de charge et constitue une asymptote horizontale pour la solution de l'équation logistique.

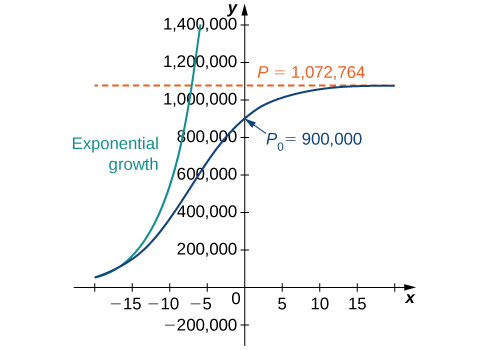
Un graphique montrant une croissance exponentielle et logistique pour la même population initiale de 900 000 organismes et un taux de croissance de 23,11 %. Les deux commencent dans le quadrant deux, près de l'axe x, sous forme de courbes ascendantes concaves croissantes. La courbe de croissance exponentielle continue de croître, passant P = 1 072 764 alors qu'elle se trouve toujours dans le deuxième quadrant. La courbe de croissance logistique change de concavité, traverse l'axe x à P_0 = 900 000 et s'approche asymptotiquement de P = 1 072 764. — Figure$\PageIndex{6}$ : Comparaison de la croissance exponentielle par rapport à la croissance logistique pour la même population initiale d'$900,000$organismes et le même taux de croissance de$23.11%.$

En partant de l'hypothèse que la population croît selon l'équation différentielle logistique, ce graphique prédit qu'environ des$20$ années plus tôt$(1984)$, la croissance de la population était presque exponentielle. Le taux de croissance net à cette époque aurait été d'$23.1%$environ chaque année. Au fil du temps, les deux graphes se séparent. Cela se produit parce que la population augmente et que l'équation différentielle logistique indique que le taux de croissance diminue à mesure que la population augmente. Au moment où la population a été mesurée$(2004)$, elle était proche de sa capacité de charge et la population commençait à se stabiliser.

La solution de l'équation différentielle logistique possède un point d'inflexion. Pour trouver ce point, définissez la dérivée seconde égale à zéro :

\[ \begin{align*} P(t) =\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}} \\[4pt] P′(t) =\dfrac{rP_0K(K−P0)e^{rt}}{((K−P_0)+P_0e^{rt})^2} \\[4pt] P''(t) =\dfrac{r^2P_0K(K−P_0)^2e^{rt}−r^2P_0^2K(K−P_0)e^{2rt}}{((K−P_0)+P_0e^{rt})^3} \\[4pt] =\dfrac{r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})}{((K−P_0)+P_0e^{rt})^3}. \end{align*}\]

Mettre le numérateur à zéro,

\[ r^2P_0K(K−P_0)e^{rt}((K−P_0)−P_0e^{rt})=0. \nonumber \]

Tant que$P_0≠K$ la quantité totale avant et inclus$e^{rt}$ est différente de zéro, nous pouvons donc la diviser :

\[ (K−P_0)−P_0e^{rt}=0. \nonumber \]

Résoudre pour$t$,

\[ P_0e^{rt}=K−P_0 \nonumber \]

\[ e^{rt}=\dfrac{K−P_0}{P_0} \nonumber \]

\[ \ln e^{rt}=\ln \dfrac{K−P_0}{P_0} \nonumber \]

\[ rt=\ln \dfrac{K−P_0}{P_0} \nonumber \]

\[ t=\dfrac{1}{r}\ln \dfrac{K−P_0}{P_0}. \nonumber \]

Notez que si$P_0>K$, alors cette quantité n'est pas définie et le graphique n'a pas de point d'inflexion. Dans le graphe logistique, le point d'inflexion peut être considéré comme le point où le graphe passe d'une position concave vers le haut à une position concave vers le bas. C'est là que la « stabilisation » commence à se produire, car le taux de croissance net ralentit à mesure que la population commence à se rapprocher de la capacité de charge.

Exercice$\PageIndex{1}$

On observe qu'une population de lapins vivant dans un pré est parfois$200$ constituée de lapins$t=0$. Après un mois, on observe que la population de lapins a augmenté de$4%$. En utilisant une population initiale$200$ et un taux de croissance de$0.04$, avec une capacité de charge de$750$ lapins,

Écrivez l'équation différentielle logistique et la condition initiale pour ce modèle.
Tracez un champ de pente pour cette équation différentielle logistique et esquissez la solution correspondant à une population initiale de$200$ lapins.
Résolvez le problème de la valeur initiale pour$P(t)$.
Utilisez la solution pour prévoir la population après une$1$ année.

Allusion: Déterminez d'abord les valeurs de$r,K,$ et$P_0$. Créez ensuite le problème de valeur initiale, dessinez le champ de direction et résolvez le problème.

Réponse

un.$\dfrac{dP}{dt}=0.04(1−\dfrac{P}{750}),P(0)=200$

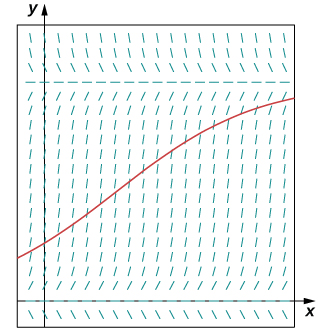
$Un champ de direction avec des lignes horizontales sur l'axe x et y = 15. Les autres lignes sont verticales, à l'exception de celles qui suivent l'axe x et y = 15. Une solution est dessinée qui traverse l'axe y à environ (0, 4) et se rapproche asymptotiquement de y = 15.$

c.$P(t)=\dfrac{3000e^{.04t}}{11+4e^{.04t}}$

d. Après des$12$ mois, la population sera composée de$P(12)≈278$ lapins.

Projet étudiant : Équation logistique avec un seuil de population

Une amélioration du modèle logistique inclut un seuil de population. La population seuil est définie comme étant la population minimale nécessaire à la survie de l'espèce. Nous utilisons la variable$T$ pour représenter la population seuil. Une équation différentielle qui intègre à la fois le seuil de population$T$ et la capacité de charge$K$ est

\[ \dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right) \nonumber \]

où$r$ représente le taux de croissance, comme précédemment.

Le seuil de population est utile aux biologistes et peut être utilisé pour déterminer si une espèce donnée doit être inscrite sur la liste des espèces menacées. Un groupe de chercheurs australiens affirme avoir déterminé le seuil de population pour la survie de n'importe quelle espèce :$5000$ les adultes. (Catherine Clabby, « A Magic Number », American Scientist 98 (1) : 24, doi : 10.1511/2010.82.24. Consulté le 9 avril 2015, www.americanscientist.org/iss... a-magic-number). C'est pourquoi nous utilisons$T=5000$ comme seuil de population dans ce projet. Supposons que la capacité de charge environnementale du wapiti dans l'environnement du Montana soit de$25,000$. Configurez l'équation en utilisant la capacité de charge$25,000$ et la population seuil de$5000$. Supposons un taux de croissance annuel net de 18 %.
Dessinez le champ de direction de l'équation différentielle à partir de l'étape$1$, ainsi que plusieurs solutions pour différentes populations initiales. Quelles sont les solutions constantes de l'équation différentielle ? À quoi correspondent ces solutions dans le modèle de population original (c'est-à-dire dans un contexte biologique) ?
Quelle est la population limite pour chaque population initiale que vous avez choisie au cours de l'étape$2$ ? (Conseil : utilisez le champ de pente pour voir ce qui se passe pour les différentes populations initiales, c'est-à-dire rechercher les asymptotes horizontales de vos solutions.)
Cette équation peut être résolue en utilisant la méthode de séparation des variables. Cependant, il est très difficile d'obtenir la solution en tant que fonction explicite de$t$. À l'aide d'une population initiale de$18,000$ wapitis, résolvez le problème de la valeur initiale et exprimez la solution en fonction implicite de t, ou résolvez le problème général de la valeur initiale en trouvant une solution en termes de$r,K,T,$ et$P_0$.

Concepts clés

Lors de l'étude des fonctions démographiques, différentes hypothèses, telles que la croissance exponentielle, la croissance logistique ou le seuil de population, conduisent à des taux de croissance différents.
L'équation différentielle logistique intègre le concept de capacité de charge. Cette valeur est une valeur limite de la population pour un environnement donné.
L'équation différentielle logistique peut être résolue pour tout taux de croissance positif, population initiale et capacité de charge.

Équations clés

Équation différentielle logistique et problème de valeur initiale

$\dfrac{dP}{dt}=rP\left(1−\dfrac{P}{K}\right),\quad P(0)=P_0$

Solution au problème de l'équation différentielle logistique et de la valeur initiale

$P(t)=\dfrac{P_0Ke^{rt}}{(K−P_0)+P_0e^{rt}}$

Modèle de population seuil

$\dfrac{dP}{dt}=−rP\left(1−\dfrac{P}{K}\right)\left(1−\dfrac{P}{T}\right)$

Lexique

capacité de charge: la population maximale d'un organisme que l'environnement peut maintenir indéfiniment

taux de croissance: la constante$r>0$ de la fonction de croissance exponentielle$P(t)=P_0e^{rt}$

population initiale: la population de l'époque$t=0$

équation différentielle logistique: une équation différentielle qui intègre la capacité de charge$K$ et le taux de croissance rr dans un modèle de population

ligne de phase: une représentation visuelle du comportement des solutions à une équation différentielle autonome soumise à diverses conditions initiales

population seuil: la population minimale nécessaire à la survie d'une espèce

Définition : Capacité de charge

Définition : Équation différentielle logistique

Exemple\(\PageIndex{1}\): Examining the Carrying Capacity of a Deer Population

Solution de l'équation différentielle logistique

Exercice\(\PageIndex{1}\)

Projet étudiant : Équation logistique avec un seuil de population