Skip to main content
Global

5.7E : Exercices pour la section 5.7

  1. Last updated
  2. Save as PDF
  • Page ID
    197373

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 6, évaluez chaque intégrale en fonction d'une fonction trigonométrique inverse.

    1)\(\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}}\)

    Réponse
    \(\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}} \quad = \quad \sin^{−1}x\bigg|^{\sqrt{3}/2}_0=\dfrac{π}{3}\)

    2)\(\displaystyle ∫^{1/2}_{−1/2}\frac{dx}{\sqrt{1−x^2}}\)

    3)\(\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}}\)

    Réponse
    \(\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}} \quad = \quad \tan^{−1}x\bigg|^1_{\sqrt{3}}=−\dfrac{π}{12}\)

    4)\(\displaystyle ∫^{\sqrt{3}}_{\frac{1}{\sqrt{3}}}\frac{dx}{1+x^2}\)

    5)\(\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}}\)

    Réponse
    \(\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}} \quad = \quad \sec^{−1}x\bigg|^{\sqrt{2}}_1=\dfrac{π}{4}\)

    6)\(\displaystyle ∫^{\frac{2}{\sqrt{3}}}_1\frac{dx}{|x|\sqrt{x^2−1}}\)

    Dans les exercices 7 à 12, trouvez chaque intégrale indéfinie en utilisant les substitutions appropriées.

    7)\(\displaystyle ∫\frac{dx}{\sqrt{9−x^2}}\)

    Réponse
    \(\displaystyle ∫\frac{dx}{\sqrt{9−x^2}} \quad = \quad \sin^{−1}\left(\frac{x}{3}\right)+C\)

    8)\(\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}}\)

    9)\(\displaystyle ∫\frac{dx}{9+x^2}\)

    Réponse
    \(\displaystyle ∫\frac{dx}{9+x^2} \quad = \quad \frac{1}{3}\tan^{−1}\left(\frac{x}{3}\right)+C\)

    10)\(\displaystyle ∫\frac{dx}{25+16x^2}\)

    11)\(\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}}\)

    Réponse
    \(\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}} \quad = \quad \frac{1}{3}\sec^{−1}\left(\frac{|x|}{3}\right)+C\)

    (12)\(\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}}\)

    13) Expliquez la relation.\(\displaystyle −\cos^{−1}t+C=∫\frac{dt}{\sqrt{1−t^2}}=\sin^{−1}t+C.\) Est-ce vrai, en général, cela\(\cos^{−1}t=−\sin^{−1}t\) ?

    Réponse
    \(\cos(\frac{π}{2}−θ)=\sin θ.\)Donc,\(\sin^{−1}t=\dfrac{π}{2}−\cos^{−1}t.\) ils diffèrent par une constante.

    14) Expliquez la relation.\(\displaystyle \sec^{−1}t+C=∫\frac{dt}{|t|\sqrt{t^2−1}}=−\csc^{−1}t+C.\) Est-ce vrai, en général, cela\(\sec^{−1}t=−\csc^{−1}t\) ?

    15) Expliquez ce qui ne va pas avec l'intégrale suivante :\(\displaystyle ∫^2_1\frac{dt}{\sqrt{1−t^2}}\).

    Réponse
    \(\sqrt{1−t^2}\)n'est pas défini comme un nombre réel lorsque\(t>1\).

    16) Expliquez ce qui ne va pas avec l'intégrale suivante :\(\displaystyle ∫^1_{−1}\frac{dt}{|t|\sqrt{t^2−1}}\).

    Réponse
    \(\sqrt{t^2−1}\)n'est pas défini comme un nombre réel quand\(-1 \lt t \lt 1\), et l'integrand n'est pas défini quand\(t = -1\) ou\(t = 1\).

    Dans les exercices 17 à 20, déterminez l'antidérivée de\(f\) avec\(C=0\), puis utilisez une calculatrice pour représenter\(f\) graphiquement et l'antidérivée sur l'intervalle donné\([a,b]\). Identifiez une valeur\(C\) telle que l'ajout\(C\) à l'antidérivé permet de récupérer l'intégrale définie\(\displaystyle F(x)=∫^x_af(t)\,dt\).

    17) [T]\(\displaystyle ∫\frac{1}{\sqrt{9−x^2}}\,dx\) over\([−3,3]\)

    Réponse

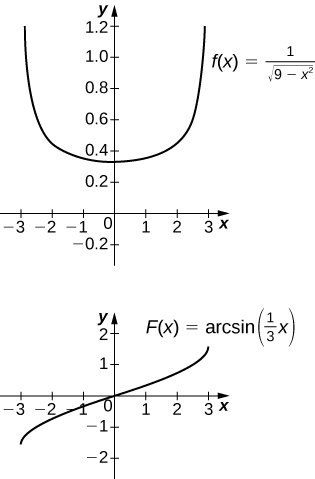
    Deux graphiques. La première montre la fonction f (x) = 1/sqrt (9 — x^2). Il s'agit d'une courbe d'ouverture vers le haut symétrique par rapport à l'axe y, se croisant en (0, 1/3). La seconde montre la fonction F (x) = arcsin (1/3 x). Il s'agit d'une courbe croissante passant par l'origine.

    L'antidérivé est\( \sin^{−1}(\frac{x}{3})+C\). La prise\(C=\frac{π}{2}\) permet de récupérer l'intégrale définie.

    18) [T]\(\displaystyle ∫\frac{9}{9+x^2}\,dx\) over\([−6,6]\)

    19) [T]\(\displaystyle ∫\frac{\cos x}{4+\sin^2x}\,dx\) over\([−6,6]\)

    Réponse

    Deux graphiques. La première montre la fonction f (x) = cos (x)/(4+ sin (x) ^2). Il s'agit d'une fonction oscillante sur [-6, 6] avec des points de retournement approximativement à (-3, -2,5), (0, 0,25) et (3, -2,5), où (0, 0,25) est un maximum local et les autres sont des minutes locales. La seconde montre la fonction F (x) = 0,5 * arctan (.5*sin (x)), qui oscille également au-dessus de [-6,6]. Ses points de retournement se situent approximativement à (-4,5, 0,25), (-1,5, -0,25), (1,5, 0,25) et (4,5, -0,25).

    L'antidérivé est\(\frac{1}{2}\tan^{−1}(\frac{\sin x}{2})+C\). La prise\(C=\frac{1}{2}\tan^{−1}(\frac{\sin(6)}{2})\) permet de récupérer l'intégrale définie.

    20) [T]\(\displaystyle ∫\frac{e^x}{1+e^{2x}}\,dx\) plus\([−6,6]\)

    Dans les exercices 21 à 26, calculez l'antidérivé en utilisant les substitutions appropriées.

    (21)\(\displaystyle ∫\frac{\sin^{−1}t}{\sqrt{1−t^2}}\,dt\)

    Réponse
    \(\displaystyle ∫\frac{\sin^{−1}t\,dt}{\sqrt{1−t^2}} \quad = \quad \tfrac{1}{2}(\sin^{−1}t)^2+C\)

    (22)\(\displaystyle ∫\frac{dt}{\sin^{−1} t\sqrt{1−t^2}}\)

    23)\(\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt\)

    Réponse
    \(\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt \quad = \quad \frac{1}{4}(\tan^{−1}(2t))^2+C\)

    (24)\(\displaystyle ∫\frac{t\tan^{−1}(t^2)}{1+t^4}\,dt\)

    25)\(\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt\)

    Réponse
    \(\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt \quad = \quad \tfrac{1}{4}(\sec^{−1}\left(\tfrac{t}{2}\right))^2+C\)

    (26)\(\displaystyle ∫\frac{t\sec^{−1}(t^2)}{t^2\sqrt{t^4−1}}\,dt\)

    Dans les exercices 27 à 32, utilisez une calculatrice pour représenter graphiquement l'antidérivée de\(f\) avec\(C=0\) sur l'intervalle donné.\([a,b].\) Approximez une valeur de\(C\), si possible, de telle sorte que l'addition\(C\) à l'antidérivée donne la même valeur que l'intégrale définie.\(\displaystyle F(x)=∫^x_af(t)\,dt.\)

    27) [T]\(\displaystyle ∫\frac{1}{x\sqrt{x^2−4}}\,dx\) over\([2,6]\)

    Réponse

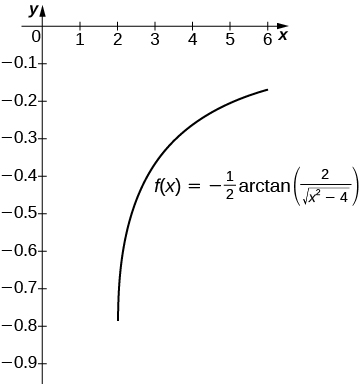
    Un graphique de la fonction f (x) = -,5 * arctan (2/(sqrt (x^2 — 4))) dans le quadrant quatre. Il s'agit d'une courbe descendante concave croissante avec une asymptote verticale à x=2.

    L'antidérivé est\(\frac{1}{2}\sec^{−1}(\frac{x}{2})+C\). La prise\(C=0\) permet de récupérer l'intégrale définitive\( [2,6]\).

    28) [T]\(\displaystyle ∫\frac{1}{(2x+2)\sqrt{x}}\,dx\) over\([0,6]\)

    29) [T]\(\displaystyle ∫\frac{(\sin x+x\cos x)}{1+x^2\sin^2x\,dx}\) over\( [−6,6]\)

    Réponse

    Le graphique de f (x) = arctan (x sin (x)) sur [-6,6]. Il possède cinq points de retournement à environ (-5, -1,5), (-2,1), (0,0), (2,1) et (5, -1,5).

    L'antidérivé général est\(\tan^{−1}(x\sin x)+C\). La prise\(C=−\tan^{−1}(6\sin(6))\) permet de récupérer l'intégrale définie.

    30) [T]\(\displaystyle ∫\frac{2e^{−2x}}{\sqrt{1−e^{−4x}}}\,dx\) plus\([0,2]\)

    31) [T]\(\displaystyle ∫\frac{1}{x+x\ln 2x}\) plus\([0,2]\)

    Réponse

    Un graphe de la fonction f (x) = arctan (ln (x)) sur (0, 2]. Il s'agit d'une courbe croissante avec une intersection X à (1,0).

    L'antidérivé général est\(\tan^{−1}(\ln x)+C\). La prise\(\displaystyle C=\tfrac{π}{2}=\lim_{t \to ∞}\tan^{−1} t\) permet de récupérer l'intégrale définie.

    32) [T]\(\displaystyle ∫\frac{\sin^{−1}x}{\sqrt{1−x^2}}\) plus\([−1,1]\)

    Dans les exercices 33 à 38, calculez chaque intégrale en utilisant les substitutions appropriées.

    33)\(\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt\)

    Réponse
    \(\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \sin^{−1}(e^t)+C\)

    34)\(\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt\)

    35)\(\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}}\)

    Réponse
    \(\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}} \quad = \quad \sin^{−1}(\ln t)+C\)

    36)\(\displaystyle ∫\frac{dt}{t(1+\ln^2t)}\)

    (37)\(\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt\)

    Réponse
    \(\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt \quad = \quad −\frac{1}{2}(\cos^{−1}(2t))^2+C\)

    38)\(\displaystyle ∫\frac{e^t\cos^{−1}(e^t)}{\sqrt{1−e^{2t}}}\,dt\)

    Dans les exercices 39 à 42, calculez chaque intégrale définie.

    39)\(\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt\)

    Réponse
    \(\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt \quad = \quad \frac{1}{2}\ln\left(\frac{4}{3}\right)\)

    40)\(\displaystyle ∫^{1/2}_{1/4}\frac{\tan(\cos^{−1}t)}{\sqrt{1−t^2}}\,dt\)

    41)\(\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt\)

    Réponse
    \(\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt \quad = \quad 1−\frac{2}{\sqrt{5}}\)

    (42)\(\displaystyle ∫^{1/2}_0\frac{\cos(\tan^{−1}t)}{1+t^2}\,dt\)

    43) Pour\(A>0\), calculez\(\displaystyle I(A)=∫^{A}_{−A}\frac{dt}{1+t^2}\) et évaluez\(\displaystyle \lim_{a→∞}I(A)\), l'aire sous le graphique de\(\dfrac{1}{1+t^2}\)\([−∞,∞]\).

    Réponse
    \(2\tan^{−1}(A)→π\)comme\(A→∞\)

    44) Pour\(1<B<∞\), calculez\(\displaystyle I(B)=∫^B_1\frac{dt}{t\sqrt{t^2−1}}\) et évaluez\(\displaystyle \lim_{B→∞}I(B)\), l'aire sous le graphique de\(\frac{1}{t\sqrt{t^2−1}}\) plus\([1,∞)\).

    45) Utilisez la substitution\(u=\sqrt{2}\cot x\) et l'identité\(1+\cot^2x=\csc^2x\) pour évaluer\(\displaystyle ∫\frac{dx}{1+\cos^2x}\). (Conseil : multipliez le haut et le bas de l'integrand par\(\csc^2x\).)

    Réponse
    En utilisant l'astuce, on a\(\displaystyle ∫\frac{\csc^2x}{\csc^2x+\cot^2x}\,dx=∫\frac{\csc^2x}{1+2\cot^2x}\,dx.\) Set\(u=\sqrt{2}\cot x.\) Then,\(du=−\sqrt{2}\csc^2x\) et l'intégrale est\(\displaystyle −\tfrac{1}{\sqrt{2}}∫\frac{du}{1+u^2}=−\tfrac{\sqrt{2}}{2}\tan^{−1}u+C=\tfrac{\sqrt{2}}{2}\tan^{−1}(\sqrt{2}\cot x)+C\). Si l'on utilise l'identité\(\tan^{−1}s+\tan^{−1}(\frac{1}{s})=\frac{π}{2}\), elle peut également être écrite\(\tfrac{\sqrt{2}}{2}\tan^{−1}(\frac{\tan x}{\sqrt{2}})+C.\)

    46) [T] Approximez les points auxquels les graphes de\(f(x)=2x^2−1\) et\(g(x)=(1+4x^2)^{−3/2}\) se croisent, et approximez l'aire entre leurs graphes avec une précision de trois décimales.

    47) [T] Approximez les points auxquels les graphes de\(f(x)=x^2−1\) et\(f(x)=x^2−1\) se croisent, et approximez l'aire entre leurs graphes avec une précision de trois décimales.

    Réponse
    \(x≈±1.13525.\)L'estimation du point final de gauche avec\(N=100\) est de 2,796 et ces décimales persistent pour\(N=500\).

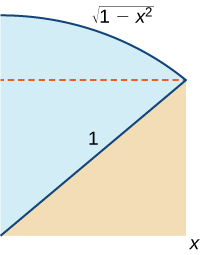
    48) Utilisez le graphique suivant pour prouver que\(\displaystyle ∫^x_0\sqrt{1−t^2}\,dt=\frac{1}{2}x\sqrt{1−x^2}+\frac{1}{2}\sin^{−1}x.\)

    Un diagramme contenant deux formes, un coin d'un cercle ombré en bleu au-dessus d'un triangle ombré en brun. L'hypoténuse du triangle est l'un des rayons du coin du cercle et mesure 1 unité de long. Une ligne rouge pointillée forme un rectangle à partir d'une partie du coin et du triangle, l'hypoténuse du triangle constituant la diagonale du rectangle. La courbe du cercle est décrite par l'équation sqrt (1-x^2).