5.6E : Exercices pour la section 5.6

Last updated
Save as PDF

Page ID: 197351

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pour les exercices 1 à 8, calculez chaque intégrale indéfinie.

1)$\displaystyle ∫e^{2x}\,dx$

2)$\displaystyle ∫e^{−3x}\,dx$

Réponse: $\displaystyle ∫e^{−3x}\,dx \quad = \quad \frac{−1}{3}e^{−3x}+C$

3)$\displaystyle ∫2^x\,dx$

4)$\displaystyle ∫3^{−x}\,dx$

Réponse: $\displaystyle ∫3^{−x}\,dx \quad = \quad −\frac{3^{−x}}{\ln 3}+C$

5)$\displaystyle ∫\frac{1}{2x}\,dx$

6)$\displaystyle ∫\frac{2}{x}\,dx$

Réponse: $\displaystyle ∫\frac{2}{x}\,dx \quad = \quad 2\ln x+C \quad = \quad \ln(x^2)+C$

7)$\displaystyle ∫\frac{1}{x^2}\,dx$

8)$\displaystyle ∫\frac{1}{\sqrt{x}}\,dx$

Réponse: $\displaystyle ∫\frac{1}{\sqrt{x}}\,dx \quad = \quad 2\sqrt{x}+C$

Dans les exercices 9 à 16, trouvez chaque intégrale indéfinie en utilisant les substitutions appropriées.

9)$\displaystyle ∫\frac{\ln x}{x}\,dx$

10)$\displaystyle ∫\frac{dx}{x(\ln x)^2}$

Réponse: $\displaystyle ∫\frac{dx}{x(\ln x)^2} \quad = \quad −\frac{1}{\ln x}+C$

11)$\displaystyle ∫\frac{dx}{x\ln x}\quad (x>1)$

(12)$\displaystyle ∫\frac{dx}{x\ln x\ln(\ln x)}$

Réponse: $\displaystyle ∫\frac{dx}{x\ln x\ln(\ln x)} \quad = \quad \ln(\ln(\ln x))+C$

13)$\displaystyle ∫\tan θ\,dθ$

(14)$\displaystyle ∫\frac{\cos x−x\sin x}{x\cos x}\,dx$

Réponse: $\displaystyle ∫\frac{\cos x−x\sin x}{x\cos x}\,dx \quad = \quad \ln(x\cos x)+C$

(15)$\displaystyle ∫\frac{\ln(\sin x)}{\tan x}\,dx$

16)$\displaystyle ∫\ln(\cos x)\tan x\,dx$

Réponse: $\displaystyle ∫\ln(\cos x)\tan x\,dx \quad = \quad −\dfrac{1}{2}(\ln(\cos(x)))^2+C$

17)$\displaystyle ∫xe^{−x^2}\,dx$

18)$\displaystyle ∫x^2e^{−x^3}\,dx$

Réponse: $\displaystyle ∫x^2e^{−x^3}\,dx \quad = \quad \dfrac{−e^{−x^3}}{3}+C$

19)$\displaystyle ∫e^{\sin x}\cos x\,dx$

(20)$\displaystyle ∫e^{\tan x}\sec^2 x\,dx$

Réponse: $\displaystyle ∫e^{\tan x}\sec^2 x\,dx\quad = \quad e^{\tan x}+C$

(21)$\displaystyle ∫\frac{e^{\ln x}}{x}\,dx $

(22)$\displaystyle ∫\frac{e^{\ln(1−t)}}{1−t}\,dt$

Réponse: $\displaystyle ∫\frac{e^{\ln(1−t)}}{1−t}\,dt = \int \frac{1-t}{1-t}\,dt = \int 1\, dt \quad = \quad t+C$

Dans les exercices 23 à 28, vérifiez cela par différenciation$\displaystyle ∫\ln x\,dx=x(\ln x−1)+C$, puis utilisez les modifications appropriées des variables pour calculer l'intégrale.

23)$\displaystyle ∫\ln x\,dx$ (Astuce :$\displaystyle ∫\ln x\,dx=\frac{1}{2}∫x\ln(x^2)\,dx$)

(24)$\displaystyle ∫x^2\ln^2 x\,dx$

Réponse: $\displaystyle ∫x^2\ln^2 x\,dx \quad = \quad \dfrac{1}{9}x^3(\ln(x^3)−1)+C$

25)$\displaystyle ∫\frac{\ln x}{x^2}\,dx$ (Indice : Set)$u=\dfrac{1}{x}.)$

26)$\displaystyle ∫\frac{\ln x}{\sqrt{x}}\,dx$ (Indice : Set)$u=\sqrt{x}.)$

Réponse: $ \displaystyle ∫\frac{\ln x}{\sqrt{x}}\,dx \quad = \quad 2\sqrt{x}(\ln x−2)+C$

27) Écrivez une intégrale pour exprimer l'aire sous le graphe$y=\dfrac{1}{t}$ de$ t=1$ à$e^x$ et évaluez l'intégrale.

28) Écrivez une intégrale pour exprimer l'aire sous le graphe$y=e^t$ entre$t=0$ et$t=\ln x$, et évaluez l'intégrale.

Réponse: $\displaystyle ∫^{\ln x}_0e^t\,dt=e^t\bigg|^{\ln x}_0=e^{\ln x}−e^0=x−1$

Dans les exercices 29 à 35, utilisez des substitutions appropriées pour exprimer les intégrales trigonométriques en termes de compositions avec des logarithmes.

(29)$\displaystyle ∫\tan(2x)\,dx$

(30)$\displaystyle ∫\frac{\sin(3x)−\cos(3x)}{\sin(3x)+\cos(3x)}\,dx$

Réponse: $ \displaystyle ∫\frac{\sin(3x)−\cos(3x)}{\sin(3x)+\cos(3x)}\,dx \quad = \quad −\frac{1}{3}\ln|\sin(3x)+\cos(3x)| + C$

31)$\displaystyle ∫\frac{x\sin(x^2)}{\cos(x^2)}\,dx$

32)$\displaystyle ∫x\csc(x^2)\,dx$

Réponse: $ \displaystyle ∫x\csc(x^2)\,dx \quad = \quad −\frac{1}{2}\ln∣\csc(x^2)+\cot(x^2)∣+C$

33)$\displaystyle ∫\ln(\cos x)\tan x\,dx$

34)$\displaystyle ∫\ln(\csc x)\cot x\,dx$

Réponse: $ \displaystyle ∫\ln(\csc x)\cot x\,dx \quad = \quad −\frac{1}{2}(\ln(\csc x))^2+C$

35)$\displaystyle ∫\frac{e^x−e^{−x}}{e^x+e^{−x}}\,dx$

Dans les exercices 36 à 40, évaluez l'intégrale définie.

36)$\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}\,dx$

Réponse: $\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}\,dx \quad = \quad \frac{1}{3}\ln\left(\tfrac{26}{7}\right)$

(37)$\displaystyle ∫^{π/4}_0\tan x\,dx$

38)$\displaystyle ∫^{π/3}_0\frac{\sin x−\cos x}{\sin x+\cos x}\,dx$

Réponse: $\displaystyle ∫^{π/3}_0\frac{\sin x−\cos x}{\sin x+\cos x}\,dx \quad = \quad \ln(\sqrt{3}−1)$

39)$\displaystyle ∫^{π/2}_{π/6}\csc x\,dx$

40)$\displaystyle ∫^{π/3}_{π/4}\cot x\,dx$

Réponse: $\displaystyle ∫^{π/3}_{π/4}\cot x\,dx \quad = \quad \frac{1}{2}\ln\frac{3}{2}$

Dans les exercices 41 à 46, intégrez en utilisant la substitution indiquée.

41)$\displaystyle ∫\frac{x}{x−100}\,dx;\quad u=x−100$

(42)$\displaystyle ∫\frac{y−1}{y+1}\,dy;\quad u=y+1$

Réponse: $ \displaystyle ∫\frac{y−1}{y+1}\,dy \quad = \quad y−2\ln|y+1|+C$

43)$\displaystyle ∫\frac{1−x^2}{3x−x^3}\,dx;\quad u=3x−x^3$

44)$\displaystyle ∫\frac{\sin x+\cos x}{\sin x−\cos x}\,dx;\quad u=\sin x−\cos x$

Réponse: $\displaystyle ∫\frac{\sin x+\cos x}{\sin x−\cos x}\,dx \quad=\quad \ln|\sin x−\cos x|+C$

45)$\displaystyle ∫e^{2x}\sqrt{1−e^{2x}}\,dx;\quad u=e^{2x}$

46)$\displaystyle ∫\ln(x)\frac{\sqrt{1−(\ln x)^2}}{x}\,dx;\quad u=\ln x$

Réponse: $\displaystyle ∫\ln(x)\frac{\sqrt{1−(\ln x)^2}}{x}\,dx \quad = \quad −\frac{1}{3}(1−(\ln x^2))^{3/2}+C$

47)$\displaystyle \int \frac{\sqrt{x}}{\sqrt{x} + 2}\,dx; \quad u = \sqrt{x} + 2$

Réponse: $\displaystyle \int \frac{\sqrt{x}}{\sqrt{x} + 2}\,dx \quad = \quad \left( \sqrt{x} + 2 \right)^2 - 8\left( \sqrt{x} + 2 \right) + 8\ln\left( \sqrt{x} + 2 \right) + C$

48)$\displaystyle \int e^x\sec(e^x+1)\tan(e^x+1)\,dx; \quad u = e^{x} + 1$

Réponse: $\displaystyle \int e^x\sec(e^x+1)\tan(e^x+1)\,dx \quad = \quad \sec(e^x+1) + C$

Dans les exercices 49 à 54, déterminez si l'approximation de l'extrémité droite surestime ou sous-estime la surface exacte. Calculez ensuite la bonne estimation du point final$R_{50}$ et résolvez la zone exacte.

49) [T]$y=e^x$ over$[0,1]$

50) [T]$ y=e^{−x}$ plus$[0,1]$

Réponse: Comme elle$f$ est en baisse, l'estimation du bon paramètre sous-estime la superficie.
Solution exacte :$\dfrac{e−1}{e},\quad R_{50}=0.6258$.

51) [T]$y=\ln(x)$ plus$[1,2]$

52) [T]$y=\dfrac{x+1}{x^2+2x+6}$ over$ [0,1]$

Réponse: Depuis qu'elle$f$ augmente, l'estimation du bon paramètre surestime la superficie.
Solution exacte :$\dfrac{2\ln(3)−\ln(6)}{2},\quad R_{50}=0.2033.$

53) [T]$y=2^x$ plus$[−1,0]$

54) [T]$ y=−2^{−x}$ plus$ [0,1]$

Réponse: Puisque$f$ cette valeur augmente, l'estimation du bon paramètre surestime la superficie (la superficie réelle est un nombre négatif plus élevé).
Solution exacte :$−\dfrac{1}{\ln(4)},\quad R_{50}=−0.7164.$

Dans les exercices 55 à 58,$f(x)≥0$ pour$a≤x≤b$. Trouvez l'aire sous le graphique$f(x)$ entre les valeurs données$a$ et$b$ en intégrant.

55)$f(x)=\dfrac{\log_{10}(x)}{x};\quad a=10,b=100$

(56)$f(x)=\dfrac{\log_2(x)}{x};\quad a=32,b=64$

Réponse: $\dfrac{11}{2}\ln 2$

(57)$f(x)=2^{−x};\quad a=1,b=2$

58)$f(x)=2^{−x};\quad a=3,b=4$

Réponse: $\dfrac{1}{\ln(65,536)}$

59) Trouvez l'aire sous le graphique de la fonction$ f(x)=xe^{−x^2}$ entre$x=0$ et$x=5$.

60) Calculez l'intégrale de$f(x)=xe^{−x^2}$ et trouvez la plus petite valeur de$N$ telle sorte que l'aire sous le graphique$f(x)=xe^{−x^2}$ entre$ x=N$ et$x=N+10$ soit au plus$0.01$.

Réponse: $\displaystyle ∫^{N+1}_Nxe^{−x^2}\,dx=\frac{1}{2}(e^{−N^2}−e^{−(N+1)^2}).$La quantité est moindre que$0.01$ lorsque$N=2$.

61) Trouvez la limite, comme$N$ tend vers l'infini, de l'aire sous le graphique$f(x)=xe^{−x^2}$ entre$x=0$ et$x=5$.

62) Montrez cela$\displaystyle ∫^b_a\frac{dt}{t}=∫^{1/a}_{1/b}\frac{dt}{t}$ quand$0<a≤b$.

Réponse: $\displaystyle ∫^b_a\frac{dx}{x}=\ln(b)−\ln(a)=\ln(\frac{1}{a})−\ln(\frac{1}{b})=∫^{1/a}_{1/b}\frac{dx}{x}$

63) Supposons que$f(x)>0$ pour tous$x$$f$ et cela$g$ soient différenciables. Utilisez l'identité$ f^g=e^{g\ln f}$ et la règle de chaîne pour trouver la dérivée de$ f^g$.

64) Utilisez l'exercice précédent pour trouver l'antidérivé de$h(x)=x^x(1+\ln x)$ et évaluer$\displaystyle ∫^3_2x^x(1+\ln x)\,dx$.

Réponse: 23

65) Montrez que si$c>0$, alors l'intégrale$\frac{1}{x}$ de de$ac$ à$bc$ $(\text{for}\,0<a<b)$est la même que l'intégrale de$\frac{1}{x}$ de$a$ à $b$.

Les exercices suivants visent à dériver les propriétés fondamentales du logarithme naturel à partir de la définition$\displaystyle \ln(x)=∫^x_1\frac{dt}{t}$, en utilisant les propriétés de l'intégrale définie et en ne faisant aucune autre hypothèse.

66) Utilisez l'identité$\displaystyle \ln(x)=∫^x_1\frac{dt}{t}$ pour obtenir l'identité$\ln\left(\dfrac{1}{x}\right)=−\ln x$.

Réponse: Nous pouvons supposer que$x>1$,$\dfrac{1}{x}<1.$ alors,$\displaystyle ∫^{1/x}_{1}\frac{dt}{t}$. Effectuez maintenant la substitution$u=\dfrac{1}{t}$, so$du=−\dfrac{dt}{t^2}$ et$\dfrac{du}{u}=−\dfrac{dt}{t}$, et modifiez les points de terminaison :$\displaystyle ∫^{1/x}_1\frac{dt}{t}=−∫^x_1\frac{du}{u}=−\ln x.$

67) Utilisez un changement de variable dans l'intégrale$\displaystyle ∫^{xy}_1\frac{1}{t}\,dt$ pour montrer que$\ln xy=\ln x+\ln y$ pour$ x,y>0$.

68) Utilisez l'identité$\displaystyle \ln x=∫^x_1\frac{dt}{x}$ pour montrer qu'il$\ln(x)$ s'agit d'une fonction croissante de$x$ on$[0,∞)$, et utilisez les exercices précédents pour montrer que la plage de$\ln(x)$ est$(−∞,∞)$. Sans autres hypothèses, concluez$\ln(x)$ que la fonction inverse est définie sur$ (−∞,∞).$

69) Supposons, pour le moment, que nous ne savons pas que$e^x$ c'est la fonction inverse de$\ln(x)$, mais gardez à l'esprit$\ln(x)$ qu'une fonction inverse est définie sur$ (−∞,∞)$. Appelle-le$E$. Utilisez l'identité$\ln xy=\ln x+\ln y$ pour déduire cela$E(a+b)=E(a)E(b)$ pour tous les nombres réels$a$,$b$.

70) Supposons, pour le moment, que nous ne savons pas que$ e^x$ c'est la fonction inverse de$\ln x$, mais gardez à l'esprit$ \ln x$ qu'une fonction inverse est définie sur$(−∞,∞)$. Appelle-le$E$. Montrez que$E'(t)=E(t).$

Réponse: $x=E(\ln(x)).$Alors,$1=\dfrac{E'(\ln x)}{x}$ ou$x=E'(\ln x)$. Puisque n'importe quel nombre$t$ peut être écrit$t=\ln x$ pour certains$x$, et pour cela$t$ nous l'avons fait$x=E(t)$, il s'ensuit que pour tout$t,\,E'(t)=E(t).$

71) L'intégrale sinusoïdale, définie comme$\displaystyle S(x)=∫^x_0\frac{\sin t}{t}\,dt$ étant une quantité importante en ingénierie. Bien qu'il ne dispose pas d'une formule fermée simple, il est possible d'estimer son comportement pour les grandes$x$. Montrez cela pour$k≥1,\quad |S(2πk)−S(2π(k+1))|≤\dfrac{1}{k(2k+1)π}.$ (Astuce :$ \sin(t+π)=−\sin t$)

72) [T] La distribution normale de probabilité est donnée par$p(x)=\dfrac{1}{σ\sqrt{2π}}e^{−(x−μ)^2/2σ^2}$, où$σ$ sont l'écart type et$μ$ la moyenne. La distribution normale standard en termes de probabilité$p_s$, correspond à$ μ=0$ et$σ=1$. Calculez les estimations du point final gauche$R_{10}$ et$R_{100}$ de$\displaystyle ∫^1_{−1}\frac{1}{\sqrt{2π}}e^{−x^{2/2}}\,dx.$

Réponse: $R_{10}=0.6811,\quad R_{100}=0.6827$

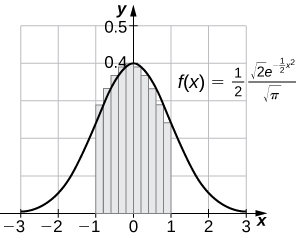
$Un graphique de la fonction f (x) = 0,5 * (sqrt (2) *e^ (-0,5x^2))/sqrt (pi). Il s'agit d'une courbe d'ouverture vers le bas qui est symétrique sur l'axe y, se croisant à environ (0,4). Il approche 0 lorsque x passe à l'infini positif et négatif. Entre 1 et -1, dix rectangles sont dessinés pour une estimation de l'extrémité droite de l'aire sous la courbe.$

73) [T] Calculez les bonnes estimations du point final$R_{50}$ et$R_{100}$ de$\displaystyle ∫^5_{−3}\frac{1}{2\sqrt{2π}}e^{−(x−1)^2/8}$.

Contributeurs et attributions

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added problems 47-48 to Section 5.6 exercises.