4.11 : Chapitre 4 : Exercices de révision

Last updated
Save as PDF

Page ID: 197607

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Vrai ou faux ? Justifiez votre réponse par une preuve ou un contre-exemple. Supposons que$f(x)$ c'est continu et différenciable, sauf indication contraire.

1) Si$f(−1)=−6$ oui$f(1)=2$, alors il existe au moins un point$x∈[−1,1]$ tel que$f′(x)=4.$

Réponse: Vrai, selon le théorème des valeurs moyennes

2) S'$f′(c)=0,$il y a un maximum ou un minimum à$x=c.$

3) Il existe une fonction telle que$f(x)<0,f′(x)>0,$ et$f''(x)<0.$ (Une « preuve » graphique est acceptable pour cette réponse.)

Réponse: Vrai

4) Il existe une fonction telle qu'il existe à la fois un point d'inflexion et un point critique pour une certaine valeur$x=a.$

5) Sur la base du graphique de$f′$, déterminez où$f$ augmente ou diminue.

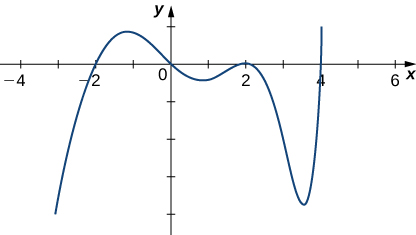
$La fonction augmente pour traverser l'axe X en -2, atteint un maximum puis diminue par l'origine, atteint un minimum puis augmente jusqu'à un maximum en 2, diminue jusqu'à un minimum puis augmente pour passer par l'axe x en 4 et continue d'augmenter.$

Réponse: En hausse :$(−2,0)∪(4,∞)$, en baisse :$(−∞,−2)∪(0,4)$

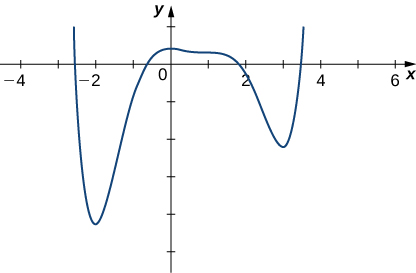
6) Le graphique de$f$ est donné ci-dessous. Dessiner$f′$.

$La fonction décroît rapidement et atteint un minimum local à −2, puis elle augmente pour atteindre un maximum local à 0, auquel cas elle diminue lentement au début, puis cesse de diminuer vers 1, puis continue de diminuer pour atteindre un minimum à 3, puis augmente rapidement.$

7) Trouvez l'approximation linéaire$L(x)$ à$y=x^2+\tan(πx)$ proximité$x=\frac{1}{4}.$

Réponse: $L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)\left(x−\frac{1}{4}\right)$

8) Trouvez la différence entre$y=x^2−5x−6$ et évaluez$x=2$ avec$dx=0.1.$

Déterminez les points critiques et les extrêmes locaux et absolus des fonctions suivantes sur l'intervalle donné.

9)$f(x)=x+\sin^2(x)$ terminé$[0,π]$

Réponse: Point critique : Minimum$x=\frac{3π}{4},$
absolu :$0$ quand Maximum$x=0,$
absolu :$π$ quand$x=π$

Solution :

10)$f(x)=3x^4−4x^3−12x^2+6$ plus$[−3,3]$

Déterminez les intervalles sur lesquels les fonctions suivantes sont croissantes, décroissantes, concaves vers le haut et concaves vers le bas.

11)$x(t)=3t^4−8t^3−18t^2$

Réponse: Croissant :$(−1,0)∪(3,∞),$
décroissant :$(−∞,−1)∪(0,3),$
concave vers le haut :$\left(−∞,\frac{1}{3}\left(2−\sqrt{13}\right)\right)∪\left(\frac{1}{3}\left(2+\sqrt{13}\right),∞\right)$,
concave vers le bas :$\left(\frac{1}{3}\left(2−\sqrt{13}\right),\frac{1}{3}\left(2+\sqrt{13}\right)\right)$

(12)$y=x+\sin(πx)$

13)$g(x)=x−\sqrt{x}$

Réponse: Croissant :$\left(\frac{1}{4},∞\right),$
décroissant :$\left(0,\frac{1}{4}\right)$
concave vers le haut :$(0,∞),$
concave vers le bas : nulle part

(14)$f(θ)=\sin(3θ)$

Évaluez les limites suivantes.

(15)$\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Réponse: $3$

16)$\displaystyle \lim_{x→∞}\cos\left(\frac{1}{x}\right)$

17)$\displaystyle \lim_{x→1}\frac{x−1}{\sin(πx)}$

Réponse: $−\frac{1}{π}$

18)$\displaystyle \lim_{x→∞}(3x)^{1/x}$

Utilisez la méthode de Newton pour trouver les deux premières itérations, en fonction du point de départ.

19)$y=x^3+1,\quad x_0=0.5$

Réponse: $x_1=−1,\; x_2=−1$

(20)$\dfrac{1}{x+1}=\dfrac{1}{2}, \quad x_0=0$

Trouvez les antidérivés$F(x)$ des fonctions suivantes.

(21)$g(x)=\sqrt{x}−\dfrac{1}{x^2}$

Réponse: $F(x)=\dfrac{2x^{3/2}}{3}+\dfrac{1}{x}+C$

(22)$f(x)=2x+6\cos x,\quad F(π)=π^2+2$

Représentez les fonctions suivantes à la main. Veillez à étiqueter les points d'inflexion, les points critiques, les zéros et les asymptotes.

23)$y=\dfrac{1}{x(x+1)^2}$

Réponse

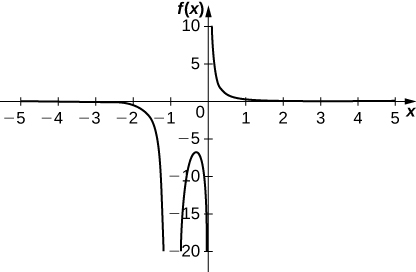
$Ce graphique présente des asymptotes verticales à x = 0 et x = −1. La première partie de la fonction se trouve dans le troisième quadrant avec une asymptote horizontale à y = 0. La fonction diminue rapidement de la proximité (−5, 0) à la proximité de l'asymptote verticale (−1, ∞). De l'autre côté de l'asymptote, la fonction est approximativement en forme de U et pointée vers le bas dans le troisième quadrant entre x = −1 et x = 0, le maximum étant proche (−0,4, −6). De l'autre côté de l'asympotote x = 0, la fonction diminue à partir de son asymptote verticale proche de (0, ∞) et pour s'approcher de l'asymptote horizontale y = 0.$

Points d'inflexion : aucun ; Points
critiques :$x=−\frac{1}{3}$ ;
Zéros : aucun ; Asymptotes
verticales :$x=−1, \; x=0$ ; Asymptote
horizontale :$y=0$

(24)$y=x−\sqrt{4−x^2}$

25) Une voiture est compactée pour former un solide rectangulaire. Le volume diminue à un rythme de$2\, \text{m}^3/\text{sec}$. La longueur et la largeur du compacteur sont carrées, mais la hauteur n'est pas la même que la longueur et la largeur. Si les parois de longueur et de largeur se rapprochent l'une de l'autre à une vitesse de$0.25$ m/sec, déterminez la vitesse à laquelle la hauteur change lorsque la longueur et la largeur sont$2$ m et que la hauteur est$1.5$ m.

Réponse: La hauteur diminue à une vitesse de$0.125$ m/sec

26) Une fusée est lancée dans l'espace ; son énergie cinétique est donnée par$K(t)=\frac{1}{2}m(t)v(t)^2$, où$K$ est l'énergie cinétique en joules,$m$ la masse de la fusée en kilogrammes et$v$ la vitesse de la fusée en mètres/seconde. Supposons que la vitesse augmente à une vitesse de$15 \,\text{m/sec}^2$ et que la masse diminue à une vitesse de$10$ kg/sec en raison de la combustion du carburant. À quelle vitesse l'énergie cinétique de la fusée change-t-elle lorsque la masse est de$2000$ kg et que la vitesse est de$5000$ m/sec ? Donnez votre réponse en méga-joules (MJ), ce qui équivaut à$10^6$ J.

27) Le célèbre problème de maximisation des angles du Regiomontanus a été proposé au cours du$15^\text{th}$ siècle. Un tableau est accroché à un mur, le bas du tableau étant à une distance de$a$ pieds au-dessus du niveau des yeux et les$b$ pieds supérieurs au-dessus du niveau des yeux. À quelle distance$x$ (en pieds) du mur le spectateur doit-il se tenir pour maximiser l'angle sous-tendu par la peinture$θ$ ?

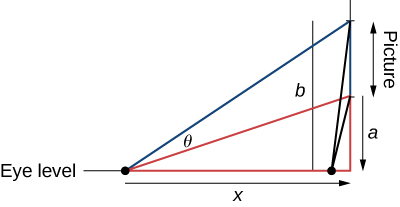
$Un point est marqué au niveau des yeux, et à partir de ce point, un triangle droit est formé avec une longueur de côté adjacente x et une longueur de côté opposé a, qui est la longueur entre le bas de l'image et le niveau de l'œil. Un second triangle droit est formé à partir du point marqué au niveau des yeux, le côté adjacent étant x et l'autre côté étant la longueur b, qui est la hauteur de l'image. L'angle entre les deux hypoténus est noté θ.$

Réponse: $x=\sqrt{ab}$pieds

28) Une compagnie aérienne vend des billets de Tokyo à Détroit pour$$1200.$ Il y a des$500$ places disponibles et un vol typique réserve des$350$ places. Pour chaque$$10$ baisse de prix, la compagnie aérienne constate la vente de cinq sièges supplémentaires. Quel doit être le tarif pour maximiser les profits ? Combien de passagers se trouveraient à bord ?