4.9 : Méthode de Newton

Objectifs d'apprentissage

• Décrivez les étapes de la méthode de Newton.
• Expliquez ce que signifie un processus itératif.
• Reconnaissez quand la méthode de Newton ne fonctionne pas.
• Appliquez des processus itératifs à différentes situations.

Dans de nombreux domaines des mathématiques pures et appliquées, nous souhaitons trouver des solutions à une équation de la forme. Cependant,\(f(x)=0.\) pour la plupart des fonctions, il est difficile, voire impossible, de calculer leurs zéros de manière explicite. Dans cette section, nous examinons une technique qui fournit un moyen très efficace d'approximer les zéros des fonctions. Cette technique utilise des approximations de lignes tangentes et est à l'origine de la méthode souvent utilisée par les calculateurs et les ordinateurs pour trouver des zéros.

Décrire la méthode de Newton

Considérez la tâche de trouver les solutions de\(f(x)=0.\) Si\(f\) est le polynôme du premier degré\(f(x)=ax+b\), alors la solution de\(f(x)=0\) est donnée par la formule\(x=−\frac{b}{a}\). Si\(f\) est le polynôme du second degré\(f(x)=ax^2+bx+c\), les solutions de\(f(x)=0\) peuvent être trouvées en utilisant la formule quadratique. Cependant, pour les polynômes de degré 3 ou plus, il\(f\) devient plus compliqué de trouver les racines de. Bien qu'il existe des formules pour les polynômes du troisième et du quatrième degré, elles sont assez compliquées. De plus, si f est un polynôme de degré 5 ou plus, on sait que de telles formules n'existent pas. Par exemple, considérez la fonction

\[f(x)=x^5+8x^4+4x^3−2x−7.\nonumber \]

Il n'existe aucune formule permettant de trouver les solutions à des difficultés\(f(x)=0.\) similaires pour les fonctions non polynomiales. Par exemple, considérez la tâche de trouver des solutions à\(\tan(x)−x=0.\) Aucune formule simple n'existe pour les solutions de cette équation. Dans de tels cas, nous pouvons utiliser la méthode de Newton pour approximer les racines.

La méthode de Newton utilise l'idée suivante pour approximer les solutions de\(f(x)=0.\) En esquissant un graphique de\(f\), nous pouvons estimer une racine de\(f(x)=0\). Appelons cela une estimation\(x_0\). Nous dessinons ensuite la tangente à\(f\) at\(x_0\). Si\(f′(x_0)≠0\), cette tangente coupe l'\(x\)axe -à un moment donné\((x_1,0)\). Passons maintenant\(x_1\) à la prochaine approximation de la racine réelle. En général,\(x_1\) est plus proche que\(x_0\) d'une racine réelle. Ensuite, nous dessinons la tangente à\(f\) at\(x_1\). Si\(f′(x_1)≠0\), cette tangente croise également l'\(x\)axe -, produisant une autre approximation,\(x_2\). Nous continuons ainsi, en dérivant une liste d'approximations :\(x_0,\, x_1,\, x_2,\, ….\) Généralement, les nombres\(x_0,\, x_1,\, x_2,\, …\) se rapprochent rapidement d'une racine réelle\(x^*\), comme le montre la figure suivante.

Figure : Les\(\PageIndex{1}\) approximations se rapprochent\(x_0,\, x_1,\, x_2,\, … \) de la racine réelle.\(x^*\) Les approximations sont dérivées en examinant les lignes tangentes au graphique de\(f\).

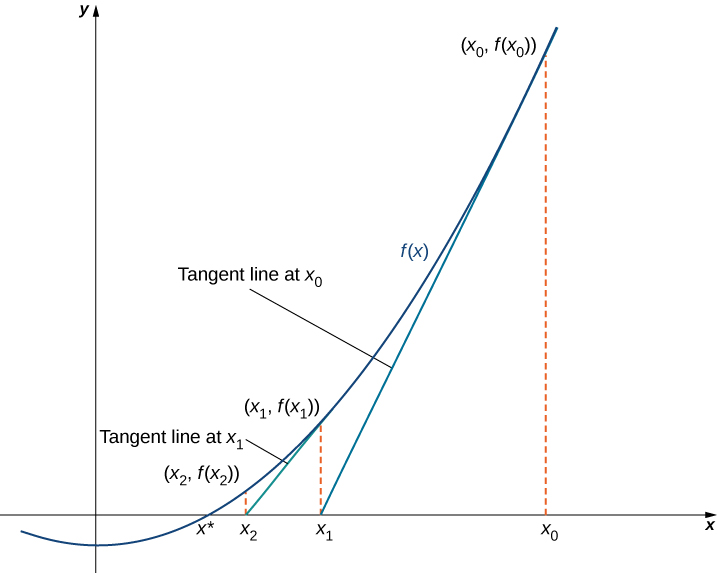
Voyons maintenant comment calculer les approximations.\(x_0,\, x_1,\, x_2,\, ….\) Si\(x_0\) est notre première approximation, l'approximation\(x_1\) est définie en laissant\((x_1,0)\) être l'\(x\)intersection de la tangente à\(f\) at\(x_0\). L'équation de cette tangente est donnée par

\[y=f(x_0)+f′(x_0)(x−x_0). \nonumber \]

Par conséquent,\(x_1\) doit satisfaire

\[f(x_0)+f′(x_0)(x_1−x_0)=0.\nonumber \]

En résolvant cette équation pour\(x_1\), nous concluons que

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}.\nonumber \]

De même, le point\((x_2,0)\) est l'\(x\)intersection de la tangente à\(f\) at\(x_1\). Par conséquent,\(x_2\) satisfait à l'équation

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}.\nonumber \]

En général, pour\(n>0,x_n\) satisfaire

\[x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}.\label{Newton} \]

Ensuite, nous verrons comment utiliser cette technique pour approximer la racine du polynôme.\(f(x)=x^3−3x+1.\)

Exemple\(\PageIndex{1}\): Finding a Root of a Polynomial

Utilisez la méthode de Newton pour approximer une racine de\(f(x)=x^3−3x+1\) dans l'intervalle\([1,2]\). Laisse\(x_0=2\) et trouve\(x_1,\, x_2, \,x_3, \,x_4,\) et\(x_5\).

Solution

Sur la figure\(\PageIndex{2}\), nous voyons qu'il\(f\) y a une racine sur l'intervalle\([1,2]\). \(x_0=2\)Cela semble donc être une première approximation raisonnable. Pour trouver l'approximation suivante, nous utilisons l'équation \ ref {Newton}. Puisque\(f(x)=x^3−3x+1\), le dérivé est\(f′(x)=3x^2−3\). En utilisant l'équation \ ref {Newton} avec\(n=1\) (et une calculatrice qui affiche des\(10\) chiffres), nous obtenons

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}=2−\frac{f(2)}{f'(2)}=2−\frac{3}{9}≈1.666666667.\nonumber \]

Pour trouver l'approximation suivante\(x_2\), nous utilisons l'équation \ ref {Newton} avec\(n=2\) et la valeur de\(x_1\) stockée sur la calculatrice. Nous constatons que

\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}≈1.548611111.\nonumber \]

En continuant ainsi, nous obtenons les résultats suivants :

• \(x_1≈1.666666667\)
• \(x_2≈1.548611111\)
• \(x_3≈1.532390162\)
• \(x_4≈1.532088989\)
• \(x_5≈1.532088886\)
• \(x_6≈1.532088886.\)

Nous notons que nous avons obtenu la même valeur pour\(x_5\) et\(x_6\). Par conséquent, toute application ultérieure de la méthode de Newton donnera très probablement la même valeur pour\(x_n\).

Figure\(\PageIndex{2}\) : La fonction\(f(x)=x^3−3x+1\) possède une racine au cours de l'intervalle\([1,2].\)

Exercice\(\PageIndex{1}\)

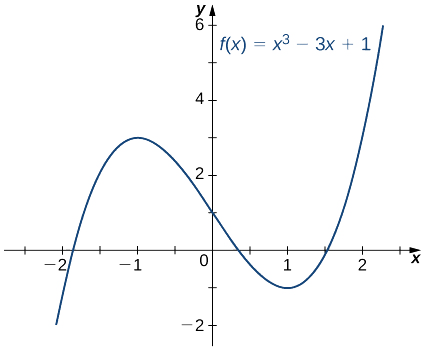
\(x_0=0\)Utilisons la méthode de Newton pour approximer la racine de l'\(f(x)=x^3−3x+1\)intervalle\([0,1]\) en calculant\(x_1\) et\(x_2\).

Allusion

Utilisez l'équation \ ref {Newton}.

Réponse

\(x_1≈0.33333333\)
\(x_2≈0.347222222\)

La méthode de Newton peut également être utilisée pour approximer les racines carrées. Nous montrons ici comment approximer\(\sqrt{2}\). Cette méthode peut être modifiée pour approximer la racine carrée de tout nombre positif.

Exemple\(\PageIndex{2}\): Finding a Square Root

Utilisez la méthode de Newton pour obtenir une approximation\(\sqrt{2}\) (Figure\(\PageIndex{3}\)). Laissez\(f(x)=x^2−2\)\(x_0=2\), laissez et calculez\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). (Nous remarquons\(f(x)=x^2−2\) que puisque la valeur initiale est nulle\(\sqrt{2}\),\(x_0=2\) il est raisonnable de faire un choix approximatif\(\sqrt{2}\)).

Figure\(\PageIndex{3}\) : Nous pouvons utiliser la méthode de Newton pour trouver\(\sqrt{2}\).

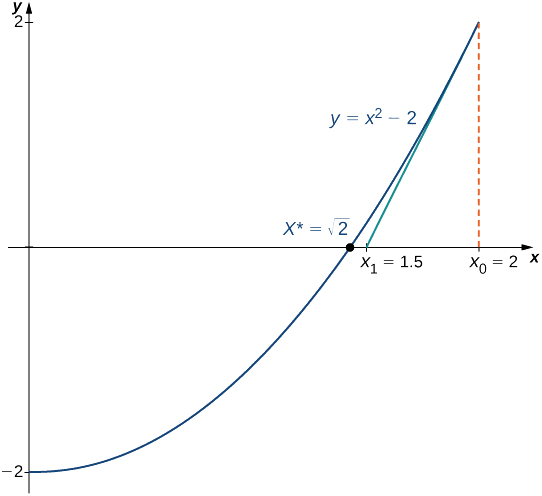
Solution

Pour\(f(x)=x^2−2,\; f′(x)=2x.\) From Equation \ ref {Newton}, nous savons que

\ [\ begin {align*} x_n&=x_ {n−1} − \ frac {f (x_ {n−1})} {f' (x_ {n−1})} \ \ [4 points]
&=x_ {n−1} − \ frac {x^2_ {n−1} −2} {2x_ {n−1}} \ \ [4pt]
&= \ frac {1} {2} x_ {n−1} + \ frac {1} {x_ {n−1}} \ \ [4 points]
&= \ frac {1} {2} \ gauche (x_ {n−1} + \ frac {2} {x_ {n−1}} \ droite). \ end {align*} \ nonumber \]

Par conséquent,

\(x_1=\frac{1}{2}\left(x_0+\frac{2}{x_0}\right)=\frac{1}{2}\left(2+\frac{2}{2}\right)=1.5\)

\(x_2=\frac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\frac{1}{2}\left(1.5+\frac{2}{1.5}\right)≈1.416666667.\)

En continuant ainsi, nous constatons que

\(x_1=1.5\)

\(x_2≈1.416666667\)

\(x_3≈1.414215686\)

\(x_4≈1.414213562\)

\(x_5≈1.414213562.\)

Comme nous avons obtenu la même valeur pour\(x_4\) et\(x_5\), il est peu probable que cette valeur\(x_n\) change lors d'une application ultérieure de la méthode de Newton. Nous concluons que\(\sqrt{2}≈1.414213562.\)

Exercice\(\PageIndex{2}\)

Utilisez la méthode de Newton pour approximer\(\sqrt{3}\) en laissant\(f(x)=x^2−3\) et\(x_0=3\). Trouvez\(x_1\) et\(x_2\).

Allusion

Pour\(f(x)=x^2−3\), l'équation \ ref {Newton} se réduit à\(x_n=\frac{x_{n−1}}{2}+\frac{3}{2x_{n−1}}\).

Réponse

\(x_1=2\)
\(x_2=1.75\)

Lorsque vous utilisez la méthode de Newton, chaque approximation après l'estimation initiale est définie en fonction de l'approximation précédente en utilisant la même formule. En particulier, en définissant la fonction\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\), nous pouvons réécrire l'équation \ ref {Newton} sous la forme\(x_n=F(x_{n−1})\). Ce type de processus, dans lequel chacun\(x_n\) est défini en termes de\(x_{n−1}\) répétition de la même fonction, est un exemple de processus itératif. Nous examinerons prochainement d'autres processus itératifs. Tout d'abord, examinons les raisons pour lesquelles la méthode de Newton pourrait ne pas trouver de racine.

Les échecs de la méthode de Newton

En général, la méthode de Newton est utilisée pour trouver des racines assez rapidement. Cependant, les choses peuvent mal tourner. Parmi les raisons pour lesquelles la méthode de Newton peut échouer, citons les suivantes :

1. À l'une des approximations\(x_n\), la dérivée\(f′\) est nulle à\(x_n\), mais\(f(x_n)≠0\). Par conséquent, la tangente de\(f\) at\(x_n\) n'intersecte pas l'\(x\)axe. Nous ne pouvons donc pas poursuivre le processus itératif.
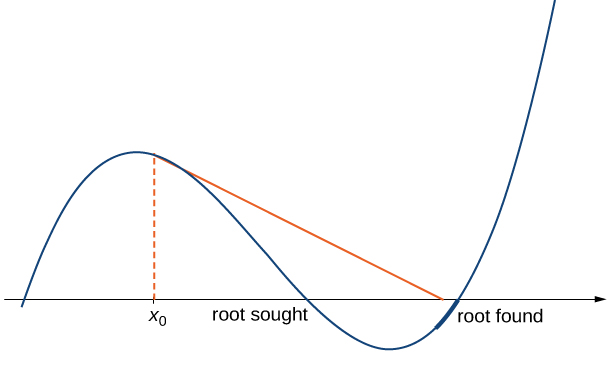
2. Les approximations\(x_0,\, x_1,\, x_2,\, …\) peuvent s'approcher d'une racine différente. Si la fonction\(f\) possède plusieurs racines, il est possible que nos approximations ne se rapprochent pas de celle que nous recherchons, mais s'approchent d'une racine différente (voir Figure\(\PageIndex{4}\)). Cet événement se produit le plus souvent lorsque nous ne choisissons pas l'approximation suffisamment\(x_0\) proche de la racine souhaitée.
3. Les approximations peuvent ne pas s'approcher complètement d'une racine. Dans Exemple\(\PageIndex{3}\), nous fournissons un exemple de fonction et une estimation initiale de\(x_0\) telle sorte que les approximations successives ne s'approchent jamais d'une racine car les approximations successives continuent d'alterner entre deux valeurs.

Figure\(\PageIndex{4}\) : Si l'estimation initiale\(x_0\) est trop éloignée de la racine recherchée, cela peut conduire à des approximations se rapprochant d'une racine différente.

Exemple\(\PageIndex{3}\): When Newton’s Method Fails

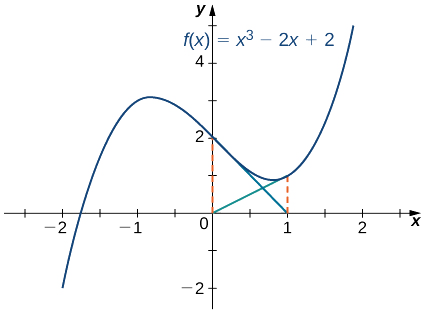
Réfléchissez à la fonction\(f(x)=x^3−2x+2\). Laissez\(x_0=0\). Montrez que la séquence\(x_1,\, x_2,\, …\) ne parvient pas à s'approcher de la racine de\(f\).

Solution

Car\(f(x)=x^3−2x+2,\) le dérivé est\(f′(x)=3x^2−2\) .Par conséquent,

\[x_1=x_0−\frac{f(x_0)}{f′(x_0)}=0−\frac{f(0)}{f′(0)}=−\frac{2}{−2}=1. \nonumber \]

À l'étape suivante,

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}=1−\frac{f(1)}{f′(1)}=1−\frac{1}{1}=0. \nonumber \]

Par conséquent, les nombres\(x_0,\, x_1,\, x_2,\, …\) continuent de rebondir entre les deux\(0\)\(1\) et ne se rapprochent jamais de la racine,\(f\) dont la racine se trouve au-dessus de l'intervalle\([−2,−1]\) (Figure\(\PageIndex{5}\)). Heureusement, si nous choisissons une approximation initiale\(x_0\) plus proche de la racine réelle, nous pouvons éviter cette situation.

Figure\(\PageIndex{5}\) : Les approximations continuent d'alterner entre\(0\)\(1\) et ne s'approchent jamais de la racine de\(f\).

Exercice\(\PageIndex{3}\)

Pour\(f(x)=x^3−2x+2,\) louer\(x_0=−1.5\) et trouver\(x_1\) et\(x_2\).

Allusion

Utilisez l'équation \ ref {Newton}.

Réponse

\(x_1≈−1.842105263\)
\(x_2≈−1.772826920\)

Dans l'exemple\(\PageIndex{3}\), nous voyons que la méthode de Newton ne fonctionne pas toujours. Cependant, lorsqu'elle fonctionne, la séquence d'approximations se rapproche très rapidement de la racine. Des discussions sur la rapidité avec laquelle la séquence d'approximations s'approche d'une racine trouvée à l'aide de la méthode de Newton sont incluses dans des textes sur l'analyse numérique.

Autres processus itératifs

Comme mentionné précédemment, la méthode de Newton est un type de processus itératif. Nous examinons maintenant un exemple d'un autre type de processus itératif.

Prenons l'exemple d'une fonction\(F\) et d'un numéro initial\(x_0\). Définissez les nombres suivants à l'\(x_n\)aide de la formule\(x_n=F(x_{n−1})\). Ce processus est un processus itératif qui crée une liste de nombres.\(x_0,\, x_1,\, x_2,\, …,\, x_n,\, ….\) Cette liste de nombres peut s'approcher d'un nombre fini au\(x^*\)\(n\) fur et à mesure qu'elle s'agrandit, ou non. Dans Exemple\(\PageIndex{4}\), nous voyons un exemple de fonction\(F\) et une estimation initiale de\(x_0\) telle sorte que la liste de nombres résultante se rapproche d'une valeur finie.

Exemple\(\PageIndex{4}\): Finding a Limit for an Iterative Process

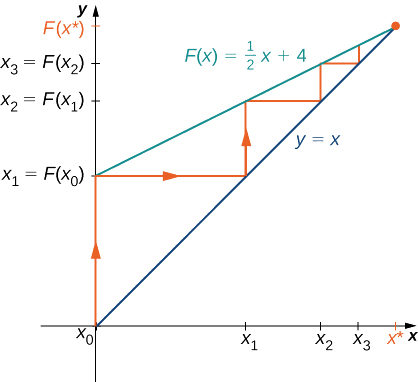
Laisse\(F(x)=\frac{1}{2}x+4\) et laisse\(x_0=0\). Pour tous\(n≥1\), laissez\(x_n=F(x_{n−1})\). Trouvez les valeurs\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Faites une conjecture sur ce qu'il advient de cette liste de nombres\(x_1,\, x_2,\, x_3,\, …,\, x_n,\, …\) en tant que\(n→∞\). Si la liste de nombres se\(x_1,\, x_2,\, x_3,\, …\) rapproche d'un nombre fini\(x^*\)\(x^*=F(x^*)\), alors\(x^*\) satisfait et\(x^*\) est appelée point fixe de\(F\).

Solution

Si\(x_0=0\), alors

• \(x_1=\frac{1}{2}(0)+4=4\)
• \(x_2=\frac{1}{2}(4)+4=6\)
• \(x_3=\frac{1}{2}(6)+4=7\)
• \(x_4=\frac{1}{2}(7)+4=7.5\)
• \(x_5=\frac{1}{2}(7.5)+4=7.75\)
• \(x_6=\frac{1}{2}(7.75)+4=7.875\)
• \(x_7=\frac{1}{2}(7.875)+4=7.9375\)
• \(x_8=\frac{1}{2}(7.9375)+4=7.96875\)
• \(x _9=\frac{1}{2}(7.96875)+4=7.984375.\)

À partir de cette liste, nous supposons que les valeurs se\(x_n\) rapprochent\(8\).

La figure\(\PageIndex{6}\) fournit un argument graphique indiquant que les valeurs se rapprochent\(8\) de\(n→∞\). En commençant par le point\((x_0,x_0)\), nous tracons une ligne verticale jusqu'au point\((x_0,F(x_0))\). Le prochain numéro de notre liste est\(x_1=F(x_0)\). Nous utilisons\(x_1\) pour calculer\(x_2\). Par conséquent, nous dessinons une ligne horizontale reliant\((x_0,x_1)\)\((x_1,x_1)\) le point de la ligne\(y=x\), puis une ligne verticale reliant\((x_1,x_1)\) le point\((x_1,F(x_1))\). La sortie\(F(x_1)\) devient\(x_2\). En continuant ainsi, nous pourrions créer un nombre infini de segments de ligne. Ces segments de ligne sont piégés entre les lignes\(F(x)=\frac{x}{2}+4\) et\(y=x\). Les segments de droite se rapprochent du point d'intersection de ces deux lignes, qui se produit lorsque\(x=F(x)\). En résolvant l'équation,\(x=\frac{x}{2}+4,\) nous concluons qu'ils se croisent\(x=8\). Par conséquent, nos preuves graphiques sont en accord avec nos preuves numériques selon lesquelles la liste des nombres se\(x_0,\, x_1,\, x_2,\, …\) rapproche\(x^*=8\) de\(n→∞\).

Figure\(\PageIndex{6}\) : Ce processus itératif se rapproche de la valeur\(x^*=8.\)

Exercice\(\PageIndex{4}\)

Réfléchissez à la fonction\(F(x)=\frac{1}{3}x+6\). Laisse\(x_0=0\) et laisse\(x_n=F(x_{n−1})\)\(n≥2\). Trouve\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Faites une conjecture sur ce qu'il advient de la liste des nombres\(x_1,\, x_2,\, x_3,\, …\, x_n,\, … \) en tant que\(n→∞.\)

Allusion

Considérez le point où les lignes\(y=x\) se\(y=F(x)\) croisent.

Réponse

\(x_1=6,\;x_2=8,\;x_3=\frac{26}{3},\;x_4=\frac{80}{9},\;x_5=\frac{242}{27};\;x^*=9\)

Processus itératifs et chaos

Les processus itératifs peuvent donner lieu à des comportements très intéressants. Dans cette section, nous avons vu plusieurs exemples de processus itératifs qui convergent vers un point fixe. Nous avons également vu dans\(\PageIndex{3}\) Example que le processus itératif rebondissait entre deux valeurs. Nous appelons ce type de comportement un double cycle. Les processus itératifs peuvent converger en cycles avec différentes périodicités, tels que 2 cycles, 4 cycles (où le processus itératif répète une séquence de quatre valeurs), 8 cycles, etc.

Certains processus itératifs engendrent ce que les mathématiciens appellent le chaos. Dans ce cas, le processus itératif passe d'une valeur à l'autre de manière apparemment aléatoire et ne converge jamais ni ne s'installe dans un cycle. Bien que l'exploration complète du chaos dépasse le cadre de ce texte, nous examinons dans ce projet l'une des principales propriétés d'un processus itératif chaotique : la dépendance sensible aux conditions initiales. Cette propriété fait référence au concept selon lequel de petites modifications des conditions initiales peuvent générer un comportement radicalement différent dans le processus itératif.

L'exemple de chaos le plus connu est probablement l'ensemble de Mandelbrot (voir Figure\(\PageIndex{7}\)), nommé d'après Benoit Mandelbrot (1924-2010), qui a étudié ses propriétés et contribué à vulgariser le domaine de la théorie du chaos. L'ensemble de Mandelbrot est généralement généré par ordinateur et présente des détails fascinants sur l'agrandissement, y compris l'autoréplication de l'ensemble. Plusieurs versions colorisées de l'ensemble ont été présentées dans des musées et peuvent être consultées en ligne et dans des livres populaires sur le sujet.

Figure\(\PageIndex{7}\) : L'ensemble de Mandelbrot est un exemple bien connu d'ensemble de points générés par le comportement chaotique itératif d'une fonction relativement simple.

Dans ce projet, nous utilisons la carte logistique

\[f(x)=rx(1−x) \nonumber \]

où\(x∈[0,1]\) et\(r>0\)

comme fonction de notre processus itératif. La carte logistique est une fonction d'une simplicité trompeuse ; mais, selon la valeur de\(r\), le processus itératif qui en résulte présente un comportement très intéressant. Cela peut mener à des points fixes, à des cycles et même au chaos.

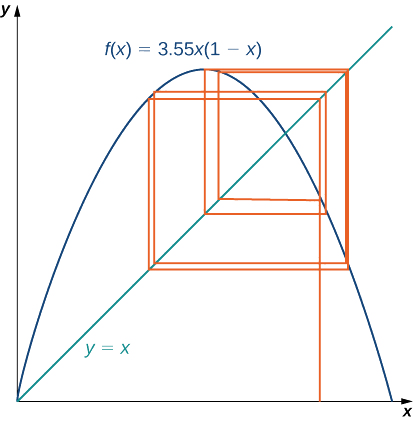
Pour visualiser le comportement à long terme du processus itératif associé à la carte logistique, nous utiliserons un outil appelé diagramme en toile d'araignée. Comme nous l'avons fait pour le processus itératif que nous avons examiné plus tôt dans cette section, nous tracons d'abord une ligne verticale d'un point\((x_0,0)\) à un point\((x_0,f(x_0))=(x_0,x_1)\). Nous tracons ensuite une ligne horizontale entre ce point et le point\((x_1,f(x_1))=(x_1,x_2)\),\((x_1,x_1),\) puis une ligne verticale jusqu'à ce que le comportement à long terme du système devienne évident et nous poursuivons le processus. La figure\(\PageIndex{8}\) montre le comportement à long terme de la carte logistique lorsque\(r=3.55\) et\(x_0=0.2\). (Les premières\(100\) itérations ne sont pas tracées.) Le comportement à long terme de ce processus itératif est un\(8\) cycle.

Figure\(\PageIndex{8}\) : Un diagramme en toile d'araignée pour\(f(x)=3.55x(1−x)\) est présenté ici. La séquence de valeurs donne lieu à un cycle de 8.

1. Laissez\(r=0.5\) et choisissez\(x_0=0.2\). À la main ou à l'aide d'un ordinateur, calculez les premières\(10\) valeurs de la séquence. La séquence semble-t-elle converger ? Dans l'affirmative, à quelle valeur ? Cela entraîne-t-il un cycle ? Si c'est le cas, quel type de cycle (par exemple,\(2\) −cycle,\(4\) −cycle.) ?
2. Que se passe-t-il quand\(r=2\) ?
3. Pour\(r=3.2\) et\(r=3.5\), calculez les premières valeurs de\(100\) séquence. Générez un diagramme en toile d'araignée pour chaque processus itératif. (Plusieurs applets gratuits sont disponibles en ligne pour générer des diagrammes en toile d'araignée pour la carte logistique.) Quel est le comportement à long terme dans chacun de ces cas ?
4. Maintenant,\(r=4.\) calculons les premières valeurs de\(100\) séquence et générez un diagramme en toile d'araignée. Quel est le comportement à long terme dans ce cas ?
5. Répétez le processus pour\(r=4,\) mais laissez\(x_0=0.201.\) Comment ce comportement se compare-t-il au comportement de\(x_0=0.2\) ?

Concepts clés

• La méthode de Newton se rapproche des racines de\(f(x)=0\) en commençant par une approximation initiale\(x_0\), puis utilise des lignes tangentes au graphe de\(f\) pour créer une séquence d'approximations\(x_1,\, x_2,\, x_3,\, ….\)
• En général, la méthode de Newton est une méthode efficace pour trouver une racine particulière. Dans certains cas, la méthode de Newton ne fonctionne pas parce que la liste des nombres\(x_0,\, x_1,\, x_2,\, …\) ne s'approche pas d'une valeur finie ou s'approche d'une valeur autre que la racine recherchée.
• Tout processus dans lequel une liste de nombres\(x_0,\, x_1,\, x_2,\, …\) est générée en définissant un nombre initial\(x_0\) et en définissant les nombres suivants par l'équation\(x_n=F(x_{n−1})\) d'une fonction\(F\) est un processus itératif. La méthode de Newton est un exemple de processus itératif, où la fonction\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\) d'une fonction donnée\(f\).

Lexique

processus itératif

processus dans lequel une liste de nombres\(x_0,x_1,x_2,x_3…\) est générée en commençant par un nombre\(x_0\) et en définissant\(x_n=F(x_{n−1})\) pour\(n≥1\)

La méthode de Newton

méthode d'approximation des racines de\(f(x)=0;\) l'utilisation d'une estimation initiale\(x_0\) ; chaque approximation suivante est définie par l'équation\(x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}\)