4.5 : Les dérivées et la forme d'un graphe
- Page ID
- 197593
- Expliquez comment le signe de la dérivée première affecte la forme du graphe d'une fonction.
- Indiquez le premier test dérivé pour les points critiques.
- Utilisez la concavité et les points d'inflexion pour expliquer comment le signe de la dérivée seconde affecte la forme du graphe d'une fonction.
- Expliquer le test de concavité d'une fonction sur un intervalle ouvert.
- Expliquez la relation entre une fonction et ses dérivées première et seconde.
- Indiquez le deuxième test dérivé pour les extrêmes locaux.
Plus tôt dans ce chapitre, nous avons indiqué que si une fonction\(f\) possède un extremum local en un point\(c\), alors\(c\) il doit s'agir d'un point critique de\(f\). Cependant, il n'est pas garanti qu'une fonction possède un extremum local à un point critique. Par exemple,\(f(x)=x^3\) possède un point critique à\(x=0\) puisque\(f'(x)=3x^2\) vaut zéro à\(x=0\), mais\(f\) n'a pas d'extremum local à\(x=0\). À l'aide des résultats de la section précédente, nous sommes maintenant en mesure de déterminer si un point critique d'une fonction correspond réellement à une valeur extrême locale. Dans cette section, nous verrons également comment la dérivée seconde fournit des informations sur la forme d'un graphe en décrivant si le graphe d'une fonction est incurvé vers le haut ou vers le bas.
Le premier test dérivé
Le corollaire\(3\) du théorème de la valeur moyenne a montré que si la dérivée d'une fonction est positive sur un intervalle\(I\), alors la fonction augmente\(I\). En revanche, si la dérivée de la fonction est négative sur un intervalle\(I\), alors la fonction décroît\(I\) comme indiqué dans la figure suivante.
Une fonction continue\(f\) a un maximum local au point\(c\) si et seulement si elle\(f\) passe d'une valeur croissante à une valeur décroissante au point\(c\). De même,\(f\) a un minimum local à if et\(c\) only if\(f\) bascule d'une valeur décroissante à une valeur croissante à\(c\). S'il s'\(f\)agit d'une fonction continue sur un intervalle\(I\) contenant\(c\) et dérivable sur\(I\), sauf éventuellement à\(c\), la seule façon de\(f\) passer de l'augmentation à la diminution (ou vice versa) au point\(c\) est de\(f'\) changer de signe comme \(x\)augmente jusqu'à\(c\). \(f\)Il est différenciable à\(c\), la seule façon de\(f'\) changer de signe à mesure que l'on\(x\) augmente\(c\) est si\(f'(c)=0\). Par conséquent, pour une fonction\(f\) continue sur un intervalle\(I\) contenant\(c\) et dérivable sur\(I\), sauf éventuellement à\(c\), la seule façon\(f\) de passer d'une fonction croissante à une valeur décroissante (ou vice versa) est si\(f'(c)=0\) ou n'\(f'(c)\)est pas définie. Par conséquent, pour localiser les extrêmes locaux d'une fonction\(f\), nous recherchons des points\(c\) dans le domaine de\(f\) tels extrêmes\(f'(c)=0\) ou\(f'(c)\) non définis. Rappelez-vous que ces points sont appelés points critiques de\(f\).
Notez qu'\(f\)il n'est pas nécessaire d'avoir un extrema local à un point critique. Les points critiques ne peuvent être considérés que pour les extrêmes locaux. Dans la figure\(\PageIndex{2}\), nous montrons que si une fonction continue\(f\) possède un extremum local, elle doit apparaître à un point critique, mais qu'une fonction peut ne pas avoir d'extremum local à un point critique. Nous montrons qu'il y\(f\) a un extremum local à un point critique, alors le signe des\(f'\) commutateurs\(x\) augmente à travers ce point.
À l'aide de la figure\(\PageIndex{2}\), nous résumons les principaux résultats concernant les extrêmes locaux.
- Si une fonction continue\(f\) possède un extremum local, il doit se produire à un point critique\(c\).
- La fonction possède un extremum local au point critique\(c\) si et seulement si la dérivée\(f'\) change de signe d'\(x\)augmentation\(c\).
- Par conséquent, pour vérifier si une fonction possède un extremum local à un point critique\(c\), nous devons déterminer le signe de\(f'(x)\) à gauche et à droite de\(c\).
Ce résultat est connu sous le nom de premier test dérivé.
Supposons qu'\(f\)il s'agisse d'une fonction continue sur un intervalle\(I\) contenant un point critique\(c\). S'il\(f\) est différenciable\(I\), sauf éventuellement au point\(c\),\(f(c)\) répond alors à l'une des descriptions suivantes :
- Si le signe\(f'\) passe du signe positif\(x<c\) au moment négatif\(x>c\), alors\(f(c)\) est un maximum local de\(f\).
- Si le signe\(f'\) passe de négatif quand\(x<c\) à positif quand\(x>c\), alors\(f(c)\) est un minimum local de\(f\).
- S'il\(f'\) a le même signe pour\(x<c\) et\(x>c\), alors n'\(f(c)\)est ni un maximum local ni un minimum local de\(f\)
Voyons maintenant comment utiliser cette stratégie pour localiser tous les extrêmes locaux pour des fonctions particulières.
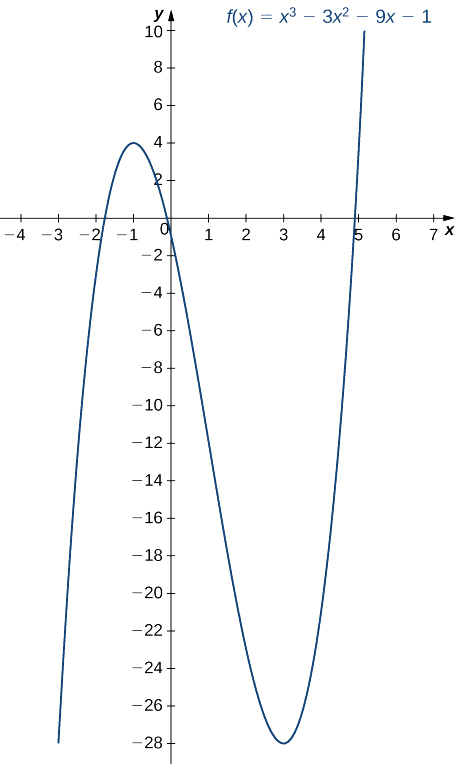
Utilisez le premier test dérivé pour trouver l'emplacement de tous les extrêmes locaux pour\(f(x)=x^3−3x^2−9x−1.\) Utiliser un utilitaire graphique pour confirmer vos résultats.
Solution
Étape 1. La dérivée est :\(f'(x)=3x^2−6x−9.\) Pour trouver les points critiques, nous devons trouver où\(f'(x)=0.\) Factoriser le polynôme, nous concluons que les points critiques doivent satisfaire
\[3(x^2−2x−3)=3(x−3)(x+1)=0. \nonumber \]
Par conséquent, les points critiques sont\(x=3,−1.\) Maintenant, divisez l'intervalle\((−∞,∞)\) en intervalles plus petits\((−∞,−1),(−1,3)\) et\((3,∞).\)
Étape 2. Comme il\(f'\) s'agit d'une fonction continue, pour déterminer le signe de\(f'(x)\) sur chaque sous-intervalle, il suffit de choisir un point sur chacun des intervalles\((−∞,−1),(−1,3)\)\((3,∞)\) et de déterminer le signe de\(f'\) en chacun de ces points. Par exemple, choisissons\(x=−2\)\(x=0\), et\(x=4\) comme points de test.
| Intervalle | Point d'essai | Panneau indiquant le\(f'(x)=3(x−3)(x+1)\) point de test | Conclusion |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =3 (x−3) (x+1) \) au point de test » style="vertical-align:middle ; « > (+) (−) (−) (−) =+ | \(f\)augmente. |
| \((−1,3)\) | \(x=0\) | \ (f' (x) =3 (x−3) (x+1) \) au point de test » style="vertical-align:middle ; « > (+) (−) (+) (+) =- | \(f\)est en baisse. |
| \((3,∞)\) | \(x=4\) | \ (f' (x) =3 (x−3) (x+1) \) au point de test » style="vertical-align:middle ; « > (+) (+) (+) (+) (+) =+ | \(f\)augmente. |
Étape 3. Puisque le signe\(f'\) passe du positif au négatif au fur et à mesure qu'il\(x\) augmente\(-1\),\(f\) a un maximum local à\(x=−1\). Puisque les\(f'\) signes passent du négatif au positif au fur et à mesure qu'ils\(x\) augmentent\(3\),\(f\) a un minimum local à\(x=3\). Ces résultats analytiques concordent avec le graphique suivant.
Utilisez le premier test dérivé pour localiser tous les extrêmes locaux pour\(f(x)=−x^3+\frac{3}{2}x^2+18x.\)
- Allusion
-
Trouvez tous les points critiques\(f\) et déterminez les signes\(f'(x)\) sur des intervalles particuliers déterminés par les points critiques.
- Réponse
-
\(f\)a un minimum local à\(−2\) et un maximum local à\(3\).
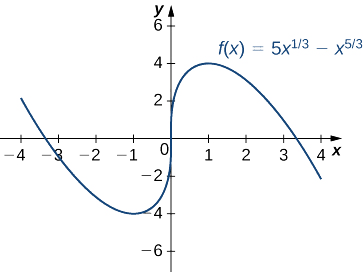
Utilisez le premier test dérivé pour trouver l'emplacement de tous les extrêmes locaux pour\(f(x)=5x^{1/3}−x^{5/3}.\) Utiliser un utilitaire graphique pour confirmer vos résultats.
Solution
Étape 1. Le dérivé est
\[f'(x)=\frac{5}{3}x^{−2/3}−\frac{5}{3}x^{2/3}=\frac{5}{3x^{2/3}}−\frac{5x^{2/3}}{3}=\frac{5−5x^{4/3}}{3x^{2/3}}=\frac{5(1−x^{4/3})}{3x^{2/3}}.\nonumber \]
La dérivée\(f'(x)=0\) lorsque\(1−x^{4/3}=0.\) Donc,\(f'(x)=0\) à\(x=±1\). La dérivée n'\(f'(x)\)est pas définie à\(x=0.\) Par conséquent, nous avons trois points critiques :\(x=0\),\(x=1\), et\(x=−1\). Par conséquent, divisez l'intervalle\((−∞,∞)\) en intervalles plus petits\((−∞,−1),\,(−1,0),\,(0,1)\), et\((1,∞)\).
Étape 2 : Comme elle\(f'\) est continue sur chaque sous-intervalle, il suffit de choisir un point de test\(x\) dans chacun des intervalles de l'étape 1 et de déterminer le signe de\(f'\) en chacun de ces points. Les points\(x=−2,\,x=−\frac{1}{2},\,x=\frac{1}{2}\) et\(x=2\) sont des points de test pour ces intervalles.
| Intervalle | Point d'essai | Panneau indiquant le\(f'(x)=\frac{5(1−x^{4/3})}{3x^{2/3}}\) point de test | Conclusion |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) = \ frac {5 (1−x^ {4/3})} {3x^ {2/3}} \) au point de test » style="vertical-align:middle ; « >\(\frac{(+)(−)}{+}=−\) | \(f\)est en baisse. |
| \((−1,0)\) | \(x=−\frac{1}{2}\) | \ (f' (x) = \ frac {5 (1−x^ {4/3})} {3x^ {2/3}} \) au point de test » style="vertical-align:middle ; « >\(\frac{(+)(+)}{+}=+\) | \(f\)augmente. |
| \((0,1)\) | \(x=\frac{1}{2}\) | \ (f' (x) = \ frac {5 (1−x^ {4/3})} {3x^ {2/3}} \) au point de test » style="vertical-align:middle ; « >\(\frac{(+)(+)}{+}=+\) | \(f\)augmente. |
| \((1,∞)\) | \(x=2\) | \ (f' (x) = \ frac {5 (1−x^ {4/3})} {3x^ {2/3}} \) au point de test » style="vertical-align:middle ; « >\(\frac{(+)(−)}{+}=−\) | \(f\)est en baisse. |
Étape 3 : Puisque\(f\) diminue au cours de l'intervalle\((−∞,−1)\) et augmente au cours de l'intervalle\((−1,0)\),\(f\) a un minimum local à\(x=−1\). Puisque\(f\) augmente au cours de l'intervalle\((−1,0)\) et de l'intervalle\((0,1)\),\(f\) n'a pas d'extremum local à\(x=0\). Puisque\(f\) augmente au cours de l'intervalle\((0,1)\) et diminue au cours de l'intervalle\((1,∞)\),\(f\) a un maximum local à\(x=1\). Les résultats analytiques concordent avec le graphique suivant.
Utilisez le premier test dérivé pour trouver tous les extrêmes locaux pour\(f(x)=\dfrac{3}{x−1}\).
- Allusion
-
Le seul point critique\(f\) est\(x=1.\)
- Réponse
-
\(f\)n'a pas d'extrêma local car\(f'\) ne change pas de signe à\(x=1\).
Concavité et points d'inflexion
Nous savons maintenant comment déterminer où une fonction augmente ou diminue. Cependant, il y a un autre problème à prendre en compte concernant la forme du graphe d'une fonction. Si le graphique est incurvé, courbe-t-il vers le haut ou vers le bas ? Cette notion s'appelle la concavité de la fonction.
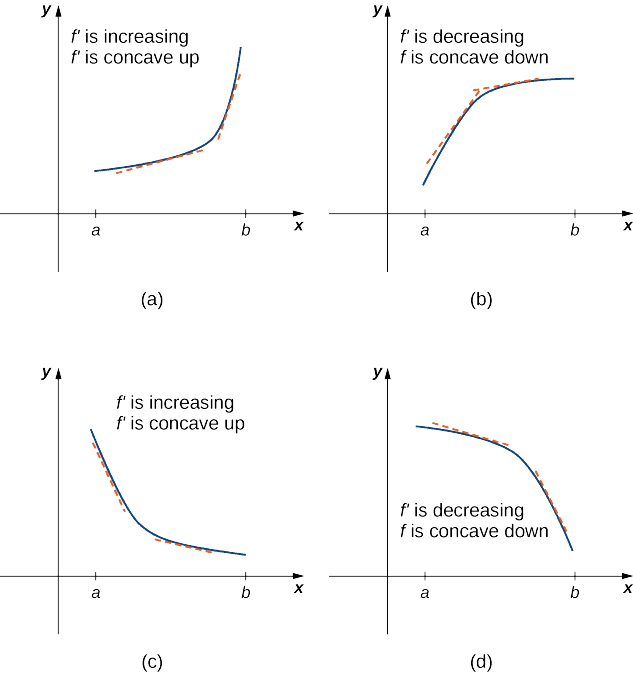
La figure\(\PageIndex{5a}\) montre une fonction\(f\) avec un graphique incurvé vers le haut. Au fur et à mesure qu'elle\(x\) augmente, la pente de la tangente augmente. Ainsi, puisque la dérivée augmente au fur et à mesure qu'elle\(x\) augmente,\(f'\) est une fonction croissante. Nous disons que cette fonction\(f\) est concave vers le haut. La figure\(\PageIndex{5b}\) montre une fonction\(f\) incurvée vers le bas. À mesure qu'elle\(x\) augmente, la pente de la tangente diminue. Puisque la dérivée diminue à mesure qu'elle\(x\) augmente,\(f'\) est une fonction décroissante. Nous disons que cette fonction\(f\) est concave vers le bas.
\(f\)Soit une fonction différentiable sur un intervalle ouvert\(I\). Si elle\(f'\) augmente\(I\), nous disons qu'elle\(f\) est concave vers le haut\(I\). Si elle\(f'\) est décroissante\(I\), nous disons qu'elle\(f\) est concave vers le bas\(I\).
En général, sans avoir le graphe d'une fonction\(f\), comment déterminer sa concavité ? Par définition, une fonction\(f\) est concave vers le haut si elle\(f'\) augmente. À partir de Corollary\(3\), nous savons que si\(f'\) c'est une fonction dérivable, alors augmente si\(f'\) c'est sa dérivée\(f''(x)>0\). Par conséquent, une fonction\(f\) qui est deux fois dérivable est concave vers le haut lorsque\(f''(x)>0\). De même, une fonction\(f\) est concave vers le bas si elle\(f'\) est décroissante. Nous savons qu'une fonction dérivable\(f'\) est décroissante si sa dérivée\(f''(x)<0\). Par conséquent, une fonction deux fois différenciable\(f\) est concave vers le bas quand\(f''(x)<0\). L'application de cette logique est connue sous le nom de test de concavité.
\(f\)Soit une fonction deux fois différenciable sur un intervalle\(I\).
- Si c'est\(f''(x)>0\) pour tout\(x∈I\), alors\(f\) est concave vers le haut\(I\)
- Si c'est\(f''(x)<0\) pour tout\(x∈I,\), alors\(f\) est concave vers le bas\(I\).
Nous concluons que nous pouvons déterminer la concavité d'une fonction\(f\) en examinant la dérivée seconde de\(f\). De plus, nous observons qu'une fonction\(f\) peut changer de concavité (Figure\(\PageIndex{6}\)). Cependant, une fonction continue ne peut changer de concavité qu'à un point\(x\) si celui-ci n'\(f''(x)\)est pas défini\(f''(x)=0\) ou non défini. Par conséquent, pour déterminer les intervalles où une fonction\(f\) est concave vers le haut et concave vers le bas, nous recherchons les valeurs\(x\) où\(f''(x)=0\) ou n'\(f''(x)\)est pas définie. Lorsque nous avons déterminé ces points, nous divisons le domaine de\(f\) en intervalles plus petits et déterminons le signe de\(f''\) sur chacun de ces intervalles plus petits. Si elle\(f''\) change de signe lorsque nous passons par un point\(x\), elle\(f\) change de concavité. Il est important de se rappeler qu'une fonction ne\(f\) peut pas changer de concavité à un point donné,\(x\) même si elle n'est pas définie\(f''(x)=0\) ou n'\(f''(x)\)est pas définie. Si, toutefois,\(f\) change de concavité en un point\(a\) et\(f\) est continu en un point\(a\), nous disons que le point\((a,f(a))\) est un point d'inflexion de\(f\).
S'il\(f\) est continu\(a\) et\(f\) change de concavité à\(a\), le point\((a, \,f(a))\) est un point d'inflexion de\(f\).
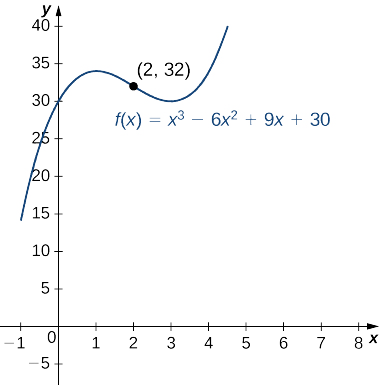
Pour la fonction,\(f(x)=x^3−6x^2+9x+30,\) déterminez tous les intervalles où\(f\) est concave vers le haut et tous les intervalles où il\(f\) est concave vers le bas. Listez tous les points d'inflexion pour\(f\). Utilisez un utilitaire graphique pour confirmer vos résultats.
Solution
Pour déterminer la concavité, nous devons trouver la dérivée seconde.\(f''(x).\) La dérivée première est\(f'(x)=3x^2−12x+9,\) telle que la dérivée seconde est.\(f''(x)=6x−12.\) Si la fonction change de concavité, elle se produit soit lorsque,\(f''(x)=0\) soit elle n'\(f''(x)\)est pas définie. Comme\(f''\) il est défini pour tous les nombres réels\(x\), il suffit de trouver où\(f''(x)=0\). En résolvant l'équation\(6x−12=0\), nous voyons que\(x=2\) c'est le seul endroit où l'\(f\)on pourrait changer de concavité. Nous testons maintenant les points sur les intervalles\((−∞,2)\) et\((2,∞)\) pour déterminer la concavité de\(f\). Les points\(x=0\) et\(x=3\) sont des points de test pour ces intervalles.
| Intervalle | Point d'essai | Panneau indiquant le\(f''(x)=6x−12\) point de test | Conclusion |
|---|---|---|---|
| \((−∞,2)\) | \(x=0\) | \ (f « (x) =6x−12 \) au point de test » style="vertical-align:middle ; ">− | \(f\)est concave vers le bas |
| \((2,∞)\) | \(x=3\) | \ (f « (x) =6x−12 \) au point de test » style="vertical-align:middle ; ">+ | \(f\)est concave vers le haut |
Nous concluons qu'elle\(f\) est concave vers le bas sur l'intervalle\((−∞,2)\) et concave vers le haut sur l'intervalle\((2,∞)\). Comme il\(f\) change de concavité à\(x=2\), le point\((2,f(2))=(2,32)\) est un point d'inflexion. La figure\(\PageIndex{7}\) confirme les résultats d'analyse.
Pour\(f(x)=−x^3+\frac{3}{2}x^2+18x\), trouvez tous les intervalles où il\(f\) est concave vers le haut et tous les intervalles où il\(f\) est concave vers le bas.
- Allusion
-
Trouvez où\(f''(x)=0\)
- Réponse
-
\(f\)est concave vers le haut sur l'intervalle\((−∞,\frac{1}{2})\) et concave vers le bas sur l'intervalle\((\frac{1}{2},∞)\)
Nous résumons maintenant, dans le tableau\(\PageIndex{4}\), les informations que les dérivées première et seconde d'une fonction\(f\) fournissent sur le graphe de\(f\), et illustrons ces informations dans la figure\(\PageIndex{8}\).
| Signe de\(f'\) | Signe de\(f''\) | Est\(f\) en hausse ou en baisse ? | Concavité |
|---|---|---|---|
| \ (f' \) » style="vertical-align:middle ; ">Positif | \ (f « \) » style="vertical-align:middle ; « >Positif | \ (f \) en hausse ou en baisse ? » style="vertical-align:middle ; « >Augmenter | Haut concave |
| \ (f' \) » style="vertical-align:middle ; ">Positif | \ (f « \) » style="vertical-align:middle ; « >Négatif | \ (f \) en hausse ou en baisse ? » style="vertical-align:middle ; « >Augmenter | Vers le bas concave |
| \ (f' \) » style="vertical-align:middle ; ">Négatif | \ (f « \) » style="vertical-align:middle ; « >Positif | \ (f \) en hausse ou en baisse ? » style="vertical-align:middle ; « >Décroissant | Haut concave |
| \ (f' \) » style="vertical-align:middle ; ">Négatif | \ (f « \) » style="vertical-align:middle ; « >Négatif | \ (f \) en hausse ou en baisse ? » style="vertical-align:middle ; « >Décroissant | Vers le bas concave |
Le deuxième test dérivé
Le premier test dérivé fournit un outil analytique pour trouver des extrêmes locaux, mais le second peut également être utilisé pour localiser des valeurs extrêmes. L'utilisation de la dérivée seconde peut parfois être une méthode plus simple que l'utilisation de la dérivée première.
Nous savons que si une fonction continue possède un extremum local, elle doit se produire à un point critique. Cependant, une fonction n'a pas besoin d'avoir un extremum local à un point critique. Nous examinons ici comment le test de la dérivée seconde peut être utilisé pour déterminer si une fonction possède un extremum local à un point critique. \(f\)Soit une fonction deux fois différenciable telle que\(f'(a)=0\) et\(f''\) soit continue sur un intervalle ouvert\(I\) contenant\(a\). Supposons\(f''(a)<0\). Puisque\(f''\) c'est continu\(I, f''(x)<0\) pour tous\(x∈I\) (Figure\(\PageIndex{9}\)). Ensuite, par corollaire\(3\),\(f'\) il y a une fonction décroissante terminée\(I\). Depuis\(f'(a)=0\), nous concluons que pour tous,\(x∈I, \,f'(x)>0\) si\(x<a\) et\(f'(x)<0\) si\(x>a\). Par conséquent, selon le premier test dérivé,\(f\) a un maximum local à\(x=a\).
D'un autre côté, supposons qu'il existe un point\(b\) tel que\(f'(b)=0\) mais\(f''(b)>0\). Puisque\(f''\) est continu sur un intervalle ouvert\(I\) contenant\(b\), alors\(f''(x)>0\) pour tous\(x∈I\) (Figure\(\PageIndex{9}\)). Ensuite, par corollaire\(3\), une fonction croissante\(f'\) est terminée\(I\). Depuis\(f'(b)=0\), nous concluons que pour tous\(x∈I\),\(f'(x)<0\) si\(x<b\) et\(f'(x)>0\) si\(x>b\). Par conséquent, selon le premier test dérivé,\(f\) a un minimum local à\(x=b.\)
Supposons que\(f'(c)=0\) et\(f''\) soit continu sur un intervalle contenant\(c\).
- Si\(f''(c)>0\),\(f\) a alors un minimum local à\(c\).
- Si\(f''(c)<0\),\(f\) a alors un maximum local à\(c\).
- \(f''(c)=0,\)Si c'est le cas, le test n'est pas concluant.
Notez que pour le cas iii. when\(f''(c)=0\), alors\(f\) peut avoir un maximum local, un minimum local, ou aucun des deux à\(c\). Par exemple, les fonctions\(f(x)=x^3, \; f(x)=x^4,\) ont\(f(x)=−x^4\) toutes des points critiques à\(x=0\). Dans chaque cas, la dérivée seconde est nulle à\(x=0\). Cependant, la fonction\(f(x)=x^4\) a un minimum local à\(x=0\) alors que la fonction\(f(x)=−x^4\) a un maximum local à\(x=0\), et la fonction\(f(x)=x^3\) n'a pas d'extremum local à\(x=0\).
Voyons maintenant comment utiliser le test de la dérivée seconde pour déterminer\(f\) s'il existe un maximum local ou un minimum local à un point critique\(c\) où\(f'(c)=0.\)
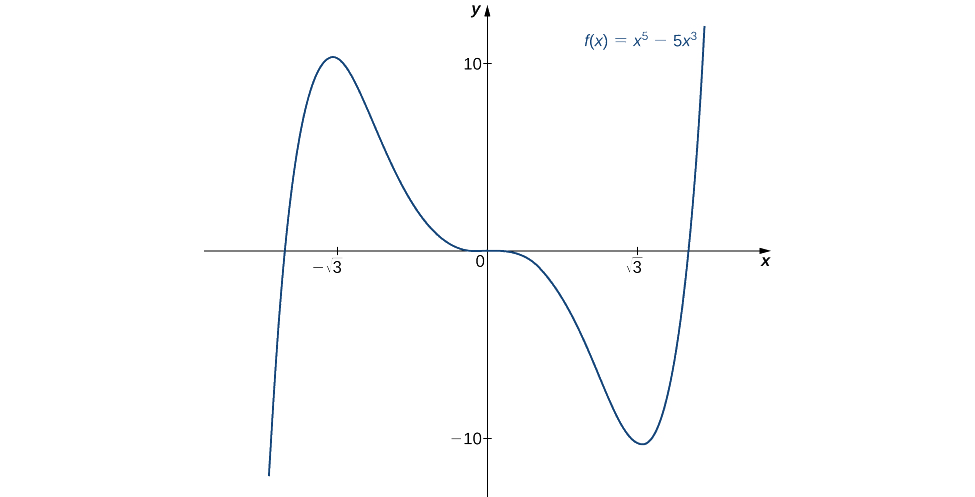
Utilisez la dérivée seconde pour trouver l'emplacement de tous les extrêmes locaux pour\(f(x)=x^5−5x^3.\)
Solution
Pour appliquer le deuxième test dérivé, nous devons d'abord déterminer les points critiques\(c\) où\(f'(c)=0\). Le dérivé est\(f'(x)=5x^4−15x^2\). Donc,\(f'(x)=5x^4−15x^2=5x^2(x^2−3)=0\) quand\(x=0,\,±\sqrt{3}\).
Pour déterminer s'il y\(f\) a un extremum local à l'un de ces points, nous devons évaluer le signe d'un extremum local\(f''\) à ces points. La deuxième dérivée est
\(f''(x)=20x^3−30x=10x(2x^2−3).\)
Dans le tableau suivant, nous évaluons la dérivée seconde à chacun des points critiques et utilisons le test de la dérivée seconde pour déterminer si elle\(f\) a un maximum local ou un minimum local à l'un de ces points.
| \(x\) | \(f''(x)\) | Conclusion |
|---|---|---|
| \ (x \) « >\(−\sqrt{3}\) | \ (f) « (x) \) » >\(−30\sqrt{3}\) | Maximum local |
| \ (x \) « >\(0\) | \ (f) « (x) \) » >\(0\) | Le second test dérivé n'est pas concluant |
| \ (x \) « >\(\sqrt{3}\) | \ (f) « (x) \) » >\(30\sqrt{3}\) | Minimum local |
Par le deuxième test dérivé, nous concluons qu'il\(f\) a un maximum local à\(x=−\sqrt{3}\) et\(f\) un minimum local à\(x=\sqrt{3}\). Le second test dérivé n'est pas concluant à\(x=0\). Pour déterminer s'il\(f\) y a un extrema local à,\(x=0,\) nous appliquons le premier test dérivé. Pour évaluer le signe de\(f'(x)=5x^2(x^2−3)\) pour\(x∈(−\sqrt{3},0)\) et\(x∈(0,\sqrt{3})\), laissez\(x=−1\) et\(x=1\) soyez les deux points de test. Depuis\(f'(−1)<0\) et\(f'(1)<0\), nous concluons que cela\(f\) diminue sur les deux intervalles et, par conséquent, qu'\(f\)il n'y a pas d'extrema local à,\(x=0\) comme le montre le graphique suivant.
Considérez la fonction\(f(x)=x^3−(\frac{3}{2})x^2−18x\). Les points sont\(c=3,\,−2\) satisfaisants\(f'(c)=0\). Utilisez le deuxième test de dérivée pour déterminer s'il y\(f\) a un maximum local ou un minimum local à ces points.
- Allusion
-
\(f''(x)=6x−3\)
- Réponse
-
\(f\)a un maximum local à\(−2\) et un minimum local à\(3\).
Nous avons maintenant développé les outils dont nous avons besoin pour déterminer où une fonction augmente et diminue, et nous avons acquis une compréhension de la forme de base du graphe. Dans la section suivante, nous discutons de ce qui arrive à une fonction.\(x→±∞.\) À ce stade, nous disposons de suffisamment d'outils pour fournir des graphiques précis d'une grande variété de fonctions.
Concepts clés
- S'il s'\(c\)agit d'un point critique\(f'(x)>0\) pour\(f\)\(x<c\) et\(f'(x)<0\) pour\(x>c\), alors\(f\) a un maximum local à\(c\).
- C'\(c\)est un point critique\(f'(x)<0\) pour\(f\)\(x<c\) et\(f'(x)>0\) pour\(x>c,\) alors\(f\) a un minimum local à\(c\).
- S'il est\(f''(x)>0\) supérieur à un intervalle\(I\), alors\(f\) est concave vers le haut\(I\).
- S'il est\(f''(x)<0\) supérieur à un intervalle\(I\), alors\(f\) est concave vers le bas\(I\).
- Si\(f'(c)=0\) tel est le cas\(f''(c)>0\),\(f\) a un minimum local à\(c\).
- Si\(f'(c)=0\) tel est le cas\(f''(c)<0\),\(f\) a un maximum local à\(c\).
- Si\(f'(c)=0\) tel est le cas\(f''(c)=0\), évaluez\(f'(x)\) à un point de test\(x\) à gauche\(c\) et à un point de test\(x\) à droite de\(c\), pour déterminer s'il y\(f\) a un extremum local à\(c\).
Lexique
- concave vers le bas
- s'il\(f\) est dérivable sur un intervalle\(I\) et\(f'\) est décroissant\(I\), alors\(f\) est concave vers le bas\(I\)
- haut concave
- si\(f\) est différenciable sur un intervalle\(I\) et\(f'\) augmente\(I\), alors\(f\) est concave vers le haut\(I\)
- concavité
- la courbe ascendante ou descendante du graphe d'une fonction
- test de concavité
- suppose qu'elle\(f\) est deux fois différenciable sur un intervalle\(I\) ; si elle est\(f''>0\) supérieure\(I\), alors\(f\) est concave vers le haut\(I\) ; si elle est\(f''<\) supérieure\(I\), alors\(f\) est concave vers le bas\(I\)
- premier test dérivé
- \(f\)soit une fonction continue sur un intervalle\(I\) contenant un point critique\(c\) tel qu'il\(f\) soit dérivable\(I\) sauf éventuellement à\(c\) ; si le signe\(f'\) passe de positif à négatif au fur et à mesure qu'il\(x\) augmente\(c\), alors \(f\)a un maximum local à\(c\) ; s'il\(f'\) change de signe de négatif à positif au fur et à mesure qu'il\(x\) augmente\(c\), alors\(f\) a un minimum local à\(c\) ; s'il\(f'\) ne change pas de signe à mesure qu'il\(x\) augmente\(c\), alors\(f\) n'a pas d'extremum local à\(c\)
- point d'inflexion
- s'il\(f\) est continu à\(c\) et\(f\) change de concavité à\(c\), le point\((c,f(c))\) est un point d'inflexion de\(f\)
- deuxième test dérivé
- suppose que\(f'(c)=0\) et\(f'\) 'est continu sur un intervalle contenant\(c\) ; si\(f''(c)>0\), alors\(f\) a un minimum local à\(c\) ; si\(f''(c)<0\), alors\(f\) a un maximum local à\(c\) ; si\(f''(c)=0\), alors le test n'est pas concluant


