2.5 : La définition précise d'une limite
- Page ID
- 198017
- Décrivez la définition epsilon-delta d'une limite.
- Appliquez la définition epsilon-delta pour déterminer la limite d'une fonction.
- Décrivez les définitions epsilon-delta des limites unilatérales et des limites infinies.
- Utilisez la définition d'epsilon-delta pour prouver les lois limites.
Vous êtes maintenant passé de la définition très informelle d'une limite dans l'introduction de ce chapitre à la compréhension intuitive d'une limite. À ce stade, vous devez avoir une idée très intuitive de ce que signifie la limite d'une fonction et de la façon dont vous pouvez la trouver. Dans cette section, nous transformons cette idée intuitive d'une limite en une définition formelle à l'aide d'un langage mathématique précis. La définition formelle d'une limite est probablement l'une des définitions les plus difficiles que vous rencontrerez au début de votre étude du calcul ; toutefois, tout effort que vous faites pour la concilier avec votre notion intuitive d'une limite vaut la peine. La compréhension de cette définition est la clé qui ouvre la voie à une meilleure compréhension du calcul.
Quantifier la proximité
Avant d'énoncer la définition formelle d'une limite, nous devons introduire quelques idées préliminaires. Rappelez-vous que la distance entre deux points\(a\) et\(b\) sur une ligne numérique est donnée par |\(a−b\) |.
- La déclaration |\(f(x)−L |<ε\) peut être interprétée comme suit : La distance entre\(f(x)\) et\(L\) est inférieure à\(ε\).
- La déclaration\(0<|x−a|<δ\) peut être interprétée comme suit :\(x≠a\) et la distance entre\(x\) et\(a\) est inférieure à\(δ\).
Il est également important d'examiner les équivalences suivantes pour la valeur absolue :
- La déclaration |\(f(x)−L|<ε\) est équivalente à la déclaration\(L−ε<f(x)<L+ε\).
- La déclaration\(0<|x−a|<δ\) est équivalente à la déclaration\(a−δ<x<a+δ\) et\(x≠a\).
Grâce à ces clarifications, nous pouvons énoncer la définition officielle de la limite epsilon-delta.
\(f(x)\)Soit défini pour l'ensemble\(x≠a\) sur un intervalle ouvert contenant\(a\). \(L\)Soyons un vrai chiffre. Alors
\[\lim_{x→a}f(x)=L \nonumber \]
si, pour chaque\(ε>0\), il existe un\(δ>0\), tel que si\(0<|x−a|<δ\), alors\(|f(x)−L|<ε\).
Cette définition peut sembler assez complexe d'un point de vue mathématique, mais elle devient plus facile à comprendre si on la décompose phrase par phrase. L'énoncé lui-même implique ce que l'on appelle un quantificateur universel (pour chaque\(ε>0\)), un quantificateur existentiel (il existe un\(δ>0\)) et, enfin, une déclaration conditionnelle (si\(0<|x−a|<δ\), alors\(|f(x)−L|<ε)\). Jetons un coup d'œil à Tableau\(\PageIndex{1}\), qui décompose la définition et traduit chaque partie.
| Définition | Traduction |
|---|---|
| 1. Pour tous\(ε>0\), | 1. Pour chaque distance positive par rapport\(ε\) à\(L\), |
| 2. Il existe un\(δ>0\), | 2. Il y a une distance positive par rapport\(δ\) à\(a\), |
| 3. de telle sorte que | 3. de telle sorte que |
| 4. Si\(0<|x−a|<δ\), alors\(|f(x)−L|<ε\). | 4. s'\(x\)il est plus\(δ\) proche que de\(a\) et\(x≠a\), alors\(f(x)\) est plus proche que\(ε\) de\(L\). |
Nous pouvons mieux comprendre cette définition en examinant la définition de manière géométrique. La figure\(\PageIndex{1}\) montre les valeurs possibles de\(δ\) pour différents choix de\(ε>0\) pour une fonction donnée\(f(x)\), un nombre\(a\) et une limite\(L\) à\(a\). Notez que lorsque nous choisissons des valeurs plus petites de\(ε\) (la distance entre la fonction et la limite), nous pouvons toujours trouver une valeur suffisamment\(δ\) petite pour que, si nous avons choisi une\(x\) valeur comprise\(δ\) entre\(a\), la valeur de\(f(x)\) se situe dans\(ε\) la limite \(L\).
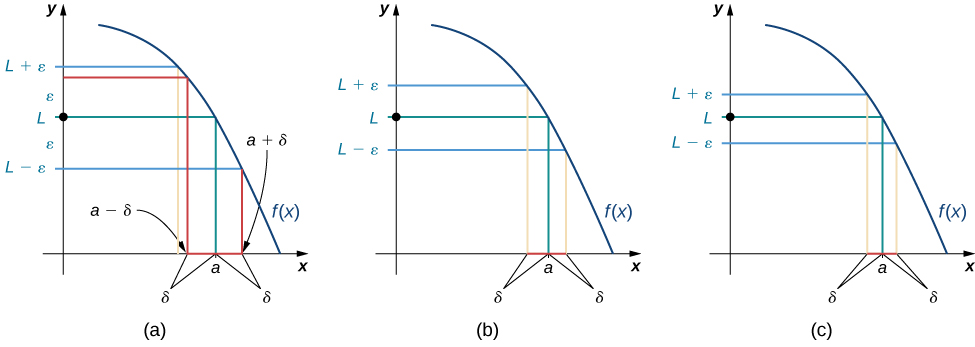
Consultez l'applet suivant pour essayer de trouver des valeurs de\(δ\) pour des valeurs sélectionnées de\(ε\) :
\(\PageIndex{1}\)L'exemple montre comment vous pouvez utiliser cette définition pour prouver une déclaration concernant la limite d'une fonction spécifique à une valeur spécifiée.
Prouve ça\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
Solution
Laissez\(ε>0\).
La première partie de la définition commence par « Pour tous\(ε>0\) », ce qui signifie que nous devons prouver que ce qui suit est vrai, quelle que\(ε\) soit la valeur positive choisie. En disant «\(ε>0\) Let », nous indiquons notre intention de le faire.
Choisissez\(δ=\frac{ε}{2}\).
La définition se poursuit par « il existe un »\(δ>0\). L'expression « il existe » dans un énoncé mathématique est toujours un signal pour une chasse au trésor. En d'autres termes, nous devons partir et trouver\(δ\). Alors, d'où\(δ=ε/2\) vient exactement ? Il existe deux approches de base pour effectuer un suivi\(δ\). L'une des méthodes est purement algébrique et l'autre est géométrique.
Nous commençons par aborder le problème d'un point de vue algébrique. Puisque finalement nous le voulons\(|(2x+1)−3|<ε\), nous commençons par manipuler cette expression :\(|(2x+1)−3|<ε\) est équivalent à\(|2x−2|<ε\), qui à son tour équivaut à\(|2||x−1|<ε\). Enfin, cela équivaut à\(|x−1|<ε/2\). Il semblerait donc que cela\(δ=ε/2\) soit approprié.
Nous pouvons également le découvrir\(δ\) grâce à des méthodes géométriques. La figure\(\PageIndex{2}\) montre comment cela se fait.
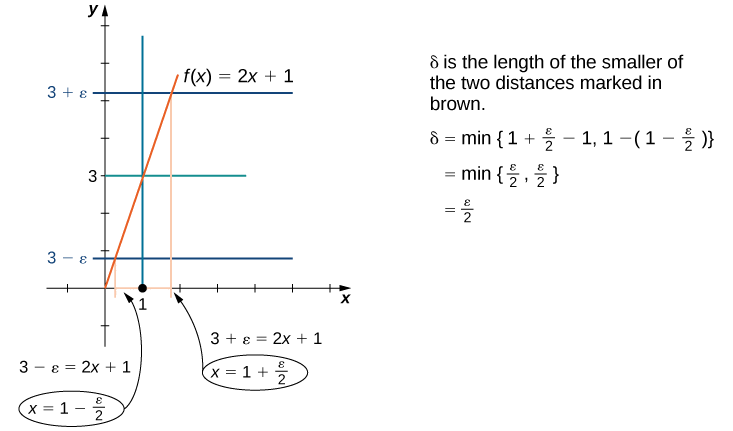
Supposons\(0<|x−1|<δ\). Quand\(δ\) a été choisi, notre objectif est de montrer que si\(0<|x−1|<δ\), alors\(|(2x+1)−3|<ε\). Pour prouver une déclaration de la forme « Si ceci, alors cela », nous commençons par supposer « ceci » et essayons d'obtenir « cela ».
Ainsi,
\(|(2x+1)−3|=|2x−2|\)propriété de valeur absolue
\(=|2(x−1)|\)
\(=|2||x−1|\)\(|2|=2\)
\(=2|x−1|\)
\(<2⋅δ \)voici où nous utilisons l'hypothèse que\(0<|x−1|<δ\)
\(=2⋅\frac{ε}{2}=ε\)voici où nous utilisons notre choix de\(δ=ε/2\)
Analyse
Dans cette partie de la preuve, nous avons commencé par\(|(2x+1)−3|\) utiliser notre hypothèse\(0<|x−1|<δ\) sur un élément clé de la chaîne des inégalités pour obtenir une valeur inférieure\(|(2x+1)−3|\) à ε. Nous aurions tout aussi bien pu manipuler l'inégalité supposée\(0<|x−1|<δ\) pour en arriver à ce qui\(|(2x+1)−3|<ε\) suit :
\(0<|x−1|<δ⇒|x−1|<δ\)
\(⇒−δ<x−1<δ\)
\(⇒−\frac{ε}{2}<x−1<\frac{ε}{2}\)
\(⇒−ε<2x−2<ε\)
\(⇒|2x−2|<ε\)
\(⇒|(2x+1)−3|<ε.\)
Par conséquent,\(\displaystyle \lim_{x→1} \;(2x+1)=3.\) (Une fois la preuve terminée, nous indiquons ce que nous avons accompli.)
Après avoir supprimé toutes les remarques, voici une version finale de la preuve :
Laissez\(ε>0\).
Choisissez\(δ=ε/2\).
Supposons\(0<|x−1|<δ\).
Ainsi,
\ (\ begin {align*} | (2x+1) −3| &= |2x−2| \ \ [4 points]
&=|2 (x−1) | \ \ [4 points]
&=|2||x−1| \ \ [4 points]
&=2|x−1| \ \ [4 points]
&<2⋅δ \ \ [4 points]
&=2⋅ \ frac {ε} {2} \ \ [4 points]
&=ε. \ end {align*} \)
Par conséquent,\(\displaystyle \lim_{x→1} \;(2x+1)=3\).
La stratégie de résolution de problèmes suivante résume le type de preuve que nous avons élaboré dans Example\(\PageIndex{1}\).
- Commençons la preuve par la déclaration suivante : Let\(ε>0\).
- Ensuite, nous devons obtenir une valeur pour\(δ\). Après avoir obtenu cette valeur, nous faisons la déclaration suivante, en remplissant le champ vide avec notre choix\(δ\) : Choisissez\(δ=\) _______.
- La déclaration suivante de la preuve devrait être (à ce stade, nous saisissons la valeur que nous avons donnée pour\(a\)) : Supposons\(0<|x−a|<δ\).
- Ensuite, sur la base de cette hypothèse, nous devons montrer que\(|f(x)−L|<ε\), où\(f(x)\) et\(L\) sont notre fonction\(f(x)\) et notre limite\(L\). À un moment donné, nous devons utiliser\(0<|x−a|<δ\).
- Nous concluons notre preuve par la déclaration : Donc,\(\displaystyle \lim_{x→a}f(x)=L\).
Complétez la preuve en\(\displaystyle \lim_{x→−1}\;(4x+1)=−3\) remplissant les champs.
Laissez _____.
Choisissez\(δ=\) _______.
Supposons que\(0<|x\) −_______|\(<δ\).
Ainsi, |________−________|=_____________________________________\(ε\).
Solution
Nous commençons par remplir les espaces où les choix sont spécifiés par la définition. Ainsi, nous avons
Laissez\(ε>0\).
Choisissez\(δ\) =_______.
Supposons\(0<|x−(−1)|<δ\). (ou de manière équivalente,\(0<|x+1|<δ\).)
Ainsi,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ\) _______\(ε\).
En nous concentrant sur la dernière ligne de preuve, nous voyons que nous devons choisir\(δ=\frac{ε}{4}\).
Nous terminons maintenant la rédaction finale de la preuve :
Laissez\(ε>0\).
Choisissez\(δ=\frac{ε}{4}\).
Supposons\(0<|x−(−1)|<δ\) (ou de manière équivalente,\(0<|x+1|<δ\).)
Ainsi,\(|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ=4(ε/4)=ε\).
Complétez la preuve en\(\displaystyle \lim_{x→2}\;(3x−2)=4\) remplissant les champs.
Laissez _______.
Choisissez\(δ\) =_______.
Supposons\(0<|x−\) ____\(|<\) ____.
Ainsi,
|_______−____|\(=\) ______________________________\(ε\).
Par conséquent,\(\displaystyle \lim_{x→2}\;(3x−2)=4\).
- Allusion
-
Suivez les grandes lignes de la stratégie de résolution de problèmes que nous avons élaborée dans son intégralité dans Example\(\PageIndex{2}\).
- Réponse
-
Laisser\(ε>0\) ; choisir\(δ=\frac{ε}{3}\) ; assumer\(0<|x−2|<δ\).
Ainsi,\(|(3x−2)−4|=|3x−6|=|3|⋅|x−2|<3⋅δ=3⋅(ε/3)=ε\).
Par conséquent,\(\displaystyle \lim_{x→2}(3x−2)=4\).
Dans\(\PageIndex{1}\) les exemples et\(\PageIndex{2}\) les preuves étaient assez simples, car les fonctions avec lesquelles nous travaillions étaient linéaires. Dans Exemple\(\PageIndex{3}\), nous voyons comment modifier la preuve pour l'adapter à une fonction non linéaire.
Prouve ça\(\displaystyle \lim_{x→2}x^2=4\).
Solution
1. Laissez\(ε>0\). La première partie de la définition commence par « Pour tous\(ε>0\) ». Nous devons donc prouver que ce qui suit est vrai, quelle que\(ε\) soit la valeur positive choisie. En disant «\(ε>0\) Let », nous indiquons notre intention de le faire.
2. Sans perte de généralité, supposons\(ε≤4\). Deux questions se posent : pourquoi voulons-nous\(ε≤4\) et pourquoi est-il acceptable de faire cette supposition ? En réponse à la première question : Plus tard, dans le processus de résolution de\(δ\), nous découvrirons que cela\(δ\) implique la quantité\(\sqrt{4−ε}\). Par conséquent, nous avons besoin de\(ε≤4\). En réponse à la deuxième question : si nous pouvons trouver\(δ>0\) que cela « fonctionne » pour\(ε≤4\), alors cela « fonctionnera » pour tout\(ε>4\) le monde également. Gardez à l'esprit que, bien qu'il soit toujours acceptable de placer une limite supérieure sur ε, il n'est jamais acceptable de placer une limite inférieure (autre que zéro)\(ε\).
3. Choisissez\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). La figure\(\PageIndex{3}\) montre comment nous avons fait ce choix de\(δ\).
![Ce graphique montre comment trouver le delta géométriquement pour un epsilon donné pour la preuve ci-dessus. Tout d'abord, la fonction f (x) = x^2 est tirée de [-1, 3]. Sur l'axe y, la limite 4 proposée est marquée et la ligne y=4 est tracée pour croiser la fonction at (2,4). Pour un epsilon donné, les points 4 + epsilon et 4 — epsilon sont marqués sur l'axe y au-dessus et en dessous de 4. Des lignes bleues sont tracées à partir de ces points pour intersecter la fonction, tandis que des lignes roses sont tracées depuis le point d'intersection jusqu'à l'axe x. Ces lignes atterrissent de part et d'autre de x=2. Ensuite, nous résolvons ces valeurs x, qui doivent être positives ici. La première est x^2 = 4 — epsilon, qui se simplifie en x = sqrt (4-epsilon). Le suivant est x^2 = 4 + epsilon, qui se simplifie en x = sqrt (4 + epsilon). Delta est la plus petite des deux distances, donc c'est le minimum de (2 — sqrt (4 — epsilon) et sqrt (4 + epsilon) — 2).](https://math.libretexts.org/@api/deki/files/12354/2.5.2.png)
4. Nous devons montrer : si\(0<|x−2|<δ\) c'est\(|x^2−4|<ε\) le cas, nous devons commencer par supposer
\(0<|x−2|<δ.\)
Nous n'avons pas vraiment besoin\(0<|x−2|\) (en d'autres termes,\(x≠2\)) de cette preuve. Depuis\(0<|x−2|<δ⇒|x−2|<δ\), il est normal de laisser tomber\(0<|x−2|\).
\(|x−2|<δ.\)
Par conséquent,
\(−δ<x−2<δ.\)
Souvenez-vous que\(δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}\). Ainsi,\(δ≥2−\sqrt{4−ε}\) et par conséquent\(−(2−\sqrt{4−ε})≤−δ\). Nous utilisons également\(δ≤\sqrt{4+ε}−2\) ici. Nous pouvons nous demander à ce stade : pourquoi avons-nous remplacé\(2−\sqrt{4−ε}\) le\(δ\) côté gauche de l'inégalité et le\(\sqrt{4+ε}−2\) côté droit de l'inégalité ? Si nous regardons la Figure\(\PageIndex{3}\), nous voyons que cela\(2−\sqrt{4−ε}\) correspond à la distance à gauche de\(2\) sur l'\(x\)axe -et\(\sqrt{4+ε}−2\) correspond à la distance sur la droite. Ainsi,
\(−(2−\sqrt{4−ε})≤−δ<x−2<δ≤\sqrt{4+ε}−2.\)
Nous simplifions l'expression sur la gauche :
\(−2+\sqrt{4−ε}<x−2<\sqrt{4+ε}−2\).
Ensuite, nous ajoutons 2 à toutes les parties de l'inégalité :
\(\sqrt{4−ε}<x<\sqrt{4+ε}.\)
Nous corrigeons tous les aspects de l'inégalité. Il n'y a rien de mal à le faire, car toutes les composantes de l'inégalité sont positives :
\(4−ε<x^2<4+ε.\)
Nous soustrayons\(4\) de toutes les composantes de l'inégalité :
\(−ε<x^2−4<ε.\)
Dernier,
\(|x^2−4|<ε.\)
5. Par conséquent,
\(\displaystyle \lim_{x→2}x^2=4.\)
Trouvez δ correspondant à\(ε>0\) pour prouver que\(\displaystyle \lim_{x→9}\sqrt{x}=3\).
- Allusion
-
Dessiner un graphique similaire à celui de l'exemple\(\PageIndex{3}\).
- Réponse
-
Choisissez\(δ=\text{min}\{9−(3−ε)^2,\;(3+ε)^2−9\}\).
L'approche géométrique qui permet de prouver que la limite d'une fonction prend une valeur spécifique fonctionne très bien pour certaines fonctions. En outre, la compréhension de la définition formelle de la limite fournie par cette méthode est inestimable. Cependant, nous pouvons également aborder les preuves limites d'un point de vue purement algébrique. Dans de nombreux cas, une approche algébrique peut non seulement nous fournir un aperçu supplémentaire de la définition, mais elle peut également s'avérer plus simple. En outre, l'approche algébrique est le principal outil utilisé pour prouver les déclarations concernant les limites. Par exemple,\(\PageIndex{4}\), nous adoptons une approche purement algébrique.
Prouvez que\(\displaystyle \lim_{x→−1}\;(x^2−2x+3)=6.\)
Solution
Utilisons les grandes lignes de notre stratégie de résolution de problèmes :
1. Laissez\(ε>0\).
2. Choisissez\(δ=\text{min}\{1,ε/5\}\). Ce choix de\(δ\) peut sembler étrange à première vue, mais il a été obtenu en examinant notre inégalité ultime souhaitée :\(∣(x^2−2x+3)−6∣<ε\). Cette inégalité est équivalente à\(|x+1|⋅|x−3|<ε\). À ce stade, la tentation de simplement choisir\(δ=\frac{ε}{x−3}\) est très forte. Malheureusement, notre choix de\(δ\) doit dépendre uniquement de ε et d'aucune autre variable. Si nous pouvons la remplacer\(|x−3|\) par une valeur numérique, notre problème peut être résolu. C'est ici que l'hypothèse\(δ≤1\) entre en jeu. Le choix de\(δ≤1\) cette option est arbitraire. Nous aurions tout aussi bien pu utiliser n'importe quel autre nombre positif. Selon certaines preuves, une plus grande prudence dans ce choix peut s'avérer nécessaire. Maintenant, depuis\(δ≤1\) et\(|x+1|<δ≤1\), nous sommes en mesure de le démontrer\(|x−3|<5\). Par conséquent,\(|x+1|⋅|x−3|<|x+1|⋅5\). À ce stade, nous réalisons que nous avons également besoin\(δ≤ε/5\). Ainsi, nous choisissons\(δ=\text{min}\{1,ε/5\}\).
3. Supposons\(0<|x+1|<δ\). Ainsi,
\[|x+1|<1\text{ and }|x+1|<\frac{ε}{5}. \nonumber \]
Depuis\(|x+1|<1\), nous pouvons en conclure que\(−1<x+1<1\). Ainsi, en soustrayant\(4\) de toutes les parties de l'inégalité, nous obtenons\(−5<x−3<−1\). Par conséquent,\(|x−3|<5\). Cela nous donne
\[\left|(x^2−2x+3)−6\right|=|x+1|⋅|x−3|<\frac{ε}{5}⋅5=ε.\nonumber \]
Par conséquent,
\[\lim_{x→−1}\;(x^2−2x+3)=6.\nonumber \]
Complétez la preuve que\(\displaystyle \lim_{x→1}x^2=1\).
Laisser\(ε>0\) ; choisir\(δ=\text{min}\{1,ε/3\}\) ; assumer\(0<|x−1|<δ\).
Depuis\(|x−1|<1\), nous pouvons en conclure que\(−1<x−1<1\). Ainsi,\(1<x+1<3\). Par conséquent,\(|x+1|<3\).
- Allusion
-
Utilisez Example\(\PageIndex{4}\) comme guide.
- Réponse
-
\(∣x^2−1∣=|x−1|⋅|x+1|<ε/3⋅3=ε\)
Vous constaterez qu'en général, plus une fonction est complexe, plus il est probable que l'approche algébrique soit la plus facile à appliquer. L'approche algébrique est également plus utile pour prouver les déclarations concernant les limites.
Prouver les lois
Nous montrons maintenant comment utiliser la définition epsilon-delta d'une limite pour établir une preuve rigoureuse de l'une des lois limites. L'inégalité triangulaire est utilisée à un point clé de la preuve. Nous examinons donc d'abord cette propriété clé de valeur absolue.
L'inégalité triangulaire indique que si\(a\) et\(b\) sont des nombres réels, alors\(|a+b|≤|a|+|b|\).
Nous prouvons la loi limite suivante : Si\(\displaystyle \lim_{x→a}f(x)=L\) et\(\displaystyle \lim_{x→a}g(x)=M\), alors\(\displaystyle \lim_{x→a}\;(f(x)+g(x))=L+M\).
Laissez\(ε>0\).
Choisissez de\(δ_1>0\) telle sorte que si\(0<|x−a|<δ_1\), alors\(|f(x)−L|<ε/2\).
Choisissez de\(δ_2>0\) telle sorte que si\(0<|x−a|<δ_2\), alors\(|g(x)−M|<ε/2\).
Choisissez\(δ=\text{min}\{δ_1,δ_2\}\).
Supposons\(0<|x−a|<δ\).
Ainsi,
\(0<|x−a|<δ_1\)et\(0<|x−a|<δ_2\).
Par conséquent,
\ [\ begin {align*} | (f (x) +g (x)) − (L+M) |&=| (f (x) −L) + (g (x) −M) | \ \ [4 points]
&≤|f (x) −L|+|G (x) −M| \ \ [4 points]
&< \ frac {ε} {2} + \ {frac ε} {2} =ε \ end {align*}. \ aucun numéro \]
□
Nous allons maintenant examiner ce que signifie l'absence de limite. La limite\(\displaystyle \lim_{x→a}f(x)\) n'existe pas s'il n'existe pas de nombre réel\(L\) pour lequel\(\displaystyle \lim_{x→a}f(x)=L\). Ainsi, pour tous les nombres réels\(L\),\(\displaystyle \lim_{x→a}f(x)≠L\). Pour comprendre ce que cela signifie, nous examinons chaque partie de la définition de\(\displaystyle \lim_{x→a}f(x)=L\) conjointement avec son contraire. Une traduction de la définition est donnée dans le tableau\(\PageIndex{2}\).
| Définition | Opposé |
|---|---|
| 1. Pour tous\(ε>0\), | 1. Il existe\(ε>0\) pour que |
| 2. Il existe un\(δ>0\), de sorte que | 2. pour chaque\(δ>0\), |
| 3. Si\(0<|x−a|<δ\), alors\(|f(x)−L|<ε\). | 3. Il y a une\(x\) satisfaction\(0<|x−a|<δ\) pour que\(|f(x)−L|≥ε\). |
Enfin, nous pouvons indiquer ce que signifie l'absence de limite. La limite\(\displaystyle \lim_{x→a}f(x)\) n'existe pas si pour chaque nombre réel\(L\), il existe un nombre réel\(ε>0\) afin que pour tous\(δ>0\), il y ait un\(x\) satisfaisant\(0<|x−a|<δ\), de sorte que\(|f(x)−L|≥ε\). Appliquons cela dans\(\PageIndex{5}\) l'exemple pour montrer qu'aucune limite n'existe.
Montrez que\(\displaystyle \lim_{x→0}\frac{|x|}{x}\) cela n'existe pas. Le graphique de\(f(x)=|x|/x\) est présenté ici :
0, et il s'agit d'une ligne sans pente qui commence sur l'axe y dans un cercle ouvert (1,0)." src="https://math.libretexts.org/@api/dek...2355/2.5.3.png">
Solution
Supposons que\(L\) c'est un candidat pour une limite. Choisissez\(ε=1/2\).
Laissez\(δ>0\). \(L≥0\)Soit\(L<0\). Si\(L≥0\), alors laissez\(x=−δ/2\).
Ainsi,
\(|x−0|=∣−\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
et
\(\left|\frac{∣−\frac{δ}{2}∣}{−\frac{δ}{2}}−L\right|=|−1−L|=L+1≥1>\frac{1}{2}=ε\).
D'un autre côté, si\(L<0\), alors laissez\(x=δ/2\). Ainsi,
\(|x−0|=∣\frac{δ}{2}−0∣=\frac{δ}{2}<δ\)
et
\(\left|\frac{∣\frac{δ}{2}∣}{\frac{δ}{2}}−L\right|=|1−L|=|L|+1≥1>\frac{1}{2}=ε\).
Ainsi, pour n'importe quelle valeur de\(L\),\(\displaystyle \lim_{x→0}\frac{|x|}{x}≠L.\)
Limites unilatérales
Tout comme nous avons d'abord acquis une compréhension intuitive des limites, puis nous sommes passés à une définition plus rigoureuse d'une limite, nous revoyons maintenant les limites unilatérales. Pour ce faire, nous modifions la définition epsilon-delta d'une limite afin de donner des définitions epsilon-delta formelles pour les limites situées à droite et à gauche en un point. Ces définitions ne nécessitent que de légères modifications par rapport à la définition de la limite. Dans la définition de la limite à partir de la droite, l'inégalité\(0<x−a<δ\) remplace\(0<|x−a|<δ\), ce qui garantit que nous ne prenons en compte\(x\) que les valeurs supérieures à (à droite de)\(a\). De même, dans la définition de la limite depuis la gauche, l'inégalité\(−δ<x−a<0\) remplace\(0<|x−a|<δ\), ce qui garantit que nous ne prenons en compte\(x\) que les valeurs inférieures à (à gauche de)\(a\).
Limite depuis la droite :\(f(x)\) À définir sur un intervalle ouvert du formulaire\((a,b)\) où\(a<b\). Alors
\[\lim_{x→a^+}f(x)=L \nonumber \]
si pour chaque\(ε>0\), il existe un\(δ>0\), tel que si\(0<x−a<δ\), alors\(|f(x)−L|<ε\).
Limite depuis la gauche :\(f(x)\) À définir sur un intervalle ouvert du formulaire\((b,c)\) où\(b<c\). Ensuite,
\[\lim_{x→c^−}f(x)=L \nonumber \]
si pour chaque\(ε>0\), il existe un\(δ>0\) tel que si\( −δ<x−c<0\), alors\(|f(x)−L|<ε\).
Prouvez que
\[\lim_{x→4^+}\sqrt{x−4}=0.\nonumber \]
Solution
Laissez\(ε>0\).
Choisissez\(δ=ε^2\). Puisque nous voulons en fin de compte\(∣\sqrt{x−4}−0∣<ε\), nous manipulons cette inégalité pour obtenir\(\sqrt{x−4}<ε\) ou, de manière équivalente\(0<x−4<ε^2\), faire\(δ=ε^2\) un choix clair. Nous pouvons également déterminer de\(δ\) manière géométrique, comme le montre la figure\(\PageIndex{4}\).
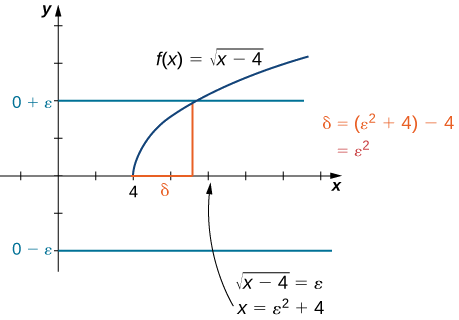
Supposons\(0<x−4<δ\). Ainsi,\(0<x−4<ε^2\). Par conséquent,\(0<\sqrt{x−4}<ε\). Enfin,\(\left|\sqrt{x−4}−0\right|<ε\). Par conséquent,\(\displaystyle \lim_{x→4^+}\sqrt{x−4}=0\).
Trouvez\(δ\) correspondant à\(ε\) pour prouver que\(\displaystyle \lim_{x→1^−}\sqrt{1−x}=0\).
- Allusion
-
Esquissez le graphique et utilisez Example\(\PageIndex{6}\) comme guide de résolution.
- Réponse
-
\(δ=ε^2\)
Limites infinies
Nous concluons le processus de conversion de nos idées intuitives sur divers types de limites en définitions formelles rigoureuses en poursuivant une définition formelle des limites infinies. Pour cela\(\displaystyle \lim_{x→a}f(x)=+∞\), nous voulons que les valeurs de la fonction soient de plus en plus grandes\(f(x)\) à mesure que l'on\(x\) s'en rapproche\(a\). Au lieu d'exiger que\(|f(x)−L|<ε\) le terme « arbitrairement petit\(ε\) » soit « suffisamment petit\(0<|x−a|<δ\) »\(δ\), nous voulons « arbitrairement grand\(f(x)>M\) », « positif »\(M\) lorsqu'il s'agit\(0<|x−a|<δ\) de « suffisamment petit »\(δ\). La figure\(\PageIndex{5}\) illustre cette idée en montrant la valeur de\(δ\) pour des valeurs de\(M\).
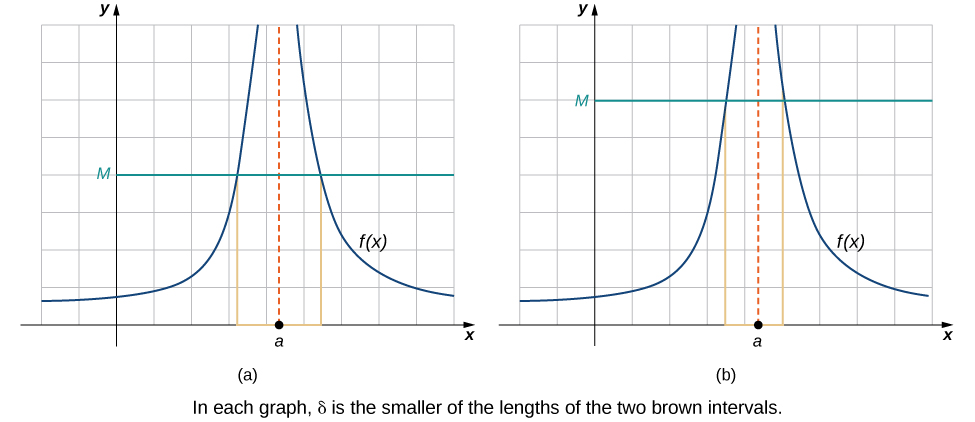
Figure\(\PageIndex{5}\) : Ces graphiques tracent les valeurs de\(δ\) pour\(M\) pour pour le montrer\(\displaystyle \lim_{x→a}f(x)=+∞\).
Laissez\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have an infinite limit
\[\lim_{x→a}f(x)=+∞ \nonumber \]
si pour chaque\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)>M\).
Laissez\(f(x)\) be defined for all \(x≠a\) in an open interval containing \(a\). Then, we have a negative infinite limit
\[\lim_{x→a}f(x)=−∞ \nonumber \]
si pour chaque\(M>0\), there exists \(δ>0\) such that if \(0<|x−a|<δ\), then \(f(x)<−M\).
Prouvez que\(\displaystyle \lim_{x→3}\frac{1}{(x-3)^2}=\infty.\)
Solution
Nous utilisons une approche très similaire à notre précédente stratégie de résolution de problèmes. Nous trouvons d'abord une solution appropriée\(δ>0\). Ensuite, nous rédigeons notre preuve.
Étape 1 : Nous trouvons d'abord une solution appropriée\(δ>0\).
1. \(M\)Soit n'importe quel nombre réel tel que\(M>0\).
2. Laissez\(f(x) = \dfrac{1}{(x-3)^2} > M\). Ensuite, nous résolvons l'expression\(x - 3\).
En multipliant les deux côtés de l'inégalité par la quantité positive\((x - 3)^2\) et en divisant les deux côtés par la quantité positive,\(M\) nous obtenons :
\[ \frac{1}{M} > (x-3)^2 \nonumber \]
En prenant la racine carrée des deux côtés, nous avons,
\[ \sqrt{\frac{1}{M}} > |x - 3|. \qquad \quad\left(\text{Remember that }\sqrt{x^2} = |x|.\right)\nonumber \]
La réécriture de cette déclaration nous donne,\(0 < |x-3| < \sqrt{\dfrac{1}{M}}\). De là, nous choisissons\(δ = \sqrt{\dfrac{1}{M}}\).
Étape 2 : Maintenant, nous écrivons une preuve.
3. Laisse\(δ = \sqrt{\dfrac{1}{M}}\) et assume\(0 < |x-3| < δ = \sqrt{\dfrac{1}{M}}\).
Ainsi,
\[ |x-3| < \sqrt{\frac{1}{M}}. \nonumber \]
La mise au carré des deux côtés nous donne,
\[ (x-3)^2 < \frac{1}{M}. \nonumber \]
En prenant la réciprocité des deux côtés (et en gardant à l'esprit que cela inversera le sens de l'inégalité),
\[ \dfrac{1}{(x-3)^2} > M. \nonumber \]
Par conséquent, nous avons prouvé que
\[\lim_{x→3}\frac{1}{(x-3)^2}=\infty.\nonumber \]
Une preuve très similaire sera nécessaire pour une limite égale à\(-\infty\).
Notez qu'une approche de limite unilatérale devra souvent être adoptée avec ce type de limite. Par exemple, pour prouver :\(\displaystyle \lim_{x\to 0^+}\frac{1}{x} = \infty\).
Concepts clés
- La notion intuitive d'une limite peut être convertie en une définition mathématique rigoureuse connue sous le nom de définition epsilon-delta de la limite.
- La définition epsilon-delta peut être utilisée pour prouver les déclarations concernant les limites.
- La définition epsilon-delta d'une limite peut être modifiée pour définir des limites unilatérales.
- Une définition similaire d'une limite infinie peut être utilisée pour prouver des déclarations concernant des limites infinies.
Lexique
- définition de la limite en epsilon-delta
- \(\displaystyle \lim_{x→a}f(x)=L\)si pour chaque\(ε>0\), il existe un\(δ>0\) tel que si\(0<|x−a|<δ\), alors\(|f(x)−L|<ε\)
- inégalité triangulaire
- Si\(a\) et\(b\) sont des nombres réels, alors\(|a+b|≤|a|+|b|\)
- définition formelle d'une limite infinie
- \(\displaystyle \lim_{x→a}f(x)=\infty\)si pour chaque\(M>0\), il existe un\(δ>0\) tel que si\(0<|x−a|<δ\), alors\(f(x)>M\)
\(\displaystyle \lim_{x→a}f(x)=-\infty\) si pour chaque\(M>0\), il existe un\(δ>0\) tel que si\(0<|x−a|<δ\), alors\(f(x)<-M\)
Contributeurs et attributions
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College), added Example \(\PageIndex{7}\) and entries for infinite limits under Key Concepts and the Glossary.


