2.3 : Les lois limites

Objectifs d'apprentissage

• Reconnaissez les lois limites de base.
• Utilisez les lois de limite pour évaluer la limite d'une fonction.
• Evaluez la limite d'une fonction par factorisation.
• Utilisez les lois limites pour évaluer la limite d'une fonction polynomiale ou rationnelle.
• Évaluez la limite d'une fonction en factorisant ou en utilisant des conjugués.
• Évaluez la limite d'une fonction à l'aide du théorème de compression.

Dans la section précédente, nous avons évalué les limites en examinant des graphiques ou en construisant un tableau de valeurs. Dans cette section, nous établissons des lois pour le calcul des limites et apprenons comment appliquer ces lois. Dans le projet étudiant à la fin de cette section, vous avez la possibilité d'appliquer ces lois limites pour dériver la formule de l'aire d'un cercle en adaptant une méthode conçue par le mathématicien grec Archimède. Nous commençons par reformuler deux résultats de limites utiles de la section précédente. Ces deux résultats, ainsi que les lois limites, servent de base au calcul de nombreuses limites.

Evaluer les limites à l'aide des lois

Les deux premières lois limites ont été énoncées précédemment et nous les répétons ici. Ces résultats de base, associés aux autres lois limites, nous permettent d'évaluer les limites de nombreuses fonctions algébriques.

Résultats limites de base

Pour tout nombre réel$a$ et toute constante$c$,

1. $\displaystyle \lim_{x→a}x=a$
2. $\displaystyle \lim_{x→a}c=c$

Exemple$\PageIndex{1}$: Evaluating a Basic Limit

Évaluez chacune des limites suivantes à l'aide des « Résultats des limites de base ».

1. $\displaystyle \lim_{x→2}x$
2. $\displaystyle \lim_{x→2}5$

Solution

1. La limite$x$ des$x$ approches$a$ est$a$ :$\displaystyle \lim_{x→2}x=2$.
2. La limite d'une constante est cette constante :$\displaystyle \lim_{x→2}5=5$.

Nous examinons maintenant les lois limites, les propriétés individuelles des limites. Les preuves que contiennent ces lois sont omises ici.

Lois relatives aux limites

$g(x)$Soit$f(x)$ défini pour tout$x≠a$ sur un intervalle ouvert contenant$a$. Supposons que$L$ et$M$ sont des nombres réels tels que$\displaystyle \lim_{x→a}f(x)=L$ et$\displaystyle \lim_{x→a}g(x)=M$. $c$Soyons une constante. Ensuite, chacune des déclarations suivantes s'applique :

• Loi de somme pour les limites :

$$\displaystyle \lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M \nonumber$$

• Loi de différence pour les limites :

$$\displaystyle \lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M \nonumber$$

• Loi multiple constante pour les limites :

$$\displaystyle \lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber$$

• Loi sur les produits concernant les limites :

$$\displaystyle \lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M \nonumber$$

• Loi du quotient pour les limites :

$$\displaystyle \lim_{x→a}\frac{f(x)}{g(x)}=\frac{\displaystyle \lim_{x→a}f(x)}{\displaystyle \lim_{x→a}g(x)}=\frac{L}{M} \nonumber$$

pour$M≠0$.

• Loi de puissance pour les limites :

$$\displaystyle \lim_{x→a}\big(f(x)\big)^n=\big(\lim_{x→a}f(x)\big)^n=L^n \nonumber$$

pour chaque entier positif$n$.

• Loi fondamentale pour les limites :

$$\displaystyle \lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a} f(x)}=\sqrt[n]{L} \nonumber$$

pour tous$L$ si$n$ est impair et pour$L≥0$ si$n$ est pair.

Nous nous entraînons maintenant à appliquer ces lois limites pour évaluer une limite.

Exemple$\PageIndex{2A}$: Evaluating a Limit Using Limit Laws

Utilisez les lois limites pour évaluer $$\lim_{x→−3}(4x+2). \nonumber$$

Solution

Appliquons les lois limites étape par étape pour être sûrs de comprendre comment elles fonctionnent. Nous devons garder à l'esprit l'exigence selon laquelle, à chaque application d'une loi limite, les nouvelles limites doivent exister pour que la loi limite soit appliquée.

$$\begin{align*} \lim_{x→−3}(4x+2) &= \lim_{x→−3} 4x + \lim_{x→−3} 2 & & \text{Apply the sum law.}\\[4pt] &= 4⋅\lim_{x→−3} x + \lim_{x→−3} 2 & & \text{Apply the constant multiple law.}\\[4pt] &= 4⋅(−3)+2=−10. & & \text{Apply the basic limit results and simplify.} \end{align*}$$

Exemple$\PageIndex{2B}$: Using Limit Laws Repeatedly

Utilisez les lois limites pour évaluer $$\lim_{x→2}\frac{2x^2−3x+1}{x^3+4}. \nonumber$$

Solution

Pour trouver cette limite, nous devons appliquer les lois de limitation plusieurs fois. Encore une fois, nous devons garder à l'esprit que lorsque nous réécrivons la limite en termes d'autres limites, chaque nouvelle limite doit exister pour que la loi des limites soit appliquée.

\ [\ begin {align*} \ lim_ {x→2} \ frac {2x^2−3x+1} {x^3+4} &= \ frac {\ displaystyle \ lim_ {x→2} (2x^2−3x+1)} {\ displaystyle \ lim_ {x→2} (x^3+4)} & & \ text {Appliquez la loi du quotient, assurez-vous cela} (2) ^3+4⁄0. \ \ [4 points]
&= \ frac {\ displaystyle 2⋅ \ lim_ {x→2} x^2−3⋅ \ lim_ {x→2} x+ \ lim_ {x→2} 1} {\ displaystyle \ lim_ {x→ 2} x^3+ \ lim_ {x→2} 4} & & \ text {Appliquez la loi de la somme et la loi multiple constante.} \ \ [4pt]
&= \ frac {\ displaystyle 2⋅ \ left (\ lim_ {x→2} x \ right) ^2−3⋅ \ lim_ {x→2} x+ \ lim_ {x→2} 1} {\ displaystyle \ left (\ lim_ {x→2} x \ right) ^3+ \ lim_ {x→2} 4} & \ text {Appliquez la loi de puissance.} \ \ [4 points]
&= \ frac {2 (4) −3 (2) +1} {(2) ^3+4} = \ frac {1} {4}. & & \ text {Appliquez les lois limites de base et simplifiez.} \ end {align*} \]

Exercice$\PageIndex{2}$

Utilisez les lois limites pour évaluer$\displaystyle \lim_{x→6}(2x−1)\sqrt{x+4}$. À chaque étape, indiquez la loi limite appliquée.

Allusion

Commencez par appliquer la loi sur les produits.

Réponse

$11\sqrt{10}$

Limites des fonctions polynomiales et rationnelles

À ce jour, vous avez probablement remarqué que, dans chacun des exemples précédents, il a été le cas que$\displaystyle \lim_{x→a}f(x)=f(a)$. Ce n'est pas toujours vrai, mais cela vaut pour tous les polynômes, quel que soit le choix$a$ et pour toutes les fonctions rationnelles, à toutes les valeurs$a$ pour lesquelles la fonction rationnelle est définie.

Limites des fonctions polynomiales et rationnelles

Fonctions polynomiales de type$p(x)$ Let et$q(x)$ Be. $a$Soyons un vrai chiffre. Ensuite,

$$\lim_{x→a}p(x)=p(a) \nonumber$$

$$\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)} \nonumber$$

quand$q(a)≠0$.

Pour vérifier que ce théorème est valable, considérez le polynôme

$$p(x)=c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0. \nonumber$$

En appliquant la somme, le multiple constant et les lois de puissance, nous obtenons

$$\begin{align*} \lim_{x→a}p(x) &= \lim_{x→a}(c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0) \\[4pt] &= c_n\left(\lim_{x→a}x\right)^n+c_{n−1}\left(\lim_{x→a}x\right)^{n−1}+⋯+c_1\left(\lim_{x→a}x\right)+\lim_{x→a}c_0 \\[4pt] &= c_na^n+c_{n−1}a^{n−1}+⋯+c_1a+c_0 \\[4pt] &= p(a) \end{align*}$$

Il découle maintenant de la loi du quotient que si$p(x)$ et$q(x)$ sont des polynômes pour lesquels$q(a)≠0$,

alors

$$\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}. \nonumber$$

Exemple$\PageIndex{3}$: Evaluating a Limit of a Rational Function

Évaluez le$\displaystyle \lim_{x→3}\frac{2x^2−3x+1}{5x+4}$.

Solution

Puisque 3 est dans le domaine de la fonction rationnelle$f(x)=\displaystyle \frac{2x^2−3x+1}{5x+4}$, nous pouvons calculer la limite en remplaçant 3 par$x$ dans la fonction. Ainsi,

$$\lim_{x→3}\frac{2x^2−3x+1}{5x+4}=\frac{10}{19}. \nonumber$$

Exercice$\PageIndex{3}$

Évaluer$\displaystyle \lim_{x→−2}(3x^3−2x+7)$.

Allusion

Utiliser les LIMITES DES FONCTIONS POLYNOMIALES ET RATIONNELLES comme référence

Réponse

−13

Techniques supplémentaires d'évaluation des limites

Comme nous l'avons vu, nous pouvons facilement évaluer les limites des polynômes et les limites de certaines fonctions rationnelles (mais pas toutes) par substitution directe. Cependant, comme nous l'avons vu dans la section introductive sur les limites, il est certainement possible$\displaystyle \lim_{x→a}f(x)$ d'exister lorsqu'elles ne$f(a)$ sont pas définies. L'observation suivante nous permet d'évaluer de nombreuses limites de ce type :

Si pour tout cela$x≠a,\;f(x)=g(x)$ sur un intervalle ouvert contenant$a$, alors

$$\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x). \nonumber$$

Pour mieux comprendre cette idée, considérez la limite$\displaystyle \lim_{x→1}\dfrac{x^2−1}{x−1}$.

La fonction

$$f(x)=\dfrac{x^2−1}{x−1}=\dfrac{(x−1)(x+1)}{x−1}\nonumber$$

et la fonction$g(x)=x+1$ sont identiques pour toutes les valeurs de$x≠1$. Les graphiques de ces deux fonctions sont présentés dans la figure$\PageIndex{1}$.

Figure$\PageIndex{1}$ : Les graphes de$f(x)$ et$g(x)$ sont identiques pour tous$x≠1$. Leurs limites à 1 sont égales.

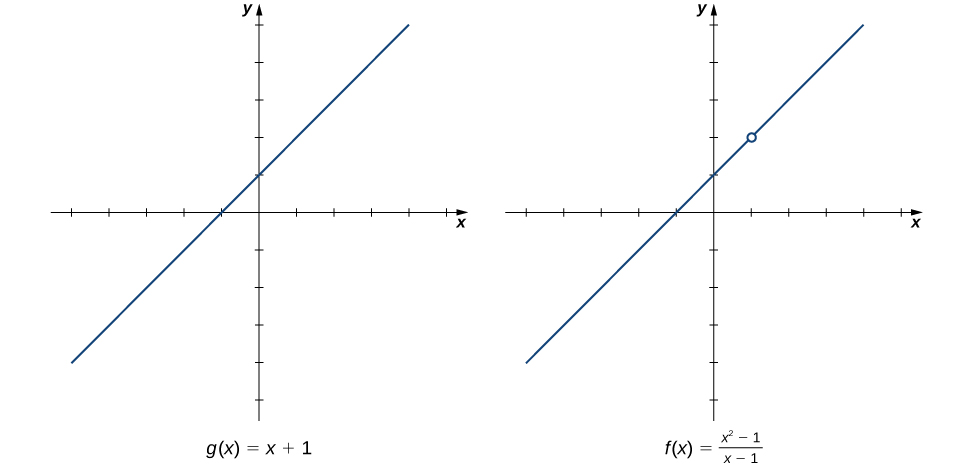
Nous voyons que

$$\lim_{x→1}\dfrac{x^2−1}{x−1}=\lim_{x→1}\dfrac{(x−1)(x+1)}{x−1}=\lim_{x→1}\,(x+1)=2.\nonumber$$

La limite a la forme$\displaystyle \lim_{x→a}f(x)/g(x)$, l'endroit$\displaystyle\lim_{x→a}f(x)=0$ et$\displaystyle\lim_{x→a}g(x)=0$. (Dans ce cas, nous disons que cela$f(x)/g(x)$ a la forme indéterminée$0/0$.) La stratégie de résolution de problèmes suivante fournit un aperçu général de l'évaluation des limites de ce type.

Stratégie de résolution de problèmes : calcul d'une limite lorsque$f(x)/g(x)$ has the Indeterminate Form $0/0$

1. Tout d'abord, nous devons nous assurer que notre fonction a la forme appropriée et ne peut pas être évaluée immédiatement à l'aide des lois limites.
2. Nous devons ensuite trouver une fonction égale à$h(x)=f(x)/g(x)$ for all$x≠a$ sur un intervalle contenant a. Pour ce faire, nous devrons peut-être essayer une ou plusieurs des étapes suivantes :
   1. Si$f(x)$ et$g(x)$ sont des polynômes, nous devons factoriser chaque fonction et annuler tous les facteurs communs.
   2. Si le numérateur ou le dénominateur contient une différence impliquant une racine carrée, nous devons essayer de multiplier le numérateur et le dénominateur par le conjugué de l'expression impliquant la racine carrée.
   3. S'il s'$f(x)/g(x)$agit d'une fraction complexe, nous commençons par la simplifier.
3. Enfin, nous appliquons les lois limites.

Les exemples suivants illustrent l'utilisation de cette stratégie de résolution de problèmes. L'exemple$\PageIndex{4}$ illustre la technique des facteurs et des annulations ; l'exemple$\PageIndex{5}$ montre la multiplication par un conjugué. Dans l'exemple$\PageIndex{6}$, nous cherchons à simplifier une fraction complexe.

Exemple$\PageIndex{4}$: Evaluating a Limit by Factoring and Canceling

Évaluer$\displaystyle\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}$.

Solution

Étape 1 La fonction$f(x)=\dfrac{x^2−3x}{2x^2−5x−3}$ n'est pas définie pour$x=3$. En fait, si nous substituons 3 à la fonction que nous obtenons$0/0$, qui n'est pas définie. L'affacturage et l'annulation sont une bonne stratégie :

$$\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}=\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}\nonumber$$

Étape 2 Pour tous$x≠3,\dfrac{x^2−3x}{2x^2−5x−3}=\dfrac{x}{2x+1}$ Par conséquent,

$$\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}=\lim_{x→3}\dfrac{x}{2x+1}.\nonumber$$

Étape 3 Évaluez à l'aide des lois limites :

$$\lim_{x→3}\dfrac{x}{2x+1}=\dfrac{3}{7}.\nonumber$$

Exercice$\PageIndex{4}$

Évaluer$\displaystyle \lim_{x→−3}\dfrac{x^2+4x+3}{x^2−9}$.

Allusion

Suivez les étapes de la stratégie de résolution de problèmes

Réponse

$\dfrac{1}{3}$

Exemple$\PageIndex{5}$: Evaluating a Limit by Multiplying by a Conjugate

Évaluer$\displaystyle \lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}$.

Solution

Étape 1 $\displaystyle \dfrac{\sqrt{x+2}−1}{x+1}$a la forme$0/0$ à −1. Commençons par multiplier par le conjugué de$\sqrt{x+2}+1$$\sqrt{x+2}−1$, sur le numérateur et le dénominateur :

$$\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}=\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}⋅\dfrac{\sqrt{x+2}+1}{\sqrt{x+2}+1}.\nonumber$$

Étape 2 Nous multiplions ensuite le numérateur. Nous ne multiplions pas le dénominateur parce que nous espérons que$(x+1)$ le dénominateur s'annule à la fin :

$$=\lim_{x→−1}\dfrac{x+1}{(x+1)(\sqrt{x+2}+1)}.\nonumber$$

Étape 3 Ensuite, nous annulons :

$$= \lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}.\nonumber$$

Étape 4. Enfin, nous appliquons les lois limites :

$$\lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}=\dfrac{1}{2}.\nonumber$$

Exercice$\PageIndex{5}$

Évaluer$\displaystyle \lim_{x→5}\dfrac{\sqrt{x−1}−2}{x−5}$.

Allusion

Suivez les étapes de la stratégie de résolution de problèmes

Réponse

$\dfrac{1}{4}$

Exemple$\PageIndex{6}$: Evaluating a Limit by Simplifying a Complex Fraction

Évaluer$\displaystyle \lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}$.

Solution

Étape 1 $\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}$a le formulaire$0/0$ à 1. On simplifie la fraction algébrique en la multipliant par$2(x+1)/2(x+1)$ :

$$\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}=\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}⋅\dfrac{2(x+1)}{2(x+1)}.\nonumber$$

Étape 2 Ensuite, nous multiplions par les numérateurs. Ne multipliez pas les dénominateurs car nous voulons pouvoir annuler le facteur$(x−1)$ :

$$=\lim_{x→1}\dfrac{2−(x+1)}{2(x−1)(x+1)}.\nonumber$$

Étape 3 Ensuite, nous simplifions le numérateur :

$$=\lim_{x→1}\dfrac{−x+1}{2(x−1)(x+1)}.\nonumber$$

Étape 4. Maintenant, nous déduisons −1 du numérateur :

$$=\lim_{x→1}\dfrac{−(x−1)}{2(x−1)(x+1)}.\nonumber$$

Étape 5. Ensuite, nous annulons les facteurs communs$(x−1)$ suivants :

$$=\lim_{x→1}\dfrac{−1}{2(x+1)}.\nonumber$$

Étape 6. Enfin, nous évaluons en utilisant les lois limites :

$$\lim_{x→1}\dfrac{−1}{2(x+1)}=−\dfrac{1}{4}.\nonumber$$

Exercice$\PageIndex{6}$

Évaluer$\displaystyle \lim_{x→−3}\dfrac{\dfrac{1}{x+2}+1}{x+3}$.

Allusion

Suivez les étapes de la stratégie de résolution de problèmes

Réponse

−1

$\PageIndex{7}$L'exemple ne correspond parfaitement à aucun des modèles établis dans les exemples précédents. Cependant, avec un peu de créativité, nous pouvons toujours utiliser ces mêmes techniques.

Exemple$\PageIndex{7}$: Evaluating a Limit When the Limit Laws Do Not Apply

Évaluer$\displaystyle \lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)$.

Solution :

Les deux$1/x$ et$5/x(x−5)$ ne parviennent pas à avoir une limite à zéro. Comme aucune des deux fonctions n'a de limite à zéro, nous ne pouvons pas appliquer la loi de somme pour les limites ; nous devons utiliser une stratégie différente. Dans ce cas, nous trouvons la limite en effectuant une addition puis en appliquant l'une de nos stratégies précédentes. Observez que

$$\dfrac{1}{x}+\dfrac{5}{x(x−5)}=\dfrac{x−5+5}{x(x−5)}=\dfrac{x}{x(x−5)}.\nonumber$$

Ainsi,

$$\lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)=\lim_{x→0}\dfrac{x}{x(x−5)}=\lim_{x→0}\dfrac{1}{x−5}=−\dfrac{1}{5}.\nonumber$$

Exercice$\PageIndex{7}$

Évaluer$\displaystyle \lim_{x→3}\left(\dfrac{1}{x−3}−\dfrac{4}{x^2−2x−3}\right)$.

Allusion

Utilisez la même technique que l'exemple$\PageIndex{7}$. N'oubliez pas de prendre en compte$x^2−2x−3$ avant d'obtenir un dénominateur commun.

Réponse

$\dfrac{1}{4}$

Revoyons maintenant les limites unilatérales. De simples modifications des lois sur les limites nous permettent de les appliquer à des limites unilatérales. Par exemple, pour appliquer les lois de limite à une limite du formulaire$\displaystyle \lim_{x→a^−}h(x)$, nous avons besoin que la fonction$h(x)$ soit définie sur un intervalle ouvert du formulaire$(b,a)$ ; pour une limite du formulaire$\displaystyle \lim_{x→a^+}h(x)$, nous avons besoin que la fonction$h(x)$ soit définie sur un intervalle ouvert du formulaire$(a,c)$. L'exemple$\PageIndex{8A}$ illustre ce point.

Exemple$\PageIndex{8A}$: Evaluating a One-Sided Limit Using the Limit Laws

Évaluez chacune des limites suivantes, si possible.

1. $\displaystyle \lim_{x→3^−}\sqrt{x−3}$
2. $\displaystyle \lim_{x→3^+}\sqrt{x−3}$

Solution

La figure$\PageIndex{2}$ illustre la fonction$f(x)=\sqrt{x−3}$ et nous aide à comprendre ces limites.

Figure$\PageIndex{2}$ : Le graphique montre la fonction$f(x)=\sqrt{x−3}$.

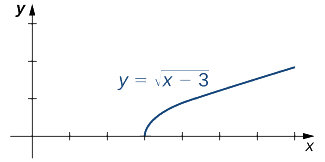
a. La fonction$f(x)=\sqrt{x−3}$ est définie sur l'intervalle$[3,+∞)$. Comme cette fonction n'est pas définie à gauche de 3, nous ne pouvons pas appliquer les lois limites au calcul$\displaystyle\lim_{x→3^−}\sqrt{x−3}$. En fait, puisque n'$f(x)=\sqrt{x−3}$est pas défini à gauche de 3,$\displaystyle\lim_{x→3^−}\sqrt{x−3}$ n'existe pas.

b. Comme il$f(x)=\sqrt{x−3}$ est défini à droite du chiffre 3, les lois limites s'appliquent à$\displaystyle\lim_{x→3^+}\sqrt{x−3}$. En appliquant ces lois limites, nous obtenons$\displaystyle\lim_{x→3^+}\sqrt{x−3}=0$.

Dans Exemple,$\PageIndex{8B}$ nous examinons les limites unilatérales d'une fonction définie par morceaux et utilisons ces limites pour tirer une conclusion sur une limite bilatérale de la même fonction.

Exemple$\PageIndex{8B}$: Evaluating a Two-Sided Limit Using the Limit Laws

Pour$f(x)=\begin{cases}4x−3, & \mathrm{if} \; x<2 \\ (x−3)^2, & \mathrm{if} \; x≥2\end{cases}$, évaluez chacune des limites suivantes :

1. $\displaystyle \lim_{x→2^−}f(x)$
2. $\displaystyle \lim_{x→2^+}f(x)$
3. $\displaystyle \lim_{x→2}f(x)$

Solution

La figure$\PageIndex{3}$ illustre la fonction$f(x)$ et nous aide à comprendre ces limites.

=2, avec l'équation (x-3) ^2. Il y a un cercle fermé en (2,1). Le sommet de la parabole est à (3,0)." src="https://math.libretexts.org/@api/dek...2351/2.3.2.png">

Figure$\PageIndex{3}$ : Ce graphique montre une fonction$f(x)$.

a. Puisque$f(x)=4x−3$ pour tout$x$ entrer$(−∞,2)$, remplacez$f(x)$ la limite par$4x−3$ et appliquez les lois limites :

$$\lim_{x→2^−}f(x)=\lim_{x→2^−}(4x−3)=5\nonumber$$

b. Puisque$f(x)=(x−3)^2$ pour tout$x$ entrer$(2,+∞)$, remplacez$f(x)$ dans la limite$(x−3)^2$ et appliquez les lois limites :

$$\lim_{x→2^+}f(x)=\lim_{x→2^−}(x−3)^2=1. \nonumber$$

c. Depuis$\displaystyle \lim_{x→2^−}f(x)=5$ et$\displaystyle \lim_{x→2^+}f(x)=1$, nous concluons que cela$\displaystyle \lim_{x→2}f(x)$ n'existe pas.

Exercice$\PageIndex{8}$

Tracez$f(x)=\begin{cases}−x−2, & \mathrm{if} \; x<−1\\ 2, & \mathrm{if} \; x=−1 \\ x^3, & \mathrm{if} \; x>−1\end{cases}$ et évaluez$\displaystyle \lim_{x→−1^−}f(x)$.

Allusion

Utilisez la méthode décrite dans Exemple$\PageIndex{8B}$ pour évaluer la limite.

Réponse

-1, qui a croisé les axes x et y à l'origine." src="https://math.libretexts.org/@api/dek...02_03_004.jpeg">

$$\lim_{x→−1^−}f(x)=−1\nonumber$$

Nous nous concentrons maintenant sur l'évaluation d'une limite de la forme$\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}$, où$\displaystyle \lim_{x→a}f(x)=K$, où$K≠0$ et$\displaystyle \lim_{x→a}g(x)=0$. C'est-à-dire,$f(x)/g(x)$ a le formulaire$K/0,K≠0$ à$a$.

Exemple$\PageIndex{9}$: Evaluating a Limit of the Form $K/0,\,K≠0$ Using the Limit Laws

Évaluer$\displaystyle \lim_{x→2^−}\dfrac{x−3}{x^2−2x}$.

Solution

Étape 1 Après la substitution$x=2$, nous voyons que cette limite a la forme$−1/0$. C'est-à-dire qu'$2$à mesure que l'on$x$ s'approche par la gauche, le numérateur s'approche$−1$ ; et le dénominateur s'approche$0$. Par conséquent, l'ampleur de$\dfrac{x−3}{x(x−2)}$ devient infinie. Pour avoir une meilleure idée de la limite, nous devons factoriser le dénominateur :

$$\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=\lim_{x→2^−}\dfrac{x−3}{x(x−2)} \nonumber$$

Étape 2 Puisque$x−2$ c'est la seule partie du dénominateur qui est nulle lorsque 2 est substitué, nous la séparons ensuite$1/(x−2)$ du reste de la fonction :

$$=\lim_{x→2^−}\dfrac{x−3}{x}⋅\dfrac{1}{x−2} \nonumber$$

Étape 3 En utilisant les lois limites, nous pouvons écrire :

$$=\left(\lim_{x→2^−}\dfrac{x−3}{x}\right)\cdot\left(\lim_{x→2^−}\dfrac{1}{x−2}\right). \nonumber$$

Étape 4. $\displaystyle \lim_{x→2^−}\dfrac{x−3}{x}=−\dfrac{1}{2}$et$\displaystyle \lim_{x→2^−}\dfrac{1}{x−2}=−∞$. Par conséquent, le produit de$(x−3)/x$ et$1/(x−2)$ a une limite de$+∞$ :

$$\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=+∞. \nonumber$$

Exercice$\PageIndex{9}$

Évaluer$\displaystyle \lim_{x→1}\dfrac{x+2}{(x−1)^2}$.

Solution

Utilisez les méthodes de l'exemple$\PageIndex{9}$.

Réponse

$+∞$

Le théorème de la compression

Les techniques que nous avons développées jusqu'à présent fonctionnent très bien pour les fonctions algébriques, mais nous ne sommes toujours pas en mesure d'évaluer les limites de fonctions trigonométriques très basiques. Le théorème suivant, appelé théorème de compression, s'avère très utile pour établir les limites trigonométriques de base. Ce théorème nous permet de calculer des limites en « comprimant » une fonction, avec une limite à un point$a$ inconnu, entre deux fonctions ayant une limite connue commune à$a$. La figure$\PageIndex{4}$ illustre cette idée.

Figure$\PageIndex{4}$ : Le théorème de compression s'applique quand$f(x)≤g(x)≤h(x)$ et$\displaystyle \lim_{x→a}f(x)=\lim_{x→a}h(x)$.

Le théorème de la compression

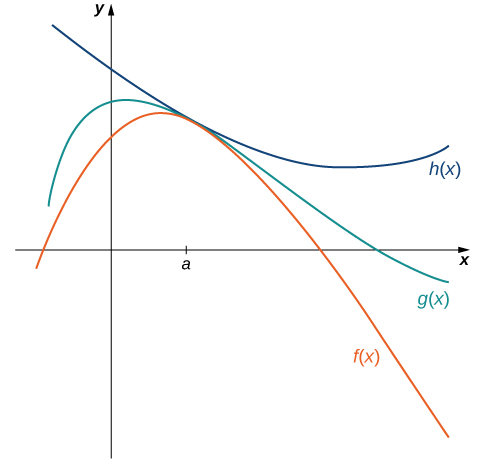
Soit$f(x),g(x)$, et$h(x)$ être défini pour tout$x≠a$ sur un intervalle ouvert contenant$a$. Si

$$f(x)≤g(x)≤h(x) \nonumber$$

pour tous$x≠a$ dans un intervalle ouvert contenant$a$ et

$$\lim_{x→a}f(x)=L=\lim_{x→a}h(x) \nonumber$$

où$L$ est un nombre réel, alors$\displaystyle \lim_{x→a}g(x)=L.$

Exemple$\PageIndex{10}$: Applying the Squeeze Theorem

Appliquez le théorème de compression pour évaluer$\displaystyle \lim_{x→0} x \cos x$.

Solution

Parce que$−1≤\cos x≤1$ pour tous$x$, nous avons$−x≤x \cos x≤x$ pour$x≥0$ et$−x≥x \cos x ≥ x$ pour$x≤0$ (si$x$ c'est négatif, la direction des inégalités change lorsque nous nous multiplions). Puisque$\displaystyle \lim_{x→0}(−x)=0=\lim_{x→0}x$, à partir du théorème de compression, on obtient$\displaystyle \lim_{x→0}x \cos x=0$. Les graphiques de$f(x)=−x,\;g(x)=x\cos x$ et$h(x)=x$ sont présentés sur la figure$\PageIndex{5}$.

0 et vers le bas pour x>0." src="https://math.libretexts.org/@api/dek...2350/2.3.3.png">

Figure$\PageIndex{5}$ : Les graphiques$f(x),\,g(x)$ de et$h(x)$ sont présentés autour du point$x=0$.

Exercice$\PageIndex{10}$

Utilisez le théorème de compression pour évaluer$\displaystyle \lim_{x→0}x^2 \sin\dfrac{1}{x}$.

Allusion

Utilisez le fait que$−x^2≤x^2\sin (1/x) ≤ x^2$ pour vous aider à trouver deux fonctions qui$x^2\sin (1/x)$ sont placées entre elles.

Réponse

0

Nous utilisons maintenant le théorème de compression pour aborder plusieurs limites très importantes. Bien que cette discussion soit assez longue, ces limites s'avèrent inestimables pour le développement du matériel de la section suivante et du chapitre suivant. La première de ces limites est$\displaystyle \lim_{θ→0}\sin θ$. Considérez le cercle unitaire illustré sur la figure$\PageIndex{6}$. Sur la figure, nous voyons qu'il$\sin θ$ s'agit de la$y$ coordonnée -sur le cercle unitaire et qu'elle correspond au segment de ligne indiqué en bleu. La mesure en radian de l'angle$θ$ est la longueur de l'arc qu'elle sous-tend sur l'unité de cercle. Par conséquent, nous constatons que$0<θ<\dfrac{π}{2},$ nous avons$0<\sin θ<θ.$

Figure$\PageIndex{6}$ : La fonction sinusoïdale est représentée par une ligne sur le cercle unitaire.

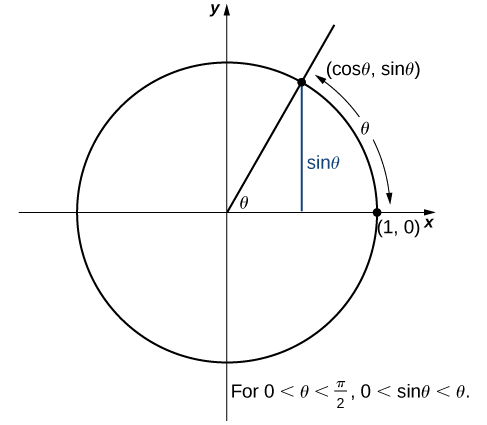
Parce que$\displaystyle \lim_{θ→0^+}0=0$ et$\displaystyle \lim_{x→0^+}θ=0$, en utilisant le théorème de compression, nous concluons que

$$\lim_{θ→0^+}\sin θ=0.\nonumber$$

Pour voir cela$\displaystyle \lim_{θ→0^−}\sin θ=0$ aussi, observez cela pour$−\dfrac{π}{2}<θ<0,0<−θ<\dfrac{π}{2}$ et donc,$0<\sin(−θ)<−θ$. Par conséquent,$0<−\sin θ<−θ$. Il s'ensuit que$0>\sin θ>θ$. L'application du théorème de compression produit la limite souhaitée. Ainsi, depuis$\displaystyle \lim_{θ→0^+}\sin θ=0$ et$\displaystyle \lim_{θ→0^−}\sin θ=0$,

$$\lim_{θ→0}\sin θ=0\nonumber$$

Ensuite, en utilisant l'identité$\cos θ=\sqrt{1−\sin^2θ}$ pour$−\dfrac{π}{2}<θ<\dfrac{π}{2}$, nous voyons que

$$\lim_{θ→0}\cos θ=\lim_{θ→0}\sqrt{1−\sin^2θ}=1.\nonumber$$

Nous examinons maintenant une limite qui joue un rôle important dans les chapitres suivants, à savoir,$\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}$. Pour évaluer cette limite, nous utilisons le cercle unitaire de la figure$\PageIndex{7}$. Notez que cette figure ajoute un triangle supplémentaire à la figure$\PageIndex{6}$. Nous voyons que la longueur de l'angle opposé$θ$ dans ce nouveau triangle est de$\tan θ$. Ainsi, nous voyons que pour$0<θ<\dfrac{π}{2}$, nous l'avons fait$\sin θ<θ<\tanθ$.

Figure$\PageIndex{7}$ : Les fonctions sinusoïdale et tangente sont affichées sous forme de lignes sur le cercle unitaire.

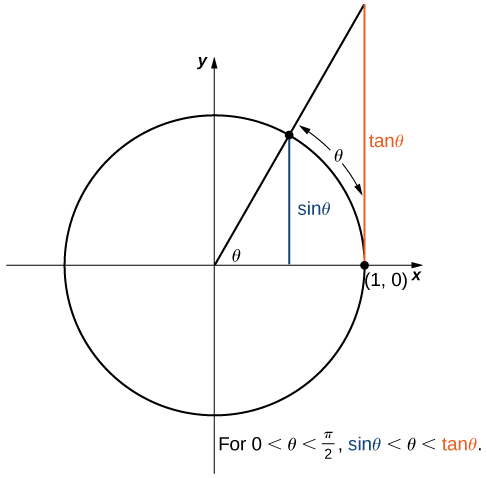
En divisant par$\sin θ$ toutes les parties de l'inégalité, nous obtenons

$$1<\dfrac{θ}{\sin θ}<\dfrac{1}{\cos θ}.\nonumber$$

De manière équivalente, nous avons

$$1>\dfrac{\sin θ}{θ}>\cos θ.\nonumber$$

Puisque$\displaystyle \lim_{θ→0^+}1=1=\lim_{θ→0^+}\cos θ$, nous en concluons$\displaystyle \lim_{θ→0^+}\dfrac{\sin θ}{θ}=1$, par le théorème de compression. En appliquant une manipulation similaire à celle utilisée pour le démontrer$\displaystyle \lim_{θ→0^−}\sin θ=0$, nous pouvons le démontrer$\displaystyle \lim_{θ→0^−}\dfrac{\sin θ}{θ}=1$. Ainsi,

$$\lim_{θ→0}\dfrac{\sin θ}{θ}=1. \nonumber$$

Dans l'exemple$\PageIndex{11}$, nous utilisons cette limite pour établir$\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0$. Cette limite s'avère également utile dans les chapitres suivants.

Exemple$\PageIndex{11}$: Evaluating an Important Trigonometric Limit

Évaluer$\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}$.

Solution

Dans un premier temps, nous multiplions par le conjugué afin de pouvoir utiliser une identité trigonométrique pour convertir le cosinus du numérateur en sinus :

\ [\ begin {align*} \ lim_ {θ→0} \ dfrac {1− \ cos θ} {θ} &= \ displaystyle \ lim_ {θ→0} \ dfrac {1− \ cos θ} {θ} ⋅ \ dfrac {1+ \ cos θ} {1+ \ cos θ} \ \ [4 points]
&= \ lim_ {θ→0} \ dfrac {1+ \ cos θ} \ \ [4 points] &= \ lim_ {θ→0} \ dfrac ac {1− \ cos^2θ} {θ (1+ \ cos θ)} \ \ [4 points]
&= \ lim_ {θ→0} \ dfrac {\ sin^2θ} {θ (1+ \ cos θ)} \ \ [4 points]
&= \ lim_ {θ→0} \ dfrac {\ sin θ } {θ} ⋅ \ dfrac {\ sin θ} {1+ \ cos θ} \ \ [4pt]
&= \ left (\ lim_ {θ→0} \ dfrac {\ sin θ} {θ} \ droite) \ cdot \ left (\ lim_ {θ→0} \ dfrac {\ sin θ} {1+ \ cos θ} \ droite) \ \ [4pt]
&= 1⋅ \ frac {0} {2} =0. \ end {align*} \]

Par conséquent,

$$\lim_{θ→0}\dfrac{1−\cos θ}{θ}=0. \nonumber$$

Exercice$\PageIndex{11}$

Évaluer$\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{\sin θ}$.

Allusion

Multipliez le numérateur et le dénominateur par$1+\cos θ$.

Réponse

0

Dériver la formule pour l'aire d'un cercle

Certaines des formules géométriques que nous tenons pour acquises aujourd'hui ont d'abord été dérivées par des méthodes qui anticipent certaines méthodes de calcul. Le mathématicien grec Archimède (env. 287−212 ; av. J.-C.) était particulièrement inventif, utilisant des polygones inscrits dans des cercles pour approximer l'aire du cercle à mesure que le nombre de côtés du polygone augmentait. Il n'a jamais eu l'idée d'une limite, mais nous pouvons utiliser cette idée pour voir ce que ses constructions géométriques auraient pu prédire à propos de la limite.

Nous pouvons estimer l'aire d'un cercle en calculant l'aire d'un polygone régulier inscrit. Imaginez que le polygone régulier est composé de$n$ triangles. En prenant la limite lorsque l'angle des sommets de ces triangles passe à zéro, vous pouvez obtenir l'aire du cercle. Pour ce faire, procédez comme suit :

1. Exprimez la hauteur$h$ et la base$b$ du triangle isocèle de la figure$\PageIndex{8}$ en termes$θ$ et$r$.

Figurine$\PageIndex{8}$

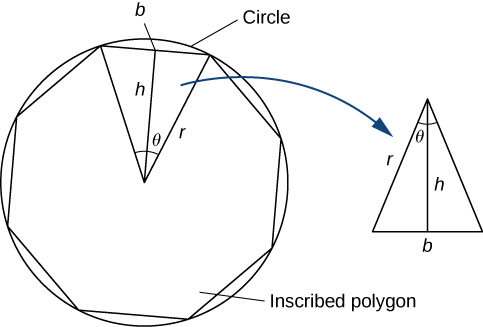
2. À l'aide des expressions que vous avez obtenues à l'étape 1, exprimez l'aire du triangle isocèle en termes de$θ$ et$r$.

(Substitut$\frac{1}{2}\sin θ$ de$\sin\left(\frac{θ}{2}\right)\cos\left(\frac{θ}{2}\right)$ dans votre expression.)

3. Si un polygone régulier à$n$ côtés est inscrit dans un cercle de rayon$r$, trouvez une relation entre$θ$ et$n$. Résolvez ce problème pour$n$. Gardez à l'esprit qu'il y a$2π$ des radians dans un cercle. (Utilisez des radians et non des degrés.)

4. Trouvez une expression pour l'aire du$n$ polygone latéral en termes de$r$ et$θ$.

5. Pour trouver une formule pour l'aire du cercle, déterminez la limite de l'expression à l'étape 4$θ$ jusqu'à zéro. (Astuce :$\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}=1)$.

La technique d'estimation des superficies de régions à l'aide de polygones est revue dans Introduction à l'intégration.

Concepts clés

• Les lois de limites nous permettent d'évaluer les limites des fonctions sans avoir à passer par des processus étape par étape à chaque fois.
• Pour les polynômes et les fonctions rationnelles, $$\lim_{x→a}f(x)=f(a). \nonumber$$
• Vous pouvez évaluer la limite d'une fonction en factorisant et en annulant, en multipliant par un conjugué ou en simplifiant une fraction complexe.
• Le théorème de compression permet de déterminer la limite d'une fonction si celle-ci est toujours supérieure à une fonction et inférieure à une autre fonction dont les limites sont connues.

Équations clés

• Résultats limites de base

$$\lim_{x→a}x=a \quad \quad \lim_{x→a}c=c \nonumber$$

• Limites importantes

$$\lim_{θ→0}\sin θ=0 \nonumber$$

$$\lim_{θ→0}\cos θ=1 \nonumber$$

$$\lim_{θ→0}\dfrac{\sin θ}{θ}=1 \nonumber$$

$$\lim_{θ→0}\dfrac{1−\cos θ}{θ}=0 \nonumber$$

Lexique

loi multiple constante pour les limites

la loi limite $$\lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber$$

loi de différence pour les limites

la loi limite $$\lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M\nonumber$$

lois sur les limites

les propriétés individuelles des limites ; pour chacune des lois individuelles,$g(x)$ soit définie pour l'ensemble$x≠a$ sur un intervalle ouvert contenant a ; supposons que L et M sont des nombres réels, de sorte que$\lim_{x→a}f(x)=L$ et$\lim_{x→a}g(x)=M$ ; soit c une constante$f(x)$

loi sur la puissance pour les limites

la loi limite $$\lim_{x→a}(f(x))^n=(\lim_{x→a}f(x))^n=L^n\nonumber$$ pour chaque entier positif n

droit des produits en matière de limites

la loi limite $$\lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M\nonumber$$

loi du quotient pour les limites

la loi limite$\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{\lim_{x→a}f(x)}{\lim_{x→a}g(x)}=\dfrac{L}{M}$ pour M≥0

loi fondamentale pour les limites

la loi limite$\lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a}f(x)}=\sqrt[n]{L}$ pour tous les L si n est impair et pour$L≥0$ si n est pair

théorème de compression

indique que si$f(x)≤g(x)≤h(x)$ pour tout un$x≠a$ intervalle ouvert contenant a et$\lim_{x→a}f(x)=L=\lim_ {x→a}h(x)$ où L est un nombre réel, alors$\lim_{x→a}g(x)=L$

loi de somme pour les limites

La loi des limites$\lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M$